Los modelos de aprendizaje automático se eligen en función de su rendimiento medio, a menudo calculado mediante una validación cruzada de k.
Se espera que el algoritmo con el mejor rendimiento medio sea mejor que los algoritmos con peor rendimiento medio. ¿Pero qué pasa si la diferencia en el rendimiento medio es causada por una casualidad estadística?
La solución es utilizar un prueba de hipótesis estadística para evaluar si la diferencia en el rendimiento medio entre dos algoritmos cualquiera es real o no.
En este tutorial, descubrirá cómo utilizar las pruebas de hipótesis estadísticas para comparar los algoritmos de aprendizaje automático.
Después de completar este tutorial, lo sabrás:
- Realizar una selección de modelos basada en el rendimiento medio de los modelos puede ser engañoso.
- Las cinco repeticiones de la validación cruzada doble con un test t modificado de Student es una buena práctica para comparar los algoritmos de aprendizaje de las máquinas.
- Cómo usar la máquina MLxtend aprendiendo a comparar algoritmos usando una prueba de hipótesis estadística.
Ponga en marcha su proyecto con mi nuevo libro «Statistics for Machine Learning», que incluye tutoriales paso a paso y el El código fuente de Python archivos para todos los ejemplos.
Empecemos.

Prueba de hipótesis para comparar los algoritmos de aprendizaje automático
Foto de Frank Shepherd, algunos derechos reservados.
Resumen del Tutorial
Este tutorial está dividido en tres partes; son:
- Prueba de hipótesis para comparar algoritmos
- Procedimiento 5×2 con MLxtend
- Comparación de los algoritmos de clasificación
Prueba de hipótesis para comparar algoritmos
La selección del modelo implica la evaluación de un conjunto de diferentes algoritmos de aprendizaje de máquinas o de modelización de tuberías y su comparación en función de su rendimiento.
El modelo o tubería de modelación que logra el mejor desempeño de acuerdo con su métrica de desempeño es entonces seleccionado como su modelo final que puede utilizar para comenzar a hacer predicciones sobre nuevos datos.
Esto se aplica a las tareas de modelado predictivo de regresión y clasificación con algoritmos clásicos de aprendizaje de máquinas y aprendizaje profundo. Siempre es el mismo proceso.
El problema es, ¿cómo sabes que la diferencia entre dos modelos es real y no sólo una casualidad estadística?
Este problema puede abordarse mediante una prueba de hipótesis estadística.
Un enfoque consiste en evaluar cada modelo en la misma división de validación cruzada de los datos (por ejemplo, utilizando la misma semilla de números aleatorios para dividir los datos en cada caso) y calcular una puntuación para cada división. Esto daría una muestra de 10 puntuaciones para una validación cruzada de 10 veces. Las puntuaciones pueden entonces compararse utilizando una prueba de hipótesis estadísticas emparejadas porque se utilizó el mismo tratamiento (filas de datos) para cada algoritmo para obtener cada puntuación. Se puede utilizar la prueba t de estudiantes emparejados.
El problema de usar el test t de estudiantes emparejados, en este caso, es que cada evaluación del modelo no es independiente. Esto se debe a que las mismas filas de datos se utilizan para entrenar los datos varias veces – en realidad, cada vez, excepto por el tiempo que una fila de datos se utiliza en el pliegue de la prueba de retención. Esta falta de independencia en la evaluación significa que la prueba t del estudiante emparejado está sesgada de forma optimista.
Esta prueba estadística puede ajustarse para tener en cuenta la falta de independencia. Además, el número de pliegues y repeticiones del procedimiento puede configurarse para lograr un buen muestreo del rendimiento del modelo que generalice bien a una amplia gama de problemas y algoritmos. En concreto, la validación cruzada de dos pliegues con cinco repeticiones, la llamada validación cruzada de 5×2 pliegues.
Este enfoque fue propuesto por Thomas Dietterich en su documento de 1998 titulado «Pruebas estadísticas aproximadas para comparar los algoritmos de aprendizaje de clasificación supervisada».
Para obtener más información sobre este tema, consulte el tutorial:
Afortunadamente, no necesitamos implementar este procedimiento nosotros mismos.
Procedimiento 5×2 con MLxtend
La biblioteca MLxtend de Sebastian Raschka proporciona una implementación a través de la paired_ttest_5x2cv() función.
Primero, debe instalar la biblioteca mlxtend, por ejemplo:
Para utilizar la evaluación, primero debe cargar su conjunto de datos, y luego definir los dos modelos que desea comparar.
|
... # Cargar datos X, y = .... # Definir los modelos modelo1 = ... modelo2 = ... |
Entonces puedes llamar al paired_ttest_5x2cv() y pasará en sus datos y modelos y reportará el valor t-estadístico y el valor p en cuanto a si la diferencia en el rendimiento de los dos algoritmos es significativa o no.
|
... # Comparar algoritmos t, p = paired_ttest_5x2cv(estimador1=modelo1, estimador2=modelo2, X=X, y=y) |
El valor p debe ser interpretado usando un valor alfa, que es el nivel de significación que está dispuesto a aceptar.
Si el valor p es menor o igual que el alfa elegido, rechazamos la hipótesis nula de que los modelos tengan el mismo rendimiento medio, lo que significa que la diferencia es probablemente real. Si el valor p es mayor que el alfa, no rechazamos la hipótesis nula de que los modelos tienen el mismo rendimiento medio y cualquier diferencia observada en las precisiones medias es probablemente una casualidad estadística.
Cuanto más pequeño sea el valor alfa, mejor, y un valor común es el 5 por ciento (0,05).
|
... # Interpretar el resultado si p <= 0.05: imprimir(«La diferencia entre el rendimiento medio es probablemente real) más: imprimir(Los algoritmos probablemente tienen el mismo rendimiento.) |
Ahora que estamos familiarizados con la forma de usar una prueba de hipótesis para comparar algoritmos, veamos algunos ejemplos.
Comparación de los algoritmos de clasificación
En esta sección, vamos a comparar el rendimiento de dos algoritmos de aprendizaje automático en una tarea de clasificación binaria, y luego comprobar si la diferencia observada es estadísticamente significativa o no.
Primero, podemos usar la función make_classification() para crear un conjunto de datos sintéticos con 1.000 muestras y 20 variables de entrada.
El ejemplo siguiente crea el conjunto de datos y resume su forma.
|
# Crear un conjunto de datos de clasificación de sklearn.conjuntos de datos importación hacer_clasificación # Definir el conjunto de datos X, y = make_classification(n_muestras=1000, n_funciones=10, n_informativo=10, n_redundante=0, estado_aleatorio=1) # resumir el conjunto de datos imprimir(X.forma, y.forma) |
Ejecutando el ejemplo se crea el conjunto de datos y se resume el número de filas y columnas, confirmando nuestras expectativas.
Podemos usar estos datos como base para comparar dos algoritmos.
Compararemos el rendimiento de dos algoritmos lineales en este conjunto de datos. Específicamente, un algoritmo de regresión logística y un algoritmo de análisis discriminante lineal (LDA).
El procedimiento que me gusta es usar la validación cruzada estratificada k con 10 pliegues y tres repeticiones. Usaremos este procedimiento para evaluar cada algoritmo y devolver y reportar la precisión de la clasificación media.
El ejemplo completo figura a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
# Compara la regresión logística y la IDA para la clasificación binaria de numpy importación significa de numpy importación std de sklearn.conjuntos de datos importación make_classification de sklearn.model_selection importación puntaje_valor_cruzado de sklearn.model_selection importación RepeatedStratifiedKFold de sklearn.modelo_lineal importación LogisticRegression de sklearn.análisis_discriminatorio importación LinearDiscriminantAnalysis de matplotlib importación pyplot # Definir el conjunto de datos X, y = make_classification(n_muestras=1000, n_funciones=10, n_informativo=10, n_redundante=0, estado_aleatorio=1) # Evaluar el modelo 1 modelo1 = LogisticRegression() cv1 = RepeatedStratifiedKFold(n_splits=10, n_repeticiones=3, estado_aleatorio=1) resultados1 = puntaje_valor_cruzado(modelo1, X, y, puntuación=«exactitud, cv=cv1, n_jobs=–1) imprimir(«Exactitud media de la regresión logística: %.3f (%.3f) % (significa(resultados1), std(resultados1))) # Evaluar el modelo 2 modelo2 = LinearDiscriminantAnalysis() cv2 = RepeatedStratifiedKFold(n_splits=10, n_repeticiones=3, estado_aleatorio=1) puntuaciones2 = puntaje_valor_cruzado(modelo2, X, y, puntuación=«exactitud, cv=cv2, n_jobs=–1) imprimir(«Exactitud media del análisis discriminante lineal: %.3f (%.3f) % (significa(puntuaciones2), std(puntuaciones2))) # trazar los resultados pyplot.Boxplot([[resultados1, puntuaciones2], etiquetas=[[LR, LDA], showmeans=Verdadero) pyplot.mostrar() |
Ejecutando el ejemplo primero se informa de la precisión de la clasificación media para cada algoritmo.
Sus resultados específicos pueden diferir dada la naturaleza estocástica de los algoritmos de aprendizaje y el procedimiento de evaluación. Intente ejecutar el ejemplo unas cuantas veces.
En este caso, los resultados sugieren que el LDA tiene un mejor rendimiento si sólo miramos las puntuaciones medias: 89,2 por ciento para la regresión logística y 89,3 por ciento para el LDA.
|
Exactitud media de la regresión logística: 0,892 (0,036) Exactitud media del análisis discriminante lineal: 0,893 (0,033) |
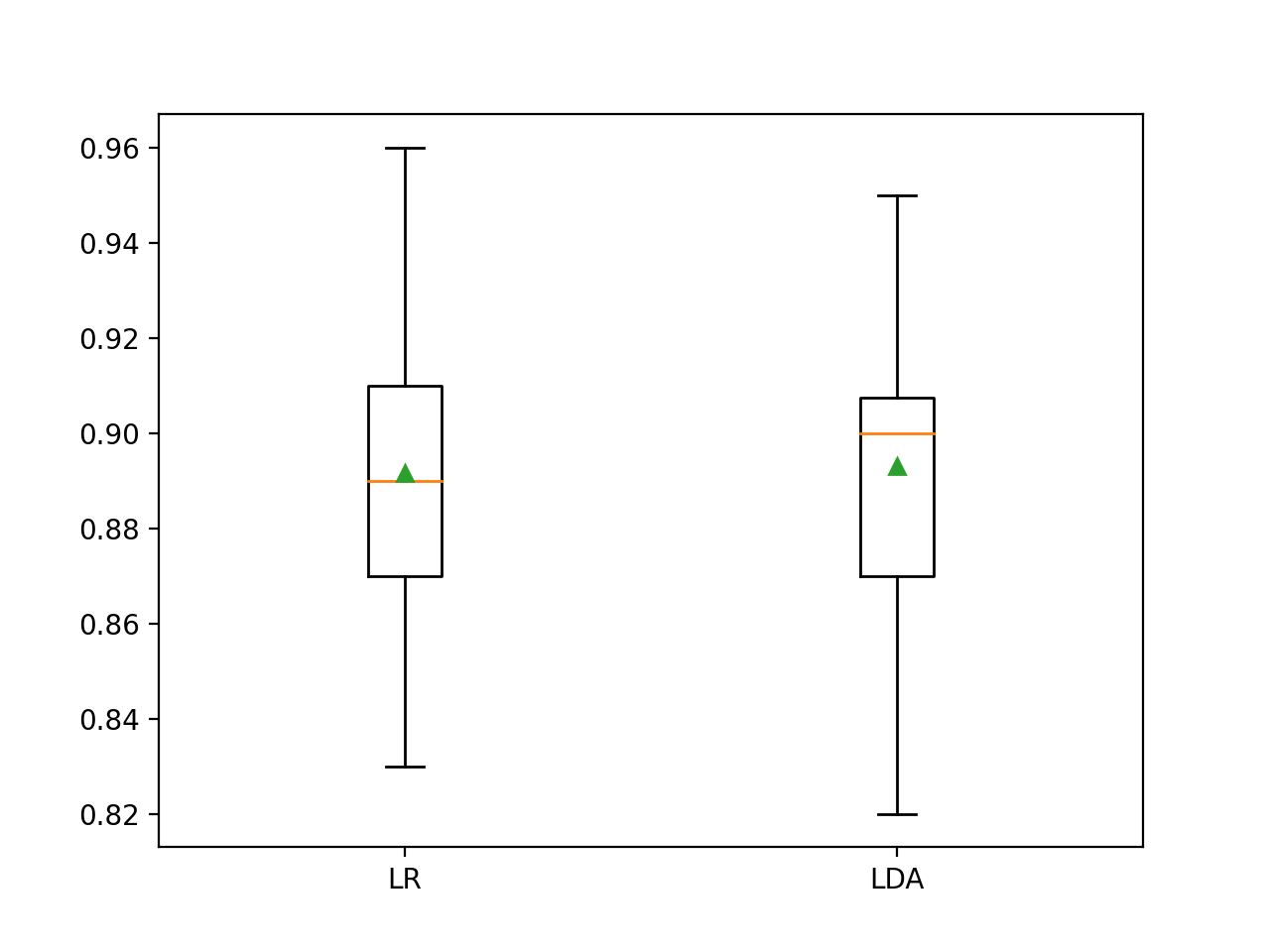
También se crea un gráfico de caja y bigote que resume la distribución de las puntuaciones de precisión.
Este complot apoyaría mi decisión de elegir a LDA en lugar de LR.

Cuadro y diagrama de bigote de las puntuaciones de precisión de clasificación para dos algoritmos
Ahora podemos usar una prueba de hipótesis para ver si los resultados observados son estadísticamente significativos.
Primero, usaremos el procedimiento 5×2 para evaluar los algoritmos y calcular un valor p y un valor estadístico de prueba.
|
... # Comprueba si la diferencia entre los algoritmos es real t, p = paired_ttest_5x2cv(estimador1=modelo1, estimador2=modelo2, X=X, y=y, puntuación=«exactitud, random_seed=1) # Resumir imprimir(«Valor P: %.3f, t-estadístico: %.3f % (p, t)) |
Podemos entonces interpretar el valor p usando un alfa del 5 por ciento.
|
... # Interpretar el resultado si p <= 0.05: imprimir(«La diferencia entre el rendimiento medio es probablemente real) más: imprimir(Los algoritmos probablemente tienen el mismo rendimiento.) |
A continuación se muestra el ejemplo completo.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
# Usar el procedimiento de prueba de hipótesis estadísticas 5×2 para comparar dos algoritmos de aprendizaje automático de numpy importación significa de numpy importación std de sklearn.conjuntos de datos importación make_classification de sklearn.model_selection importación puntaje_valor_cruzado de sklearn.model_selection importación RepeatedStratifiedKFold de sklearn.modelo_lineal importación LogisticRegression de sklearn.análisis_discriminatorio importación LinearDiscriminantAnalysis de mlxtend.evalúa importación paired_ttest_5x2cv # Definir el conjunto de datos X, y = make_classification(n_muestras=1000, n_funciones=10, n_informativo=10, n_redundante=0, estado_aleatorio=1) # Evaluar el modelo 1 modelo1 = LogisticRegression() cv1 = RepeatedStratifiedKFold(n_splits=10, n_repeticiones=3, estado_aleatorio=1) resultados1 = puntaje_valor_cruzado(modelo1, X, y, puntuación=«exactitud, cv=cv1, n_jobs=–1) imprimir(«Exactitud media de la regresión logística: %.3f (%.3f) % (significa(resultados1), std(resultados1))) # Evaluar el modelo 2 modelo2 = LinearDiscriminantAnalysis() cv2 = RepeatedStratifiedKFold(n_splits=10, n_repeticiones=3, estado_aleatorio=1) puntuaciones2 = puntaje_valor_cruzado(modelo2, X, y, puntuación=«exactitud, cv=cv2, n_jobs=–1) imprimir(«Exactitud media del análisis discriminante lineal: %.3f (%.3f) % (significa(puntuaciones2), std(puntuaciones2))) # Comprueba si la diferencia entre los algoritmos es real t, p = paired_ttest_5x2cv(estimador1=modelo1, estimador2=modelo2, X=X, y=y, puntuación=«exactitud, random_seed=1) # Resumir imprimir(«Valor P: %.3f, t-estadístico: %.3f % (p, t)) # Interpretar el resultado si p <= 0.05: imprimir(«La diferencia entre el rendimiento medio es probablemente real) más: imprimir(Los algoritmos probablemente tienen el mismo rendimiento.) |
Ejecutando el ejemplo, primero evaluamos los algoritmos antes, y luego informamos sobre el resultado de la prueba de hipótesis estadística.
Sus resultados específicos pueden diferir dada la naturaleza estocástica de los algoritmos de aprendizaje y el procedimiento de evaluación. Intente ejecutar el ejemplo unas cuantas veces.
En este caso, podemos ver que el valor p es de aproximadamente 0,3, que es mucho mayor que 0,05. Esto nos lleva a no rechazar la hipótesis nula, sugiriendo que cualquier diferencia observada entre los algoritmos probablemente no es real.
Podríamos elegir fácilmente la regresión logística o el LDA y ambos tendrían el mismo rendimiento en promedio.
Esto pone de relieve que realizar una selección de modelos basada sólo en el rendimiento medio puede no ser suficiente.
|
Exactitud media de la regresión logística: 0,892 (0,036) Exactitud media del análisis discriminante lineal: 0,893 (0,033) Valor P: 0,328, t-estadístico: 1,085 Los algoritmos probablemente tienen el mismo rendimiento |
Recordemos que estamos reportando el rendimiento usando un procedimiento diferente (3×10 CV) que el procedimiento usado para estimar el rendimiento en la prueba estadística (5×2 CV). ¿Quizás los resultados serían diferentes si miráramos las puntuaciones usando cinco repeticiones de validación cruzada doble?
El ejemplo que figura a continuación se actualiza para informar de la exactitud de la clasificación de cada algoritmo utilizando 5×2 CV.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
# Usar el procedimiento de prueba de hipótesis estadísticas 5×2 para comparar dos algoritmos de aprendizaje automático de numpy importación significa de numpy importación std de sklearn.conjuntos de datos importación make_classification de sklearn.model_selection importación puntaje_valor_cruzado de sklearn.model_selection importación RepeatedStratifiedKFold de sklearn.modelo_lineal importación LogisticRegression de sklearn.análisis_discriminatorio importación LinearDiscriminantAnalysis de mlxtend.evalúa importación paired_ttest_5x2cv # Definir el conjunto de datos X, y = make_classification(n_muestras=1000, n_funciones=10, n_informativo=10, n_redundante=0, estado_aleatorio=1) # Evaluar el modelo 1 modelo1 = LogisticRegression() cv1 = RepeatedStratifiedKFold(n_splits=2, n_repeticiones=5, estado_aleatorio=1) resultados1 = puntaje_valor_cruzado(modelo1, X, y, puntuación=«exactitud, cv=cv1, n_jobs=–1) imprimir(«Exactitud media de la regresión logística: %.3f (%.3f) % (significa(resultados1), std(resultados1))) # Evaluar el modelo 2 modelo2 = LinearDiscriminantAnalysis() cv2 = RepeatedStratifiedKFold(n_splits=2, n_repeticiones=5, estado_aleatorio=1) puntuaciones2 = puntaje_valor_cruzado(modelo2, X, y, puntuación=«exactitud, cv=cv2, n_jobs=–1) imprimir(«Exactitud media del análisis discriminante lineal: %.3f (%.3f) % (significa(puntuaciones2), std(puntuaciones2))) # Comprueba si la diferencia entre los algoritmos es real t, p = paired_ttest_5x2cv(estimador1=modelo1, estimador2=modelo2, X=X, y=y, puntuación=«exactitud, random_seed=1) # Resumir imprimir(«Valor P: %.3f, t-estadístico: %.3f % (p, t)) # Interpretar el resultado si p <= 0.05: imprimir(«La diferencia entre el rendimiento medio es probablemente real) más: imprimir(Los algoritmos probablemente tienen el mismo rendimiento.) |
La ejecución del ejemplo informa de la precisión media tanto de los algoritmos como de los resultados de la prueba estadística.
Sus resultados específicos pueden diferir dada la naturaleza estocástica de los algoritmos de aprendizaje y el procedimiento de evaluación. Intente ejecutar el ejemplo unas cuantas veces.
En este caso, podemos ver que la diferencia en el rendimiento medio de los dos algoritmos es aún mayor, 89,4 por ciento contra 89,0 por ciento a favor de la regresión logística en lugar de la LDA como vimos con 3×10 CV.
|
Exactitud media de la regresión logística: 0,894 (0,012) Exactitud media del análisis discriminante lineal: 0,890 (0,013) Valor P: 0,328, t-estadístico: 1,085 Los algoritmos probablemente tienen el mismo rendimiento |
