Los conjuntos subespaciales aleatorios consisten en el mismo modelo que se ajusta a diferentes grupos de características de entrada (columnas) seleccionadas al azar en el conjunto de datos de entrenamiento.
Hay muchas maneras de elegir grupos de características en el conjunto de datos de capacitación, y la selección de características es una clase popular de técnicas de preparación de datos diseñadas específicamente para este propósito. Los rasgos seleccionados por diferentes configuraciones del mismo método de selección de rasgos y de diferentes métodos de selección de rasgos pueden utilizarse totalmente como base para el aprendizaje en conjunto.
En este tutorial, descubrirás cómo desarrollar selección de características de los conjuntos subespaciales con Python.
Después de completar este tutorial, lo sabrás:
- La selección de características proporciona una alternativa a los subespacios aleatorios para seleccionar grupos de características de entrada.
- Cómo desarrollar y evaluar conjuntos compuestos por características seleccionadas por técnicas de selección de características únicas.
- Cómo desarrollar y evaluar conjuntos compuestos por características seleccionadas por múltiples técnicas diferentes de selección de características.
Empecemos.

Cómo desarrollar un conjunto subespacial de selección de características en Python
Foto de Bernard Spragg. NZ, algunos derechos reservados.
Resumen del Tutorial
Este tutorial está dividido en tres partes; son:
- Selección de características Conjunto subespacial
- El método de selección de una sola característica se ensambla
- Conjunto F-estadístico ANOVA
- Conjunto de información mutua
- Conjunto de selección de características recursivas
- Conjuntos de selección de características combinadas
- Conjunto con un número fijo de características
- Conjunto con un número contiguo de características
Selección de características Conjunto subespacial
El método subespacial aleatorio o conjunto subespacial aleatorio es un enfoque de aprendizaje en conjunto que se ajusta a un modelo en diferentes grupos de columnas seleccionadas al azar en el conjunto de datos de entrenamiento.
La diferencia en la elección de las columnas utilizadas para entrenar a cada modelo en el conjunto da como resultado una diversidad de modelos y sus predicciones. Cada modelo funciona bien, aunque cada uno actúa de forma diferente, cometiendo diferentes errores.
Los datos de entrenamiento suelen describirse mediante un conjunto de características. Diferentes subconjuntos de características, o llamados subespacios, proporcionan diferentes puntos de vista sobre los datos. Por lo tanto, los alumnos individuales capacitados desde diferentes subespacios suelen ser diversos.
– Página 116, Métodos de ensamblaje, 2012.
El método subespacial aleatorio se utiliza a menudo con árboles de decisión y las predicciones hechas por cada árbol se combinan luego utilizando estadísticas simples, como el cálculo de la etiqueta de clase de modo para la clasificación o la predicción media para la regresión.
La selección de características es una técnica de preparación de datos que intenta seleccionar un subconjunto de columnas en un conjunto de datos que es más relevante para la variable objetivo. Los enfoques más populares implican el uso de medidas estadísticas, como la información mutua, y la evaluación de modelos sobre subconjuntos de características y la selección del subconjunto que da lugar al modelo de mejor rendimiento, denominado eliminación recursiva de características, o RFE para abreviar.
Cada método de selección de características tendrá una idea diferente o una conjetura informada sobre qué características son más relevantes para la variable objetivo. Además, los métodos de selección de características pueden adaptarse para seleccionar un número específico de características desde 1 hasta el número total de columnas del conjunto de datos, un hiperparámetro que puede ajustarse como parte de la selección del modelo.
Cada conjunto de características seleccionadas puede considerarse como un subconjunto del espacio de características de entrada, muy parecido a un conjunto subespacial aleatorio, aunque elegido utilizando una métrica en lugar de al azar. Podemos utilizar características elegidas por métodos de selección de características como un tipo de modelo de conjunto.
Puede haber muchas maneras de ponerlo en práctica, pero tal vez haya dos enfoques naturales:
- Un método: Generar un subespacio de características para cada número de características desde 1 hasta el número de columnas del conjunto de datos, ajustar un modelo en cada una y combinar sus predicciones.
- Múltiples métodos: Generar un subespacio de características usando múltiples métodos de selección de características diferentes, ajustar un modelo en cada una y combinar sus predicciones.
A falta de un nombre mejor, podemos referirnos a esto como «Selección de características Conjunto subespacial.”
Exploraremos esta idea en este tutorial.
Definamos un problema de prueba como la base de esta exploración y establezcamos una línea de base en el rendimiento para ver si ofrece un beneficio sobre un modelo único.
Primero, podemos usar la función make_classification() para crear un problema de clasificación binaria sintética con 1.000 ejemplos y 20 características de entrada, cinco de las cuales son redundantes.
El ejemplo completo figura a continuación.
|
# Conjunto de datos de clasificación sintética de sklearn.conjuntos de datos importación hacer_clasificación # Definir el conjunto de datos X, y = make_classification(n_muestras=1000, n_funciones=20, n_informativo=15, n_redundante=5, estado_aleatorio=5) # resumir el conjunto de datos imprimir(X.forma, y.forma) |
Ejecutando el ejemplo se crea el conjunto de datos y se resume la forma de los componentes de entrada y salida.
A continuación, podemos establecer una línea de base en el rendimiento. Desarrollaremos un árbol de decisiones para el conjunto de datos y lo evaluaremos usando la validación cruzada estratificada k-doble con tres repeticiones y 10 pliegues.
Los resultados se comunicarán como la media y la desviación estándar de la precisión de la clasificación en todas las repeticiones y pliegues.
El ejemplo completo figura a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# Evaluar un árbol de decisión sobre el conjunto de datos de clasificación de numpy importación significa de numpy importación std de sklearn.conjuntos de datos importación make_classification de sklearn.model_selection importación puntaje_valor_cruzado de sklearn.model_selection importación RepeatedStratifiedKFold de sklearn.árbol importación DecisionTreeClassifier # Definir el conjunto de datos X, y = make_classification(n_muestras=1000, n_funciones=20, n_informativo=15, n_redundante=5, estado_aleatorio=5) # Definir el modelo de conjunto subespacial aleatorio modelo = DecisionTreeClassifier() # Definir el método de evaluación cv = RepeatedStratifiedKFold(n_splits=10, n_repeticiones=3, estado_aleatorio=1) # Evaluar el modelo en el conjunto de datos n_puntuaciones = puntaje_valor_cruzado(modelo, X, y, puntuación=«exactitud, cv=cv, n_jobs=–1) # Informe de rendimiento imprimir(«Precisión media: %.3f (%.3f) % (significa(n_puntuaciones), std(n_puntuaciones))) |
La ejecución del ejemplo informa de la precisión de la clasificación de la media y la desviación estándar.
Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o el procedimiento de evaluación, o las diferencias en la precisión numérica. Considere ejecutar el ejemplo unas cuantas veces y compare el resultado promedio.
En este caso, podemos ver que un único modelo de árbol de decisión alcanza una precisión de clasificación de aproximadamente el 79,4 por ciento. Podemos utilizar esto como línea de base en el rendimiento para ver si nuestros conjuntos de selección de características son capaces de lograr un mejor rendimiento.
|
Precisión media: 0,794 (0,046) |
A continuación, exploremos usando diferentes métodos de selección de características como base para los conjuntos.
El método de selección de una sola característica se ensambla
En esta sección, exploraremos la creación de un conjunto a partir de los rasgos seleccionados por los métodos de selección de rasgos individuales.
Para un determinado método de selección de características, lo aplicaremos repetidamente con diferentes números de características seleccionadas para crear múltiples subespacios de características. Luego entrenaremos un modelo en cada uno, en este caso, un árbol de decisión, y combinaremos las predicciones.
Hay muchas maneras de combinar las predicciones, pero para mantener las cosas simples, usaremos un conjunto de votación que puede ser configurado para usar la votación dura o blanda para la clasificación, o el promedio para la regresión. Para mantener los ejemplos simples, nos centraremos en la clasificación y utilizaremos la votación dura, ya que los árboles de decisión no predicen las probabilidades calibradas, lo que hace que la votación blanda sea menos apropiada.
Para aprender más sobre los grupos de votación, vea el tutorial:
Cada modelo del conjunto de votación será un Pipeline en el que el primer paso es un método de selección de características, configurado para seleccionar un número específico de características, seguido de un modelo de clasificación de árbol de decisión.
Crearemos un subespacio de selección de características para cada número de columnas en el conjunto de datos de entrada de 1 al número de columnas. Esto se eligió arbitrariamente por simplicidad y puede que quieras experimentar con diferentes números de características en el conjunto, como números impares de características, o métodos más elaborados.
Como tal, podemos definir una función de ayuda llamada get_ensemble() que crea un conjunto de votación con miembros basados en la selección de características para un número determinado de características de entrada. Podemos entonces usar esta función como una plantilla para explorar usando diferentes métodos de selección de características.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# Obtener un conjunto de modelos votantes def get_ensemble(n_funciones): # Definir los modelos de base modelos = lista() # enumerar las características del conjunto de datos de entrenamiento para i en rango(1, n_funciones+1): # crear la selección de la característica transformar fs = ... # Crear el modelo modelo = DecisionTreeClassifier() # crear el oleoducto tubería = Oleoducto([[(«fs,fs), (‘m’, modelo)]) # Agregar como una tupla a la lista de modelos para votar modelos.anexar((str(i),tubería)) # Definir el conjunto de votos conjunto = VotingClassifier(estimadores=modelos, votación=«duro) volver conjunto |
Dado que estamos trabajando con un conjunto de datos de clasificación, exploraremos tres métodos diferentes de selección de características:
- ANOVA F-estadística.
- Información mutua.
- Selección de características recursivas.
Echemos un vistazo más de cerca a cada uno.
Conjunto F-estadístico ANOVA
ANOVA es un acrónimo de «análisis de la varianza» y es una prueba de hipótesis estadística paramétrica para determinar si las medias de dos o más muestras de datos (a menudo tres o más) proceden de la misma distribución o no.
Una estadística F, o prueba F, es una clase de pruebas estadísticas que calculan la relación entre los valores de las varianzas, como la varianza de dos muestras diferentes o la varianza explicada e inexplicada por una prueba estadística, como el ANOVA. El método ANOVA es un tipo de estadística F que aquí se denomina prueba F de ANOVA.
La biblioteca de la máquina de aprendizaje de ciencias proporciona una implementación del test ANOVA F en la función f_classif(). Esta función puede ser usada en una estrategia de selección de características, como la selección de la parte superior k las características más relevantes (valores más grandes) a través de la clase SelectKBest.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# Obtener un conjunto de modelos votantes def get_ensemble(n_funciones): # Definir los modelos de base modelos = lista() # enumerar las características del conjunto de datos de entrenamiento para i en rango(1, n_funciones+1): # crear la selección de la característica transformar fs = SelectKBest(score_func=f_classif, k=i) # Crear el modelo modelo = DecisionTreeClassifier() # crear el oleoducto tubería = Oleoducto([[(«fs,fs), (‘m’, modelo)]) # Agregar como una tupla a la lista de modelos para votar modelos.anexar((str(i),tubería)) # Definir el conjunto de votos conjunto = VotingClassifier(estimadores=modelos, votación=«duro) volver conjunto |
Enlazando todo esto, el ejemplo que se presenta a continuación evalúa un conjunto de votación compuesto por modelos que encajan en subespacios de características seleccionadas por la estadística F de ANOVA.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
# Ejemplo de un conjunto creado a partir de características seleccionadas con el anova f-estadístico de numpy importación significa de numpy importación std de sklearn.conjuntos de datos importación make_classification de sklearn.model_selection importación puntaje_valor_cruzado de sklearn.model_selection importación RepeatedStratifiedKFold de sklearn.selección_de_características importación SelectKBest de sklearn.selección_de_características importación f_classif de sklearn.árbol importación DecisionTreeClassifier de sklearn.conjunto importación VotingClassifier de sklearn.tubería importación Oleoducto de matplotlib importación pyplot # Obtener un conjunto de modelos votantes def get_ensemble(n_funciones): # Definir los modelos de base modelos = lista() # enumerar las características del conjunto de datos de entrenamiento para i en rango(1, n_funciones+1): # crear la selección de la característica transformar fs = SelectKBest(score_func=f_classif, k=i) # Crear el modelo modelo = DecisionTreeClassifier() # crear el oleoducto tubería = Oleoducto([[(«fs,fs), (‘m’, modelo)]) # Agregar como una tupla a la lista de modelos para votar modelos.anexar((str(i),tubería)) # Definir el conjunto de votos conjunto = VotingClassifier(estimadores=modelos, votación=«duro) volver conjunto # Definir el conjunto de datos X, y = make_classification(n_muestras=1000, n_funciones=20, n_informativo=15, n_redundante=5, estado_aleatorio=5) # Obtener el modelo de conjunto conjunto = get_ensemble(X.forma[[1]) # Definir el método de evaluación cv = RepeatedStratifiedKFold(n_splits=10, n_repeticiones=3, estado_aleatorio=1) # Evaluar el modelo en el conjunto de datos n_puntuaciones = puntaje_valor_cruzado(conjunto, X, y, puntuación=«exactitud, cv=cv, n_jobs=–1) # Informe de rendimiento imprimir(«Precisión media: %.3f (%.3f) % (significa(n_puntuaciones), std(n_puntuaciones))) |
La ejecución del ejemplo informa de la precisión de la clasificación de la media y la desviación estándar.
Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o el procedimiento de evaluación, o las diferencias en la precisión numérica. Considere ejecutar el ejemplo unas cuantas veces y compare el resultado promedio.
En este caso, podemos ver un aumento en el rendimiento sobre un solo modelo que alcanzó una precisión de alrededor del 79,4 por ciento a alrededor del 83,2 por ciento utilizando un conjunto de modelos en características seleccionadas por el ANOVA F-statistic.
|
Precisión media: 0,832 (0,043) |
A continuación, exploremos usando la información mutua.
Conjunto de información mutua
La información mutua del campo de la teoría de la información es la aplicación de la ganancia de información (típicamente utilizada en la construcción de árboles de decisión) para la selección de características.
La información mutua se calcula entre dos variables y mide la reducción de la incertidumbre para una variable dado un valor conocido de la otra variable. Es sencillo cuando se considera la distribución de dos variables discretas (categóricas u ordinales), como los datos de entrada categóricos y los datos de salida categóricos. No obstante, puede adaptarse para su uso con datos de entrada numéricos y de salida categóricos.
La biblioteca de aprendizaje de máquinas scikit-learn proporciona una implementación de información mutua para la selección de características con variables de entrada numérica y salida categórica a través de la función mutual_info_classif(). Como f_classif()puede ser usado en el SelectKBest estrategia de selección de características (y otras estrategias).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# Obtener un conjunto de modelos votantes def get_ensemble(n_funciones): # Definir los modelos de base modelos = lista() # enumerar las características del conjunto de datos de entrenamiento para i en rango(1, n_funciones+1): # crear la selección de la característica transformar fs = SelectKBest(score_func=mutual_info_classif, k=i) # Crear el modelo modelo = DecisionTreeClassifier() # crear el oleoducto tubería = Oleoducto([[(«fs,fs), (‘m’, modelo)]) # Agregar como una tupla a la lista de modelos para votar modelos.anexar((str(i),tubería)) # Definir el conjunto de votos conjunto = VotingClassifier(estimadores=modelos, votación=«duro) volver conjunto |
Enlazando todo esto, el ejemplo que se presenta a continuación evalúa un conjunto de votación compuesto por modelos que se ajustan a subespacios de características seleccionadas por información mutua.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
# ejemplo de un conjunto creado a partir de características seleccionadas con información mutua de numpy importación significa de numpy importación std de sklearn.conjuntos de datos importación make_classification de sklearn.model_selection importación puntaje_valor_cruzado de sklearn.model_selection importación RepeatedStratifiedKFold de sklearn.selección_de_funciones importación SelectKBest de sklearn.selección_de_características importación mutual_info_classif de sklearn.árbol importación DecisionTreeClassifier de sklearn.conjunto importación VotingClassifier de sklearn.tubería importación Oleoducto de matplotlib importación pyplot # Obtener un conjunto de modelos votantes def get_ensemble(n_funciones): # Definir los modelos de base modelos = lista() # enumerar las características del conjunto de datos de entrenamiento para i en rango(1, n_funciones+1): # crear la selección de la característica transformar fs = SelectKBest(score_func=mutual_info_classif, k=i) # Crear el modelo modelo = DecisionTreeClassifier() # crear el oleoducto tubería = Oleoducto([[(«fs,fs), (‘m’, modelo)]) # Agregar como una tupla a la lista de modelos para votar modelos.anexar((str(i),tubería)) # Definir el conjunto de votos conjunto = VotingClassifier(estimadores=modelos, votación=«duro) volver conjunto # Definir el conjunto de datos X, y = make_classification(n_muestras=1000, n_funciones=20, n_informativo=15, n_redundante=5, estado_aleatorio=5) # Obtener el modelo de conjunto conjunto = get_ensemble(X.forma[[1]) # Definir el método de evaluación cv = RepeatedStratifiedKFold(n_splits=10, n_repeticiones=3, estado_aleatorio=1) # Evaluar el modelo en el conjunto de datos n_puntuaciones = puntaje_valor_cruzado(conjunto, X, y, puntuación=«exactitud, cv=cv, n_jobs=–1) # Informe de rendimiento imprimir(«Precisión media: %.3f (%.3f) % (significa(n_puntuaciones), std(n_puntuaciones))) |
La ejecución del ejemplo informa de la precisión de la clasificación de la media y la desviación estándar.
Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o el procedimiento de evaluación, o las diferencias en la precisión numérica. Considere ejecutar el ejemplo unas cuantas veces y compare el resultado promedio.
En este caso, podemos ver un aumento en el rendimiento con respecto al uso de un solo modelo, aunque ligeramente inferior a la característica de subespacio seleccionada, con el ANOVA F-statistic alcanzando una precisión media de alrededor del 82,7 por ciento.
|
Precisión media: 0,827 (0,048) |
A continuación, exploremos los subespacios seleccionados mediante RFE.
Conjunto de selección de características recursivas
La eliminación de características recursivas, o RFE para abreviar, funciona mediante la búsqueda de un subconjunto de características comenzando con todas las características del conjunto de datos de entrenamiento y eliminando con éxito las características hasta que quede el número deseado.
Esto se logra ajustando el algoritmo de aprendizaje de máquina utilizado en el núcleo del modelo, clasificando las características por su importancia, descartando las características menos importantes y volviendo a ajustar el modelo. Este proceso se repite hasta que quede un número determinado de características.
Para más información sobre RFE, vea el tutorial:
El método RFE está disponible a través de la clase de RFE en scikit-learn y puede ser usado para la selección de características directamente. No es necesario combinarlo con el SelectKBest clase.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# Obtener un conjunto de modelos votantes def get_ensemble(n_funciones): # Definir los modelos de base modelos = lista() # enumerar las características del conjunto de datos de entrenamiento para i en rango(1, n_funciones+1): # crear la selección de la característica transformar fs = RFE(estimador=DecisionTreeClassifier(), n_funciones_para_seleccionar=i) # Crear el modelo modelo = DecisionTreeClassifier() # crear el oleoducto tubería = Oleoducto([[(«fs,fs), (‘m’, modelo)]) # Agregar como una tupla a la lista de modelos para votar modelos.anexar((str(i),tubería)) # Definir el conjunto de votos conjunto = VotingClassifier(estimadores=modelos, votación=«duro) volver conjunto |
Enlazando todo esto, el ejemplo que se presenta a continuación evalúa un conjunto de votación compuesto por modelos que encajan en subespacios de características seleccionadas por la RFE.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
# Ejemplo de un conjunto creado a partir de características seleccionadas con RFE de numpy importación significa de numpy importación std de sklearn.conjuntos de datos importación make_classification de sklearn.model_selection importación puntaje_valor_cruzado de sklearn.model_selection importación RepeatedStratifiedKFold de sklearn.selección_de_características importación RFE de sklearn.árbol importación DecisionTreeClassifier de sklearn.conjunto importación VotingClassifier de sklearn.tubería importación Oleoducto de matplotlib importación pyplot # Obtener un conjunto de modelos votantes def get_ensemble(n_funciones): # Definir los modelos de base modelos = lista() # enumerar las características del conjunto de datos de entrenamiento para i en rango(1, n_funciones+1): # crear la selección de la característica transformar fs = RFE(estimador=DecisionTreeClassifier(), n_funciones_para_seleccionar=i) # Crear el modelo modelo = DecisionTreeClassifier() # crear el oleoducto tubería = Oleoducto([[(«fs,fs), (‘m’, modelo)]) # Agregar como una tupla a la lista de modelos para votar modelos.anexar((str(i),tubería)) # Definir el conjunto de votos conjunto = VotingClassifier(estimadores=modelos, votación=«duro) volver conjunto # Definir el conjunto de datos X, y = make_classification(n_muestras=1000, n_funciones=20, n_informativo=15, n_redundante=5, estado_aleatorio=5) # Obtener el modelo de conjunto conjunto = get_ensemble(X.forma[[1]) # Definir el método de evaluación cv = RepeatedStratifiedKFold(n_splits=10, n_repeticiones=3, estado_aleatorio=1) # Evaluar el modelo en el conjunto de datos n_puntuaciones = puntaje_valor_cruzado(conjunto, X, y, puntuación=«exactitud, cv=cv, n_jobs=–1) # Informe de rendimiento imprimir(«Precisión media: %.3f (%.3f) % (significa(n_puntuaciones), std(n_puntuaciones))) |
La ejecución del ejemplo informa de la precisión de la clasificación de la media y la desviación estándar.
Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o el procedimiento de evaluación, o las diferencias en la precisión numérica. Considere ejecutar el ejemplo unas cuantas veces y compare el resultado promedio.
En este caso, podemos ver que la precisión media es similar a la observada con la selección de características de información mutua, con una puntuación de alrededor del 82,3 por ciento.
|
Precisión media: 0,823 (0,045) |
Este es un buen comienzo, y podría ser interesante ver si se pueden obtener mejores resultados utilizando conjuntos compuestos por menos miembros, por ejemplo, cada segundo, tercero o quinto número de características seleccionadas.
A continuación, veamos si podemos mejorar los resultados combinando modelos que encajen en subespacios de características seleccionadas por diferentes métodos de selección de características.
Conjuntos de selección de características combinadas
En la sección anterior, vimos que podemos obtener un aumento en el rendimiento sobre un modelo único utilizando un método de selección de características únicas como base de una predicción de conjunto para un conjunto de datos.
Esperábamos que las predicciones entre muchos de los miembros del conjunto estuvieran correlacionadas. Esto podría abordarse utilizando diferentes números de características de entrada seleccionadas como base del conjunto, en lugar de un número contiguo de características desde 1 hasta el número de columnas.
Un enfoque alternativo para introducir la diversidad consiste en seleccionar subespacios de características utilizando diferentes métodos de selección de características.
Exploraremos dos versiones de este enfoque. Con la primera, seleccionaremos el mismo número de características de cada método, y con la segunda, seleccionaremos un número contiguo de características desde 1 hasta el número de columnas para múltiples métodos.
Conjunto con un número fijo de características
En esta sección, haremos nuestro primer intento de diseñar un conjunto utilizando características seleccionadas por múltiples técnicas de selección de características.
Seleccionaremos un número arbitrario de características del conjunto de datos, luego usaremos cada uno de los tres métodos de selección de características para seleccionar un subespacio de características, ajustaremos un modelo de cada una y las usaremos como base para un conjunto de votación.
El get_ensemble() La función que se indica a continuación implementa esto, tomando como argumento el número especificado de características a seleccionar con cada método. Se espera que los rasgos seleccionados por cada método sean lo suficientemente diferentes y hábiles como para dar lugar a un conjunto efectivo.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# Obtener un conjunto de modelos votantes def get_ensemble(n_funciones): # Definir los modelos de base modelos = lista() # anova fs = SelectKBest(score_func=f_classif, k=n_funciones) anova = Oleoducto([[(«fs, fs), (‘m’, DecisionTreeClassifier())]) modelos.anexar((«anova, anova)) # Información mutua fs = SelectKBest(score_func=mutual_info_classif, k=n_funciones) mutinfo = Oleoducto([[(«fs, fs), (‘m’, DecisionTreeClassifier())]) modelos.anexar((«mutinfo, mutinfo)) # rfe fs = RFE(estimador=DecisionTreeClassifier(), n_funciones_para_seleccionar=n_funciones) rfe = Oleoducto([[(«fs, fs), (‘m’, DecisionTreeClassifier())]) modelos.anexar((«rfe, rfe)) # Definir el conjunto de votos conjunto = VotingClassifier(estimadores=modelos, votación=«duro) volver conjunto |
Enlazando todo esto, el ejemplo que se presenta a continuación evalúa un conjunto de un número fijo de características seleccionadas mediante diferentes métodos de selección de características.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 |
# Conjunto de un número fijo de características seleccionadas por diferentes métodos de selección de características de numpy importación significa de numpy importación std de sklearn.conjuntos de datos importación make_classification de sklearn.model_selection importación puntaje_valor_cruzado de sklearn.model_selection importación RepeatedStratifiedKFold de sklearn.selección_de_características importación RFE de sklearn.selección_de_características importación SelectKBest de sklearn.selección_de_características importación mutual_info_classif de sklearn.selección_de_características importación f_classif de sklearn.árbol importación DecisionTreeClassifier de sklearn.conjunto importación VotingClassifier de sklearn.tubería importación Oleoducto de matplotlib importación pyplot # Obtener un conjunto de modelos votantes def get_ensemble(n_funciones): # Definir los modelos de base modelos = lista() # anova fs = SelectKBest(score_func=f_classif, k=n_funciones) anova = Oleoducto([[(«fs, fs), (‘m’, DecisionTreeClassifier())]) modelos.anexar((«anova, anova)) # Información mutua fs = SelectKBest(score_func=mutual_info_classif, k=n_funciones) mutinfo = Oleoducto([[(«fs, fs), (‘m’, DecisionTreeClassifier())]) modelos.anexar((«mutinfo, mutinfo)) # rfe fs = RFE(estimador=DecisionTreeClassifier(), n_funciones_para_seleccionar=n_funciones) rfe = Oleoducto([[(«fs, fs), (‘m’, DecisionTreeClassifier())]) modelos.anexar((«rfe, rfe)) # Definir el conjunto de votos conjunto = VotingClassifier(estimadores=modelos, votación=«duro) volver conjunto # Definir el conjunto de datos X, y = make_classification(n_muestras=1000, n_funciones=20, n_informativo=15, n_redundante=5, estado_aleatorio=1) # Obtener el modelo de conjunto conjunto = get_ensemble(15) # Definir el método de evaluación cv = RepeatedStratifiedKFold(n_splits=10, n_repeticiones=3, estado_aleatorio=1) # Evaluar el modelo en el conjunto de datos n_puntuaciones = puntaje_valor_cruzado(conjunto, X, y, puntuación=«exactitud, cv=cv, n_jobs=–1) # Informe de rendimiento imprimir(«Precisión media: %.3f (%.3f) % (significa(n_puntuaciones), std(n_puntuaciones))) |
La ejecución del ejemplo informa de la precisión de la clasificación de la media y la desviación estándar.
Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o el procedimiento de evaluación, o las diferencias en la precisión numérica. Considere ejecutar el ejemplo unas cuantas veces y compare el resultado promedio.
En este caso, podemos ver un modesto aumento del rendimiento respecto a las técnicas consideradas en la sección anterior, lo que resulta en una precisión media de clasificación de alrededor del 83,9%.
|
Precisión media: 0,839 (0,044) |
Una comparación más justa podría ser comparar este resultado con cada modelo individual que compone el conjunto.
El ejemplo actualizado realiza exactamente esta comparación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 |
# Comparación del conjunto de un número fijo de características con modelos individuales que encajan en cada conjunto de características de numpy importación significa de numpy importación std de sklearn.conjuntos de datos importación make_classification de sklearn.model_selection importación puntaje_valor_cruzado de sklearn.model_selection importación RepeatedStratifiedKFold de sklearn.selección_de_características importación RFE de sklearn.selección_de_características importación SelectKBest de sklearn.selección_de_funciones importación mutual_info_classif de sklearn.selección_de_funciones importación f_classif de sklearn.árbol importación DecisionTreeClassifier de sklearn.conjunto importación VotingClassifier de sklearn.tubería importación Oleoducto de matplotlib importación pyplot # Obtener un conjunto de modelos votantes def get_ensemble(n_funciones): # Definir los modelos de base modelos, nombres = lista(), lista() # anova fs = SelectKBest(score_func=f_classif, k=n_funciones) anova = Oleoducto([[(«fs, fs), (‘m’, DecisionTreeClassifier())]) modelos.anexar((«anova, anova)) nombres.anexar(«anova) # Información mutua fs = SelectKBest(score_func=mutual_info_classif, k=n_funciones) mutinfo = Oleoducto([[(«fs, fs), (‘m’, DecisionTreeClassifier())]) modelos.anexar((«mutinfo, mutinfo)) nombres.anexar(«mutinfo) # rfe fs = RFE(estimador=DecisionTreeClassifier(), n_funciones_para_seleccionar=n_funciones) rfe = Oleoducto([[(«fs, fs), (‘m’, DecisionTreeClassifier())]) modelos.anexar((«rfe, rfe)) nombres.anexar(«rfe) # Definir el conjunto de votos conjunto = VotingClassifier(estimadores=modelos, votación=«duro) nombres.anexar(«conjunto) volver nombres, [[anova, mutinfo, rfe, conjunto] # Definir el conjunto de datos X, y = make_classification(n_muestras=1000, n_funciones=20, n_informativo=15, n_redundante=5, estado_aleatorio=1) # Obtener el modelo de conjunto nombres, modelos = get_ensemble(15) # Evaluar cada modelo resultados = lista() para modelo,nombre en zip(modelos,nombres): # Definir el método de evaluación cv = RepeatedStratifiedKFold(n_splits=10, n_repeticiones=3, estado_aleatorio=1) # Evaluar el modelo en el conjunto de datos n_puntuaciones = puntaje_valor_cruzado(modelo, X, y, puntuación=«exactitud, cv=cv, n_jobs=–1) # Informe de rendimiento imprimir(«>%s: %.3f (%.3f) % (nombre, significa(n_puntuaciones), std(n_puntuaciones))) resultados.anexar(n_puntuaciones) # Grafica los resultados para compararlos… pyplot.Boxplot(resultados, etiquetas=nombres) pyplot.mostrar() |
La ejecución del ejemplo informa del rendimiento medio de cada modelo individual ajustado a las características seleccionadas y termina con el rendimiento del conjunto que combina los tres modelos.
Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o el procedimiento de evaluación, o las diferencias en la precisión numérica. Considere ejecutar el ejemplo unas cuantas veces y compare el resultado promedio.
En este caso, los resultados sugieren que el conjunto de los modelos que encajan en las características seleccionadas funciona mejor que cualquier modelo individual del conjunto, como es de esperar.
|
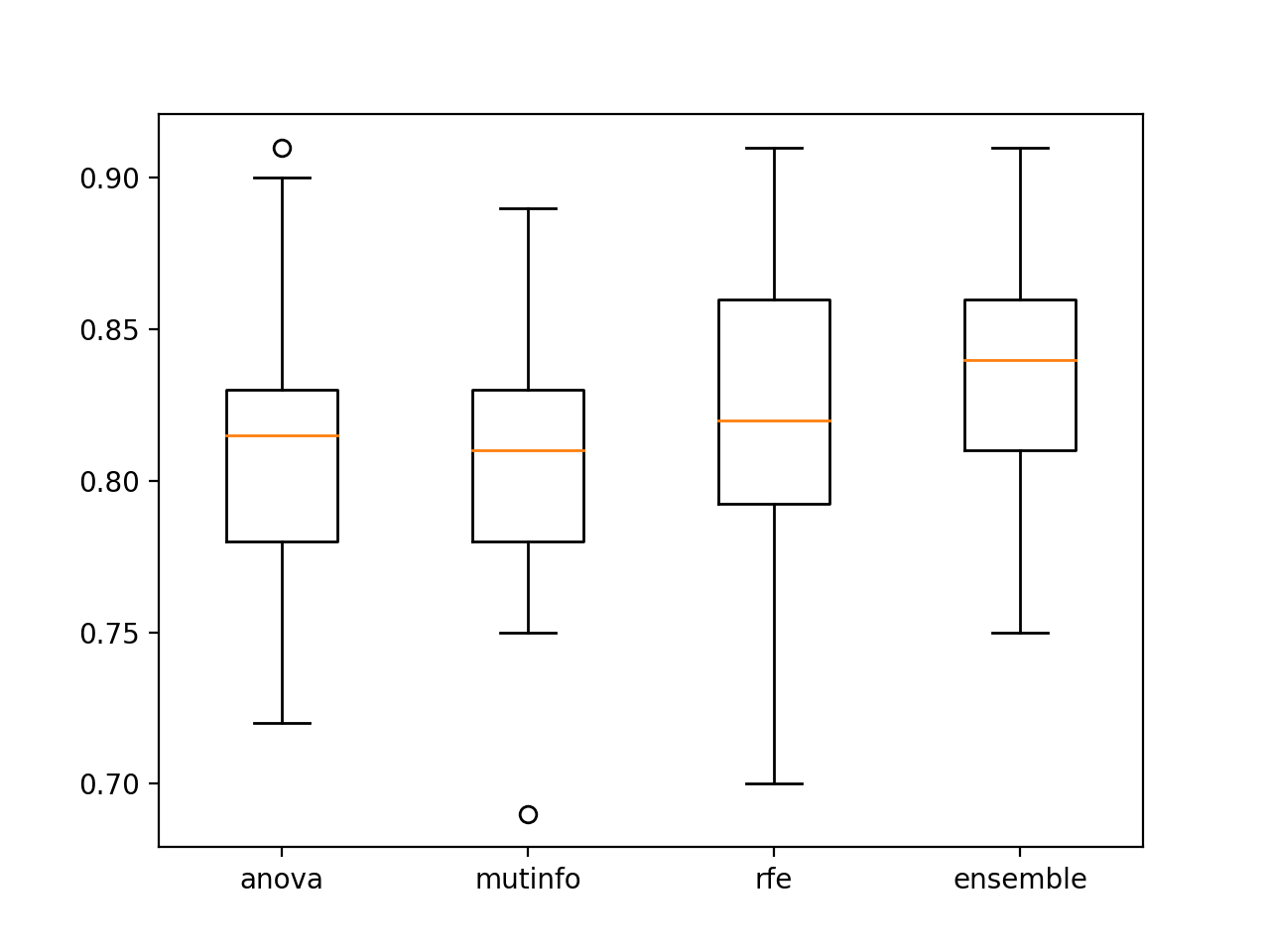
>anova: 0.811 (0.048) >mutinfo: 0.807 (0.041) >rfe: 0.825 (0.043) >ensamble: 0.837 (0.040) |
Se crea una figura para mostrar las gráficas de caja y bigote para cada conjunto de resultados, lo que permite comparar directamente las puntuaciones de la precisión de la distribución.
Podemos ver que la distribución del conjunto se inclina más y tiene una mayor precisión de clasificación media (línea naranja), confirmando visualmente el hallazgo.

Los diagramas de caja y bigote de la precisión del modelo de solteros encajan en las características seleccionadas vs. el conjunto
A continuación, exploremos la posibilidad de agregar varios miembros para cada método de selección de características.
Conjunto con un número contiguo de características
Podemos combinar los experimentos de la sección anterior con el experimento anterior.
Específicamente, podemos seleccionar múltiples subespacios de características usando cada método de selección de características, ajustar un modelo en cada uno y agregar todos los modelos a un solo conjunto.
En este caso, seleccionaremos el subespacio como hicimos en la sección anterior desde 1 hasta el número de columnas del conjunto de datos, aunque en este caso, repetiremos el proceso con cada método de selección de características.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
# Obtener un conjunto de modelos votantes def get_ensemble(n_features_start, n_features_end): # Definir los modelos de base modelos = lista() para i en rango(n_features_start, n_features_end+1): # anova fs = SelectKBest(score_func=f_classif, k=i) anova = Oleoducto([[(«fs, fs), (‘m’, DecisionTreeClassifier())]) modelos.anexar((«anova+str(i), anova)) # Información mutua fs = SelectKBest(score_func=mutual_info_classif, k=i) mutinfo = Oleoducto([[(«fs, fs), (‘m’, DecisionTreeClassifier())]) modelos.anexar((«mutinfo+str(i), mutinfo)) # rfe fs = RFE(estimador=DecisionTreeClassifier(), n_funciones_para_seleccionar=i) rfe = Oleoducto([[(«fs, fs), (‘m’, DecisionTreeClassifier())]) modelos.anexar((«rfe+str(i), rfe)) # Definir el conjunto de votos conjunto = VotingClassifier(estimadores=modelos, votación=«duro) volver conjunto |
Se espera que la diversidad de los rasgos seleccionados a través de los métodos de selección de rasgos dé lugar a un mayor aumento en el rendimiento del conjunto.
A continuación se muestra el ejemplo completo.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 |
# Conjunto de muchos subconjuntos de características seleccionadas por múltiples métodos de selección de características de numpy importación significa de numpy importación std de sklearn.conjuntos de datos importación make_classification de sklearn.model_selection importación puntaje_valor_cruzado de sklearn.model_selection importación RepeatedStratifiedKFold de sklearn.selección_de_características importación RFE de sklearn.selección_de_características importación SelectKBest de sklearn.selección_de_características importación mutual_info_classif de sklearn.selección_de_características importación f_classif de sklearn.árbol importación DecisionTreeClassifier de sklearn.conjunto importación VotingClassifier de sklearn.tubería importación Oleoducto de matplotlib importación pyplot # Obtener un conjunto de modelos votantes def get_ensemble(n_features_start, n_features_end): # Definir los modelos de base modelos = lista() para i en rango(n_features_start, n_features_end+1): # anova fs = SelectKBest(score_func=f_classif, k=i) anova = Oleoducto([[(«fs, fs), (‘m’, DecisionTreeClassifier())]) modelos.anexar((«anova+str(i), anova)) # Información mutua fs = SelectKBest(score_func=mutual_info_classif, k=i) mutinfo = Oleoducto([[(«fs, fs), (‘m’, DecisionTreeClassifier())]) modelos.anexar((«mutinfo+str(i), mutinfo)) # rfe fs = RFE(estimador=DecisionTreeClassifier(), n_funciones_para_seleccionar=i) rfe = Oleoducto([[(«fs, fs), (‘m’, DecisionTreeClassifier())]) modelos.anexar((«rfe+str(i), rfe)) # Definir el conjunto de votos conjunto = VotingClassifier(estimadores=modelos, votación=«duro) volver conjunto # Definir el conjunto de datos X, y = make_classification(n_muestras=1000, n_funciones=20, n_informativo=15, n_redundante=5, estado_aleatorio=1) # Obtener el modelo de conjunto conjunto = get_ensemble(1, 20) # Definir el método de evaluación cv = RepeatedStratifiedKFold(n_splits=10, n_repeticiones=3, estado_aleatorio=1) # Evaluar el modelo en el conjunto de datos n_puntuaciones = puntaje_valor_cruzado(conjunto, X, y, puntuación=«exactitud, cv=cv, n_jobs=–1) # Informe de rendimiento imprimir(«Precisión media: %.3f (%.3f) % (significa(n_puntuaciones), std(n_puntuaciones))) |
La ejecución del ejemplo informa de la precisión de la clasificación de la media y la desviación estándar del conjunto.
Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o el procedimiento de evaluación, o las diferencias en la precisión numérica. Considere ejecutar el ejemplo unas cuantas veces y compare el resultado promedio.
En este caso, podemos ver un nuevo aumento de la actuación como esperábamos, donde el conjunto combinado dio lugar a una precisión de clasificación media de alrededor del 86,0 por ciento.
|
Precisión media: 0,860 (0,036) |
El uso de la selección de características para seleccionar subespacios de características de entrada puede ser una alternativa interesante o tal vez un complemento de la selección de subespacios aleatorios.
Más lecturas
Esta sección proporciona más recursos sobre el tema si desea profundizar en él.
Tutoriales
Libros
APIs
Artículos
Resumen
En este tutorial, descubriste cómo desarrollar conjuntos subespaciales de selección de características con Python.
Específicamente, aprendiste:
- La selección de características proporciona una alternativa a los subespacios aleatorios para seleccionar grupos de características de entrada.
- Cómo desarrollar y evaluar conjuntos compuestos por características seleccionadas por técnicas de selección de características únicas.
- Cómo desarrollar y evaluar conjuntos compuestos por características seleccionadas por múltiples técnicas diferentes de selección de características.
¿Tiene alguna pregunta?
Haga sus preguntas en los comentarios de abajo y haré lo posible por responder.
