Recocido simulado es un algoritmo estocástico de optimización de búsqueda global.
Esto significa que utiliza la aleatoriedad como parte del proceso de búsqueda. Esto hace que el algoritmo sea apropiado para funciones objetivas no lineales donde otros algoritmos de búsqueda local no funcionan bien.
Como el algoritmo de búsqueda local estocástico de escalada de colinas, modifica una única solución y busca en el área relativamente local del espacio de búsqueda hasta que se localiza el óptimo local. A diferencia del algoritmo de escalada, puede aceptar peores soluciones como solución de trabajo actual.
La probabilidad de aceptar peores soluciones comienza alta al comienzo de la búsqueda y disminuye con el progreso de la búsqueda, lo que le da al algoritmo la oportunidad de ubicar primero la región para los óptimos globales, escapando de los óptimos locales y luego subir la colina hasta el mismo óptimo.
En este tutorial, descubrirá el algoritmo de optimización de recocido simulado para la optimización de funciones.
Después de completar este tutorial, sabrá:
- El recocido simulado es un algoritmo de búsqueda global estocástico para la optimización de funciones.
- Cómo implementar el algoritmo de recocido simulado desde cero en Python.
- Cómo utilizar el algoritmo de recocido simulado e inspeccionar los resultados del algoritmo.
Empecemos.

Recocido simulado desde cero en Python
Foto de Susanne Nilsson, algunos derechos reservados.
Descripción general del tutorial
Este tutorial se divide en tres partes; son:
- Recocido simulado
- Implementar recocido simulado
- Ejemplo resuelto de recocido simulado
Recocido simulado
El recocido simulado es un algoritmo estocástico de optimización de búsqueda global.
El algoritmo está inspirado en el recocido en metalurgia, donde el metal se calienta rápidamente a una temperatura alta y luego se enfría lentamente, lo que aumenta su resistencia y facilita el trabajo.
El proceso de recocido funciona primero excitando los átomos en el material a una temperatura alta, permitiendo que los átomos se muevan mucho, luego disminuyendo su excitación lentamente, permitiendo que los átomos caigan en una nueva configuración más estable.
Cuando están calientes, los átomos del material tienen más libertad para moverse y, mediante un movimiento aleatorio, tienden a asentarse en mejores posiciones. Un enfriamiento lento lleva el material a un estado cristalino ordenado.
– Página 128, Algoritmos de optimización, 2019.
El algoritmo de optimización de recocido simulado se puede considerar como una versión modificada de la escalada estocástica.
La escalada estocástica mantiene una única solución candidata y toma pasos de un tamaño aleatorio pero limitado del candidato en el espacio de búsqueda. Si el nuevo punto es mejor que el punto actual, entonces el punto actual se reemplaza por el nuevo punto. Este proceso continúa durante un número fijo de iteraciones.
El recocido simulado ejecuta la búsqueda de la misma manera. La principal diferencia es que a veces se aceptan puntos nuevos que no son tan buenos como el punto actual (puntos peores).
Un peor punto se acepta probabilísticamente donde la probabilidad de aceptar una solución peor que la solución actual es una función de la temperatura de la búsqueda y cuánto peor es la solución que la solución actual.
El algoritmo varía de Hill-Climbing en su decisión de cuándo reemplazar S, la solución candidata original, con R, su hijo recién modificado. Específicamente: si R es mejor que S, siempre reemplazaremos S con R como de costumbre. Pero si R es peor que S, aún podemos reemplazar S con R con cierta probabilidad
– Página 23, Fundamentos de metaheurística, 2011.
La temperatura inicial para la búsqueda se proporciona como un hiperparámetro y disminuye con el progreso de la búsqueda. Se pueden usar varios esquemas diferentes (programas de recocido) para disminuir la temperatura durante la búsqueda desde el valor inicial a un valor muy bajo, aunque es común calcular la temperatura en función del número de iteración.
Un ejemplo popular para calcular la temperatura es el llamado «recocido simulado rápido, ”Calculado de la siguiente manera
- temperatura = temperatura_inicial / (número_de_ iteración + 1)
Agregamos uno al número de iteración en el caso de que los números de iteración comiencen en cero, para evitar un error de división por cero.
La aceptación de las peores soluciones utiliza la temperatura, así como la diferencia entre la evaluación de la función objetivo de la peor solución y la solución actual. Se calcula un valor entre 0 y 1 utilizando esta información, lo que indica la probabilidad de aceptar la peor solución. Luego, esta distribución se muestrea utilizando un número aleatorio, que, si es menor que el valor, significa que se acepta la peor solución.
Es esta probabilidad de aceptación, conocida como criterio de Metropolis, la que permite que el algoritmo escape de los mínimos locales cuando la temperatura es alta.
– Página 128, Algoritmos de optimización, 2019.
Esto se denomina criterio de aceptación de metrópolis y para la minimización se calcula de la siguiente manera:
- criterio = exp (- (objetivo (nuevo) – objetivo (actual)) / temperatura)
Dónde Exp() es e (la constante matemática) elevado a una potencia del argumento proporcionado, y objetivo (nuevo), y objetivo (actual) son la evaluación de la función objetiva de las soluciones candidatas nuevas (peores) y actuales.
El efecto es que las soluciones deficientes tienen más posibilidades de ser aceptadas al principio de la búsqueda y menos probabilidades de ser aceptadas más adelante en la búsqueda. La intención es que la temperatura alta al comienzo de la búsqueda ayude a la búsqueda a ubicar la cuenca para el óptimo global y la temperatura baja más adelante en la búsqueda ayudará al algoritmo a enfocarse en el óptimo global.
La temperatura empieza alta, permitiendo que el proceso se mueva libremente por el espacio de búsqueda, con la esperanza de que en esta fase el proceso encuentre una buena región con el mejor mínimo local. Luego, la temperatura se baja lentamente, reduciendo la estocasticidad y obligando a la búsqueda a converger al mínimo.
– Página 128, Algoritmos de optimización, 2019.
Ahora que estamos familiarizados con el algoritmo de recocido simulado, veamos cómo implementarlo desde cero.
Implementar recocido simulado
En esta sección, exploraremos cómo podríamos implementar el algoritmo de optimización de recocido simulado desde cero.
Primero, debemos definir nuestra función objetivo y los límites de cada variable de entrada a la función objetivo. La función objetivo es solo una función de Python que nombraremos objetivo(). Los límites serán una matriz 2D con una dimensión para cada variable de entrada que define el mínimo y el máximo para la variable.
Por ejemplo, una función objetivo unidimensional y límites se definirían de la siguiente manera:
|
# función objetiva def objetivo(X): regreso 0 # definir rango para entrada límites = asarray([[[[–5,0, 5,0]]) |
Luego, podemos generar nuestro punto inicial como un punto aleatorio dentro de los límites del problema, luego evaluarlo usando la función objetivo.
|
... # generar un punto inicial mejor = límites[[:, 0] + rand(len(límites)) * (límites[[:, 1] – límites[[:, 0]) # evaluar el punto inicial best_eval = objetivo(mejor) |
Necesitamos mantener el «Actual”Solución que es el foco de la búsqueda y que puede ser reemplazada por mejores soluciones.
|
... # solución de trabajo actual curr, curr_eval = mejor, best_eval |
Ahora podemos recorrer un número predefinido de iteraciones del algoritmo definido como «n_iteraciones“, Como 100 o 1.000.
|
... # ejecutar el algoritmo por I en abarcar(n_iteraciones): ... |
El primer paso de la iteración del algoritmo es generar una nueva solución candidata a partir de la solución de trabajo actual, p. Ej. Da un paso.
Esto requiere un «Numero de pie”Parámetro, que es relativo a los límites del espacio de búsqueda. Daremos un paso aleatorio con una distribución gaussiana donde la media es nuestro punto actual y la desviación estándar está definida por «Numero de pie“. Eso significa que alrededor del 99 por ciento de los pasos que se tomen estarán dentro 3 * tamaño_paso del punto actual.
|
... # Da un paso candidato = solución + randn(len(límites)) * Numero de pie |
No tenemos que tomar medidas de esta manera. Es posible que desee utilizar una distribución uniforme entre 0 y el tamaño del paso. Por ejemplo:
|
... # Da un paso candidato = solución + rand(len(límites)) * Numero de pie |
A continuación, necesitamos evaluarlo.
|
... # evaluar el punto candidato candidte_eval = objetivo(candidato) |
Luego, debemos verificar si la evaluación de este nuevo punto es tan buena o mejor que el mejor punto actual, y si lo es, reemplazar nuestro mejor punto actual con este nuevo punto.
Esto es independiente de la solución de trabajo actual que es el foco de la búsqueda.
|
... # buscar nueva mejor solución si candidato_eval < best_eval: # almacenar nuevo mejor punto mejor, best_eval = candidato, candidato_eval # informe de progreso imprimir(‘>% d f (% s) =% .5f’ % (I, mejor, best_eval)) |
A continuación, debemos prepararnos para reemplazar la solución de trabajo actual.
El primer paso es calcular la diferencia entre la evaluación de la función objetivo de la solución actual y la solución de trabajo actual.
|
... # diferencia entre el candidato y la evaluación de puntos actual diff = candidato_eval – curr_eval |
A continuación, necesitamos calcular la temperatura actual, utilizando el programa de recocido rápido, donde «temperatura”Es la temperatura inicial proporcionada como argumento.
|
... # calcular la temperatura para la época actual t = temperatura / flotador(I + 1) |
Luego podemos calcular la probabilidad de aceptar una solución con peor desempeño que nuestra solución de trabajo actual.
|
... # calcular el criterio de aceptación de metrópolis metrópoli = Exp(–diff / t) |
Finalmente, podemos aceptar el nuevo punto como la solución de trabajo actual si tiene una mejor evaluación de la función objetivo (la diferencia es negativa) o si la función objetivo es peor, pero probabilísticamente decidimos aceptarlo.
|
... # comprobar si debemos mantener el nuevo punto si diff < 0 o rand() < metrópoli: # almacenar el nuevo punto actual curr, curr_eval = candidato, candidato_eval |
Y eso es.
Podemos implementar este algoritmo de recocido simulado como una función reutilizable que toma el nombre de la función objetivo, los límites de cada variable de entrada, las iteraciones totales, el tamaño del paso y la temperatura inicial como argumentos, y devuelve la mejor solución encontrada y su evaluación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
# algoritmo de recocido simulado def recocido_imulado(objetivo, límites, n_iteraciones, Numero de pie, temperatura): # generar un punto inicial mejor = límites[[:, 0] + rand(len(límites)) * (límites[[:, 1] – límites[[:, 0]) # evaluar el punto inicial best_eval = objetivo(mejor) # solución de trabajo actual curr, curr_eval = mejor, mejor_eval # ejecutar el algoritmo por I en abarcar(n_iteraciones): # Da un paso candidato = curr + randn(len(límites)) * paso_Talla # evaluar el punto candidato candidato_eval = objetivo(candidato) # buscar nueva mejor solución si candidato_eval < best_eval: # almacenar nuevo mejor punto mejor, best_eval = candidato, candidato_eval # informe de progreso imprimir(‘>% d f (% s) =% .5f’ % (I, mejor, best_eval)) # diferencia entre el candidato y la evaluación de puntos actual diff = candidato_eval – curr_eval # calcular la temperatura para la época actual t = temperatura / flotador(I + 1) # calcular el criterio de aceptación de metrópolis metrópoli = Exp(–diff / t) # comprobar si debemos mantener el nuevo punto si diff < 0 o rand() < metrópoli: # almacenar el nuevo punto actual curr, curr_eval = candidato, candidato_eval regreso [[mejor, best_eval] |
Ahora que sabemos cómo implementar el algoritmo de recocido simulado en Python, veamos cómo podríamos usarlo para optimizar una función objetivo.
Ejemplo resuelto de recocido simulado
En esta sección, aplicaremos el algoritmo de optimización de recocido simulado a una función objetivo.
Primero, definamos nuestra función objetivo.
Usaremos una función objetivo x ^ 2 unidimensional simple con los límites [-5, 5].
El siguiente ejemplo define la función, luego crea un gráfico de línea de la superficie de respuesta de la función para una cuadrícula de valores de entrada y marca el óptimo en f (0.0) = 0.0 con una línea roja
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 |
# función de optimización unimodal convexa desde numpy importar arange desde matplotlib importar pyplot # función objetiva def objetivo(X): regreso X[[0]**2.0 # definir rango para entrada r_min, r_max = –5,0, 5,0 # rango de entrada de muestra uniformemente en incrementos de 0.1 entradas = arange(r_min, r_max, 0,1) # calcular objetivos resultados = [[objetivo([[X]) por X en entradas] # crear una gráfica de línea de entrada vs resultado pyplot.trama(entradas, resultados) # definir el valor de entrada óptimo x_optima = 0.0 # dibuja una línea vertical en la entrada óptima pyplot.axvline(X=x_optima, ls=‘-‘, color=‘rojo’) # mostrar la trama pyplot.show() |
La ejecución del ejemplo crea un gráfico de líneas de la función objetivo y marca claramente la función óptima.
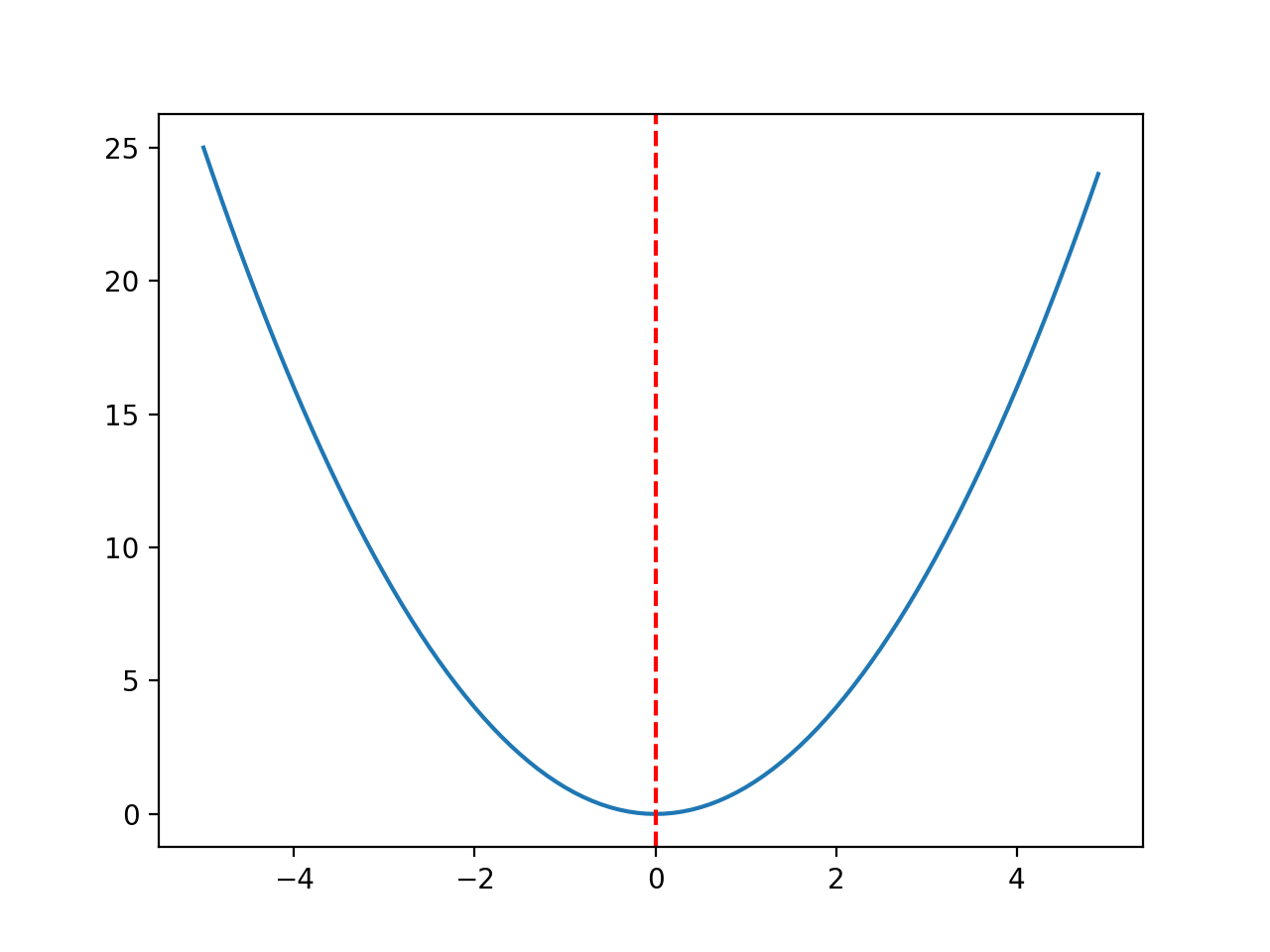
Gráfico de línea de la función objetivo con Optima marcado con una línea roja discontinua
Antes de aplicar el algoritmo de optimización al problema, tomemos un momento para comprender un poco mejor el criterio de aceptación.
Primero, el programa de recocido rápido es una función exponencial del número de iteraciones. Podemos aclarar esto creando un gráfico de la temperatura para cada iteración del algoritmo.
Usaremos una temperatura inicial de 10 y 100 iteraciones del algoritmo, ambas elegidas arbitrariamente.
El ejemplo completo se enumera a continuación.
|
# explorar la iteración de temperatura versus algoritmo para recocido simulado desde matplotlib importar pyplot # iteraciones totales del algoritmo iteraciones = 100 # temperatura inicial initial_temp = 10 # matriz de iteraciones de 0 a iteraciones – 1 iteraciones = [[I por I en abarcar(iteraciones)] # temperaturas para cada iteración temperaturas = [[initial_temp/flotador(I + 1) por I en iteraciones] # trazar iteraciones frente a temperaturas pyplot.trama(iteraciones, temperaturas) pyplot.xlabel(‘Iteración’) pyplot.etiquetarse(‘La temperatura’) pyplot.show() |
La ejecución del ejemplo calcula la temperatura para cada iteración del algoritmo y crea un gráfico de la iteración del algoritmo (eje x) frente a la temperatura (eje y).
Podemos ver que la temperatura cae rápidamente, exponencialmente, no linealmente, de modo que después de 20 iteraciones está por debajo de 1 y permanece baja durante el resto de la búsqueda.
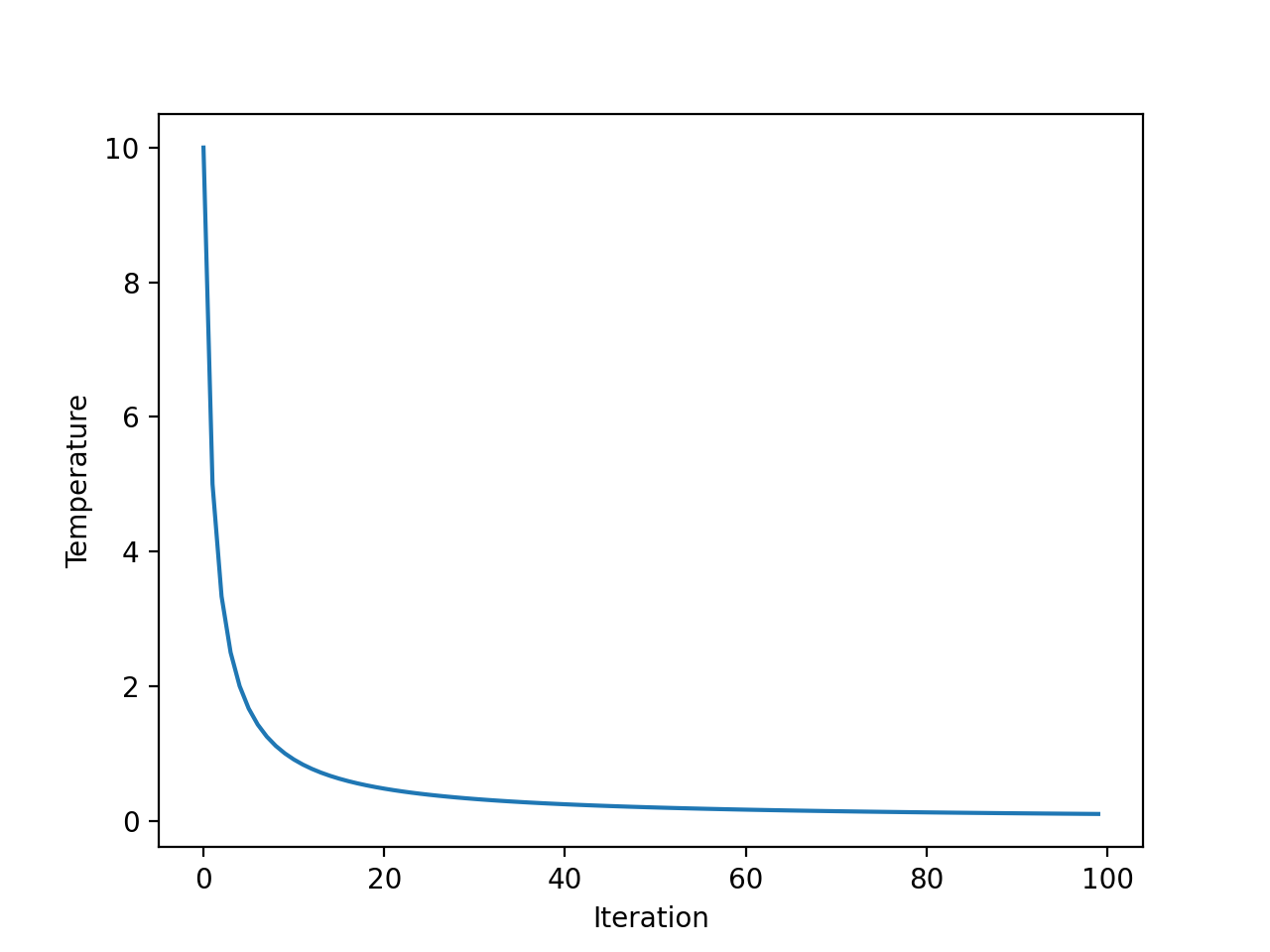
Gráfico de línea de temperatura frente a iteración del algoritmo para recocido rápido
A continuación, podemos tener una mejor idea de cómo cambia el criterio de aceptación de la metrópoli a lo largo del tiempo con la temperatura.
Recuerde que el criterio es una función de la temperatura, pero también es una función de cuán diferente es la evaluación objetiva del nuevo punto en comparación con la solución de trabajo actual. Como tal, trazaremos el criterio para algunos «diferencias en el valor de la función objetivo”Para ver el efecto que tiene sobre la probabilidad de aceptación.
El ejemplo completo se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 |
# explorar el criterio de aceptación de metrópolis para el recocido simulado desde Matemáticas importar Exp desde matplotlib importar pyplot # iteraciones totales del algoritmo iteraciones = 100 # temperatura inicial initial_temp = 10 # matriz de iteraciones de 0 a iteraciones – 1 iteraciones = [[I por I en abarcar(iteraciones)] # temperaturas para cada iteración temperaturas = [[initial_temp/flotador(I + 1) por I en iteraciones] # criterio de aceptación de metrópolis diferencias = [[0,01, 0,1, 1.0] por D en diferencias: metrópoli = [[Exp(–D/t) por t en temperaturas] # iteraciones de la trama vs metrópolis etiqueta = ‘diff =%. 2f’ % D pyplot.trama(iteraciones, metrópoli, etiqueta=etiqueta) # inalizar parcela pyplot.xlabel(‘Iteración’) pyplot.etiquetarse(‘Criterio de Metrópolis’) pyplot.leyenda() pyplot.show() |
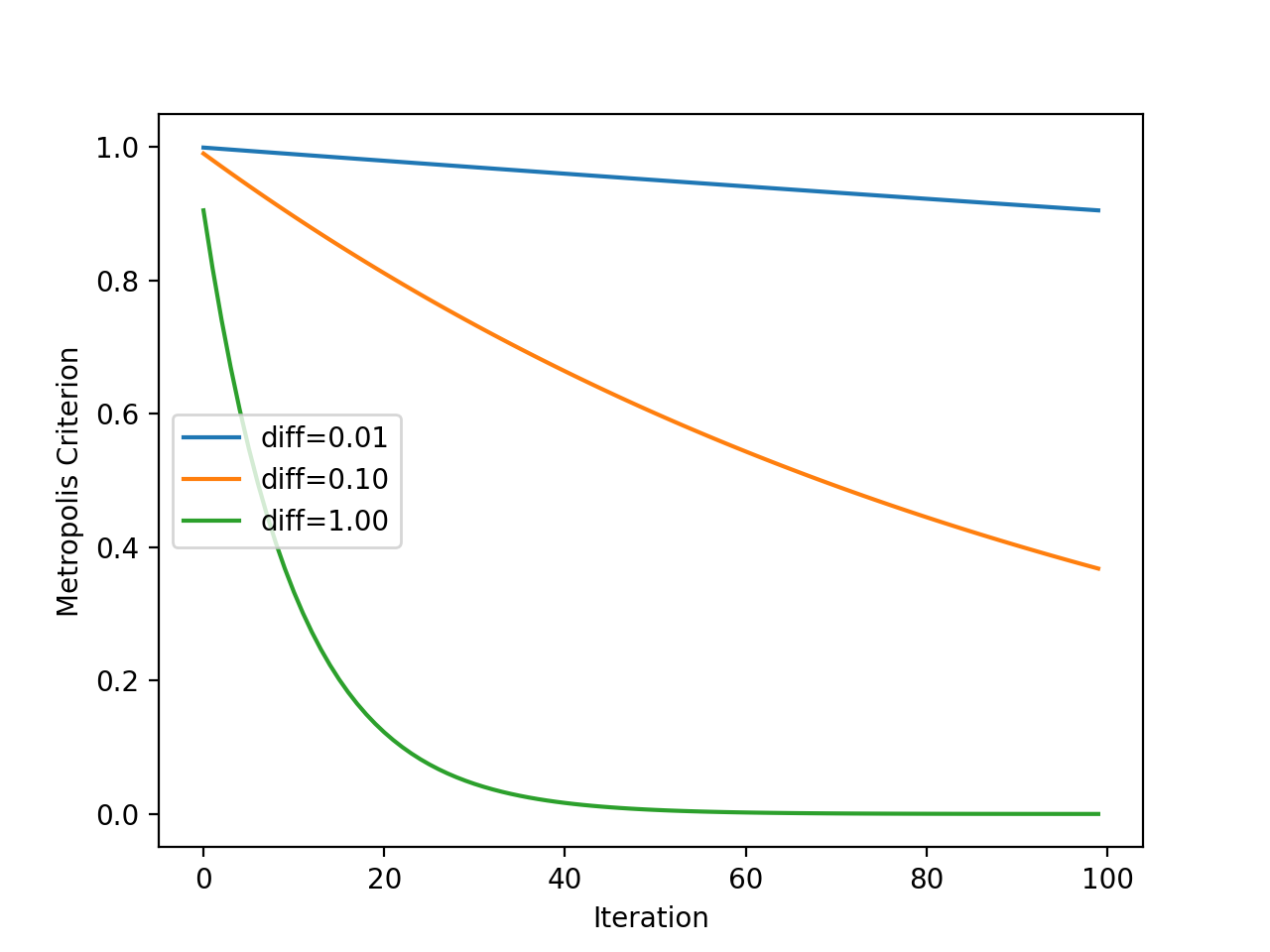
La ejecución del ejemplo calcula el criterio de aceptación de la metrópolis para cada iteración del algoritmo utilizando la temperatura que se muestra para cada iteración (que se muestra en la sección anterior).
La trama tiene tres líneas para tres diferencias entre la nueva solución peor y la solución de trabajo actual.
Podemos ver que cuanto peor es la solución (cuanto mayor es la diferencia), es menos probable que el modelo acepte la peor solución independientemente de la iteración del algoritmo, como podríamos esperar. También podemos ver que en todos los casos, la probabilidad de aceptar peores soluciones disminuye con la iteración del algoritmo.

Gráfico de línea del criterio de aceptación de Metropolis frente a la iteración del algoritmo para el recocido simulado
Ahora que estamos más familiarizados con el comportamiento de la temperatura y el criterio de aceptación de la metrópoli a lo largo del tiempo, apliquemos el recocido simulado a nuestro problema de prueba.
Primero, sembraremos el generador de números pseudoaleatorios.
Esto no es necesario en general, pero en este caso, quiero asegurarme de que obtengamos los mismos resultados (la misma secuencia de números aleatorios) cada vez que ejecutamos el algoritmo para que podamos trazar los resultados más tarde.
|
... # semilla del generador de números pseudoaleatorios semilla(1) |
A continuación, podemos definir la configuración de la búsqueda.
En este caso, buscaremos 1,000 iteraciones del algoritmo y usaremos un tamaño de paso de 0.1. Dado que estamos usando una función gaussiana para generar el paso, esto significa que aproximadamente el 99 por ciento de todos los pasos dados estarán a una distancia de (0.1 * 3) de un punto dado, p. tres desviaciones estándar.
También usaremos una temperatura inicial de 10.0. El procedimiento de búsqueda es más sensible al programa de recocido que a la temperatura inicial, por lo que los valores de temperatura inicial son casi arbitrarios.
|
... n_iteraciones = 1000 # definir el tamaño máximo de paso Numero de pie = 0,1 # temperatura inicial temperatura = 10 |
A continuación, podemos realizar la búsqueda y reportar los resultados.
|
... # realizar la búsqueda de recocido simulado mejor, puntaje = recocido_imulado(objetivo, límites, n_iteraciones, Numero de pie, temperatura) imprimir(‘¡Hecho!’) imprimir(‘f (% s) =% f’ % (mejor, puntaje)) |
Uniendo todo esto, el ejemplo completo se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 |
# búsqueda de recocido simulado de una función objetivo unidimensional desde numpy importar asarray desde numpy importar Exp desde numpy.aleatorio importar randn desde numpy.aleatorio importar rand desde numpy.aleatorio importar semilla # función objetiva def objetivo(X): regreso X[[0]**2.0 # simulated annealing algorithm def simulated_annealing(objective, bounds, n_iterations, step_size, temp): # generate an initial point best = bounds[[:, 0] + rand(len(bounds)) * (bounds[[:, 1] – bounds[[:, 0]) # evaluate the initial point best_eval = objective(best) # current working solution curr, curr_eval = best, best_eval # run the algorithm for i en range(n_iterations): # take a step candidate = curr + randn(len(bounds)) * step_size # evaluate candidate point candidate_eval = objective(candidate) # check for new best solution if candidate_eval < best_eval: # store new best point best, best_eval = candidate, candidate_eval # report progress print(‘>%d f(%s) = %.5f’ % (i, best, best_eval)) # difference between candidate and current point evaluation diff = candidate_eval – curr_eval # calculate temperature for current epoch t = temp / float(i + 1) # calculate metropolis acceptance criterion metropolis = exp(–diff / t) # check if we should keep the new point if diff < 0 o rand() < metropolis: # store the new current point curr, curr_eval = candidate, candidate_eval return [[best, best_eval] # seed the pseudorandom number generator seed(1) # define range for input bounds = asarray([[[[–5.0, 5.0]]) # define the total iterations n_iterations = 1000 # define the maximum step size step_size = 0,1 # initial temperature temp = 10 # perform the simulated annealing search best, score = simulated_annealing(objective, bounds, n_iterations, step_size, temp) print(‘Done!’) print(‘f(%s) = %f’ % (best, score)) |
Running the example reports the progress of the search including the iteration number, the input to the function, and the response from the objective function each time an improvement was detected.
At the end of the search, the best solution is found and its evaluation is reported.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, we can see about 20 improvements over the 1,000 iterations of the algorithm and a solution that is very close to the optimal input of 0.0 that evaluates to f(0.0) = 0.0.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 |
>34 f([-0.78753544]) = 0.62021 >35 f([-0.76914239]) = 0.59158 >37 f([-0.68574854]) = 0.47025 >39 f([-0.64797564]) = 0.41987 >40 f([-0.58914623]) = 0.34709 >41 f([-0.55446029]) = 0.30743 >42 f([-0.41775702]) = 0.17452 >43 f([-0.35038542]) = 0.12277 >50 f([-0.15799045]) = 0.02496 >66 f([-0.11089772]) = 0.01230 >67 f([-0.09238208]) = 0.00853 >72 f([-0.09145261]) = 0.00836 >75 f([-0.05129162]) = 0.00263 >93 f([-0.02854417]) = 0.00081 >144 f([0.00864136]) = 0.00007 >149 f([0.00753953]) = 0.00006 >167 f([-0.00640394]) = 0.00004 >225 f([-0.00044965]) = 0.00000 >503 f([-0.00036261]) = 0.00000 >512 f([0.00013605]) = 0.00000 Done! f([0.00013605]) = 0.000000 |
It can be interesting to review the progress of the search as a line plot that shows the change in the evaluation of the best solution each time there is an improvement.
We can update the simulated_annealing() to keep track of the objective function evaluations each time there is an improvement and return this list of scores.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
# simulated annealing algorithm def simulated_annealing(objective, bounds, n_iterations, step_size, temp): # generate an initial point best = bounds[[:, 0] + rand(len(bounds)) * (bounds[[:, 1] – bounds[[:, 0]) # evaluate the initial point best_eval = objective(best) # current working solution curr, curr_eval = best, best_eval # run the algorithm for i en range(n_iterations): # take a step candidate = curr + randn(len(bounds)) * step_size # evaluate candidate point candidate_eval = objective(candidate) # check for new best solution if candidate_eval < best_eval: # store new best point best, best_eval = candidate, candidate_eval # keep track of scores scores.append(best_eval) # report progress print(‘>%d f(%s) = %.5f’ % (i, best, best_eval)) # difference between candidate and current point evaluation diff = candidate_eval – curr_eval # calculate temperature for current epoch t = temp / float(i + 1) # calculate metropolis acceptance criterion metropolis = exp(–diff / t) # check if we should keep the new point if diff < 0 o rand() < metropolis: # store the new current point curr, curr_eval = candidate, candidate_eval return [[best, best_eval, scores] |
We can then create a line plot of these scores to see the relative change in objective function for each improvement found during the search.
|
... # line plot of best scores pyplot.plot(scores, ‘.-‘) pyplot.xlabel(‘Improvement Number’) pyplot.ylabel(‘Evaluation f(x)’) pyplot.show() |
Tying this together, the complete example of performing the search and plotting the objective function scores of the improved solutions during the search is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 sesenta y cinco 66 |
# simulated annealing search of a one-dimensional objective function desde numpy import asarray desde numpy import exp desde numpy.random import randn desde numpy.random import rand desde numpy.random import seed desde matplotlib import pyplot # objective function def objective(X): return X[[0]**2.0 # simulated annealing algorithm def simulated_annealing(objective, bounds, n_iterations, step_size, temp): # generate an initial point best = bounds[[:, 0] + rand(len(bounds)) * (bounds[[:, 1] – bounds[[:, 0]) # evaluate the initial point best_eval = objective(best) # current working solution curr, curr_eval = best, best_eval scores = list() # run the algorithm for i en range(n_iterations): # take a step candidate = curr + randn(len(bounds)) * step_size # evaluate candidate point candidate_eval = objective(candidate) # check for new best solution if candidate_eval < best_eval: # store new best point best, best_eval = candidate, candidate_eval # keep track of scores scores.append(best_eval) # report progress print(‘>%d f(%s) = %.5f’ % (i, best, best_eval)) # difference between candidate and current point evaluation diff = candidate_eval – curr_eval # calculate temperature for current epoch t = temp / float(i + 1) # calculate metropolis acceptance criterion metropolis = exp(–diff / t) # check if we should keep the new point if diff < 0 o rand() < metropolis: # store the new current point curr, curr_eval = candidate, candidate_eval return [[best, best_eval, scores] # seed the pseudorandom number generator seed(1) # define range for input bounds = asarray([[[[–5.0, 5.0]]) # define the total iterations n_iterations = 1000 # define the maximum step size step_size = 0,1 # initial temperature temp = 10 # perform the simulated annealing search best, score, scores = simulated_annealing(objective, bounds, n_iterations, step_size, temp) print(‘Done!’) print(‘f(%s) = %f’ % (best, score)) # line plot of best scores pyplot.plot(scores, ‘.-‘) pyplot.xlabel(‘Improvement Number’) pyplot.ylabel(‘Evaluation f(x)’) pyplot.show() |
Running the example performs the search and reports the results as before.
A line plot is created showing the objective function evaluation for each improvement during the hill climbing search. We can see about 20 changes to the objective function evaluation during the search with large changes initially and very small to imperceptible changes towards the end of the search as the algorithm converged on the optima.
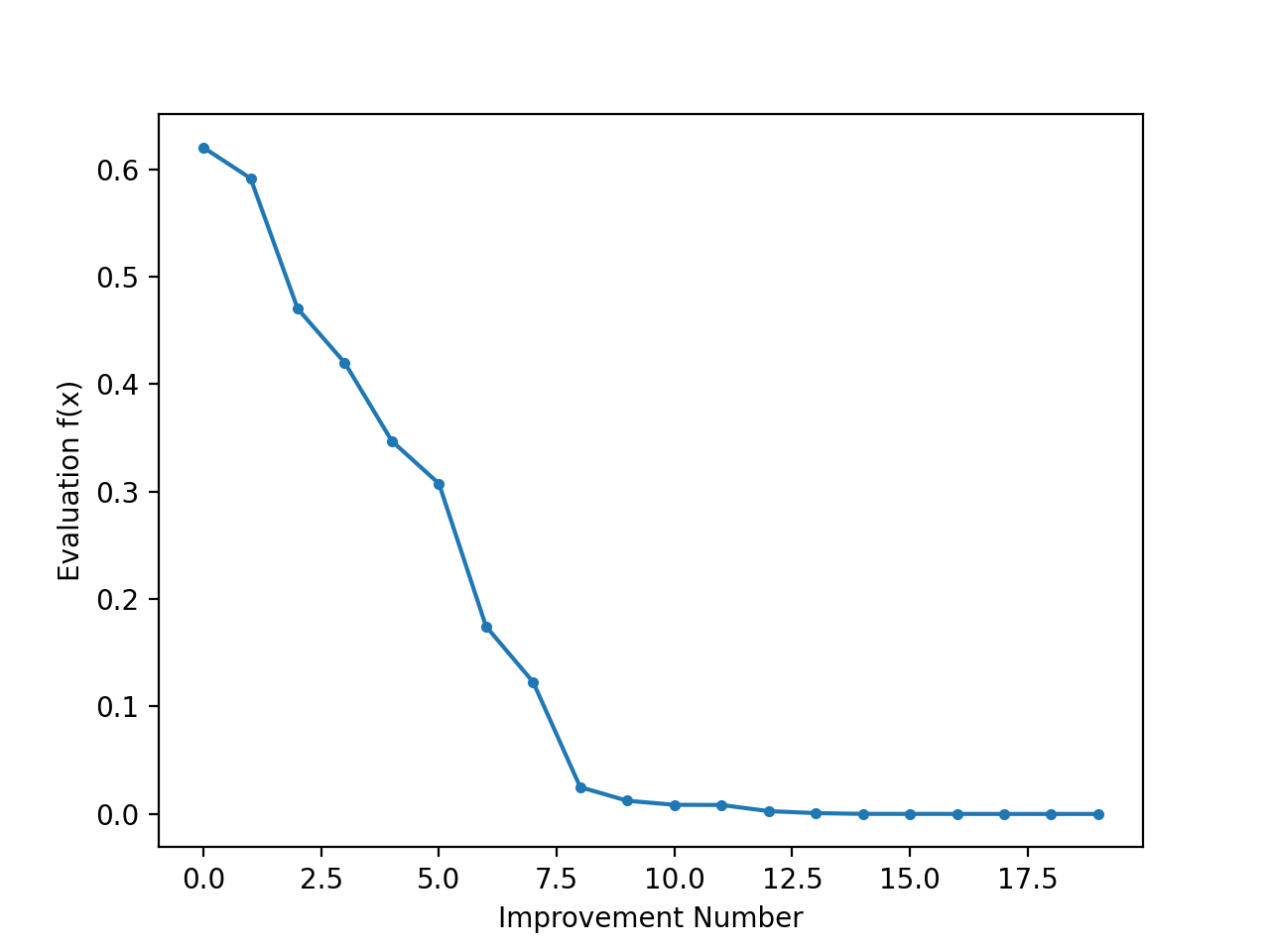
Line Plot of Objective Function Evaluation for Each Improvement During the Simulated Annealing Search
Further Reading
This section provides more resources on the topic if you are looking to go deeper.
Papers
Books
Articles
Resumen
In this tutorial, you discovered the simulated annealing optimization algorithm for function optimization.
Specifically, you learned:
- Simulated annealing is a stochastic global search algorithm for function optimization.
- How to implement the simulated annealing algorithm from scratch in Python.
- How to use the simulated annealing algorithm and inspect the results of the algorithm.
Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.
