El laboratorio de ciencia de datos
Generación de datos sintéticos utilizando una red de adversarios generativos (GAN) con PyTorch
El Dr. James McCaffrey de Microsoft Research explica una red de confrontación generativa, un sistema neuronal profundo que se puede usar para generar datos sintéticos para escenarios de aprendizaje automático, como generar machos sintéticos para un conjunto de datos que tiene muchas mujeres pero pocos hombres.
Una red generativa adversarial (GAN) es un sistema neuronal profundo que se puede utilizar para generar datos sintéticos. Las GAN se utilizan con mayor frecuencia con datos de imágenes, pero las GAN pueden crear cualquier tipo de datos. Los GAN son algo similares a los autocodificadores variacionales (VAE) en el sentido de que ambos sistemas generan datos sintéticos; sin embargo, los GAN son significativamente más complejos que los VAE.
La generación de datos sintéticos es útil en varios escenarios de aprendizaje automático. Un caso de uso es cuando tiene datos de entrenamiento desequilibrados para una clase en particular. Por ejemplo, en un conjunto de datos de información de maestros de escuela primaria, es posible que tenga muchas mujeres pero muy pocos hombres. Puede entrenar un GAN en los empleados masculinos y luego usar el GAN para generar elementos de datos masculinos sintéticos.
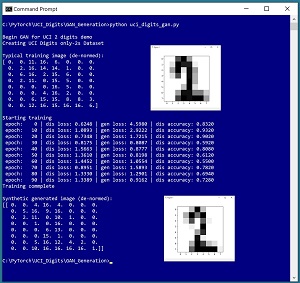
Una buena forma de ver hacia dónde se dirige este artículo es echar un vistazo a la captura de pantalla de un programa de demostración en Figura 1. La demostración genera imágenes sintéticas de «2» dígitos escritos a mano basándose en el conjunto de datos UCI Digits. Cada imagen es de 8 por 8 píxeles con valores entre 0 y 16. La demostración comienza cargando 380 imágenes reales de «2» dígitos en la memoria. Se muestra un dígito «2» típico de los datos de entrenamiento. A continuación, la demostración entrena un modelo GAN utilizando las 380 imágenes. La demostración finaliza utilizando el GAN entrenado para generar una imagen «2» sintética.
Este artículo asume que tiene una familiaridad intermedia o superior con un lenguaje de programación de la familia C, preferiblemente Python, y una familiaridad básica con la biblioteca de código PyTorch. El código fuente del programa de demostración es demasiado largo para presentarlo en su totalidad en este artículo, pero el código completo y los datos de entrenamiento están disponibles en la descarga del archivo adjunto. Los datos de entrenamiento están incrustados como comentarios en el código fuente.
Las GAN son complejas, tanto conceptual como técnicamente, por lo que este artículo se centra en explicar las ideas clave que necesita comprender para poder crear GAN que se adapten a sus escenarios de problemas. Se ha omitido todo el código de verificación de errores normal para mantener las ideas principales lo más claras posible.
Para ejecutar el programa de demostración, debe tener Python y PyTorch instalados en su máquina. Los programas de demostración se desarrollaron en Windows 10 utilizando la distribución Anaconda 2020.02 de 64 bits (que contiene Python 3.7.6) y la versión 1.8.0 de PyTorch para la CPU instalada a través de pip. La instalación no es trivial. Puede encontrar instrucciones detalladas de instalación paso a paso en la publicación de mi blog.
El conjunto de datos de dígitos de la UCI
El conjunto de datos UCI Digits se puede encontrar en línea. Hay un archivo de 3823 elementos llamado optdigits.tra (destinado a la capacitación) y un archivo de 1,797 elementos llamado optdigits.tes (para pruebas). Descargué los archivos y los renombré a optdigits_train_3823.txt y optdigits_test_1797.txt. Cada archivo es un archivo de texto simple delimitado por comas. Cada línea representa un dígito escrito a mano de 8 por 8 del «0» al «9».
Los datos de dígitos UCI se ven así:
0,1,6,16,12, . . . 1,0,0,13,0 2,7,8,11,15, . . . 16,0,7,4,1 . . .
Los primeros 64 valores de cada línea son los valores de píxeles de la imagen. Cada píxel es un valor de escala de grises entre 0 y 16. El último valor en cada línea es el dígito / etiqueta. Hay aproximadamente 380 de cada dígito en el archivo de entrenamiento y aproximadamente 180 de cada dígito en el archivo de prueba, pero los dígitos no están distribuidos uniformemente. Los recuentos de cada dígito «0» a «9» en los datos de entrenamiento son: 376, 389, 380, 389, 387, 376, 377, 387, 380 y 382.
Escribí un pequeño programa de utilidad para escanear el archivo de datos de entrenamiento y seleccionar los 380 «2» dígitos y guardarlos como archivo uci_digits_2_only.txt usando el mismo formato delimitado por comas.
El programa de demostración define una clase PyTorch Dataset para cargar los datos en la memoria. Ver Listado 1.
Listado 1: una clase de conjunto de datos para los datos de dígitos UCI
import torch as T
import numpy as np
class UCI_Digits_Dataset(T.utils.data.Dataset):
# like: 8,12,0,16, . . 15,7
# 64 pixel values [0-16], digit [0-9]
def __init__(self, src_file, n_rows=None):
tmp_x = np.loadtxt(src_file, max_rows=n_rows,
usecols=range(0,64), delimiter=",", comments="https://visualstudiomagazine.com/articles/2021/06/02/#",
dtype=np.float32) # just pixels, no labels
tmp_x /= 16.0 # normalize
self.x_data = T.tensor(tmp_x,
dtype=T.float32).to(device)
def __len__(self):
return len(self.x_data)
def __getitem__(self, idx):
return self.x_data[idx]
La clase carga un archivo de datos de dígitos UCI en la memoria como una matriz bidimensional usando la función NumPy loadtxt (). Los valores de los píxeles se normalizan en un rango de 0.0 a 1.0 dividiendo por 16, lo cual es importante para la arquitectura GAN. La matriz NumPy se convierte en un tensor de PyTorch y la función __getitem __ () entrega los elementos uno por uno.
El conjunto de datos se puede llamar así:
fn = ".\Data\ uci_digits_2_only.txt " my_ds = UCI_Digits_Dataset(fn) my_ldr = T.utils.data.DataLoader(my_ds, batch_size=10, shuffle=True) for (b_ix, batch) in enumerate(my_ldr): # b_ix is the batch index # batch has 10 items with 64 values between 0 and 1 . . .
El objeto Dataset se pasa a un objeto PyTorch DataLoader integrado. El objeto DataLoader sirve los datos en lotes de un tamaño específico, en un orden aleatorio en cada paso a través del conjunto de datos.
El patrón de diseño que se presenta aquí funcionará para la mayoría de los escenarios generativos de redes adversas. Si sus datos sin procesar contienen una variable categórica, como «color» con posibles valores «rojo», «azul» o «verde», puede codificar los datos de forma instantánea: «rojo» = (1, 0, 0), «azul» = (0, 1, 0), «verde» = (0, 0, 1).
Comprensión de las redes generativas de confrontación
Mi explicación de las redes generativas de confrontación tomará algunas libertades con la terminología y los detalles para ayudar a que la explicación sea más fácil de entender. En resumen, un GAN es un sistema que tiene dos redes neuronales profundas interconectadas. Una red se llama Generador; la otra red se llama Discriminador.
El generador acepta valores aleatorios y emite un elemento de datos sintéticos. El objetivo final de una GAN es generar buenos elementos de datos sintéticos.
El Discriminador es una red auxiliar que es un clasificador binario. El Discriminador acepta un elemento de datos, que puede ser real (de los datos de entrenamiento) o falso (del Generador), y luego emite un valor de pseudoprobabilidad entre 0 y 1, donde un valor menor a 0.5 indica un elemento falso y un un valor superior a 0,5 indica un artículo real.
Expresado en pseudocódigo de alto nivel, una iteración del entrenamiento de un GAN (para datos de imagen) es:
fetch a batch of real images from training data feed real images to Discriminator, compute loss make a batch of fake images using Generator feed fake images to Discriminator, compute loss combine the two loss values use combined loss to update Discriminator make a batch of fake images using Generator feed fake images to Discriminator, compute reverse loss use reverse loss to update Generator
El proceso de entrenamiento alterna entre actualizar el Discriminador, para que pueda detectar mejor las imágenes falsas producidas por el Generador, y actualizar el Generador para que produzca imágenes falsas que tienen más probabilidades de engañar al Discriminador. Cuando finaliza el entrenamiento, un buen Generador engañará al Discriminador aproximadamente la mitad de las veces, lo que significa que el Discriminador no puede distinguir fácilmente una imagen falsa de una imagen real.
Hay muchas alternativas de arquitectura y diseño posibles para una GAN. El diseño presentado en este artículo es relativamente simple y se basa principalmente en el artículo de investigación original de GAN de 2014 «Generative Adversarial Networks» de I. Goodfellow et al.
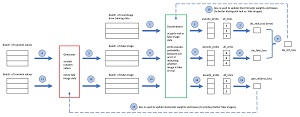
El diagrama en Figura 2 muestra la relación entre el generador y el discriminador, y una iteración de entrenamiento para la demostración GAN. Su reacción inmediata probablemente sea algo como «Eso parece bastante complicado». Estarías en lo correcto.
Los pasos 1 a 10 entrenan al clasificador binario Discriminador. Un clasificador binario regular no GAN se entrena utilizando datos que contienen elementos de datos de clase 0 y clase 1. En un GAN, los elementos de la clase 1 son las imágenes reales de los datos de entrenamiento y los elementos de la clase 0 son imágenes falsas del Generador. Los dos valores de pérdida se calculan por separado y luego se combinan sumando. Un diseño alternativo es construir un lote de datos reales y falsos combinados, enviar los datos combinados al Discriminador y calcular un valor de pérdida único.
Los pasos 11 al 16 entrenan al generador. Suponga que el generador crea un lote de imágenes falsas deficientes (12). El Discriminador identificará fácilmente las imágenes como falsas y la salida (14) será pseudoprobabilidades cercanas a 0. Cuando se compara con un tensor all_ones (15), el valor de pérdida será grande y los pesos de la red neuronal del Generador se actualizarán significativamente, mejorando el generador.
Pero supongamos que el generador crea un lote de imágenes falsas muy buenas. El Discriminador pensará que las imágenes son reales y, por lo tanto, las pseudoprobabilidades en (14) serán cercanas a 1. Cuando se compara con un tensor all_ones, la pérdida será muy pequeña y los pesos de la red neuronal del Generador no cambiarán mucho. ¡Inteligente!
Definición del generador GAN
El código que define la demostración GAN Generator se presenta en Listado 2. La arquitectura es 20-40-64, lo que significa que la red acepta 20 valores aleatorios, los expande a 40 valores intermedios. Luego, los 40 valores se expanden a 64 valores entre 0 y 1, donde cada uno es un píxel normalizado.
Listado 2: Definición de generador GAN
class Generator(T.nn.Module): # 20-40-64
def __init__(self):
super(Generator, self).__init__()
self.fc1 = T.nn.Linear(20, 40)
self.fc2 = T.nn.Linear(40, 64)
self.inpt_dim = 20
T.nn.init.xavier_uniform_(self.fc1.weight)
T.nn.init.zeros_(self.fc1.bias)
T.nn.init.xavier_uniform_(self.fc2.weight)
T.nn.init.zeros_(self.fc2.bias)
def forward(self, x): # 20
z = T.tanh(self.fc1(x)) # 40
oupt = T.sigmoid(self.fc2(z)) # 64
return oupt
La función de activación de salida es sigmoidea () de modo que una imagen falsa generada tendrá valores de píxeles normalizados entre 0 y 1. La activación de la capa oculta es tanh (). Una de las razones por las que las GAN son tan complicadas es que tanto el generador como el discriminador tienen muchos hiperparámetros, como el número de capas ocultas, la función de activación en los nodos ocultos, el algoritmo de inicialización de peso y sesgo y el tamaño de la entrada del generador.
Definición del discriminador de GAN
El código que define el clasificador binario GAN Discriminator demo se presenta en Listado 3. La arquitectura es 64-32-16-1, lo que significa que la red acepta 64 valores entre 0 y 1 que representan una imagen real o una imagen falsa. La red tiene un solo nodo de salida que, cuando se usa con pérdida de entropía cruzada binaria, es el diseño habitual de un clasificador binario.
Listado 3: Definición de discriminador de GAN
class Discriminator(T.nn.Module): # 64-32-16-1
def __init__(self):
super(Discriminator, self).__init__()
self.fc1 = T.nn.Linear(64, 32)
self.fc2 = T.nn.Linear(32, 16)
self.fc3 = T.nn.Linear(16, 1)
T.nn.init.xavier_uniform_(self.fc1.weight)
T.nn.init.zeros_(self.fc1.bias)
T.nn.init.xavier_uniform_(self.fc2.weight)
T.nn.init.zeros_(self.fc2.bias)
T.nn.init.xavier_uniform_(self.fc3.weight)
T.nn.init.zeros_(self.fc3.bias)
def forward(self, x): # 64
z = T.tanh(self.fc1(x)) # 32
z = T.tanh(self.fc2(z)) # 16
oupt = T.sigmoid(self.fc3(z)) # 1
return oupt
En resumen, al diseñar un GAN, el generador tendrá una arquitectura x- (yy) -z donde el número de nodos de salida, z, es igual al número de valores en un elemento de datos. La función de activación de salida suele ser sigmoidea (). El número de nodos de entrada, x, es un hiperparámetro. Una regla general que utilizo es comenzar probando sqrt (z) oz / 2 oz / 4 para el número de nodos de entrada. El número de capas ocultas y el número de nodos ocultos en cada capa, y, y la función de activación oculta son hiperparámetros. Una regla general para el número de nodos ocultos es probar un valor a la mitad entre el número de nodos de entrada y el número de nodos de salida. Por lo general, primero intento tanh () o relu () para la activación del nodo oculto.
El discriminador tendrá una arquitectura z- (ww) -1. El número de nodos de entrada, z, es igual al número de valores en un elemento de datos. El número de capas ocultas, el número de nodos en cada capa oculta y la función de activación en los nodos ocultos son hiperparámetros. A menudo, primero pruebo dos capas ocultas con nodos z / 2 yz / 4. Por lo general, intento la activación de nodo oculto tanh () o relu (). La activación del nodo de salida del Discriminador suele ser sigmoidea ().
Estructura general del programa
La estructura general del programa de demostración, con algunas ediciones menores para ahorrar espacio, se presenta en Listado 4. La demostración comienza con la importación de las bibliotecas centrales necesarias de NumPy y Torch. La biblioteca matplotlib se usa para mostrar imágenes, por lo que no la necesitará si sus elementos de datos no son imágenes.
Listado 4: Estructura general del programa GAN
# uci_digits_gan.py
# GAN to generate synthetic '2' digits
# PyTorch 1.8.0-CPU Anaconda3-2020.02 (Python 3.7.6)
# Windows 10
import numpy as np
import torch as T
import matplotlib as mpl
import matplotlib.pyplot as plt
device = T.device("cpu")
# -----------------------------------------------------------
class UCI_Digits_Dataset(T.utils.data.Dataset):
# see Listing 1
class Generator(T.nn.Module): # 20-40-64
# see Listing 2
class Discriminator(T.nn.Module): # 64-32-16-1
# see Listing 3
# -----------------------------------------------------------
def accuracy(gen, dis, n, verbose=False): . .
def display_digit(x, save=False): . .
def main():
# 0. get started
print("Begin GAN for UCI 2 digits demo ")
np.random.seed(0)
T.manual_seed(0)
np.set_printoptions(linewidth=36)
mpl.rcParams['toolbar'] = 'None'
# 1. create data objects
print("Creating UCI Digits only-2s Dataset ")
train_file = ".\Data\uci_digits_2_only.txt"
train_ds = UCI_Digits_Dataset(train_file)
bat_size = 10
train_ldr = T.utils.data.DataLoader(train_ds,
batch_size=bat_size, shuffle=True, drop_last=True)
# 1b. show typical training item (item [5])
print("Typical training image (de-normed): ")
digit = np.rint(train_ds[5].numpy() * 16)
print(digit)
display_digit(train_ds[5], save=False)
# 2. create networks
dis = Discriminator().to(device) # 64-32-16-1
gen = Generator().to(device) # 20-40-64
# 3. train GAN model
max_epochs = 100
ep_log_interval = 10
lrn_rate = 0.005
dis.train() # set mode
gen.train()
dis_optimizer = T.optim.Adam(dis.parameters(), lrn_rate)
gen_optimizer = T.optim.Adam(gen.parameters(), lrn_rate)
loss_func = T.nn.BCELoss()
all_ones = T.ones(bat_size, dtype=T.float32).to(device)
all_zeros = T.zeros(bat_size, dtype=T.float32).to(device)
print("Starting training ")
for epoch in range(0, max_epochs):
for (batch_idx, real_images) in enumerate(train_ldr):
dis_accum_loss = 0.0 # to display progress
gen_accum_loss = 0.0
# 3a. train discriminator using real images
dis_optimizer.zero_grad()
dis_real_oupt = dis(real_images).reshape(-1) # [0, 1]
dis_real_loss = loss_func(dis_real_oupt,
all_ones) # or use squeeze()
# 3b. train discriminator using fake images
zz = T.normal(0.0, 1.0,
size=(bat_size, gen.inpt_dim)).to(device) # 10 x 20
fake_images = gen(zz)
dis_fake_oupt = dis(fake_images).reshape(-1)
dis_fake_loss = loss_func(dis_fake_oupt, all_zeros)
dis_loss_tot = dis_real_loss + dis_fake_loss
dis_accum_loss += dis_loss_tot
dis_loss_tot.backward() # compute gradients
dis_optimizer.step() # update weights and biases
# 3c. train gen with fake images
gen_optimizer.zero_grad()
zz = T.normal(0.0, 1.0,
size=(bat_size, gen.inpt_dim)).to(device) # 20
fake_images = gen(zz)
dis_fake_oupt = dis(fake_images).reshape(-1)
gen_loss = loss_func(dis_fake_oupt, all_ones)
gen_accum_loss += gen_loss
gen_loss.backward()
gen_optimizer.step()
if epoch % ep_log_interval == 0:
acc_dis = Accuracy(gen, dis, 500, verbose=False)
print(" epoch: %4d | dis loss: %0.4f | gen loss: %0.4f
| dis accuracy: %0.4f "
% (epoch, dis_accum_loss, gen_accum_loss, acc_dis))
print("Training complete ")
# -----------------------------------------------------------
# 4. TODO: save trained model
# 5. use generator to make fake images
gen.eval() # set mode
for i in range(1): # just 1 image for demo
rinpt = T.randn(1, gen.inpt_dim).to(device) # wrap normal()
with T.no_grad():
fi = gen(rinpt).numpy() # make image, convert to numpy
fi = np.rint(fi * 16)
print("nSynthetic generated image (de-normed): ")
print(fi)
display_digit(fi)
# -----------------------------------------------------------
if __name__ == "__main__":
main()
