
Antes de la introducción del modelo Transformer, las arquitecturas de codificador-decodificador basadas en RNN estaban implementando el uso de la atención para la traducción automática neuronal. El modelo Transformer revolucionó la implementación de la atención al dispensar la recurrencia y las convoluciones y, alternativamente, confiando únicamente en un mecanismo de auto-atención.
Primero nos centraremos en el mecanismo de atención de Transformer en este tutorial, y luego revisaremos el modelo de Transformer en otro.
En este tutorial, descubrirá el mecanismo de atención de Transformer para la traducción automática neuronal.
Después de completar este tutorial, sabrá:
- En qué se diferenciaba la atención del Transformer de la de sus predecesores.
- Cómo el transformador calcula la atención de un producto de puntos escalados.
- Cómo el Transformer calcula la atención de varios cabezales.
Empecemos.

El mecanismo de atención del transformador
Foto de Andreas Gücklhorn, algunos derechos reservados.
Descripción general del tutorial
Este tutorial se divide en dos partes; son:
- Introducción a la atención del transformador
- La atención del transformador
- Atención de productos de puntos escalados
- Atención multicabezal
Prerrequisitos
Para este tutorial, asumimos que ya está familiarizado con:
Introducción a la atención del transformador
Hasta ahora, nos hemos familiarizado con el uso de un mecanismo de atención junto con una arquitectura codificadora-decodificadora basada en RNN. Hemos visto que dos de los modelos más populares que implementan la atención de esta manera han sido los propuestos por Bahdanau et al. (2014) y Luong et al. (2015).
La arquitectura Transformer revolucionó el uso de la atención al dispensar la recurrencia y las convoluciones, en las que los formadores habían confiado ampliamente.
… El Transformer es el primer modelo de transducción que se basa completamente en la auto-atención para calcular representaciones de su entrada y salida sin usar RNN alineados en secuencia o convolución.
– Atención es todo lo que necesita, 2017.
En su artículo, Atención es todo lo que necesita, Vaswani et al. (2017) explican que el modelo Transformer, alternativamente, se basa únicamente en el uso de la auto-atención, donde la representación de una secuencia (u oración) se calcula relacionando diferentes palabras en la misma secuencia.
La auto-atención, a veces llamada intra-atención, es un mecanismo de atención que relaciona diferentes posiciones de una sola secuencia para calcular una representación de la secuencia.
– Atención es todo lo que necesita, 2017.
La atención del transformador
Los principales componentes que utiliza Transformer atención son los siguientes:
- $ mathbf {q} $ y $ mathbf {k} $ que denotan vectores de dimensión, $ d_k $, que contienen las consultas y las claves, respectivamente.
- $ mathbf {v} $ que denota un vector de dimensión, $ d_v $, que contiene los valores.
- $ mathbf {Q} $, $ mathbf {K} $ y $ mathbf {V} $ denotan matrices que empaquetan conjuntos de consultas, claves y valores, respectivamente.
- $ mathbf {W} ^ Q $, $ mathbf {W} ^ K $ y $ mathbf {W} ^ V $ que denotan matrices de proyección que se utilizan para generar diferentes representaciones subespaciales de las matrices de consulta, clave y valor.
- $ mathbf {W} ^ O $ que denota una matriz de proyección para la salida de múltiples cabezales.
En esencia, la función de atención se puede considerar como un mapeo entre una consulta y un conjunto de pares clave-valor, a una salida.
La salida se calcula como una suma ponderada de los valores, donde el peso asignado a cada valor se calcula mediante una función de compatibilidad de la consulta con la clave correspondiente.
– Atención es todo lo que necesita, 2017.
Vaswani y col. proponer un atención escalada del producto escaladoy luego construir sobre él para proponer atención de múltiples cabezas. En el contexto de la traducción automática neuronal, la consulta, las claves y los valores que se utilizan como entradas a estos mecanismos de atención son proyecciones diferentes de la misma frase de entrada.
De manera intuitiva, por lo tanto, los mecanismos de atención propuestos implementan la auto-atención al capturar las relaciones entre los diferentes elementos (en este caso, las palabras) de una misma oración.
Atención de productos escalados
El Transformer implementa una atención de producto escalado, que sigue el procedimiento del mecanismo de atención general que habíamos visto anteriormente.
Como sugiere el nombre, la atención escalada del producto escalado primero calcula un producto escalar para cada consulta, $ mathbf {q} $, con todas las claves, $ mathbf {k} $. Posteriormente, divide cada resultado por $ sqrt {d_k} $ y procede a aplicar una función softmax. Al hacerlo, obtiene los pesos que se utilizan para escala los valores, $ mathbf {v} $.
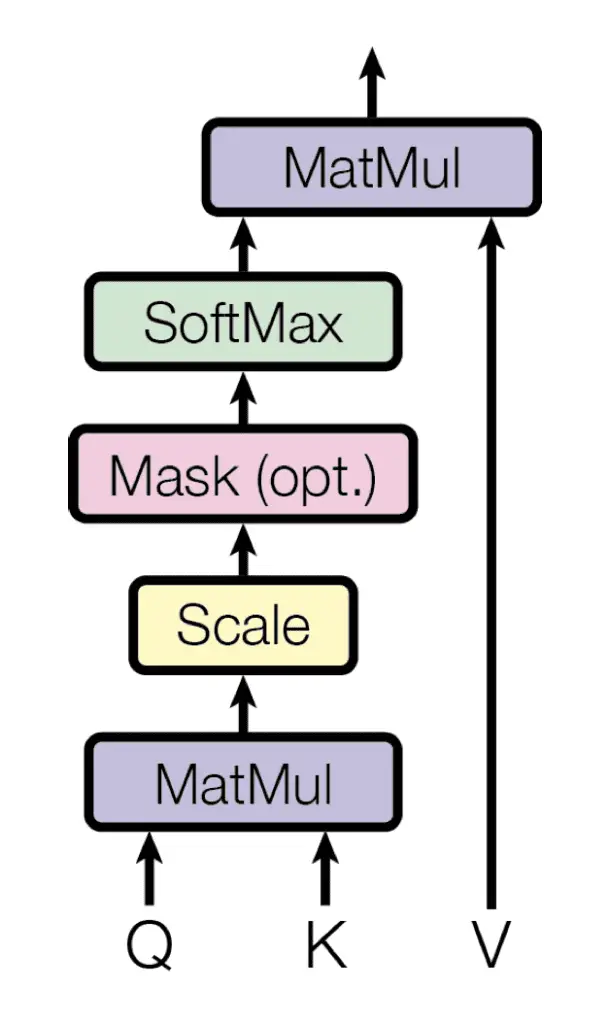
Atención de productos escalados
Tomado de «Atención es todo lo que necesita»
En la práctica, los cálculos realizados por la atención del producto punto escalado se pueden aplicar de manera eficiente en todo el conjunto de consultas simultáneamente. Para ello, las matrices $ mathbf {Q} $, $ mathbf {K} $ y $ mathbf {V} $, se suministran como entradas a la función de atención:
$$ text {atención} ( mathbf {Q}, mathbf {K}, mathbf {V}) = text {softmax} left ( frac {QK ^ T} { sqrt {d_k}} derecha) V $$
Vaswani y col. explican que su atención escalada al producto escalado es idéntica a la atención multiplicativa de Luong et al. (2015), excepto por el factor de escala agregado de $ tfrac {1} { sqrt {d_k}} $.
Este factor de escala se introdujo para contrarrestar el efecto de que los productos punto crezcan en magnitud para valores grandes de $ d_k $, donde la aplicación de la función softmax devolvería gradientes extremadamente pequeños que conducirían al infame problema de gradientes de desaparición. El factor de escala, por lo tanto, sirve para reducir los resultados generados por la multiplicación del producto escalar, evitando así este problema.
Vaswani y col. explicar además que su elección de optar por la atención multiplicativa en lugar de la atención aditiva de Bahdanau et al. (2014), se basó en la eficiencia computacional asociada al primero.
… La atención del producto punto es mucho más rápida y más eficiente en el espacio en la práctica, ya que se puede implementar utilizando un código de multiplicación de matrices altamente optimizado.
– Atención es todo lo que necesita, 2017.
El procedimiento paso a paso para calcular la atención del producto de puntos escalados es, por lo tanto, el siguiente:
- Calcule las puntuaciones de alineación multiplicando el conjunto de consultas empaquetadas en la matriz, $ mathbf {Q} $, con las claves en la matriz, $ mathbf {K} $. Si la matriz, $ mathbf {Q} $, es de tamaño $ m veces d_k $ y la matriz, $ mathbf {K} $, es de tamaño, $ n veces d_k $, entonces la matriz resultante será de tamaño $ m veces n $:
$$
mathbf {QK} ^ T =
begin {bmatrix}
e_ {11} & e_ {12} & dots & e_ {1n} \
e_ {21} & e_ {22} & dots & e_ {2n} \
vdots & vdots & ddots & vdots \
e_ {m1} & e_ {m2} & dots & e_ {mn} \
end {bmatrix}
$$
- Escale cada una de las puntuaciones de alineación en $ tfrac {1} { sqrt {d_k}} $:
$$
frac { mathbf {QK} ^ T} { sqrt {d_k}} =
begin {bmatrix}
tfrac {e_ {11}} { sqrt {d_k}} & tfrac {e_ {12}} { sqrt {d_k}} & dots & tfrac {e_ {1n}} { sqrt {d_k}} \
tfrac {e_ {21}} { sqrt {d_k}} & tfrac {e_ {22}} { sqrt {d_k}} & dots & tfrac {e_ {2n}} { sqrt {d_k}} \
vdots & vdots & ddots & vdots \
tfrac {e_ {m1}} { sqrt {d_k}} & tfrac {e_ {m2}} { sqrt {d_k}} & dots & tfrac {e_ {mn}} { sqrt {d_k}} \
end {bmatrix}
$$
- Y siga el proceso de escalado aplicando una operación softmax para obtener un conjunto de pesos:
$$
text {softmax} left ( frac { mathbf {QK} ^ T} { sqrt {d_k}} right) =
begin {bmatrix}
text {softmax} left ( tfrac {e_ {11}} { sqrt {d_k}} right) & text {softmax} left ( tfrac {e_ {12}} { sqrt {d_k}} right) & dots & text {softmax} left ( tfrac {e_ {1n}} { sqrt {d_k}} right) \
text {softmax} left ( tfrac {e_ {21}} { sqrt {d_k}} right) & text {softmax} left ( tfrac {e_ {22}} { sqrt {d_k}} right) & dots & text {softmax} left ( tfrac {e_ {2n}} { sqrt {d_k}} right) \
vdots & vdots & ddots & vdots \
text {softmax} left ( tfrac {e_ {m1}} { sqrt {d_k}} right) & text {softmax} left ( tfrac {e_ {m2}} { sqrt {d_k}} right) & dots & text {softmax} left ( tfrac {e_ {mn}} { sqrt {d_k}} right) \
end {bmatrix}
$$
- Finalmente, aplique los pesos resultantes a los valores en la matriz, $ mathbf {V} $, de tamaño, $ n times d_v $:
$$
begin {alineado}
& text {softmax} left ( frac { mathbf {QK} ^ T} { sqrt {d_k}} right) cdot mathbf {V} \
= &
begin {bmatrix}
text {softmax} left ( tfrac {e_ {11}} { sqrt {d_k}} right) & text {softmax} left ( tfrac {e_ {12}} { sqrt {d_k}} right) & dots & text {softmax} left ( tfrac {e_ {1n}} { sqrt {d_k}} right) \
text {softmax} left ( tfrac {e_ {21}} { sqrt {d_k}} right) & text {softmax} left ( tfrac {e_ {22}} { sqrt {d_k}} right) & dots & text {softmax} left ( tfrac {e_ {2n}} { sqrt {d_k}} right) \
vdots & vdots & ddots & vdots \
text {softmax} left ( tfrac {e_ {m1}} { sqrt {d_k}} right) & text {softmax} left ( tfrac {e_ {m2}} { sqrt {d_k}} right) & dots & text {softmax} left ( tfrac {e_ {mn}} { sqrt {d_k}} right) \
end {bmatrix}
cdot
begin {bmatrix}
v_ {11} & v_ {12} & dots & v_ {1d_v} \
v_ {21} & v_ {22} & dots & v_ {2d_v} \
vdots & vdots & ddots & vdots \
v_ {n1} & v_ {n2} & dots & v_ {nd_v} \
end {bmatrix}
end {alineado}
$$
Atención multicabezal
Basándose en su función de atención única que toma matrices, $ mathbf {Q} $, $ mathbf {K} $ y $ mathbf {V} $, como entrada, como acabamos de revisar, Vaswani et al. También proponen un mecanismo de atención multicabezal.
Su mecanismo de atención de múltiples cabezales proyecta linealmente las consultas, claves y valores $ h $ veces, cada vez utilizando una proyección aprendida diferente. El mecanismo de atención única se aplica luego a cada una de estas proyecciones $ h $ en paralelo, para producir salidas de $ h $, que a su vez se concatenan y proyectan nuevamente para producir un resultado final.
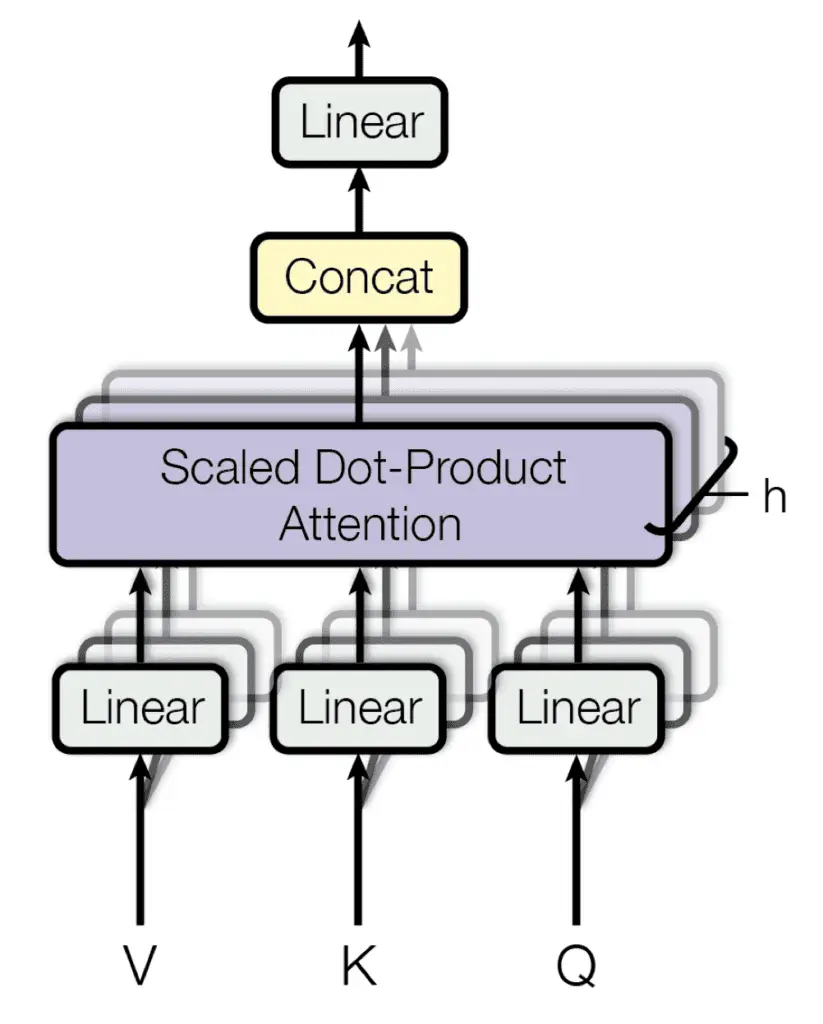
Atención multicabezal
Tomado de «Atención es todo lo que necesita»
La idea detrás de la atención de múltiples cabezas es permitir que la función de atención extraiga información de diferentes subespacios de representación, lo que, de otro modo, no sería posible con una sola cabeza de atención.
La función de atención de múltiples cabezales se puede representar de la siguiente manera:
$$ text {multihead} ( mathbf {Q}, mathbf {K}, mathbf {V}) = text {concat} ( text {head} _1, dots, text {head} _h) mathbf {W} ^ O $$
Aquí, cada $ text {head} _i $, $ i = 1, dots, h $, implementa una única función de atención caracterizada por sus propias matrices de proyección aprendidas:
$$ text {head} _i = text {atención} ( mathbf {QW} ^ Q_i, mathbf {KW} ^ K_i, mathbf {VW} ^ V_i) $$
El procedimiento paso a paso para calcular la atención de múltiples cabezales es, por lo tanto, el siguiente:
- Calcule las versiones proyectadas linealmente de las consultas, claves y valores mediante una multiplicación con las respectivas matrices de peso, $ mathbf {W} ^ Q_i $, $ mathbf {W} ^ K_i $ y $ mathbf {W} ^ V_i $ , uno por cada $ text {head} _i $.
- Aplique la función de atención única para cada cabeza (1) multiplicando las matrices de consultas y claves, (2) aplicando las operaciones de escala y softmax, y (3) ponderando la matriz de valores, para generar una salida para cada cabeza.
- Concatenar las salidas de las cabezas, $ text {head} _i $, $ i = 1, dots, h $.
- Aplique una proyección lineal a la salida concatenada mediante una multiplicación con la matriz de peso, $ mathbf {W} ^ O $, para generar el resultado final.
Otras lecturas
Esta sección proporciona más recursos sobre el tema si desea profundizar.
Libros
Documentos
Resumen
En este tutorial, descubrió el mecanismo de atención Transformer para la traducción automática neuronal.
Específicamente, aprendiste:
- En qué se diferenciaba la atención del Transformer de la de sus predecesores.
- Cómo el transformador calcula la atención de un producto de puntos escalados.
- Cómo el Transformer calcula la atención de varios cabezales.
¿Tiene usted alguna pregunta?
Haga sus preguntas en los comentarios a continuación y haré todo lo posible para responder.
