Puede resultar complicado desarrollar un modelo predictivo de red neuronal para un nuevo conjunto de datos.
Un enfoque es inspeccionar primero el conjunto de datos y desarrollar ideas sobre qué modelos podrían funcionar, luego explorar la dinámica de aprendizaje de modelos simples en el conjunto de datos y, finalmente, desarrollar y ajustar un modelo para el conjunto de datos con un arnés de prueba robusto.
Este proceso se puede utilizar para desarrollar modelos de redes neuronales efectivos para problemas de modelado predictivo de clasificación y regresión.
En este tutorial, descubrirá cómo desarrollar un modelo de red neuronal de perceptrón multicapa para el conjunto de datos de clasificación binaria de supervivencia del cáncer.
Después de completar este tutorial, sabrá:
- Cómo cargar y resumir el conjunto de datos de supervivencia del cáncer y usar los resultados para sugerir preparaciones de datos y configuraciones de modelos para usar.
- Cómo explorar la dinámica de aprendizaje de modelos MLP simples en el conjunto de datos.
- Cómo desarrollar estimaciones sólidas del rendimiento del modelo, ajustar el rendimiento del modelo y hacer predicciones sobre nuevos datos.
Empecemos.

Desarrollar una red neuronal para el conjunto de datos de supervivencia al cáncer
Foto de Bernd Thaller, algunos derechos reservados.
Descripción general del tutorial
Este tutorial se divide en 4 partes; ellos son:
- Conjunto de datos de supervivencia al cáncer de mama de Haberman
- Dinámica de aprendizaje de redes neuronales
- Evaluación robusta del modelo
- Modelo final y hacer predicciones
Conjunto de datos de supervivencia al cáncer de mama de Haberman
El primer paso es definir y explorar el conjunto de datos.
Trabajaremos con el «haberman”Conjunto de datos de clasificación binaria estándar.
El conjunto de datos describe los datos de los pacientes con cáncer de mama y el resultado es la supervivencia del paciente. Específicamente si el paciente sobrevivió durante cinco años o más, o si el paciente no sobrevivió.
Este es un conjunto de datos estándar que se utiliza en el estudio de la clasificación desequilibrada. Según la descripción del conjunto de datos, las operaciones se llevaron a cabo entre 1958 y 1970 en el Hospital Billings de la Universidad de Chicago.
Hay 306 ejemplos en el conjunto de datos y hay 3 variables de entrada; ellos son:
- La edad del paciente en el momento de la operación.
- El año de dos dígitos de la operación.
- El número de «ganglios axilares positivos”Detectado, una medida de si el cáncer se ha diseminado.
Como tal, no tenemos control sobre la selección de casos que componen el conjunto de datos o las características que se utilizarán en esos casos, aparte de lo que está disponible en el conjunto de datos.
Aunque el conjunto de datos describe la supervivencia de las pacientes con cáncer de mama, dado el pequeño tamaño del conjunto de datos y el hecho de que los datos se basan en el diagnóstico y las operaciones de cáncer de mama de hace muchas décadas, no se espera que los modelos creados en este conjunto de datos se generalicen.
Nota: para ser claro como el cristal, somos NO «resolviendo el cáncer de mama“. Estamos explorando un conjunto de datos de clasificación estándar.
A continuación se muestra una muestra de las primeras 5 filas del conjunto de datos
|
30,64,1,1 30,62,3,1 30,65,0,1 31,59,2,1 31,65,4,1 … |
Puede obtener más información sobre el conjunto de datos aquí:
Podemos cargar el conjunto de datos como un DataFrame de pandas directamente desde la URL; por ejemplo:
|
# cargar el conjunto de datos de haberman y resumir la forma de pandas importar leer_csv # definir la ubicación del conjunto de datos url = ‘https://raw.githubusercontent.com/jbrownlee/Datasets/master/haberman.csv’ # cargar el conjunto de datos df = read_csv(url, encabezamiento=Ninguno) # resumir forma impresión(df.forma) |
Al ejecutar el ejemplo, se carga el conjunto de datos directamente desde la URL e informa la forma del conjunto de datos.
En este caso, podemos confirmar que el conjunto de datos tiene 4 variables (3 entradas y una salida) y que el conjunto de datos tiene 306 filas de datos.
No se trata de muchas filas de datos para una red neuronal y sugiere que una red pequeña, quizás con regularización, sería apropiada.
También sugiere que el uso de la validación cruzada de k-fold sería una buena idea dado que dará una estimación más confiable del rendimiento del modelo que una división de tren / prueba y porque un solo modelo encajará en segundos en lugar de horas o días con el conjuntos de datos más grandes.
A continuación, podemos obtener más información sobre el conjunto de datos observando estadísticas resumidas y una gráfica de los datos.
|
# mostrar estadísticas resumidas y gráficos del conjunto de datos de haberman de pandas importar read_csv de matplotlib importar pyplot # definir la ubicación del conjunto de datos url = ‘https://raw.githubusercontent.com/jbrownlee/Datasets/master/haberman.csv’ # cargar el conjunto de datos df = read_csv(url, encabezamiento=Ninguno) # mostrar estadísticas resumidas impresión(df.describir()) # trazar histogramas df.hist() pyplot.show() |
Ejecutar el ejemplo primero carga los datos antes y luego imprime estadísticas de resumen para cada variable.
Podemos ver que los valores varían con diferentes medias y desviaciones estándar, quizás se requiera alguna normalización o estandarización antes del modelado.
|
0 1 2 3 recuento 306.000000 306.000000 306.000000 306.000000 media 52.457516 62.852941 4.026144 1.264706 estándar 10.803452 3.249405 7.189654 0.441899 min 30.000000 58.000000 0.000000 1.000000 25% 44,000000 60,000000 0,000000 1,000000 50% 52.000000 63.000000 1.000000 1.000000 75% 60.750000 65.750000 4.000000 2.000000 máx 83.000000 69.000000 52.000000 2.000000 |
Luego se crea un gráfico de histograma para cada variable.
Podemos ver que quizás la primera variable tiene una distribución similar a la de Gauss y las dos siguientes variables de entrada pueden tener una distribución exponencial.
Es posible que tengamos algún beneficio al usar una transformada de potencia en cada variable para hacer que la distribución de probabilidad sea menos sesgada, lo que probablemente mejorará el rendimiento del modelo.
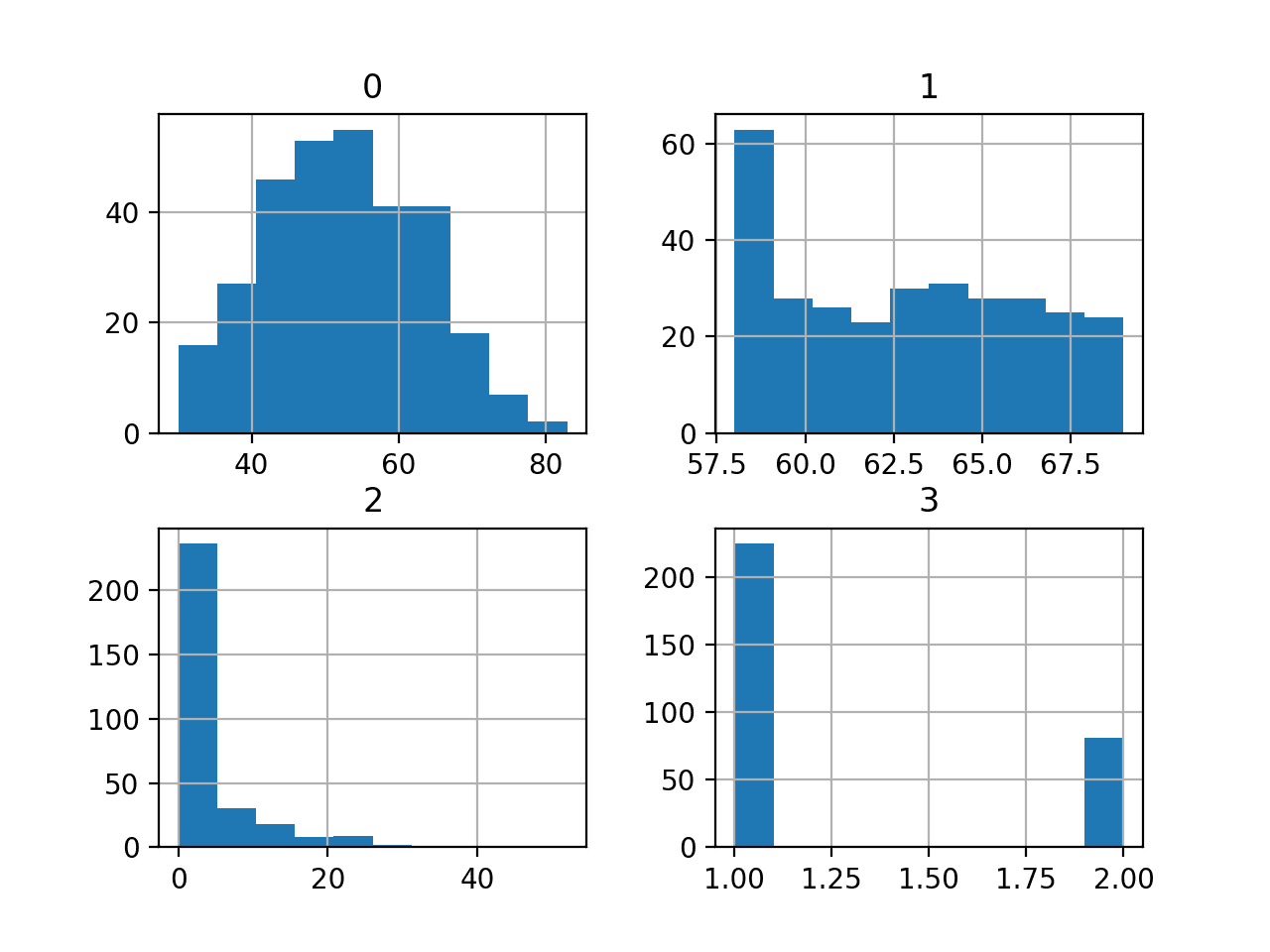
Histogramas del conjunto de datos de clasificación de supervivencia al cáncer de mama de Haberman
Podemos ver cierta desviación en la distribución de ejemplos entre las dos clases, lo que significa que el problema de clasificación no está equilibrado. Está desequilibrado.
Puede ser útil saber qué tan desequilibrado está realmente el conjunto de datos.
Podemos usar el objeto Contador para contar el número de ejemplos en cada clase, luego usar esos conteos para resumir la distribución.
El ejemplo completo se enumera a continuación.
|
# resumir la relación de clases del conjunto de datos de haberman de pandas importar read_csv de colecciones importar Encimera # definir la ubicación del conjunto de datos url = ‘https://raw.githubusercontent.com/jbrownlee/Datasets/master/haberman.csv’ # definir los nombres de las columnas del conjunto de datos columnas = [[‘edad’, ‘año’, ‘nodos’, ‘clase’] # cargue el archivo csv como un marco de datos marco de datos = read_csv(url, encabezamiento=Ninguno, nombres=columnas) # resumir la distribución de clases objetivo = marco de datos[[‘clase’].valores encimera = Encimera(objetivo) por k,v en encimera.artículos(): por = v / len(objetivo) * 100 impresión(‘Clase =% d, Recuento =% d, Porcentaje =%. 3f %%’ % (k, v, por)) |
La ejecución del ejemplo resume la distribución de clases del conjunto de datos.
Podemos ver que la clase 1 para supervivencia tiene la mayor cantidad de ejemplos en 225, o alrededor del 74 por ciento del conjunto de datos. Podemos ver que la clase 2 de no supervivencia tiene menos ejemplos en 81, o alrededor del 26 por ciento del conjunto de datos.
La distribución de clases está sesgada, pero no está muy desequilibrada.
|
Clase = 1, Recuento = 225, Porcentaje = 73,529% Clase = 2, Recuento = 81, Porcentaje = 26,471% |
Esto es útil porque si usamos la precisión de clasificación, cualquier modelo que logre una precisión menor a aproximadamente el 73,5% no tiene habilidad en este conjunto de datos.
Ahora que estamos familiarizados con el conjunto de datos, exploremos cómo podríamos desarrollar un modelo de red neuronal.
Dinámica de aprendizaje de redes neuronales
Desarrollaremos un modelo de perceptrón multicapa (MLP) para el conjunto de datos utilizando TensorFlow.
No podemos saber qué modelo de arquitectura de hiperparámetros de aprendizaje sería bueno o mejor para este conjunto de datos, por lo que debemos experimentar y descubrir qué funciona bien.
Dado que el conjunto de datos es pequeño, un tamaño de lote pequeño probablemente sea una buena idea, p. Ej. 16 o 32 filas. Usar la versión de Adam del descenso de gradiente estocástico es una buena idea al comenzar, ya que adaptará automáticamente la tasa de aprendizaje y funciona bien en la mayoría de los conjuntos de datos.
Antes de evaluar los modelos en serio, es una buena idea revisar la dinámica de aprendizaje y ajustar la arquitectura del modelo y la configuración de aprendizaje hasta que tengamos una dinámica de aprendizaje estable, luego buscar sacar el máximo provecho del modelo.
Podemos hacer esto usando una división simple de tren / prueba de los datos y revisar los gráficos de las curvas de aprendizaje. Esto nos ayudará a ver si estamos aprendiendo demasiado o mal; entonces podemos adaptar la configuración en consecuencia.
Primero, debemos asegurarnos de que todas las variables de entrada sean valores de punto flotante y codificar la etiqueta de destino como valores enteros 0 y 1.
|
... # asegúrese de que todos los datos sean valores de punto flotante X = X.astipo(‘float32’) # codificar cadenas a números enteros y = LabelEncoder().fit_transform(y) |
A continuación, podemos dividir el conjunto de datos en variables de entrada y salida, luego en conjuntos de prueba y tren 67/33.
Debemos asegurarnos de que la división esté estratificada por clase, asegurándonos de que el tren y los conjuntos de prueba tengan la misma distribución de etiquetas de clase que el conjunto de datos principal.
|
... # dividir en columnas de entrada y salida X, y = df.valores[[:, :–1], df.valores[[:, –1] # dividir en conjuntos de datos de prueba y de tren X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0,5, estratificar=y, estado_aleatorio=3) |
Podemos definir un modelo MLP mínimo. En este caso, usaremos una capa oculta con 10 nodos y una capa de salida (elegida arbitrariamente). Usaremos la función de activación de ReLU en la capa oculta y el «él_normal”Inicialización de peso, ya que juntos, son una buena práctica.
La salida del modelo es una activación sigmoidea para la clasificación binaria y minimizaremos la pérdida de entropía cruzada binaria.
|
... # determinar el número de características de entrada n_features = X.forma[[1] # definir modelo modelo = Secuencial() modelo.agregar(Denso(10, activación=‘relu’, kernel_initializer=‘él_normal’, input_shape=(n_features,))) modelo.agregar(Denso(1, activación=‘sigmoideo’)) # compilar el modelo modelo.compilar(optimizador=‘Adán’, pérdida=‘binary_crossentropy’) |
Ajustaremos el modelo para 200 épocas de entrenamiento (elegidas arbitrariamente) con un tamaño de lote de 16 porque es un conjunto de datos pequeño.
Estamos ajustando el modelo a datos sin procesar, lo que creemos que podría ser una buena idea, pero es un punto de partida importante.
|
... # encajar en el modelo historia = modelo.encajar(X_train, y_train, épocas=200, tamaño del lote=dieciséis, verboso=0, validation_data=(X_test,y_test)) |
Al final del entrenamiento, evaluaremos el desempeño del modelo en el conjunto de datos de prueba y reportaremos el desempeño como la precisión de clasificación.
|
... # predecir el conjunto de pruebas yhat = modelo.predecir_clases(X_test) # evaluar predicciones puntaje = puntuación_de_precisión(y_test, yhat) impresión(‘Precisión:% .3f’ % puntaje) |
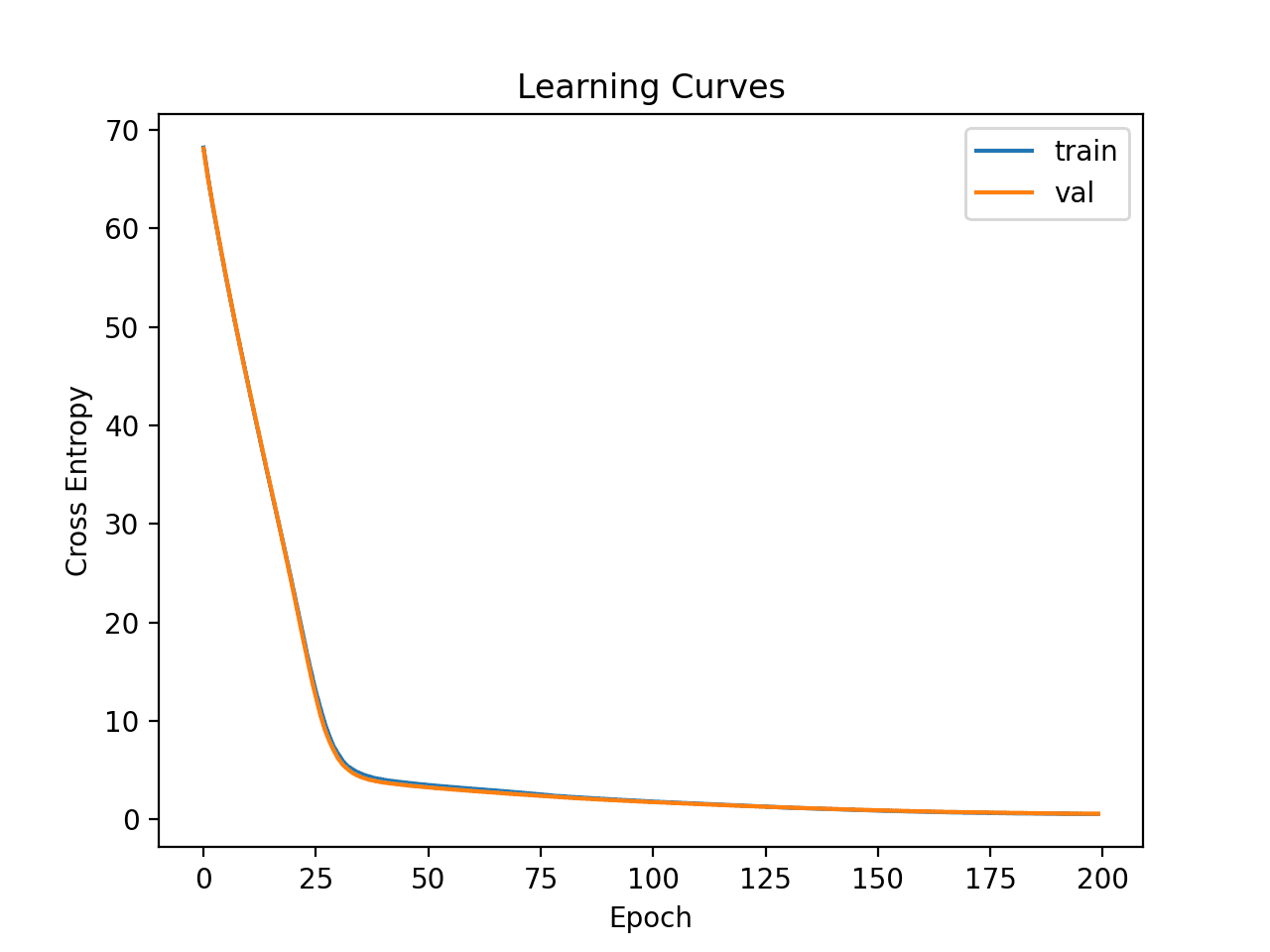
Finalmente, trazaremos las curvas de aprendizaje de la pérdida de entropía cruzada en el tren y los conjuntos de prueba durante el entrenamiento.
|
... # trazar curvas de aprendizaje pyplot.título(‘Curvas de aprendizaje’) pyplot.xlabel(‘Época’) pyplot.etiqueta(‘Entropía cruzada’) pyplot.gráfico(historia.historia[[‘pérdida’], etiqueta=‘entrenar’) pyplot.gráfico(historia.historia[[‘val_loss’], etiqueta=‘val’) pyplot.leyenda() pyplot.show() |
Uniendo todo esto, el ejemplo completo de la evaluación de nuestro primer MLP en el conjunto de datos de supervivencia del cáncer se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
# ajuste un modelo mlp simple en el haberman y revise las curvas de aprendizaje de pandas importar read_csv de sklearn.model_selection importar train_test_split de sklearn.preprocesamiento importar LabelEncoder de sklearn.métrica importar puntuación_de_precisión de tensorflow.keras importar Secuencial de tensorflow.keras.capas importar Denso de matplotlib importar pyplot # cargar el conjunto de datos camino = ‘https://raw.githubusercontent.com/jbrownlee/Datasets/master/haberman.csv’ df = read_csv(camino, encabezamiento=Ninguno) # dividir en columnas de entrada y salida X, y = df.valores[[:, :–1], df.valores[[:, –1] # asegúrese de que todos los datos sean valores de punto flotante X = X.astipo(‘float32’) # codificar cadenas a números enteros y = LabelEncoder().fit_transform(y) # dividir en conjuntos de datos de prueba y de tren X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0,5, estratificar=y, estado_aleatorio=3) # determinar el número de características de entrada n_features = X.forma[[1] # definir modelo modelo = Secuencial() modelo.agregar(Denso(10, activación=‘relu’, kernel_initializer=‘él_normal’, input_shape=(n_features,))) modelo.agregar(Denso(1, activación=‘sigmoideo’)) # compilar el modelo modelo.compilar(optimizador=‘Adán’, pérdida=‘binary_crossentropy’) # encajar en el modelo historia = modelo.encajar(X_train, y_train, épocas=200, tamaño del lote=dieciséis, verboso=0, validation_data=(X_test,y_test)) # predecir el conjunto de pruebas yhat = modelo.predecir_clases(X_test) # evaluar predicciones puntaje = puntuación_de_precisión(y_test, yhat) impresión(‘Precisión:% .3f’ % puntaje) # trazar curvas de aprendizaje pyplot.título(‘Curvas de aprendizaje’) pyplot.xlabel(‘Época’) pyplot.etiqueta(‘Entropía cruzada’) pyplot.gráfico(historia.historia[[‘pérdida’], etiqueta=‘entrenar’) pyplot.gráfico(historia.historia[[‘val_loss’], etiqueta=‘val’) pyplot.leyenda() pyplot.show() |
Ejecutar el ejemplo primero ajusta el modelo en el conjunto de datos de entrenamiento, luego informa la precisión de la clasificación en el conjunto de datos de prueba.
Pon en marcha tu proyecto con mi nuevo libro Preparación de datos para el aprendizaje automático, que incluye tutoriales paso a paso y el Código fuente de Python archivos para todos los ejemplos.
En este caso, podemos ver que el modelo funciona mejor que un modelo sin habilidad, dado que la precisión está por encima del 73,5%.
A continuación, se crean los gráficos de línea de la pérdida en el tren y los conjuntos de prueba.
Podemos ver que el modelo encuentra rápidamente un buen ajuste en el conjunto de datos y no parece estar sobreajustado o desajustado.

Curvas de aprendizaje del perceptrón multicapa simple en el conjunto de datos de supervivencia al cáncer
Ahora que tenemos una idea de la dinámica de aprendizaje para un modelo MLP simple en el conjunto de datos, podemos considerar el desarrollo de una evaluación más sólida del desempeño del modelo en el conjunto de datos.
Evaluación robusta del modelo
El procedimiento de validación cruzada de k veces puede proporcionar una estimación más confiable del rendimiento de MLP, aunque puede ser muy lento.
Esto se debe a que los modelos k deben ajustarse y evaluarse. Esto no es un problema cuando el tamaño del conjunto de datos es pequeño, como el conjunto de datos de supervivencia al cáncer.
Podemos usar la clase StratifiedKFold y enumerar cada pliegue manualmente, ajustar el modelo, evaluarlo y luego informar la media de las puntuaciones de evaluación al final del procedimiento.
|
... # preparar la validación cruzada kfold = KFold(10) # enumerar divisiones puntuaciones = lista() por train_ix, test_ix en kfold.separar(X, y): # ajustar y evaluar el modelo … ... ... # resumir todas las puntuaciones impresión(‘Precisión media:% .3f (% .3f)’ % (significar(puntuaciones), std(puntuaciones))) |
Podemos usar este marco para desarrollar una estimación confiable del rendimiento del modelo MLP con nuestra configuración base, e incluso con una variedad de diferentes preparaciones de datos, arquitecturas de modelos y configuraciones de aprendizaje.
Es importante que primero desarrollemos una comprensión de la dinámica de aprendizaje del modelo en el conjunto de datos en la sección anterior antes de usar la validación cruzada de k-veces para estimar el rendimiento. Si comenzamos a ajustar el modelo directamente, podríamos obtener buenos resultados, pero si no, es posible que no tengamos idea de por qué, p. que el modelo se ajustaba demasiado o no.
Si volvemos a realizar cambios importantes en el modelo, es una buena idea volver atrás y confirmar que el modelo está convergiendo adecuadamente.
El ejemplo completo de este marco para evaluar el modelo MLP base de la sección anterior se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 |
# k-veces de validación cruzada del modelo base para el conjunto de datos de haberman de numpy importar significar de numpy importar std de pandas importar read_csv de sklearn.model_selection importar Estratificado KFold de sklearn.preprocesamiento importar LabelEncoder de sklearn.métrica importar puntuación_de_precisión de tensorflow.keras importar Secuencial de tensorflow.keras.capas importar Denso de matplotlib importar pyplot # cargar el conjunto de datos camino = ‘https://raw.githubusercontent.com/jbrownlee/Datasets/master/haberman.csv’ df = read_csv(camino, encabezamiento=Ninguno) # dividir en columnas de entrada y salida X, y = df.valores[[:, :–1], df.valores[[:, –1] # ensure all data are floating point values X = X.astype(‘float32’) # encode strings to integer y = LabelEncoder().fit_transform(y) # prepare cross validation kfold = StratifiedKFold(10, random_state=1) # enumerate splits scores = list() for train_ix, test_ix en kfold.split(X, y): # split data X_train, X_test, y_train, y_test = X[[train_ix], X[[test_ix], y[[train_ix], y[[test_ix] # determine the number of input features n_features = X.shape[[1] # define model model = Sequential() model.add(Dense(10, activation=‘relu’, kernel_initializer=‘he_normal’, input_shape=(n_features,))) model.add(Dense(1, activation=‘sigmoid’)) # compile the model model.compile(optimizer=‘adam’, loss=‘binary_crossentropy’) # fit the model model.fit(X_train, y_train, epochs=200, batch_size=dieciséis, verbose=0) # predict test set yhat = model.predict_classes(X_test) # evaluate predictions score = accuracy_score(y_test, yhat) print(‘>%.3f’ % score) scores.append(score) # summarize all scores print(‘Mean Accuracy: %.3f (%.3f)’ % (mean(scores), std(scores))) |
Running the example reports the model performance each iteration of the evaluation procedure and reports the mean and standard deviation of classification accuracy at the end of the run.
Kick-start your project with my new book Data Preparation for Machine Learning, including step-by-step tutorials and the Python source code files for all examples.
In this case, we can see that the MLP model achieved a mean accuracy of about 75.2 percent, which is pretty close to our rough estimate in the previous section.
This confirms our expectation that the base model configuration may work better than a naive model for this dataset
|
>0.742 >0.774 >0.774 >0.806 >0.742 >0.710 >0.767 >0.800 >0.767 >0.633 Mean Accuracy: 0.752 (0.048) |
Is this a good result?
In fact, this is a challenging classification problem and achieving a score above about 74.5% is good.
Next, let’s look at how we might fit a final model and use it to make predictions.
Final Model and Make Predictions
Once we choose a model configuration, we can train a final model on all available data and use it to make predictions on new data.
In this case, we will use the model with dropout and a small batch size as our final model.
We can prepare the data and fit the model as before, although on the entire dataset instead of a training subset of the dataset.
|
... # split into input and output columns X, y = df.values[[:, :–1], df.values[[:, –1] # ensure all data are floating point values X = X.astype(‘float32’) # encode strings to integer le = LabelEncoder() y = le.fit_transform(y) # determine the number of input features n_features = X.shape[[1] # define model model = Sequential() model.add(Dense(10, activation=‘relu’, kernel_initializer=‘he_normal’, input_shape=(n_features,))) model.add(Dense(1, activation=‘sigmoid’)) # compile the model model.compile(optimizer=‘adam’, loss=‘binary_crossentropy’) |
We can then use this model to make predictions on new data.
First, we can define a row of new data.
|
... # define a row of new data row = [[30,64,1] |
Note: I took this row from the first row of the dataset and the expected label is a ‘1’.
We can then make a prediction.
|
... # make prediction yhat = model.predict_classes([[row]) |
Then invert the transform on the prediction, so we can use or interpret the result in the correct label (which is just an integer for this dataset).
|
... # invert transform to get label for class yhat = le.inverse_transform(yhat) |
And in this case, we will simply report the prediction.
|
... # report prediction print(‘Predicted: %s’ % (yhat[[0])) |
Tying this all together, the complete example of fitting a final model for the haberman dataset and using it to make a prediction on new data is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
# fit a final model and make predictions on new data for the haberman dataset de pandas import read_csv de sklearn.preprocessing import LabelEncoder de sklearn.metrics import accuracy_score de tensorflow.keras import Sequential de tensorflow.keras.layers import Dense de tensorflow.keras.layers import Dropout # load the dataset path = ‘https://raw.githubusercontent.com/jbrownlee/Datasets/master/haberman.csv’ df = read_csv(path, header=None) # split into input and output columns X, y = df.values[[:, :–1], df.values[[:, –1] # ensure all data are floating point values X = X.astype(‘float32’) # encode strings to integer le = LabelEncoder() y = le.fit_transform(y) # determine the number of input features n_features = X.shape[[1] # define model model = Sequential() model.add(Dense(10, activation=‘relu’, kernel_initializer=‘he_normal’, input_shape=(n_features,))) model.add(Dense(1, activation=‘sigmoid’)) # compile the model model.compile(optimizer=‘adam’, loss=‘binary_crossentropy’) # fit the model model.fit(X, y, epochs=200, batch_size=dieciséis, verbose=0) # define a row of new data row = [[30,64,1] # make prediction yhat = model.predict_classes([[row]) # invert transform to get label for class yhat = le.inverse_transform(yhat) # report prediction print(‘Predicted: %s’ % (yhat[[0])) |
Running the example fits the model on the entire dataset and makes a prediction for a single row of new data.
Kick-start your project with my new book Data Preparation for Machine Learning, including step-by-step tutorials and the Python source code files for all examples.
In this case, we can see that the model predicted a “1” label for the input row.
Further Reading
This section provides more resources on the topic if you are looking to go deeper.
Tutorials
Resumen
In this tutorial, you discovered how to develop a Multilayer Perceptron neural network model for the cancer survival binary classification dataset.
Specifically, you learned:
- How to load and summarize the cancer survival dataset and use the results to suggest data preparations and model configurations to use.
- How to explore the learning dynamics of simple MLP models on the dataset.
- How to develop robust estimates of model performance, tune model performance and make predictions on new data.
Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.

