La agregación de Bootstrap, o embolsado, es un conjunto en el que cada modelo se entrena en una muestra diferente del conjunto de datos de entrenamiento.
La idea de embolsar puede generalizarse a otras técnicas para cambiar el conjunto de datos de entrenamiento y ajustar el mismo modelo en cada versión modificada de los datos. Un enfoque consiste en utilizar transformaciones de datos que cambian la escala y la distribución de probabilidad de las variables de entrada como base para el entrenamiento de los miembros que contribuyen a un conjunto similar al del embolsado. Podemos referirnos a esto como embolsamiento de transformación de datos o un conjunto de transformación de datos.
En este tutorial, descubrirá cómo desarrollar un conjunto de transformación de datos.
Después de completar este tutorial, lo sabrás:
- Las transformaciones de datos pueden utilizarse como base para un conjunto de tipo «bagging» en el que el mismo modelo se entrena en diferentes vistas de un conjunto de datos de entrenamiento.
- Cómo desarrollar un conjunto de transformación de datos para la clasificación y confirmar que el conjunto funciona mejor que cualquier miembro contribuyente.
- Cómo desarrollar y evaluar un conjunto de transformación de datos para el modelado predictivo de regresión.
Empecemos.

Desarrollar un conjunto de empaquetamiento con diferentes transformaciones de datos
Foto de Maciej Kraus, algunos derechos reservados.
Resumen del Tutorial
Este tutorial está dividido en tres partes; son:
- Transformación de datos en bolsas
- Conjunto de transformación de datos para la clasificación
- Conjunto de transformación de datos para la regresión
Transformación de datos en bolsas
La agregación de Bootstrap, o en forma abreviada, es una técnica de aprendizaje en conjunto basada en la idea de ajustar el mismo tipo de modelo en múltiples muestras diferentes del mismo conjunto de datos de entrenamiento.
Se espera que las pequeñas diferencias en el conjunto de datos de capacitación utilizados para ajustar cada modelo den lugar a pequeñas diferencias en las capacidades de los modelos. En el caso del aprendizaje en conjunto, esto se denomina diversidad de los miembros del conjunto y tiene por objeto descoordinar las predicciones (o errores de predicción) realizadas por cada miembro contribuyente.
Aunque se diseñó para ser utilizado con árboles de decisión y cada muestra de datos se hace utilizando el método bootstrap (selección con rel-selección), el enfoque ha generado todo un subcampo de estudio con cientos de variaciones en el enfoque.
Podemos construir nuestros propios grupos de empaquetamiento cambiando el conjunto de datos utilizados para entrenar a cada miembro contribuyente de maneras nuevas y únicas.
Un enfoque consistiría en aplicar una transformación de preparación de datos diferente al conjunto de datos de cada miembro del conjunto contribuyente.
Esto se basa en la premisa de que no podemos conocer la forma de representación de un conjunto de datos de entrenamiento que exponga la estructura subyacente desconocida del conjunto de datos a los algoritmos de aprendizaje. Esto motiva la necesidad de evaluar los modelos con un conjunto de diferentes transformaciones de datos, como el cambio de escala y la distribución de probabilidad, para descubrir qué es lo que funciona.
Este enfoque puede utilizarse cuando se crea un conjunto de diferentes transformaciones del mismo conjunto de datos de entrenamiento, un modelo entrenado en cada una de ellas, y las predicciones combinadas utilizando estadísticas simples como el promedio.
A falta de un nombre mejor, nos referiremos a esto como «Transformación de datos en bolsas«o un»Conjunto de transformación de datos.”
Hay muchas transformaciones que podemos utilizar, pero quizás un buen punto de partida sería una selección que cambie la escala y la distribución de probabilidad, como por ejemplo:
Es probable que el enfoque sea más eficaz cuando se utilice con un modelo base que entrene modelos diferentes o muy diferentes basados en los efectos de la transformación de los datos.
Cambiar la escala de la distribución puede ser apropiado sólo con modelos que sean sensibles a los cambios en la escala de las variables de entrada, como los que calculan una suma ponderada, como la regresión logística y las redes neuronales, y los que utilizan medidas de distancia, como los vecinos más cercanos y las máquinas de vectores de apoyo.
Los cambios en la distribución de probabilidad de las variables de entrada probablemente afectarán a la mayoría de los modelos de aprendizaje automático.
Ahora que estamos familiarizados con el enfoque, exploremos cómo podemos desarrollar un conjunto de transformación de datos para los problemas de clasificación.
Conjunto de transformación de datos para la clasificación
Podemos desarrollar un enfoque de transformación de datos para el embolsado para la clasificación usando la biblioteca de aprendizaje científico.
La biblioteca proporciona un conjunto de transformaciones estándar que podemos usar directamente. Cada miembro del conjunto puede definirse como una Pipeline, con la transformación seguida del modelo predictivo, para evitar cualquier fuga de datos y, a su vez, producir resultados optimistas. Por último, un conjunto de votación puede ser utilizado para combinar las predicciones de cada tubería.
En primer lugar, podemos definir un conjunto de datos de clasificación binaria sintética como base para explorar este tipo de conjunto.
En el ejemplo que figura a continuación se crea un conjunto de datos con 1.000 ejemplos, cada uno de los cuales comprende 20 características de entrada, en los que 15 de ellos contienen información para predecir el objetivo.
|
# Conjunto de datos de clasificación sintética de sklearn.conjuntos de datos importación hacer_clasificación # Definir el conjunto de datos X, y = make_classification(n_muestras=1000, n_funciones=20, n_informativo=15, n_redundante=5, estado_aleatorio=1) # resumir el conjunto de datos imprimir(X.forma, y.forma) |
Ejecutando el ejemplo se creará el conjunto de datos y se resumirá la forma de los conjuntos de datos, confirmando nuestras expectativas.
A continuación, establecemos una línea de base sobre el problema utilizando el modelo de predicción que pretendemos utilizar en nuestro conjunto. Es una práctica estándar utilizar un árbol de decisión en los conjuntos de bolsas, así que en este caso, utilizaremos el Clasificador de Árbol de Decisión con hiperparámetros por defecto.
Evaluaremos el modelo utilizando prácticas estándar, en este caso, la validación cruzada estratificada de tres repeticiones y 10 pliegues. El rendimiento se informará utilizando la media de la precisión de la clasificación en todos los pliegues y repeticiones.
El ejemplo completo de la evaluación de un árbol de decisión sobre el conjunto de datos de la clasificación sintética se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# Evaluar el árbol de decisiones sobre el conjunto de datos de clasificación sintética de numpy importación significa de numpy importación std de sklearn.conjuntos de datos importación make_classification de sklearn.model_selection importación puntaje_valor_cruzado de sklearn.model_selection importación RepeatedStratifiedKFold de sklearn.árbol importación DecisionTreeClassifier # Definir el conjunto de datos X, y = make_classification(n_muestras=1000, n_funciones=20, n_informativo=15, n_redundante=5, estado_aleatorio=1) # Definir el modelo modelo = DecisionTreeClassifier() # Definir el procedimiento de evaluación cv = RepeatedStratifiedKFold(n_splits=10, n_repeticiones=3, estado_aleatorio=1) # Evaluar el modelo n_puntuaciones = puntaje_valor_cruzado(modelo, X, y, puntuación=«exactitud, cv=cv, n_jobs=–1) # Informe de rendimiento imprimir(«Precisión media: %.3f (%.3f) % (significa(n_puntuaciones), std(n_puntuaciones))) |
La ejecución del ejemplo informa de la precisión de la clasificación media del árbol de decisión en el conjunto de datos de la clasificación sintética.
Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o el procedimiento de evaluación, o las diferencias en la precisión numérica. Considere ejecutar el ejemplo unas cuantas veces y compare el resultado promedio.
En este caso, podemos ver que el modelo alcanzó una precisión de clasificación de alrededor del 82,3 por ciento.
Esta puntuación proporciona una línea de base en el desempeño de la cual esperamos que un conjunto de transformación de datos mejore.
|
Precisión media: 0,823 (0,039) |
A continuación, podemos desarrollar un conjunto de árboles de decisión, cada uno de los cuales encaja en una transformación diferente de los datos de entrada.
Primero, podemos definir a cada miembro del conjunto como una tubería de modelado. El primer paso será la transformación de datos y el segundo será un clasificador de árbol de decisión.
Por ejemplo, la tubería para una transformación de normalización con la clase MinMaxScaler tendría el siguiente aspecto:
|
... # Normalización… norma = Oleoducto([[(‘s’, MinMaxScaler()), (‘m’, DecisionTreeClassifier())]) |
Podemos repetir esto para cada transformación o configuración de transformación que queramos usar y añadir todas las tuberías modelo a una lista.
La clase de VotingClassifier puede ser usada para combinar las predicciones de todos los modelos. Esta clase toma un «estimadoresEl argumento de «que es una lista de tuplas donde cada tupla tiene un nombre y el modelo o tubería de modelado. Por ejemplo:
|
... # Normalización… norma = Oleoducto([[(‘s’, MinMaxScaler()), (‘m’, DecisionTreeClassifier())]) modelos.anexar((«norma, norma)) ... # Definir el conjunto de votos conjunto = VotingClassifier(estimadores=modelos, votación=«duro) |
Para facilitar la lectura del código, podemos definir una función get_ensemble() para crear los miembros y los datos transforman el conjunto en sí mismo.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
# Obtener un conjunto de modelos votantes def get_ensemble(): # Definir los modelos de base modelos = lista() # Normalización… norma = Oleoducto([[(‘s’, MinMaxScaler()), (‘m’, DecisionTreeClassifier())]) modelos.anexar((«norma, norma)) # Estandarización std = Oleoducto([[(‘s’, StandardScaler()), (‘m’, DecisionTreeClassifier())]) modelos.anexar((«std, std)) # robusto robusto = Oleoducto([[(‘s’, RobustScaler()), (‘m’, DecisionTreeClassifier())]) modelos.anexar((«robusto, robusto)) # Poder poder = Oleoducto([[(‘s’, Transformador de potencia()), (‘m’, DecisionTreeClassifier())]) modelos.anexar((«poder, poder)) # Cuantilito quant = Oleoducto([[(‘s’, QuantileTransformer(n_quantiles=100, distribución_de_salida=«normal)), (‘m’, DecisionTreeClassifier())]) modelos.anexar((«quant, quant)) # kbins kbins = Oleoducto([[(‘s’, KBinsDiscretizador(n_bins=20, codificar=«ordinal)), (‘m’, DecisionTreeClassifier())]) modelos.anexar((«kbins, kbins)) # Definir el conjunto de votos conjunto = VotingClassifier(estimadores=modelos, votación=«duro) volver conjunto |
Podemos entonces llamar a esta función y evaluar el conjunto de votos como de costumbre, tal como hicimos con el árbol de decisiones de arriba.
A continuación se muestra el ejemplo completo.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 |
# Evaluar los datos transformar el conjunto de bolsas en un conjunto de datos de clasificación de numpy importación significa de numpy importación std de sklearn.conjuntos de datos importación make_classification de sklearn.model_selection importación puntaje_valor_cruzado de sklearn.model_selection importación RepeatedStratifiedKFold de sklearn.preprocesamiento importación MinMaxScaler de sklearn.preprocesamiento importación StandardScaler de sklearn.preprocesamiento importación RobustScaler de sklearn.preprocesamiento importación Transformador de potencia de sklearn.preprocesamiento importación QuantileTransformer de sklearn.preprocesamiento importación KBinsDiscretizador de sklearn.árbol importación DecisionTreeClassifier de sklearn.conjunto importación VotingClassifier de sklearn.tubería importación Oleoducto # Obtener un conjunto de modelos votantes def get_ensemble(): # Definir los modelos de base modelos = lista() # Normalización… norma = Oleoducto([[(‘s’, MinMaxScaler()), (‘m’, DecisionTreeClassifier())]) modelos.anexar((«norma, norma)) # Estandarización std = Oleoducto([[(‘s’, StandardScaler()), (‘m’, DecisionTreeClassifier())]) modelos.anexar((«std, std)) # robusto robusto = Oleoducto([[(‘s’, RobustScaler()), (‘m’, DecisionTreeClassifier())]) modelos.anexar((«robusto, robusto)) # Poder poder = Oleoducto([[(‘s’, Transformador de potencia()), (‘m’, DecisionTreeClassifier())]) modelos.anexar((«poder, poder)) # Cuantilito quant = Oleoducto([[(‘s’, QuantileTransformer(n_quantiles=100, distribución_de_salida=«normal)), (‘m’, DecisionTreeClassifier())]) modelos.anexar((«quant, quant)) # kbins kbins = Oleoducto([[(‘s’, KBinsDiscretizador(n_bins=20, codificar=«ordinal)), (‘m’, DecisionTreeClassifier())]) modelos.anexar((«kbins, kbins)) # Definir el conjunto de votos conjunto = VotingClassifier(estimadores=modelos, votación=«duro) volver conjunto # Definir el conjunto de datos X, y = make_classification(n_muestras=1000, n_funciones=20, n_informativo=15, n_redundante=5, estado_aleatorio=1) # Consigue modelos conjunto = get_ensemble() # Definir el procedimiento de evaluación cv = RepeatedStratifiedKFold(n_splits=10, n_repeticiones=3, estado_aleatorio=1) # Evaluar el modelo n_puntuaciones = puntaje_valor_cruzado(conjunto, X, y, puntuación=«exactitud, cv=cv, n_jobs=–1) # Informe de rendimiento imprimir(«Precisión media: %.3f (%.3f) % (significa(n_puntuaciones), std(n_puntuaciones))) |
La ejecución del ejemplo informa de la precisión de la clasificación media del conjunto de transformación de datos en el conjunto de datos de clasificación sintética.
Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o el procedimiento de evaluación, o las diferencias en la precisión numérica. Considere ejecutar el ejemplo unas cuantas veces y compare el resultado promedio.
En este caso, podemos ver que el conjunto de transformación de datos alcanzó una precisión de clasificación de alrededor del 83,8 por ciento, lo que supone un salto utilizando sólo un árbol de decisión que alcanzó una precisión de alrededor del 82,3 por ciento.
|
Precisión media: 0,838 (0,042) |
Aunque el conjunto funcionó bien en comparación con un árbol de decisión único, una limitación de esta prueba es que no sabemos si el conjunto funcionó mejor que cualquier miembro contribuyente.
Esto es importante, ya que si un miembro que contribuye al conjunto actúa mejor, entonces sería más sencillo y fácil utilizar el propio miembro como modelo en lugar del conjunto.
Podemos comprobarlo evaluando el rendimiento de cada modelo individual y comparando los resultados con el conjunto.
Primero, podemos actualizar el get_ensemble() para devolver una lista de modelos a evaluar compuesta por los miembros individuales del conjunto así como el conjunto mismo.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
# Obtener un conjunto de modelos votantes def get_ensemble(): # Definir los modelos de base modelos = lista() # Normalización… norma = Oleoducto([[(‘s’, MinMaxScaler()), (‘m’, DecisionTreeClassifier())]) modelos.anexar((«norma, norma)) # Estandarización std = Oleoducto([[(‘s’, StandardScaler()), (‘m’, DecisionTreeClassifier())]) modelos.anexar((«std, std)) # robusto robusto = Oleoducto([[(‘s’, RobustScaler()), (‘m’, DecisionTreeClassifier())]) modelos.anexar((«robusto, robusto)) # Poder poder = Oleoducto([[(‘s’, Transformador de potencia()), (‘m’, DecisionTreeClassifier())]) modelos.anexar((«poder, poder)) # Cuantilito quant = Oleoducto([[(‘s’, QuantileTransformer(n_quantiles=100, distribución_de_salida=«normal)), (‘m’, DecisionTreeClassifier())]) modelos.anexar((«quant, quant)) # kbins kbins = Oleoducto([[(‘s’, KBinsDiscretizador(n_bins=20, codificar=«ordinal)), (‘m’, DecisionTreeClassifier())]) modelos.anexar((«kbins, kbins)) # Definir el conjunto de votos conjunto = VotingClassifier(estimadores=modelos, votación=«duro) # Devuelve una lista de tuplas, cada una con un nombre y un modelo volver modelos + [[(«conjunto, conjunto)] |
Podemos llamar a esta función y enumerar cada modelo, evaluándolo, informando del rendimiento y almacenando los resultados.
|
... # Consigue modelos modelos = get_ensemble() # Evaluar cada modelo resultados = lista() para nombre,modelo en modelos: # Definir el método de evaluación cv = RepeatedStratifiedKFold(n_splits=10, n_repeticiones=3, estado_aleatorio=1) # Evaluar el modelo en el conjunto de datos n_puntuaciones = puntaje_valor_cruzado(modelo, X, y, puntuación=«exactitud, cv=cv, n_jobs=–1) # Informe de rendimiento imprimir(«>%s: %.3f (%.3f) % (nombre, significa(n_puntuaciones), std(n_puntuaciones))) resultados.anexar(n_puntuaciones) |
Finalmente, podemos trazar la distribución de las puntuaciones de precisión como gráficos de caja y bigote uno al lado del otro y comparar la distribución de las puntuaciones directamente.
Visualmente, esperaríamos que la distribución de las puntuaciones del conjunto se incline más que cualquier miembro individual y que la tendencia central de la distribución (media y mediana) sea también más alta que cualquier miembro.
|
... # Grafica los resultados para compararlos… pyplot.Boxplot(resultados, etiquetas=[[n para n,_ en modelos], showmeans=Verdadero) pyplot.mostrar() |
Enlazando todo esto, el ejemplo completo de la comparación del rendimiento de los miembros contribuyentes con el rendimiento del conjunto de transformación de datos se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 |
# Comparación de datos de transformación de conjunto a cada miembro contribuyente para su clasificación de numpy importación significa de numpy importación std de sklearn.conjuntos de datos importación make_classification de sklearn.model_selection importación puntaje_valor_cruzado de sklearn.model_selection importación RepeatedStratifiedKFold de sklearn.preprocesamiento importación MinMaxScaler de sklearn.preprocesamiento importación StandardScaler de sklearn.preprocesamiento importación RobustScaler de sklearn.preprocesamiento importación Transformador de potencia de sklearn.preprocesamiento importación QuantileTransformer de sklearn.preprocesamiento importación KBinsDiscretizador de sklearn.árbol importación DecisionTreeClassifier de sklearn.conjunto importación VotingClassifier de sklearn.tubería importación Oleoducto de matplotlib importación pyplot # Obtener un conjunto de modelos votantes def get_ensemble(): # Definir los modelos de base modelos = lista() # Normalización… norma = Oleoducto([[(‘s’, MinMaxScaler()), (‘m’, DecisionTreeClassifier())]) modelos.anexar((«norma, norma)) # Estandarización std = Oleoducto([[(‘s’, StandardScaler()), (‘m’, DecisionTreeClassifier())]) modelos.anexar((«std, std)) # robusto robusto = Oleoducto([[(‘s’, RobustScaler()), (‘m’, DecisionTreeClassifier())]) modelos.anexar((«robusto, robusto)) # Poder poder = Oleoducto([[(‘s’, Transformador de potencia()), (‘m’, DecisionTreeClassifier())]) modelos.anexar((«poder, poder)) # Cuantilito quant = Oleoducto([[(‘s’, QuantileTransformer(n_quantiles=100, distribución_de_salida=«normal)), (‘m’, DecisionTreeClassifier())]) modelos.anexar((«quant, quant)) # kbins kbins = Oleoducto([[(‘s’, KBinsDiscretizador(n_bins=20, codificar=«ordinal)), (‘m’, DecisionTreeClassifier())]) modelos.anexar((«kbins, kbins)) # Definir el conjunto de votos conjunto = VotingClassifier(estimadores=modelos, votación=«duro) # Devuelve una lista de tuplas, cada una con un nombre y un modelo volver modelos + [[(«conjunto, conjunto)] # Definir el conjunto de datos X, y = make_classification(n_muestras=1000, n_funciones=20, n_informativo=15, n_redundante=5, estado_aleatorio=1) # Consigue modelos modelos = get_ensemble() # Evaluar cada modelo resultados = lista() para nombre,modelo en modelos: # Definir el método de evaluación cv = RepeatedStratifiedKFold(n_splits=10, n_repeticiones=3, estado_aleatorio=1) # Evaluar el modelo en el conjunto de datos n_puntuaciones = puntaje_valor_cruzado(modelo, X, y, puntuación=«exactitud, cv=cv, n_jobs=–1) # Informe de rendimiento imprimir(«>%s: %.3f (%.3f) % (nombre, significa(n_puntuaciones), std(n_puntuaciones))) resultados.anexar(n_puntuaciones) # Grafica los resultados para compararlos… pyplot.Boxplot(resultados, etiquetas=[[n para n,_ en modelos], showmeans=Verdadero) pyplot.mostrar() |
La ejecución del ejemplo informa primero de la precisión de la clasificación media y estándar de cada modelo individual, para terminar con el rendimiento del conjunto que combina los modelos.
Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o el procedimiento de evaluación, o las diferencias en la precisión numérica. Considere ejecutar el ejemplo unas cuantas veces y compare el resultado promedio.
En este caso, podemos ver que varios de los miembros individuales tienen un buen desempeño, como «kbins» que alcanza una precisión de alrededor del 83,3 por ciento, y «std«…que alcanza una precisión de alrededor del 83,1 por ciento. También podemos ver que el conjunto logra un mejor rendimiento general en comparación con cualquier miembro contribuyente, con una precisión de alrededor del 83,4 por ciento.
|
>norma: 0.821 (0.041) >std: 0.831 (0.045) >robusto: 0.826 (0.044) >potencia: 0,825 (0,045) >cantidad: 0,817 (0,042) >kbins: 0.833 (0.035) >ensamble: 0.834 (0.040) |
También se crea una figura que muestra gráficos de caja y bigote de la precisión de la clasificación para cada modelo individual, así como el conjunto de transformación de datos.
Podemos ver que la distribución para el conjunto está sesgada, que es lo que podríamos esperar, y que la media (triángulo verde) es ligeramente más alta que la de los miembros individuales del conjunto.
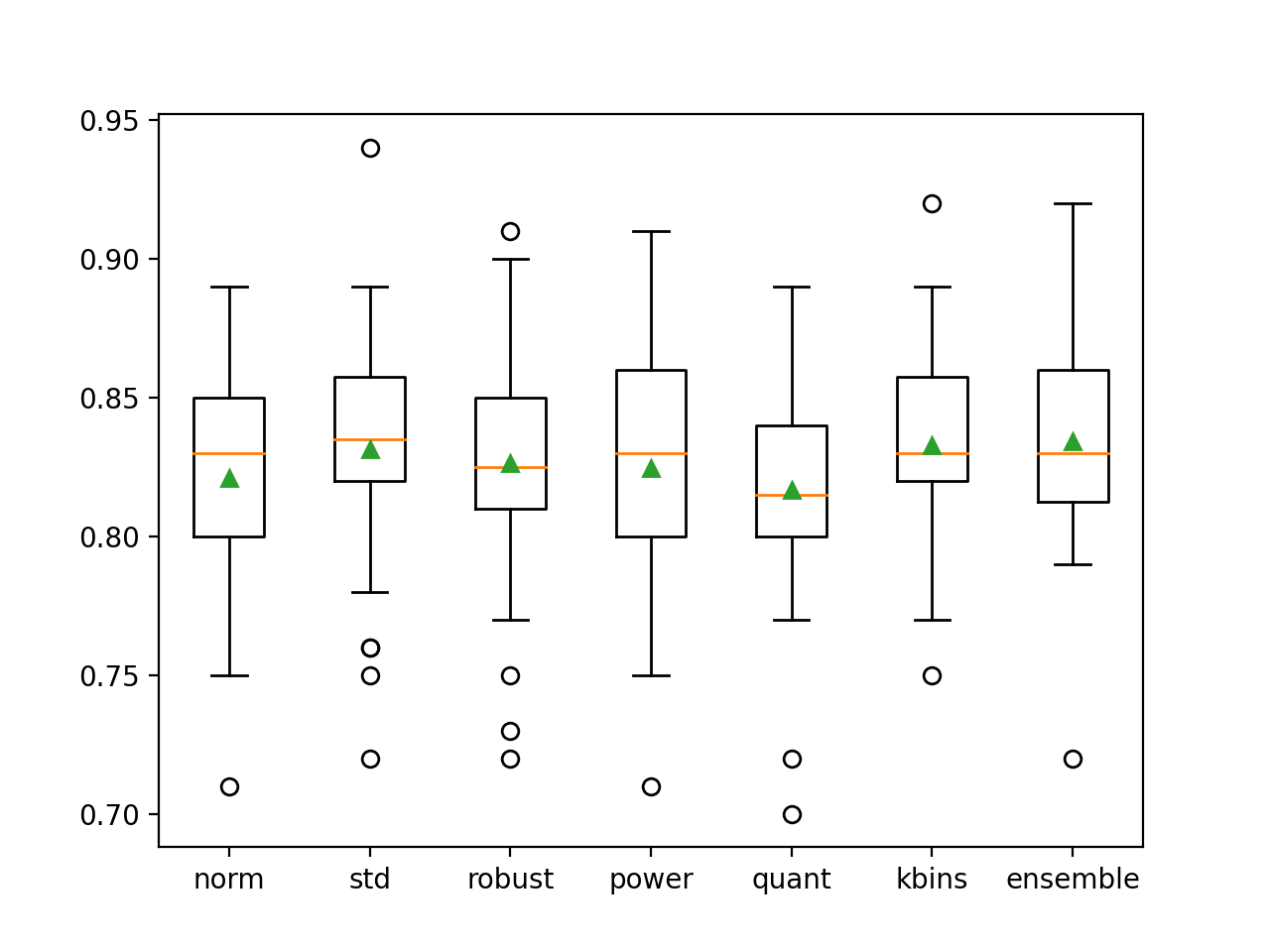
Cuadro y diagrama de bigote de la distribución de la precisión para los modelos individuales y el conjunto de transformación de datos
Ahora que estamos familiarizados con el desarrollo de un conjunto de transformación de datos para la clasificación, veamos cómo hacer lo mismo para la regresión.
Conjunto de transformación de datos para la regresión
En esta sección, exploraremos el desarrollo de un conjunto de transformación de datos para un problema de modelado predictivo de regresión.
Primero, podemos definir un conjunto de datos de regresión binaria sintética como base para explorar este tipo de conjunto.
En el ejemplo que figura a continuación se crea un conjunto de datos con 1.000 ejemplos, cada uno de los cuales contiene 100 características de entrada, de los cuales 10 contienen información para predecir el objetivo.
|
# Conjunto de datos de regresión sintética de sklearn.conjuntos de datos importación hacer_regresión # Definir el conjunto de datos X, y = make_regression(n_muestras=1000, n_funciones=100, n_informativo=10, ruido=0.1, estado_aleatorio=1) # resumir el conjunto de datos imprimir(X.forma, y.forma) |
Ejecutando el ejemplo se crea el conjunto de datos y se confirma que los datos tienen la forma esperada.
A continuación, podemos establecer una línea de base en el desempeño en el conjunto de datos sintéticos mediante el ajuste y la evaluación del modelo base que pretendemos utilizar en el conjunto, en este caso, un DecisionTreeRegressor.
El modelo se evaluará mediante la validación cruzada repetida de tres repeticiones y 10 pliegues. El rendimiento del modelo en el conjunto de datos se informará utilizando el error absoluto medio, o MAE. El scikit-learn invertirá el puntaje (lo hará negativo) para que el marco pueda maximizar el puntaje. Como tal, podemos ignorar el signo de la puntuación.
En el ejemplo que figura a continuación se evalúa el árbol de decisiones en el conjunto de datos de regresión sintética.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# Evaluar el árbol de decisión sobre el conjunto de datos de regresión sintética de numpy importación significa de numpy importación std de sklearn.conjuntos de datos importación make_regression de sklearn.model_selection importación puntaje_valor_cruzado de sklearn.model_selection importación RepetidoKFold de sklearn.árbol importación DecisionTreeRegressor # Definir el conjunto de datos X, y = make_regression(n_muestras=1000, n_funciones=100, n_informativo=10, ruido=0.1, estado_aleatorio=1) # Definir el modelo modelo = DecisionTreeRegressor() # Definir el procedimiento de evaluación cv = RepetidoKFold(n_splits=10, n_repeticiones=3, estado_aleatorio=1) # Evaluar el modelo n_puntuaciones = puntaje_valor_cruzado(modelo, X, y, puntuación=‘neg_mean_absolute_error’, cv=cv, n_jobs=–1) # Informe de rendimiento imprimir(MAE: %.3f (%.3f)’. % (significa(n_puntuaciones), std(n_puntuaciones))) |
Ejecutando el ejemplo se reporta el MAE del árbol de decisión sobre el conjunto de datos de regresión sintética.
Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o el procedimiento de evaluación, o las diferencias en la precisión numérica. Considere ejecutar el ejemplo unas cuantas veces y compare el resultado promedio.
En este caso, podemos ver que el modelo alcanzó un MAE de alrededor de 139.817. Esto proporciona un piso de rendimiento que esperamos que el modelo de conjunto mejore.
A continuación, podemos desarrollar y evaluar el conjunto.
Utilizaremos las mismas transformaciones de datos de la sección anterior. El VotingRegressor se usará para combinar las predicciones, lo que es apropiado para los problemas de regresión.
La función get_ensemble() definida a continuación crea los modelos individuales y el modelo de conjunto y combina todos los modelos como una lista de tuplas para su evaluación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
# Obtener un conjunto de modelos votantes def get_ensemble(): # Definir los modelos de base modelos = lista() # Normalización… norma = Oleoducto([[(‘s’, MinMaxScaler()), (‘m’, DecisionTreeRegressor())]) modelos.anexar((«norma, norma)) # Estandarización std = Oleoducto([[(‘s’, StandardScaler()), (‘m’, DecisionTreeRegressor())]) modelos.anexar((«std, std)) # robusto robusto = Oleoducto([[(‘s’, RobustScaler()), (‘m’, DecisionTreeRegressor())]) modelos.anexar((«robusto, robusto)) # Poder poder = Oleoducto([[(‘s’, Transformador de potencia()), (‘m’, DecisionTreeRegressor())]) modelos.anexar((«poder, poder)) # Cuño quant = Oleoducto([[(‘s’, QuantileTransformer(n_quantiles=100, distribución_de_salida=«normal)), (‘m’, DecisionTreeRegressor())]) modelos.anexar((«quant, quant)) # kbins kbins = Oleoducto([[(‘s’, KBinsDiscretizador(n_bins=20, codificar=«ordinal)), (‘m’, DecisionTreeRegressor())]) modelos.anexar((«kbins, kbins)) # Definir el conjunto de votos conjunto = VotingRegressor(estimadores=modelos) # Devuelve una lista de tuplas, cada una con un nombre y un modelo volver modelos + [[(«conjunto, conjunto)] |
Podemos entonces llamar a esta función y evaluar cada tubería de modelización contribuyente de forma independiente y comparar los resultados con el conjunto de las tuberías.
Nuestra expectativa, como antes, es que el conjunto resulte en un aumento de rendimiento sobre cualquier modelo individual. Si no lo hace, entonces el modelo individual de mayor rendimiento debe ser elegido en su lugar.
Enlazando todo esto, el ejemplo completo para evaluar un conjunto de transformación de datos para un conjunto de datos de regresión se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 |
# Comparación de datos de transformación de conjunto a cada miembro contribuyente para la regresión de numpy importación significa de numpy importación std de sklearn.conjuntos de datos importación make_regression de sklearn.model_selection importación puntaje_valor_cruzado de sklearn.model_selection importación RepetidoKFold de sklearn.preprocesamiento importación MinMaxScaler de sklearn.preprocesamiento importación StandardScaler de sklearn.preprocesamiento importación RobustScaler de sklearn.preprocesamiento importación Transformador de potencia de sklearn.preprocesamiento importación QuantileTransformer de sklearn.preprocesamiento importación KBinsDiscretizador de sklearn.árbol importación DecisionTreeRegressor de sklearn.conjunto importación VotingRegressor de sklearn.tubería importación Oleoducto de matplotlib importación pyplot # Obtener un conjunto de modelos votantes def get_ensemble(): # Definir los modelos de base modelos = lista() # Normalización… norma = Oleoducto([[(‘s’, MinMaxScaler()), (‘m’, DecisionTreeRegressor())]) modelos.anexar((«norma, norma)) # Estandarización std = Oleoducto([[(‘s’, StandardScaler()), (‘m’, DecisionTreeRegressor())]) modelos.anexar((«std, std)) # robusto robusto = Oleoducto([[(‘s’, RobustScaler()), (‘m’, DecisionTreeRegressor())]) modelos.anexar((«robusto, robusto)) # Poder poder = Oleoducto([[(‘s’, Transformador de potencia()), (‘m’, DecisionTreeRegressor())]) modelos.anexar((«poder, poder)) # Cuantilito quant = Oleoducto([[(‘s’, QuantileTransformer(n_quantiles=100, distribución_de_salida=«normal)), (‘m’, DecisionTreeRegressor())]) modelos.anexar((«quant, quant)) # kbins kbins = Oleoducto([[(‘s’, KBinsDiscretizador(n_bins=20, codificar=«ordinal)), (‘m’, DecisionTreeRegressor())]) modelos.anexar((«kbins, kbins)) # Definir el conjunto de votos conjunto = VotingRegressor(estimadores=modelos) # Devuelve una lista de tuplas, cada una con un nombre y un modelo volver modelos + [[(«conjunto, conjunto)] # Generar un conjunto de datos de regresión X, y = make_regression(n_muestras=1000, n_funciones=100, n_informativo=10, ruido=0.1, estado_aleatorio=1) # Consigue modelos modelos = get_ensemble() # Evaluar cada modelo resultados = lista() para nombre,modelo en modelos: # Definir el método de evaluación cv = RepetidoKFold(n_splits=10, n_repeticiones=3, estado_aleatorio=1) # Evaluar el modelo en el conjunto de datos n_puntuaciones = puntaje_valor_cruzado(modelo, X, y, puntuación=‘neg_mean_absolute_error’, cv=cv, n_jobs=–1) # Informe de rendimiento imprimir(«>%s: %.3f (%.3f) % (nombre, significa(n_puntuaciones), std(n_puntuaciones))) resultados.anexar(n_puntuaciones) # Grafica los resultados para compararlos… pyplot.Boxplot(resultados, etiquetas=[[n para n,_ en modelos], showmeans=Verdadero) pyplot.mostrar() |
Ejecutando el ejemplo primero reporta el MAE de cada modelo individual, terminando con el desempeño del conjunto que combina los modelos.
Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o el procedimiento de evaluación, o las diferencias en la precisión numérica. Considere ejecutar el ejemplo unas cuantas veces y compare el resultado promedio.
Podemos ver que cada modelo funciona más o menos igual, con puntuaciones de error del MAE de alrededor de 140, todas más altas que el árbol de decisión utilizado en forma aislada. Curiosamente, el conjunto es el que mejor funciona, superando a todos los miembros individuales y al árbol sin transformaciones, alcanzando un MAE de alrededor de 126.487.
Este resultado sugiere que, aunque cada tubería se desempeña peor que un solo árbol sin transformaciones, cada tubería está cometiendo errores diferentes y que el promedio de los modelos es capaz de apalancar y aprovechar estas diferencias hacia un error menor.
|
>norma: -140.559 (11.783) >std: -140.582 (11.996) >robusto: -140.813 (11.827) >potencia: -141.089 (12.668) >cantidad: -141.109 (11.097) >kbins: -145.134 (11.638) >ensamble: -126.487 (9.999) |
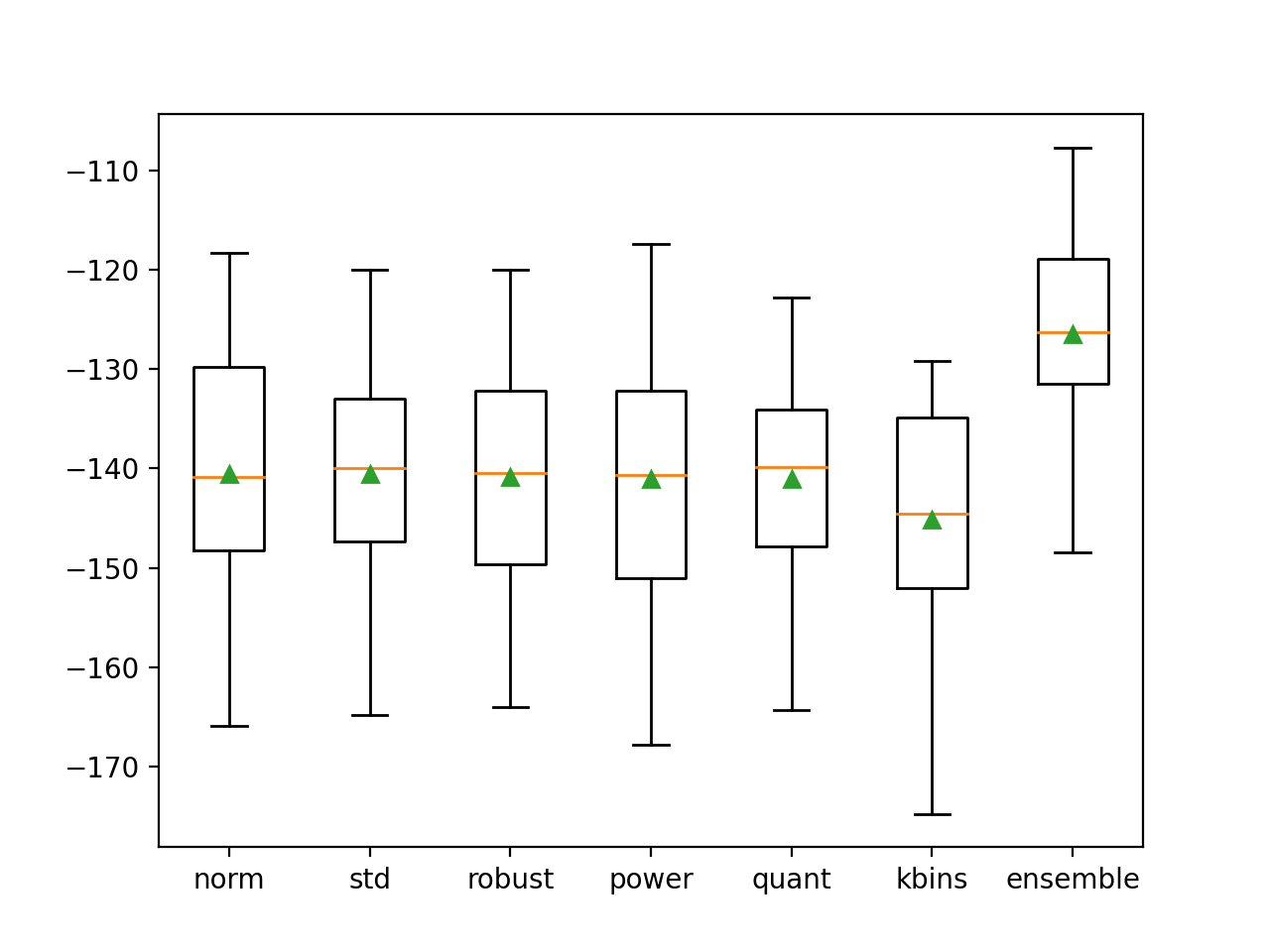
Se crea una figura que compara la distribución de las puntuaciones del MAE para cada tubería y el conjunto.
Como esperábamos, la distribución del conjunto se inclina más en comparación con todos los demás modelos y tiene una tendencia central más alta (más pequeña) (media y mediana indicadas por el triángulo verde y la línea naranja respectivamente).

Cuadro y diagrama de bigote de las distribuciones del MAE para los modelos individuales y el conjunto de transformación de datos
Más lecturas
Esta sección proporciona más recursos sobre el tema si desea profundizar en él.
Tutoriales
Libros
APIs
Resumen
En este tutorial, descubriste cómo desarrollar un conjunto de transformación de datos.
Específicamente, aprendiste:
- Las transformaciones de datos pueden utilizarse como base para un conjunto de tipo «bagging» en el que el mismo modelo se entrena en diferentes vistas de un conjunto de datos de entrenamiento.
- Cómo desarrollar un conjunto de transformación de datos para la clasificación y confirmar que el conjunto funciona mejor que cualquier miembro contribuyente.
- Cómo desarrollar y evaluar un conjunto de transformación de datos para el modelado predictivo de regresión.
¿Tiene alguna pregunta?
Haga sus preguntas en los comentarios de abajo y haré lo posible por responder.
