XGBoost es una implementación eficiente de la potenciación de gradientes para los problemas de clasificación y regresión.
Es rápido y eficiente, y funciona bien, si no es el mejor, en una amplia gama de tareas de modelado predictivo y es el favorito entre los ganadores de concursos de ciencias de la información, como los de Kaggle.
XGBoost también puede utilizarse para la previsión de series temporales, aunque requiere que el conjunto de datos de series temporales se transforme primero en un problema de aprendizaje supervisado. También requiere el uso de una técnica especializada para evaluar el modelo llamada validación de avance, ya que la evaluación del modelo mediante la validación cruzada de pliegues k daría lugar a resultados sesgados de manera optimista.
En este tutorial, descubrirás cómo desarrollar un modelo XGBoost para la previsión de series temporales.
Después de completar este tutorial, lo sabrás:
- XGBoost es una implementación del algoritmo de conjunto de potenciación de gradientes para la clasificación y la regresión.
- Los conjuntos de datos de series temporales pueden transformarse en aprendizaje supervisado mediante una representación de ventana deslizante.
- Cómo encajar, evaluar y hacer predicciones con un modelo XGBoost para la previsión de series temporales.
Empecemos.

Cómo utilizar XGBoost para la previsión de series temporales
Foto de Ghopotam, algunos derechos reservados.
Resumen del Tutorial
Este tutorial está dividido en tres partes; son:
- Conjunto XGBoost
- Preparación de datos de series de tiempo
- XGBoost para la previsión de series temporales
Conjunto XGBoost
XGBoost es la abreviatura de Extreme Gradient Boosting y es una implementación eficiente del algoritmo de aprendizaje de la máquina de impulso de gradiente estocástico.
El algoritmo de aumento de gradiente estocástico, también llamado máquinas de aumento de gradiente o aumento de árbol, es una poderosa técnica de aprendizaje de máquinas que funciona bien o incluso mejor en una amplia gama de problemas de aprendizaje de máquinas desafiantes.
Se ha demostrado que la potenciación de los árboles da resultados de vanguardia en muchos puntos de referencia de clasificación estándar.
– XGBoost: Un sistema de potenciación de árboles escalable, 2016.
Es un conjunto de árboles de decisión algorítmicos donde los nuevos árboles arreglan los errores de los árboles que ya forman parte del modelo. Los árboles se añaden hasta que no se pueden hacer más mejoras en el modelo.
XGBoost proporciona una implementación altamente eficiente del algoritmo de aumento del gradiente estocástico y acceso a un conjunto de hiperparámetros de modelos diseñados para proporcionar control sobre el proceso de entrenamiento de los modelos.
El factor más importante del éxito del XGBoost es su escalabilidad en todos los escenarios. El sistema funciona más de diez veces más rápido que las soluciones populares existentes en una sola máquina y escala a miles de millones de ejemplos en configuraciones distribuidas o de memoria limitada.
– XGBoost: Un sistema de potenciación de árboles escalable, 2016.
XGBoost está diseñado para la clasificación y la regresión en conjuntos de datos tabulares, aunque puede utilizarse para la previsión de series temporales.
Para más información sobre el aumento del gradiente y la implementación de XGBoost, ver el tutorial:
Primero, la biblioteca XGBoost debe ser instalada.
Puedes instalarlo usando pip, como sigue:
Una vez instalado, puede confirmar que se instaló con éxito y que está utilizando una versión moderna ejecutando el siguiente código:
|
# xgboost importación xgboost imprimir(«xgboost», xgboost.La versión…) |
Al ejecutar el código, debería ver el siguiente número de versión o superior.
Aunque la biblioteca XGBoost tiene su propio API en Python, podemos utilizar los modelos de XGBoost con el API scikit-learn a través de la clase envolvente XGBRegressor.
Una instancia del modelo puede ser instanciada y utilizada como cualquier otra clase de aprendizaje científico para la evaluación del modelo. Por ejemplo:
|
... # Definir el modelo modelo = XGBRegressor() |
Ahora que estamos familiarizados con el XGBoost, veamos cómo podemos preparar un conjunto de datos de series temporales para el aprendizaje supervisado.
Preparación de datos de series de tiempo
Los datos de las series de tiempo pueden formularse como aprendizaje supervisado.
Dada una secuencia de números para un conjunto de datos de series temporales, podemos reestructurar los datos para que parezcan un problema de aprendizaje supervisado. Podemos hacer esto utilizando los pasos de tiempo anteriores como variables de entrada y utilizar el siguiente paso de tiempo como la variable de salida.
Concretemos esto con un ejemplo. Imaginemos que tenemos una serie temporal como la siguiente:
|
tiempo, medir 1, 100 2, 110 3, 108 4, 115 5, 120 |
Podemos reestructurar este conjunto de datos de series temporales como un problema de aprendizaje supervisado utilizando el valor en el paso de tiempo anterior para predecir el valor en el siguiente paso de tiempo.
Reorganizando el conjunto de datos de las series de tiempo de esta manera, los datos se verían de la siguiente manera:
|
X, y ?, 100 100, 110 110, 108 108, 115 115, 120 120, ? |
Obsérvese que la columna de tiempo se ha eliminado y que algunas filas de datos son inutilizables para entrenar un modelo, como la primera y la última.
Esta representación se llama ventana corrediza, ya que la ventana de entradas y salidas esperadas se desplaza hacia adelante a través del tiempo para crear nuevas «muestras» para un modelo de aprendizaje supervisado.
Para más información sobre el enfoque de la ventana corrediza para la preparación de datos de previsión de series temporales, véase el tutorial:
Podemos usar la función shift() en Pandas para crear automáticamente nuevos encuadres de problemas de series temporales dada la longitud deseada de las secuencias de entrada y salida.
Esta sería una herramienta útil ya que nos permitiría explorar diferentes encuadres de un problema de series temporales con algoritmos de aprendizaje de máquinas para ver cuál podría resultar en modelos de mejor rendimiento.
La función que se indica a continuación tomará una serie temporal como una serie temporal de la matriz NumPy con una o más columnas y la transformará en un problema de aprendizaje supervisado con el número especificado de entradas y salidas.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# Transformar un conjunto de datos de series de tiempo en un conjunto de datos de aprendizaje supervisado # def serie_a_supervisada(datos, n_in=1, n_out=1, dropnan=Verdadero): n_vars = 1 si escriba(datos) es lista más datos.forma[[1] df = DataFrame(datos) cols = lista() # Secuencia de entrada (t-n, … t-1) para i en rango(n_in, 0, –1): cols.anexar(df.turno(i)) # Secuencia de pronóstico (t, t+1, … t+n) para i en rango(0, n_out): cols.anexar(df.turno(–i)) # Poner todo junto agg = concat(cols, eje=1) # Filas de caída con valores de NaN si dropnan: agg.dropna(en el lugar=Verdadero) volver agg.valores |
Podemos usar esta función para preparar un conjunto de datos de series temporales para XGBoost.
Para más información sobre el desarrollo paso a paso de esta función, véase el tutorial:
Una vez preparado el conjunto de datos, debemos ser cuidadosos en la forma en que se utiliza para ajustar y evaluar un modelo.
Por ejemplo, no sería válido ajustar el modelo con datos del futuro y hacer que prediga el pasado. El modelo debe entrenarse en el pasado y predecir el futuro.
Esto significa que los métodos que aleatorizan el conjunto de datos durante la evaluación, como la validación cruzada del pliegue k, no pueden utilizarse. En su lugar, debemos utilizar una técnica llamada validación a pie de página.
En la validación del avance, el conjunto de datos se divide primero en trenes y conjuntos de pruebas seleccionando un punto de corte, por ejemplo, todos los datos excepto los últimos 12 meses se utilizan para el entrenamiento y los últimos 12 meses para las pruebas.
Si estamos interesados en hacer un pronóstico de un paso, por ejemplo un mes, entonces podemos evaluar el modelo entrenando en el conjunto de datos de entrenamiento y prediciendo el primer paso en el conjunto de datos de la prueba. Podemos entonces añadir la observación real del conjunto de pruebas al conjunto de datos de entrenamiento, reajustar el modelo, y luego hacer que el modelo prediga el segundo paso en el conjunto de datos de la prueba.
La repetición de este proceso para todo el conjunto de datos de la prueba dará una predicción de un paso para todo el conjunto de datos de la prueba a partir de la cual se puede calcular una medida de error para evaluar la habilidad del modelo.
Para más información sobre la validación de la marcha adelante, vea el tutorial:
La función que se indica a continuación realiza la validación de la marcha adelante.
Se necesita toda la versión de aprendizaje supervisado del conjunto de datos de la serie de tiempo y el número de filas para usar como argumento el conjunto de pruebas.
Luego pasa por el conjunto de pruebas, llamando al xgboost_forecast() para hacer un pronóstico de un solo paso. Se calcula una medida de error y se devuelven los detalles para su análisis.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
# Validación de los datos univariados def validación_de_caminata(datos, n_test): predicciones = lista() # Split dataset tren, prueba = prueba_de_trenes_split(datos, n_test) # Historia de la semilla con el conjunto de datos de entrenamiento historia = [[x para x en tren] # paso a paso en cada paso de tiempo en el conjunto de la prueba para i en rango(len(prueba)): # Dividir la fila de prueba en columnas de entrada y salida testX, testy = prueba[[i, :–1], prueba[[i, –1] # Encajar el modelo en la historia y hacer una predicción yhat = xgboost_forecast(historia, testX) # Almacenar la predicción en la lista de predicciones predicciones.anexar(yhat) # Agregar la observación real a la historia para el próximo ciclo historia.anexar(prueba[[i]) # Resumir el progreso… imprimir(‘>esperado=%.1f, pronosticado=%.1f’ % (testy, yhat)) # Estimar el error de predicción error = error_absoluto_medio(prueba[[:, 1], predicciones) volver error, prueba[[:, 1], predicciones |
El train_test_split() se llama a la función de dividir el conjunto de datos en trenes y conjuntos de pruebas.
Podemos definir esta función a continuación.
|
# Dividir un conjunto de datos univariados en conjuntos de tren/prueba def prueba_de_trenes_split(datos, n_test): volver datos[[:–n_test, :], datos[[–n_test:, :] |
Podemos usar el XGBRegressor para hacer un pronóstico de un paso.
El xgboost_forecast() La función que se indica a continuación implementa esto, tomando el conjunto de datos de entrenamiento y la fila de entrada de prueba como entrada, ajustando un modelo y haciendo una predicción de un paso.
|
# Encajar un modelo xgboost y hacer una predicción de un paso def xgboost_forecast(tren, testX): # Transformar la lista en una matriz tren = asarray(tren) # Dividido en columnas de entrada y salida trainX, trainy = tren[[:, :–1], tren[[:, –1] # Modelo de ajuste modelo = XGBRegressor(objetivo=«reg:squarederror, n_estimadores=1000) modelo.encajar(trainX, trainy) # hacer una predicción de un paso yhat = modelo.predecir([[testX]) volver yhat[[0] |
Ahora que sabemos cómo preparar datos de series temporales para predecir y evaluar un modelo XGBoost, a continuación podemos ver cómo usar XGBoost en un conjunto de datos reales.
XGBoost para la previsión de series temporales
En esta sección, exploraremos cómo utilizar el XGBoost para la previsión de series temporales.
Utilizaremos un conjunto de datos estándar de series temporales univariadas con la intención de utilizar el modelo para hacer un pronóstico de un solo paso.
Puede utilizar el código de esta sección como punto de partida de su propio proyecto y adaptarlo fácilmente para entradas multivariadas, previsiones multivariadas y previsiones de varios pasos.
Usaremos el conjunto de datos de los nacimientos femeninos diarios, es decir, los nacimientos mensuales a lo largo de tres años.
Puede descargar el conjunto de datos desde aquí, colóquelo en su directorio de trabajo actual con el nombre de archivo «daily-total-female-births.csv“.
Las primeras líneas del conjunto de datos se ven como sigue:
|
«Fecha», «Nacimientos» «1959-01-01»,35 «1959-01-02»,32 «1959-01-03»,30 «1959-01-04»,31 «1959-01-05»,44 … |
Primero, carguemos y tracemos el conjunto de datos.
El ejemplo completo figura a continuación.
|
# Cargar y trazar el conjunto de datos de las series de tiempo de pandas importación read_csv de matplotlib importación pyplot # Cargar conjunto de datos serie = read_csv(‘daily-total-female-births.csv’, encabezado=0, index_col=0) valores = serie.valores # conjunto de datos de la trama pyplot.parcela(valores) pyplot.mostrar() |
Ejecutando el ejemplo se crea un gráfico de líneas del conjunto de datos.
Podemos ver que no hay una tendencia obvia o estacionalidad.
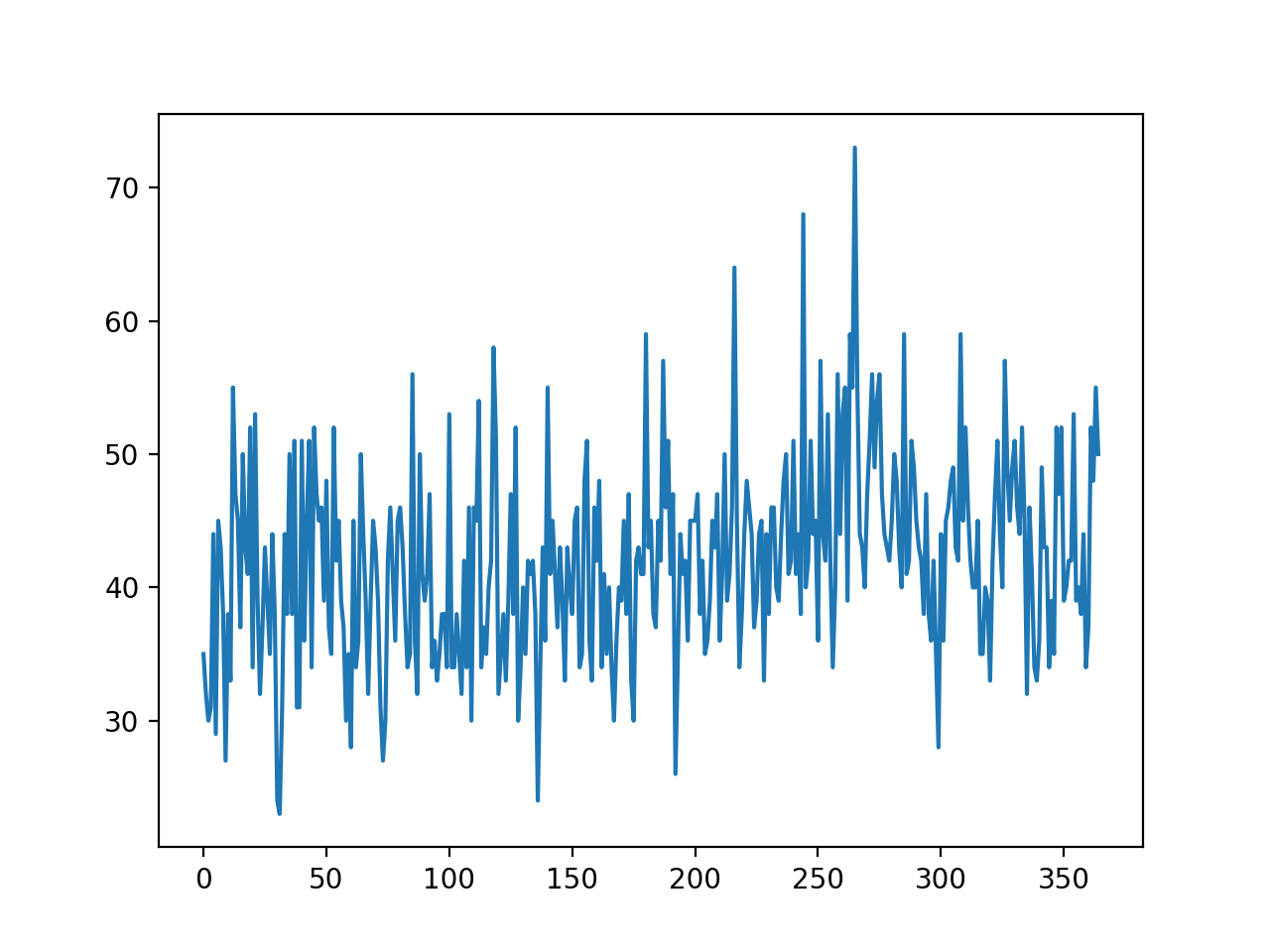
Gráfica de línea de nacimientos mensuales Conjunto de datos de series temporales
Un modelo de persistencia puede lograr un MAE de alrededor de 6,7 nacimientos al predecir los últimos 12 meses. Esto proporciona una línea de base en el rendimiento por encima de la cual un modelo puede considerarse hábil.
A continuación, podemos evaluar el modelo XGBoost en el conjunto de datos al hacer previsiones de un solo paso para los últimos 12 meses de datos.
Usaremos sólo los tres pasos de tiempo anteriores como entrada al modelo y a los hiperparámetros del modelo por defecto, excepto que cambiaremos la pérdida por ‘reg:squarederror(para evitar un mensaje de advertencia) y utilizar un conjunto de 1000 árboles (para evitar el subaprendizaje).
El ejemplo completo figura a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 |
# Previsión de nacimientos mensuales con xgboost de numpy importación asarray de pandas importación read_csv de pandas importación DataFrame de pandas importación concat de sklearn.métrica importación error_absoluto_medio de xgboost importación XGBRegressor de matplotlib importación pyplot # Transformar un conjunto de datos de series de tiempo en un conjunto de datos de aprendizaje supervisado def serie_a_supervisada(datos, n_in=1, n_out=1, dropnan=Verdadero): n_vars = 1 si escriba(datos) es lista más datos.forma[[1] df = DataFrame(datos) cols = lista() # Secuencia de entrada (t-n, … t-1) para i en rango(n_in, 0, –1): cols.anexar(df.turno(i)) # Secuencia de pronóstico (t, t+1, … t+n) para i en rango(0, n_out): cols.anexar(df.turno(–i)) # Poner todo junto agg = concat(cols, eje=1) # Filas de caída con valores de NaN si dropnan: agg.dropna(en el lugar=Verdadero) volver agg.valores # Dividir un conjunto de datos univariados en conjuntos de tren/prueba def prueba_de_trenes_split(datos, n_test): volver datos[[:–n_test, :], datos[[–n_test:, :] # Encajar un modelo xgboost y hacer una predicción de un paso def xgboost_forecast(tren, testX): # Transformar la lista en una matriz tren = asarray(tren) # Dividido en columnas de entrada y salida trainX, trainy = tren[[:, :–1], tren[[:, –1] # Modelo de ajuste modelo = XGBRegressor(objetivo=«reg:squarederror, n_estimadores=1000) modelo.encajar(trainX, trainy) # hacer una predicción de un paso yhat = modelo.predecir(asarray([[testX])) volver yhat[[0] # Validación de los datos univariados def validación_de_caminata(datos, n_test): predicciones = lista() # Split dataset tren, prueba = prueba_de_trenes_split(datos, n_test) # Historia de la semilla con el conjunto de datos de entrenamiento historia = [[x para x en tren] # paso a paso en cada paso de tiempo en el conjunto de la prueba para i en rango(len(prueba)): # Dividir la fila de prueba en columnas de entrada y salida testX, testy = prueba[[i, :–1], prueba[[i, –1] # Encajar el modelo en la historia y hacer una predicción yhat = xgboost_forecast(historia, testX) # Almacenar la predicción en la lista de predicciones predicciones.anexar(yhat) # Agregar la observación real a la historia para el próximo ciclo historia.anexar(prueba[[i]) # Resumir el progreso… imprimir(‘>esperado=%.1f, pronosticado=%.1f’ % (testy, yhat)) # Estimar el error de predicción error = error_absoluto_medio(prueba[[:, 1], predicciones) volver error, prueba[[:, 1], predicciones # Cargar el conjunto de datos serie = read_csv(‘daily-total-female-births.csv’, encabezado=0, index_col=0) valores = serie.valores # Transformar los datos de las series temporales en aprendizaje supervisado datos = serie_a_supervisada(valores, n_in=3) # Evaluar mae, y, yhat = validación_de_caminata(datos, 12) imprimir(MAE: %.3f % mae) # trama esperada vs. preducida pyplot.parcela(y, etiqueta=«Esperado) pyplot.parcela(yhat, etiqueta=«Predicho) pyplot.leyenda() pyplot.mostrar() |
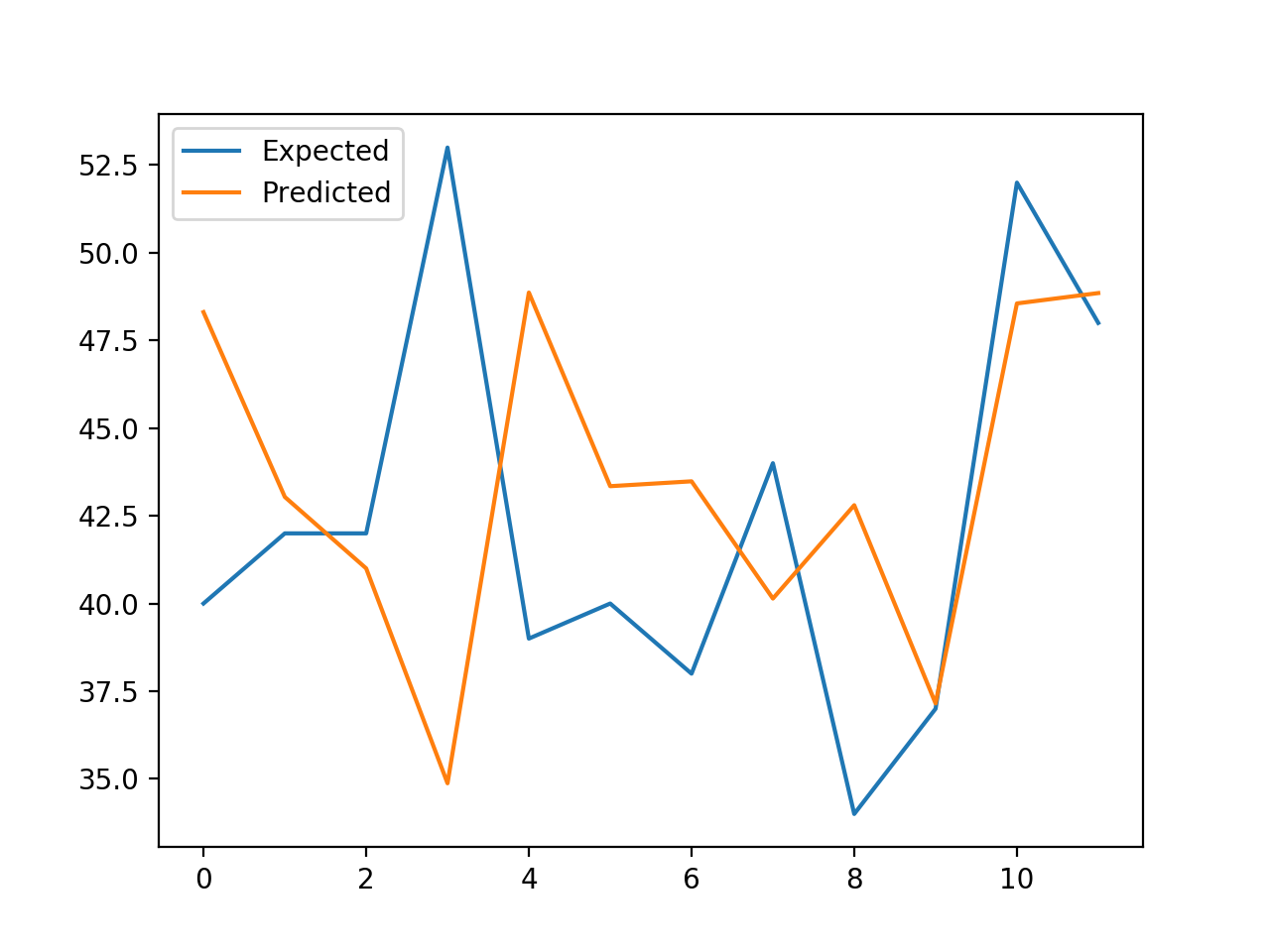
La ejecución del ejemplo reporta los valores esperados y pronosticados para cada paso del conjunto de pruebas, luego el MAE para todos los valores pronosticados.
Podemos ver que el modelo funciona mejor que un modelo de persistencia, logrando un MAE de unos 5,3 nacimientos, en comparación con 6,7 nacimientos.
¿Puedes hacerlo mejor?
Puedes probar diferentes hiperparámetros XGBoost y números de pasos de tiempo como entrada para ver si puedes conseguir un mejor rendimiento. Comparte tus resultados en los siguientes comentarios.
|
>esperado=42.0, pronosticado=48.3 >esperado=53.0, pronosticado=43.0 >esperado=39.0, pronosticado=41.0 >previsto=40,0, pronosticado=34,9 >esperado=38.0, pronosticado=48.9 >esperado=44,0, pronosticado=43,3 >esperado=34.0, pronosticado=43.5 >esperado=37.0, pronosticado=40.1 >esperado=52.0, pronosticado=42.8 >esperado=48,0, pronosticado=37,2 >esperado=55.0, pronosticado=48.6 >expected=50.0, predicho=48.9 MAE: 5.356 |
Se crea una gráfica lineal que compara la serie de valores esperados y los valores predichos para los últimos 12 meses del conjunto de datos.
Esto da una interpretación geométrica de lo bien que el modelo funcionó en el conjunto de pruebas.

Gráfica de líneas de nacimientos esperados vs. previstos usando XGBoost
Una vez elegida una configuración final del modelo XGBoost, se puede finalizar el modelo y utilizarlo para hacer una predicción sobre nuevos datos.
Esto se llama pronóstico fuera de muestra…por ejemplo, predecir más allá del conjunto de datos de entrenamiento. Esto es idéntico a hacer una predicción durante la evaluación del modelo: ya que siempre queremos evaluar un modelo usando el mismo procedimiento que esperamos usar cuando el modelo se usa para hacer una predicción sobre nuevos datos.
El ejemplo que se presenta a continuación demuestra el ajuste de un modelo final de XGBoost en todos los datos disponibles y la realización de una predicción de un paso más allá del final del conjunto de datos.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
# Finalizar el modelo y hacer una predicción de los nacimientos mensuales con xgboost de numpy importación asarray de pandas importación read_csv de pandas importación DataFrame de pandas importación concat de xgboost importación XGBRegressor # Transformar un conjunto de datos de series de tiempo en un conjunto de datos de aprendizaje supervisado def serie_a_supervisada(datos, n_in=1, n_out=1, dropnan=Verdadero): n_vars = 1 si escriba(datos) es lista más datos.forma[[1] df = DataFrame(datos) cols = lista() # Secuencia de entrada (t-n, … t-1) para i en rango(n_in, 0, –1): cols.anexar(df.turno(i)) # Secuencia de pronóstico (t, t+1, … t+n) para i en rango(0, n_out): cols.anexar(df.turno(–i)) # Poner todo junto agg = concat(cols, eje=1) # Filas de caída con valores de NaN si dropnan: agg.dropna(en el lugar=Verdadero) volver agg.valores # Cargar el conjunto de datos serie = read_csv(‘daily-total-female-births.csv’, encabezado=0, index_col=0) valores = serie.valores # Transformar los datos de las series temporales en aprendizaje supervisado tren = serie_a_supervisada(valores, n_in=3) # Dividido en columnas de entrada y salida trainX, trainy = tren[[:, :–1], tren[[:, –1] # Modelo de ajuste modelo = XGBRegressor(objetivo=«reg:squarederror, n_estimadores=1000) modelo.encajar(trainX, trainy) # Construir una entrada para una nueva preducción fila = valores[[–3:].aplanar() # hacer una predicción de un paso yhat = modelo.predecir(asarray([[fila])) imprimir(«Entrada: %s, Predicho: %.3f % (fila, yhat[[0])) |
Ejecutando el ejemplo se ajusta un modelo XGBoost en todos los datos disponibles.
Se prepara una nueva fila de entradas utilizando los últimos tres meses de datos conocidos y se predice el siguiente mes después del final del conjunto de datos.
|
Entrada: [48 55 50]Predicho: 46.736 |
