Conjunto subespacial aleatorio es un algoritmo de aprendizaje automático que combina las predicciones de múltiples árboles de decisión entrenados en diferentes subconjuntos de columnas del conjunto de datos de entrenamiento.
Variar al azar las columnas utilizadas para entrenar a cada miembro contribuyente del conjunto tiene el efecto de introducir diversidad en el conjunto y, a su vez, puede elevar la actuación por encima del uso de un único árbol de decisiones.
Está relacionado con otros conjuntos de árboles de decisión como la agregación de bootstrap (embolsado) que crea árboles utilizando diferentes muestras de filas del conjunto de datos de formación, y el bosque aleatorio que combina ideas de embolsado y el conjunto subespacial aleatorio.
Aunque a menudo se utilizan árboles de decisión, el método subespacial aleatorio general puede utilizarse con cualquier modelo de aprendizaje por máquina cuyo rendimiento varíe significativamente con la elección de las características de entrada.
En este tutorial, descubrirá cómo desarrollar conjuntos subespaciales aleatorios para la clasificación y la regresión.
Después de completar este tutorial, lo sabrás:
- Se crean conjuntos subespaciales aleatorios a partir de árboles de decisión que se ajustan a diferentes muestras de características (columnas) en el conjunto de datos de entrenamiento.
- Cómo usar el conjunto subespacial aleatorio para la clasificación y regresión con scikit-learn.
- Cómo explorar el efecto de los hiperparámetros de los modelos subespaciales aleatorios en el rendimiento de los modelos.
Empecemos.

Cómo desarrollar un conjunto subespacial aleatorio con Python
Foto de Marsel Minga, algunos derechos reservados.
Resumen del Tutorial
Este tutorial está dividido en tres partes; son:
- Conjunto subespacial aleatorio
- Ensamble subespacial aleatorio a través de embolsado
- Conjunto subespacial aleatorio para la clasificación
- Conjunto subespacial aleatorio para la regresión
- Conjunto subespacial aleatorio de hiperparámetros
- Explorar el número de árboles
- Explorar el número de características
- Explorar el algoritmo alternativo
Conjunto subespacial aleatorio
Un problema de modelado predictivo consiste en una o más variables de entrada y una variable objetivo.
Una variable es una columna en los datos y también se suele denominar característica. Podemos considerar que todos los rasgos de entrada juntos definen un espacio vectorial de n dimensiones, donde n es el número de rasgos de entrada y cada ejemplo (fila de datos de entrada) es un punto en el espacio del rasgo.
Se trata de una conceptualización común en el aprendizaje de las máquinas y, a medida que los espacios de las características de entrada se hacen más grandes, aumenta la distancia entre los puntos del espacio, lo que se conoce generalmente como la maldición de la dimensionalidad.
Por lo tanto, un subconjunto de características de entrada puede considerarse como un subconjunto del espacio de características de entrada, o un subespacio.
La selección de características es una forma de definir un subespacio del espacio de características de entrada. Por ejemplo, la selección de rasgos se refiere a un intento de reducir el número de dimensiones del espacio del rasgo de entrada seleccionando un subconjunto de rasgos para mantener o un subconjunto de rasgos para eliminar, a menudo basado en su relación con la variable objetivo.
Alternativamente, podemos seleccionar subconjuntos aleatorios de características de entrada para definir subespacios aleatorios. Esto puede utilizarse como base para un algoritmo de aprendizaje en conjunto, en el que se puede ajustar un modelo en cada subespacio aleatorio de características. Esto se denomina conjunto de subespacios aleatorios o método subespacial aleatorio.
Los datos de entrenamiento suelen describirse mediante un conjunto de características. Diferentes subconjuntos de características, o llamados subespacios, proporcionan diferentes puntos de vista sobre los datos. Por lo tanto, los alumnos individuales capacitados desde diferentes subespacios suelen ser diversos.
– Página 116, Métodos de ensamblaje, 2012.
Fue propuesto por Tin Kam Ho en el documento de 1998 titulado «The Random Subspace Method For Constructing Decision Forests» (El método del subespacio aleatorio para la construcción de bosques de decisión), en el que se ajusta un árbol de decisión en cada subespacio aleatorio.
En términos más generales, se trata de una técnica de diversidad para el aprendizaje en conjunto que pertenece a una clase de métodos que cambian el conjunto de datos de capacitación para cada modelo en el intento de reducir la correlación entre las predicciones de los modelos en el conjunto.
El procedimiento es tan simple como seleccionar un subconjunto aleatorio de características de entrada (columnas) para cada modelo en el conjunto y ajustar el modelo en el modelo en todo el conjunto de datos de entrenamiento. Se puede aumentar con cambios adicionales, como el uso de un bootstrap o una muestra aleatoria de las filas en el conjunto de datos de entrenamiento.
El clasificador consiste en múltiples árboles construidos sistemáticamente mediante la selección seudoaleatoria de subconjuntos de componentes del vector del rasgo, es decir, árboles construidos en subespacios elegidos al azar.
– El método subespacial aleatorio para la construcción de bosques de decisión, 1998.
Como tal, el conjunto subespacial aleatorio está relacionado con la agregación (empaquetamiento) de bootstrap que introduce la diversidad al entrenar cada modelo, a menudo un árbol de decisiones, en una muestra aleatoria diferente del conjunto de datos de entrenamiento, con reemplazo (por ejemplo, el método de muestreo de bootstrap). El conjunto aleatorio de bosques también puede considerarse un híbrido de los métodos de embolsado y de conjunto aleatorio de subconjuntos.
Los algoritmos que utilizan diferentes subconjuntos de características se denominan comúnmente métodos subespaciales aleatorios…
– Página 21, Ensemble Machine Learning, 2012.
El método subespacial aleatorio puede utilizarse con cualquier algoritmo de aprendizaje de máquina, aunque es muy adecuado para modelos que son sensibles a grandes cambios en las características de entrada, como los árboles de decisión y los vecinos más cercanos.
Es apropiado para los conjuntos de datos que tienen un gran número de características de entrada, ya que puede dar lugar a un buen rendimiento con una buena eficiencia. Si el conjunto de datos contiene muchas características de entrada irrelevantes, puede ser mejor utilizar la selección de características como técnica de preparación de datos, ya que la prevalencia de características irrelevantes en los subespacios puede perjudicar el rendimiento del conjunto.
Para datos con muchas características redundantes, entrenar a un alumno en un subespacio no sólo será efectivo sino también eficiente.
– Página 116, Métodos de ensamblaje, 2012.
Ahora que estamos familiarizados con el conjunto subespacial aleatorio, exploremos cómo podemos implementar el enfoque.
Ensamble subespacial aleatorio a través de embolsado
Podemos implementar el conjunto subespacial aleatorio usando el embolsamiento en el scikit-learn.
El embolsado se realiza a través de las clases BaggingRegressor y BaggingClassifier.
Podemos configurar el embolsado para que sea un conjunto subespacial aleatorio, estableciendo el «bootstrap«argumento para»Falso» para desactivar el muestreo de las filas del conjunto de datos de entrenamiento y establecer el número máximo de características a un valor dado a través del «max_features«argumento».
El modelo por defecto para el embolsado es un árbol de decisión, pero puede ser cambiado a cualquier modelo que queramos.
Podemos demostrar usando el embolsado para implementar un conjunto subespacial aleatorio con árboles de decisión para la clasificación y la regresión.
Conjunto subespacial aleatorio para la clasificación
En esta sección, veremos el desarrollo de un conjunto subespacial aleatorio utilizando el embolsado para un problema de clasificación.
Primero, podemos usar la función make_classification() para crear un problema de clasificación binaria sintética con 1.000 ejemplos y 20 características de entrada.
El ejemplo completo figura a continuación.
|
# Conjunto de datos de clasificación de pruebas de sklearn.conjuntos de datos importación hacer_clasificación # Definir el conjunto de datos X, y = make_classification(n_muestras=1000, n_funciones=20, n_informativo=15, n_redundante=5, estado_aleatorio=5) # resumir el conjunto de datos imprimir(X.forma, y.forma) |
Ejecutando el ejemplo se crea el conjunto de datos y se resume la forma de los componentes de entrada y salida.
A continuación, podemos configurar un modelo de embolsado para ser un conjunto subespacial aleatorio para árboles de decisión en este conjunto de datos.
Cada modelo se ajustará en un subespacio aleatorio de 10 características de entrada, elegidas arbitrariamente.
|
... # Definir el modelo de conjunto subespacial aleatorio modelo = BaggingClassifier(bootstrap=Falso, max_features=10) |
Evaluaremos el modelo utilizando la validación cruzada estratificada k-pliegue, con tres repeticiones y 10 pliegues. Informaremos la media y la desviación estándar de la precisión del modelo en todas las repeticiones y pliegues.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# Evaluar el conjunto subespacial aleatorio a través de la bolsa para la clasificación de numpy importación significa de numpy importación std de sklearn.conjuntos de datos importación make_classification de sklearn.model_selection importación puntaje_valor_cruzado de sklearn.model_selection importación RepeatedStratifiedKFold de sklearn.conjunto importación BaggingClassifier # Definir el conjunto de datos X, y = make_classification(n_muestras=1000, n_funciones=20, n_informativo=15, n_redundante=5, estado_aleatorio=5) # Definir el modelo de conjunto subespacial aleatorio modelo = BaggingClassifier(bootstrap=Falso, max_features=10) # Definir el método de evaluación cv = RepeatedStratifiedKFold(n_splits=10, n_repeticiones=3, estado_aleatorio=1) # Evaluar el modelo en el conjunto de datos n_puntuaciones = puntaje_valor_cruzado(modelo, X, y, puntuación=«exactitud, cv=cv, n_jobs=–1) # Informe de rendimiento imprimir(«Precisión media: %.3f (%.3f) % (significa(n_puntuaciones), std(n_puntuaciones))) |
La ejecución del ejemplo informa de la precisión de la media y la desviación estándar del modelo.
Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o el procedimiento de evaluación, o las diferencias en la precisión numérica. Considere ejecutar el ejemplo unas cuantas veces y compare el resultado promedio.
En este caso, podemos ver que el conjunto subespacial aleatorio con hiperparámetros predeterminados logra una precisión de clasificación de alrededor del 85,4 por ciento en este conjunto de datos de prueba.
|
Precisión media: 0,854 (0,039) |
También podemos usar el modelo de conjunto subespacial aleatorio como modelo final y hacer predicciones para la clasificación.
Primero, el conjunto se ajusta a todos los datos disponibles, luego el predecir() se puede llamar a la función para hacer predicciones sobre nuevos datos.
El siguiente ejemplo lo demuestra en nuestro conjunto de datos de clasificación binaria.
|
# Hacer predicciones usando un conjunto subespacial aleatorio a través de la bolsa para la clasificación de sklearn.conjuntos de datos importación make_classification de sklearn.conjunto importación BaggingClassifier # Definir el conjunto de datos X, y = make_classification(n_muestras=1000, n_funciones=20, n_informativo=15, n_redundante=5, estado_aleatorio=5) # Definir el modelo modelo = BaggingClassifier(bootstrap=Falso, max_features=10) # Encajar el modelo en todo el conjunto de datos modelo.encajar(X, y) # hacer una sola predicción fila = [[[[–4.7705504,–1.88685058,–0.96057964,2.53850317,–6.5843005,3.45711663,–7.46225013,2.01338213,–0.45086384,–1.89314931,–2.90675203,–0.21214568,–0.9623956,3.93862591,0.06276375,0.33964269,4.0835676,1.31423977,–2.17983117,3.1047287]] yhat = modelo.predecir(fila) imprimir(Clase prevista: %d’. % yhat[[0]) |
La ejecución del ejemplo se ajusta al modelo de conjunto subespacial aleatorio en todo el conjunto de datos y luego se utiliza para hacer una predicción en una nueva fila de datos, como podríamos hacer al utilizar el modelo en una aplicación.
Ahora que estamos familiarizados con el uso de bolsas para la clasificación, veamos el API para la regresión.
Conjunto subespacial aleatorio para la regresión
En esta sección, veremos el uso de la bolsa para un problema de regresión.
Primero, podemos usar la función make_regression() para crear un problema de regresión sintética con 1.000 ejemplos y 20 características de entrada.
El ejemplo completo figura a continuación.
|
# conjunto de datos de regresión de pruebas de sklearn.conjuntos de datos importación hacer_regresión # Definir el conjunto de datos X, y = make_regression(n_muestras=1000, n_funciones=20, n_informativo=15, ruido=0.1, estado_aleatorio=5) # resumir el conjunto de datos imprimir(X.forma, y.forma) |
Ejecutando el ejemplo se crea el conjunto de datos y se resume la forma de los componentes de entrada y salida.
A continuación, podemos evaluar un conjunto subespacial aleatorio a través de la bolsa de este conjunto de datos.
Como antes, debemos configurar el embolsado para utilizar todas las filas del conjunto de datos de entrenamiento y especificar el número de características de entrada a seleccionar al azar.
|
... # Definir el modelo modelo = BaggingRegressor(bootstrap=Falso, max_features=10) |
Como hicimos con la última sección, evaluaremos el modelo usando la validación cruzada repetida k-pliegue, con tres repeticiones y 10 pliegues. Informaremos del error medio absoluto (MAE) del modelo en todas las repeticiones y pliegues. La biblioteca de aprendizaje de ciencias hace que el MAE sea negativo, de modo que se maximiza en lugar de minimizarse. Esto significa que los MAE negativos más grandes son mejores y un modelo perfecto tiene un MAE de 0.
El ejemplo completo figura a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# Evaluar el conjunto subespacial aleatorio a través de la bolsa para la regresión de numpy importación significa de numpy importación std de sklearn.conjuntos de datos importación make_regression de sklearn.model_selection importación puntaje_valor_cruzado de sklearn.model_selection importación RepetidoKFold de sklearn.conjunto importación BaggingRegressor # Definir el conjunto de datos X, y = make_regression(n_muestras=1000, n_funciones=20, n_informativo=15, ruido=0.1, estado_aleatorio=5) # Definir el modelo modelo = BaggingRegressor(bootstrap=Falso, max_features=10) # Definir el procedimiento de evaluación cv = RepetidoKFold(n_splits=10, n_repeticiones=3, estado_aleatorio=1) # Evaluar el modelo n_puntuaciones = puntaje_valor_cruzado(modelo, X, y, puntuación=‘neg_mean_absolute_error’, cv=cv, n_jobs=–1, error_score=«aumentar) # Informe de rendimiento imprimir(MAE: %.3f (%.3f)’. % (significa(n_puntuaciones), std(n_puntuaciones))) |
La ejecución del ejemplo informa de la precisión de la media y la desviación estándar del modelo.
Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o el procedimiento de evaluación, o las diferencias en la precisión numérica. Considere ejecutar el ejemplo unas cuantas veces y compare el resultado promedio.
En este caso, podemos ver que el conjunto de bolsas con hiperparámetros predeterminados alcanza un MAE de alrededor de 114.
También podemos usar el modelo de conjunto subespacial aleatorio como modelo final y hacer predicciones para la regresión.
Primero, el conjunto se ajusta a todos los datos disponibles, luego se puede llamar a la función predict() para hacer predicciones sobre nuevos datos.
El siguiente ejemplo lo demuestra en nuestro conjunto de datos de regresión.
|
# Conjunto subespacial aleatorio a través de la bolsa para hacer predicciones de regresión de sklearn.conjuntos de datos importación make_regression de sklearn.conjunto importación BaggingRegressor # Definir el conjunto de datos X, y = make_regression(n_muestras=1000, n_funciones=20, n_informativo=15, ruido=0.1, estado_aleatorio=5) # Definir el modelo modelo = BaggingRegressor(bootstrap=Falso, max_features=10) # Encajar el modelo en todo el conjunto de datos modelo.encajar(X, y) # hacer una sola predicción fila = [[[[0.88950817,–0.93540416,0.08392824,0.26438806,–0.52828711,–1.21102238,–0.4499934,1.47392391,–0.19737726,–0.22252503,0.02307668,0.26953276,0.03572757,–0.51606983,–0.39937452,1.8121736,–0.00775917,–0.02514283,–0.76089365,1.58692212]] yhat = modelo.predecir(fila) imprimir(«Predicción: %d % yhat[[0]) |
La ejecución del ejemplo se ajusta al modelo de conjunto subespacial aleatorio en todo el conjunto de datos y luego se utiliza para hacer una predicción en una nueva fila de datos, como podríamos hacer al utilizar el modelo en una aplicación.
Ahora que estamos familiarizados con el uso de la API de scikit-learn para evaluar y usar conjuntos subespaciales aleatorios, veamos la configuración del modelo.
Conjunto subespacial aleatorio de hiperparámetros
En esta sección, examinaremos más de cerca algunos de los hiperparámetros que debería considerar para la sintonización del conjunto subespacial aleatorio y su efecto en el rendimiento del modelo.
Explorar el número de árboles
Un importante hiperparámetro para el método subespacial aleatorio es el número de árboles de decisión utilizados en el conjunto. Un mayor número de árboles estabilizará la varianza del modelo, contrarrestando el efecto del número de características seleccionadas por cada árbol que introduce la diversidad.
El número de árboles se puede establecer a través de la «n_estimadores«y por defecto a 10.
El siguiente ejemplo explora el efecto del número de árboles con valores entre 10 y 5.000.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
# Explorar el conjunto subespacial aleatorio número de árboles efecto en la actuación de numpy importación significa de numpy importación std de sklearn.conjuntos de datos importación make_classification de sklearn.model_selection importación puntaje_valor_cruzado de sklearn.model_selection importación RepeatedStratifiedKFold de sklearn.conjunto importación BaggingClassifier de matplotlib importación pyplot # Obtener el conjunto de datos def get_dataset(): X, y = make_classification(n_muestras=1000, n_funciones=20, n_informativo=15, n_redundante=5, estado_aleatorio=5) volver X, y # Obtener una lista de modelos para evaluar def get_models(): modelos = dict() n_árboles = [[10, 50, 100, 500, 1000, 5000] para n en n_árboles: modelos[[str(n)] = BaggingClassifier(n_estimadores=n, bootstrap=Falso, max_features=10) volver modelos # Evaluar un modelo dado usando validación cruzada def evaluate_model(modelo): cv = RepeatedStratifiedKFold(n_splits=10, n_repeticiones=3, estado_aleatorio=1) resultados = puntaje_valor_cruzado(modelo, X, y, puntuación=«exactitud, cv=cv, n_jobs=–1) volver resultados # Definir el conjunto de datos X, y = get_dataset() # conseguir que los modelos evalúen modelos = get_models() # Evaluar los modelos y almacenar los resultados resultados, nombres = lista(), lista() para nombre, modelo en modelos.artículos(): resultados = evaluate_model(modelo) resultados.anexar(resultados) nombres.anexar(nombre) imprimir(«>%s %.3f (%.3f) % (nombre, significa(resultados), std(resultados))) # Rendimiento del modelo de la trama para la comparación pyplot.Boxplot(resultados, etiquetas=nombres, showmeans=Verdadero) pyplot.mostrar() |
La ejecución del ejemplo primero reporta la precisión media para cada número configurado de árboles de decisión.
Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o el procedimiento de evaluación, o las diferencias en la precisión numérica. Considere ejecutar el ejemplo unas cuantas veces y compare el resultado promedio.
En este caso, podemos ver que ese rendimiento parece seguir mejorando a medida que el número de miembros del conjunto se incrementa a 5.000.
|
>10 0.853 (0.030) >50 0.885 (0.038) >100 0.891 (0.034) >500 0.894 (0.036) >1000 0.894 (0.034) >5000 0.896 (0.033) |
Se crea un gráfico de caja y bigote para la distribución de las puntuaciones de precisión para cada número configurado de árboles.
Podemos ver la tendencia general de una mayor mejora con el número de árboles de decisión utilizados en el conjunto.
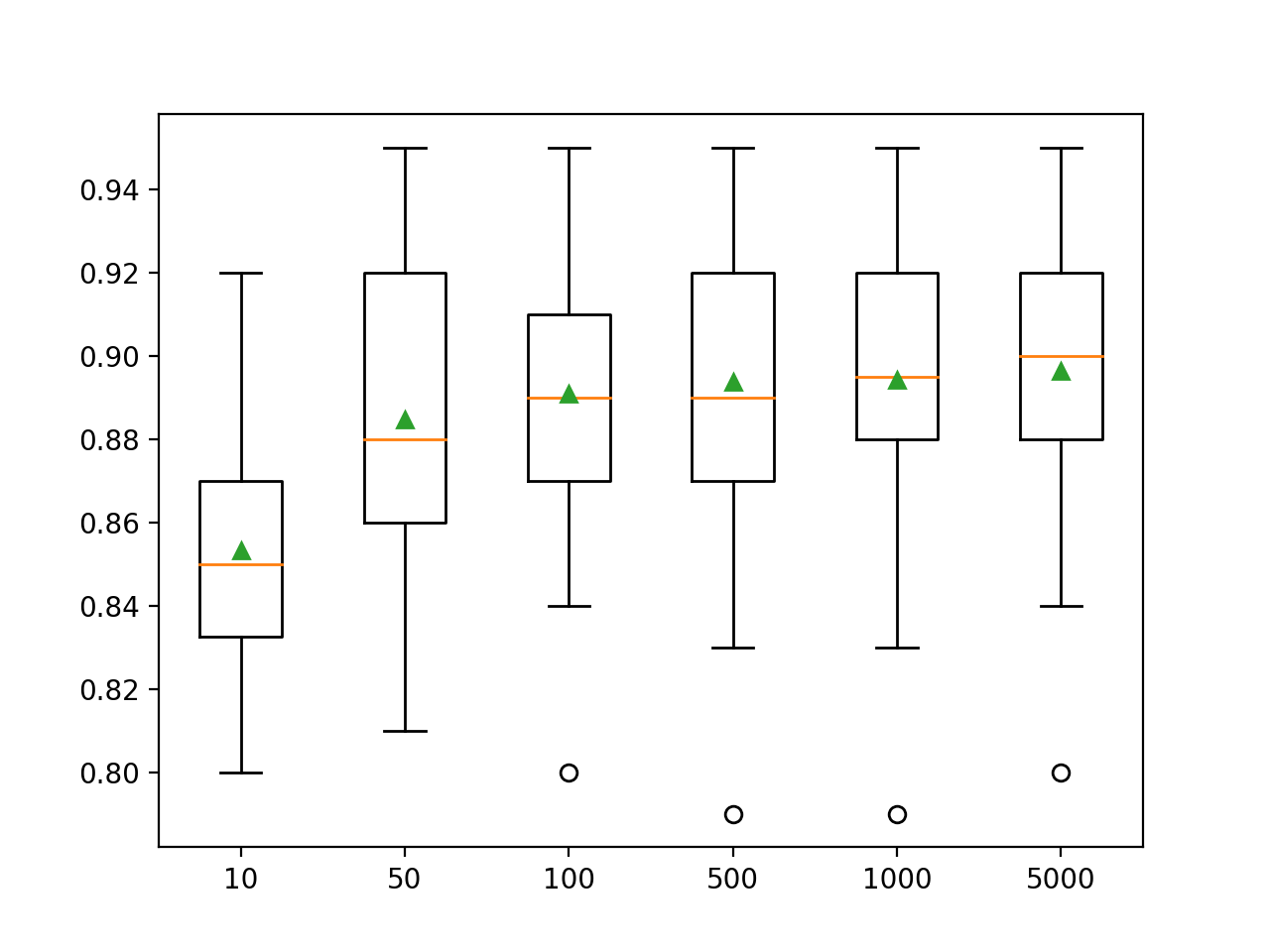
Cuadro del tamaño de un conjunto subespacial aleatorio vs. Precisión de la clasificación
Explorar el número de características
El número de características seleccionadas para cada subespacio aleatorio controla la diversidad del conjunto.
Menos rasgos significan más diversidad, mientras que más rasgos significan menos diversidad. Una mayor diversidad puede requerir más árboles para reducir la variabilidad de las predicciones hechas por el modelo.
Podemos variar la diversidad del conjunto variando el número de características aleatorias seleccionadas mediante el ajuste de la «max_features«argumento».
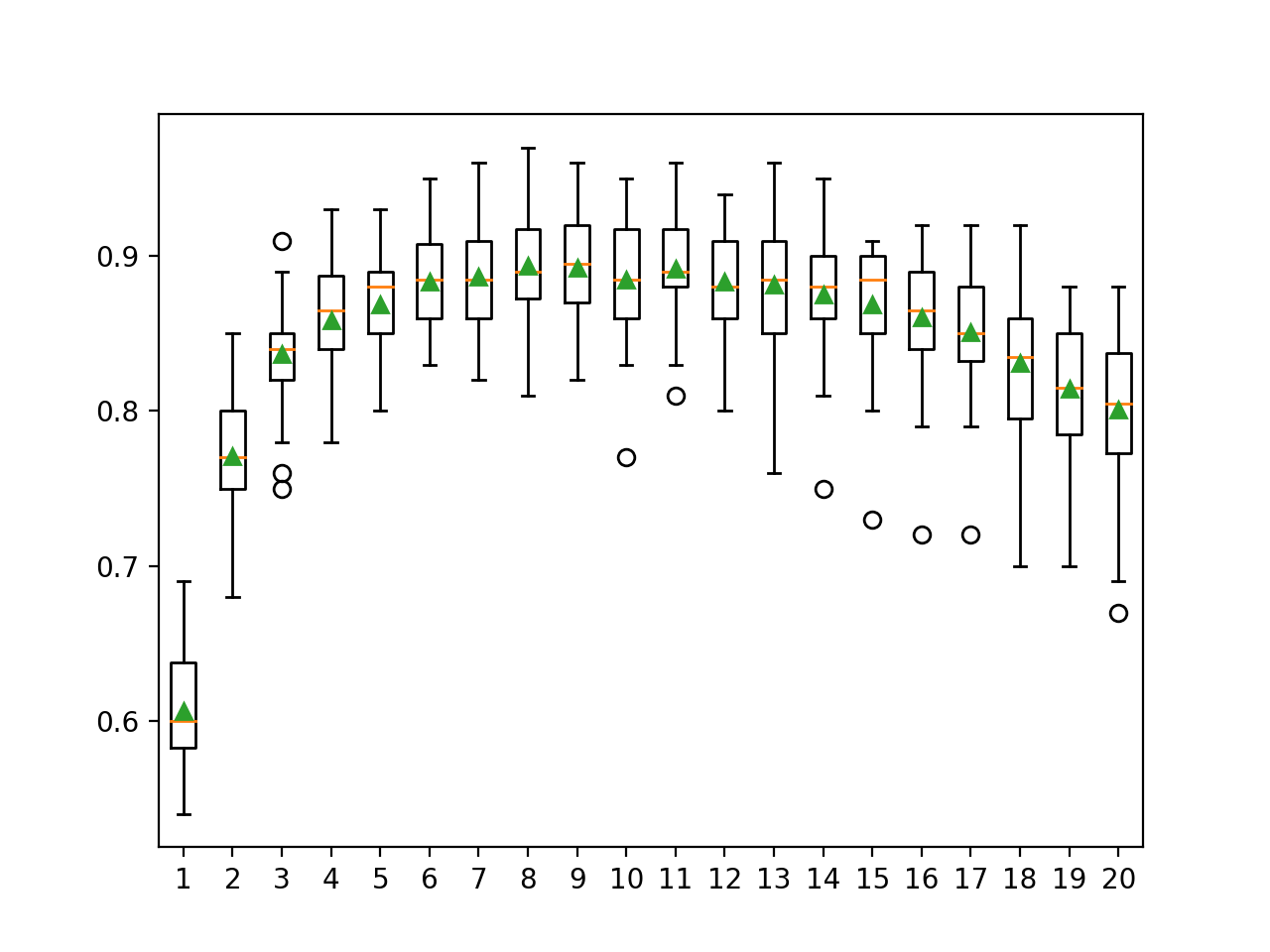
En el ejemplo siguiente el valor varía de 1 a 20 con un número fijo de árboles en el conjunto.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
# Explorar el conjunto subespacial aleatorio número de características efecto en la actuación de numpy importación significa de numpy importación std de sklearn.conjuntos de datos importación make_classification de sklearn.model_selection importación puntaje_valor_cruzado de sklearn.model_selection importación RepeatedStratifiedKFold de sklearn.conjunto importación BaggingClassifier de matplotlib importación pyplot # Obtener el conjunto de datos def get_dataset(): X, y = make_classification(n_muestras=1000, n_funciones=20, n_informativo=15, n_redundante=5, estado_aleatorio=5) volver X, y # Obtener una lista de modelos para evaluar def get_models(): modelos = dict() para n en rango(1,21): modelos[[str(n)] = BaggingClassifier(n_estimadores=100, bootstrap=Falso, max_features=n) volver modelos # Evaluar un modelo dado usando validación cruzada def evaluate_model(modelo): cv = RepeatedStratifiedKFold(n_splits=10, n_repeticiones=3, estado_aleatorio=1) resultados = puntaje_valor_cruzado(modelo, X, y, puntuación=«exactitud, cv=cv, n_jobs=–1) volver resultados # Definir el conjunto de datos X, y = get_dataset() # conseguir que los modelos evalúen modelos = get_models() # Evaluar los modelos y almacenar los resultados resultados, nombres = lista(), lista() para nombre, modelo en modelos.artículos(): resultados = evaluate_model(modelo) resultados.anexar(resultados) nombres.anexar(nombre) imprimir(«>%s %.3f (%.3f) % (nombre, significa(resultados), std(resultados))) # Rendimiento del modelo de la trama para la comparación pyplot.Boxplot(resultados, etiquetas=nombres, showmeans=Verdadero) pyplot.mostrar() |
Ejecutando el ejemplo primero se informa de la precisión media para cada número de características.
Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o el procedimiento de evaluación, o las diferencias en la precisión numérica. Considere ejecutar el ejemplo unas cuantas veces y compare el resultado promedio.
En este caso, podemos ver que quizás el uso de 8 a 11 características en los subespacios aleatorios podría ser apropiado en este conjunto de datos al utilizar 100 árboles de decisión. Esto podría sugerir que primero se aumente el número de árboles a un valor grande, y luego se ajuste el número de características seleccionadas en cada subconjunto.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
>1 0.607 (0.036) >2 0.771 (0.042) >3 0.837 (0.036) >4 0.858 (0.037) >5 0.869 (0.034) >6 0.883 (0.033) >7 0.887 (0.038) >8 0.894 (0.035) >9 0.893 (0.035) >10 0.885 (0.038) >11 0.892 (0.034) >12 0.883 (0.036) >13 0.881 (0.044) >14 0.875 (0.038) >15 0.869 (0.041) >16 0.861 (0.044) >17 0.851 (0.041) >18 0.831 (0.046) >19 0.815 (0.046) >20 0.801 (0.049) |
Se crea un gráfico de caja y bigote para la distribución de las puntuaciones de precisión para cada número de características de subconjuntos aleatorios.
Podemos ver una tendencia general de aumento de la precisión hasta un punto y una disminución constante del rendimiento después de 11 características.

Cuadro de características de un conjunto subespacial aleatorio vs. precisión de clasificación
Explorar el algoritmo alternativo
Los árboles de decisión son el algoritmo más común usado en un conjunto subespacial aleatorio.
La razón de esto es que son fáciles de configurar y funcionan bien en la mayoría de los problemas.
Pueden utilizarse otros algoritmos para construir subespacios aleatorios y deben configurarse para que tengan una varianza modestamente alta. Un ejemplo es el algoritmo de los vecinos más cercanos donde el k se puede ajustar a un valor bajo.
El algoritmo utilizado en el conjunto se especifica a través de la «base_estimador«y debe ser establecido en una instancia del algoritmo y la configuración del algoritmo a utilizar.
El siguiente ejemplo demuestra el uso de un KNeighborsClassifier como algoritmo base utilizado en el conjunto subespacial aleatorio a través de la clase «bagging». Aquí, el algoritmo se utiliza con hiperparámetros predeterminados donde k se establece en 5.
|
... # Definir el modelo modelo = BaggingClassifier(base_estimador=KNeighborsClassifier(), bootstrap=Falso, max_features=10) |
El ejemplo completo figura a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
# Evaluar el conjunto subespacial aleatorio con el algoritmo knn para la clasificación de numpy importación significa de numpy importación std de sklearn.conjuntos de datos importación make_classification de sklearn.model_selection importación puntaje_valor_cruzado de sklearn.model_selection importación RepeatedStratifiedKFold de sklearn.vecinos importación KNeighborsClassifier de sklearn.conjunto importación BaggingClassifier # Definir el conjunto de datos X, y = make_classification(n_muestras=1000, n_funciones=20, n_informativo=15, n_redundante=5, estado_aleatorio=5) # Definir el modelo modelo = BaggingClassifier(base_estimador=KNeighborsClassifier(), bootstrap=Falso, max_features=10) # Definir el procedimiento de evaluación cv = RepeatedStratifiedKFold(n_splits=10, n_repeticiones=3, estado_aleatorio=1) # Evaluar el modelo n_puntuaciones = puntaje_valor_cruzado(modelo, X, y, puntuación=«exactitud, cv=cv, n_jobs=–1, error_score=«aumentar) # Informe de rendimiento imprimir(«Precisión: %.3f (%.3f) % (significa(n_puntuaciones), std(n_puntuaciones))) |
La ejecución del ejemplo informa de la precisión de la media y la desviación estándar del modelo.
Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o el procedimiento de evaluación, o las diferencias en la precisión numérica. Considere ejecutar el ejemplo unas cuantas veces y compare el resultado promedio.
En este caso, podemos ver que el conjunto subespacial aleatorio con KNN e hiperparámetros por defecto logra una precisión de clasificación de alrededor del 90 por ciento en este conjunto de datos de prueba.
Más lecturas
Esta sección proporciona más recursos sobre el tema si desea profundizar en él.
Documentos
Libros
APIs
Artículos
Resumen
En este tutorial, descubriste cómo desarrollar conjuntos subespaciales aleatorios para la clasificación y la regresión.
Específicamente, aprendiste:
- Se crean conjuntos subespaciales aleatorios a partir de árboles de decisión que se ajustan a diferentes muestras de características (columnas) en el conjunto de datos de entrenamiento.
- Cómo usar el conjunto subespacial aleatorio para la clasificación y regresión con scikit-learn.
- Cómo explorar el efecto de los hiperparámetros de los modelos subespaciales aleatorios en el rendimiento de los modelos.
¿Tiene alguna pregunta?
Haga sus preguntas en los comentarios de abajo y haré lo posible por responder.
