
Búsqueda local iterada es un algoritmo de optimización global estocástico.
Implica la aplicación repetida de un algoritmo de búsqueda local a versiones modificadas de una buena solución encontrada anteriormente. De esta manera, es como una versión inteligente del algoritmo de escalada estocástica con reinicios aleatorios.
La intuición detrás del algoritmo es que los reinicios aleatorios pueden ayudar a localizar muchos óptimos locales en un problema y que los mejores óptimos locales suelen estar cerca de otros óptimos locales. Por lo tanto, las perturbaciones modestas de los óptimos locales existentes pueden encontrar mejores o incluso mejores soluciones para un problema de optimización.
En este tutorial, descubrirá cómo implementar el algoritmo de búsqueda local iterado desde cero.
Después de completar este tutorial, sabrá:
- La búsqueda local iterada es un algoritmo de optimización de búsqueda global estocástica que es una versión más inteligente de la escalada estocástica con reinicios aleatorios.
- Cómo implementar la escalada estocástica con reinicios aleatorios desde cero.
- Cómo implementar y aplicar el algoritmo de búsqueda local iterado a una función objetivo no lineal.
Empecemos.

Búsqueda local iterada desde cero en Python
Foto de Susanne Nilsson, algunos derechos reservados.
Descripción general del tutorial
Este tutorial se divide en cinco partes; Ellos son:
- ¿Qué es la búsqueda local iterada?
- Función objetivo de Ackley
- Algoritmo de escalada estocástico
- Escalada estocástica con reinicios aleatorios
- Algoritmo de búsqueda local iterado
¿Qué es la búsqueda local iterada?
La búsqueda local iterada, o ILS para abreviar, es un algoritmo estocástico de optimización de búsqueda global.
Está relacionado o es una extensión de la escalada estocástica y la escalada estocástica con inicios aleatorios.
Es esencialmente una versión más inteligente de Hill-Climbing con reinicios aleatorios.
– Página 26, Fundamentos de metaheurística, 2011.
La escalada estocástica es un algoritmo de búsqueda local que implica realizar modificaciones aleatorias a una solución existente y aceptar la modificación solo si da mejores resultados que la solución de trabajo actual.
Los algoritmos de búsqueda local en general pueden atascarse en los óptimos locales. Un enfoque para abordar este problema es reiniciar la búsqueda desde un nuevo punto de partida seleccionado al azar. El procedimiento de reinicio se puede realizar muchas veces y se puede activar después de un número fijo de evaluaciones de funciones o si no se observan mejoras adicionales para un número determinado de iteraciones del algoritmo. Este algoritmo se llama escalada estocástica con reinicios aleatorios.
La posibilidad más simple de mejorar un costo encontrado por LocalSearch es repetir la búsqueda desde otro punto de partida.
– Página 132, Manual de metaheurística, 3a edición de 2019.
La búsqueda local iterada es similar a la escalada estocástica con reinicios aleatorios, excepto que en lugar de seleccionar un punto de inicio aleatorio para cada reinicio, se selecciona un punto en función de una versión modificada del mejor punto encontrado hasta ahora durante la búsqueda más amplia.
La perturbación de la mejor solución hasta ahora es como un gran salto en el espacio de búsqueda a una nueva región, mientras que las perturbaciones provocadas por el algoritmo estocástico de escalada de colinas son mucho más pequeñas, confinadas a una región específica del espacio de búsqueda.
La heurística aquí es que a menudo puede encontrar mejores óptimos locales cerca de donde se encuentra actualmente, y caminar de un óptimo local a otro óptimo local de esta manera a menudo supera al probar nuevas ubicaciones completamente al azar.
– Página 26, Fundamentos de metaheurística, 2011.
Esto permite que la búsqueda se realice en dos niveles. El algoritmo de escalada es la búsqueda local para aprovechar al máximo una solución candidata específica o región del espacio de búsqueda, y el enfoque de reinicio permite explorar diferentes regiones del espacio de búsqueda.
De esta forma, el algoritmo Iterated Local Search explora múltiples óptimos locales en el espacio de búsqueda, aumentando la probabilidad de localizar los óptimos globales.
La Búsqueda Local Iterada se propuso para problemas de optimización combinatoria, como el problema del viajante de comercio (TSP), aunque se puede aplicar a la optimización de funciones continuas utilizando diferentes tamaños de paso en el espacio de búsqueda: pasos más pequeños para la subida de colinas y pasos más grandes para el reinicio aleatorio.
Ahora que estamos familiarizados con el algoritmo de búsqueda local iterada, exploremos cómo implementar el algoritmo desde cero.
Función objetivo de Ackley
Primero, definamos un problema de optimización de canalización como base para implementar el algoritmo de búsqueda local iterada.
La función Ackley es un ejemplo de una función objetivo multimodal que tiene un único óptimo global y múltiples óptimos locales en los que una búsqueda local puede atascarse.
Como tal, se requiere una técnica de optimización global. Es una función objetivo bidimensional que tiene un óptimo global en [0,0], que se evalúa como 0.0.
El siguiente ejemplo implementa el Ackley y crea un gráfico de superficie tridimensional que muestra los óptimos globales y múltiples óptimos locales.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
# función multimodal ackley desde numpy importar arange desde numpy importar Exp desde numpy importar sqrt desde numpy importar porque desde numpy importar mi desde numpy importar Pi desde numpy importar rejilla desde matplotlib importar pyplot desde mpl_toolkits.mplot3d importar Ejes3D # función objetiva def objetivo(X, y): regreso –20,0 * Exp(–0,2 * sqrt(0,5 * (X**2 + y **2))) – Exp(0,5 * (porque(2 * Pi * X) + porque(2 * Pi * y))) + mi + 20 # definir rango para entrada r_min, r_max = –5,0, 5,0 # rango de entrada de muestra uniformemente en incrementos de 0.1 xaxis = arange(r_min, r_max, 0,1) yaxis = arange(r_min, r_max, 0,1) # crea una malla a partir del eje X, y = rejilla(xaxis, yaxis) # calcular objetivos resultados = objetivo(X, y) # crea un gráfico de superficie con el esquema de color jet figura = pyplot.figura() eje = figura.gca(proyección=‘3d’) eje.plot_surface(X, y, resultados, cmap=‘chorro’) # mostrar la trama pyplot.show() |
La ejecución del ejemplo crea el gráfico de superficie de la función Ackley que muestra la gran cantidad de óptimos locales.
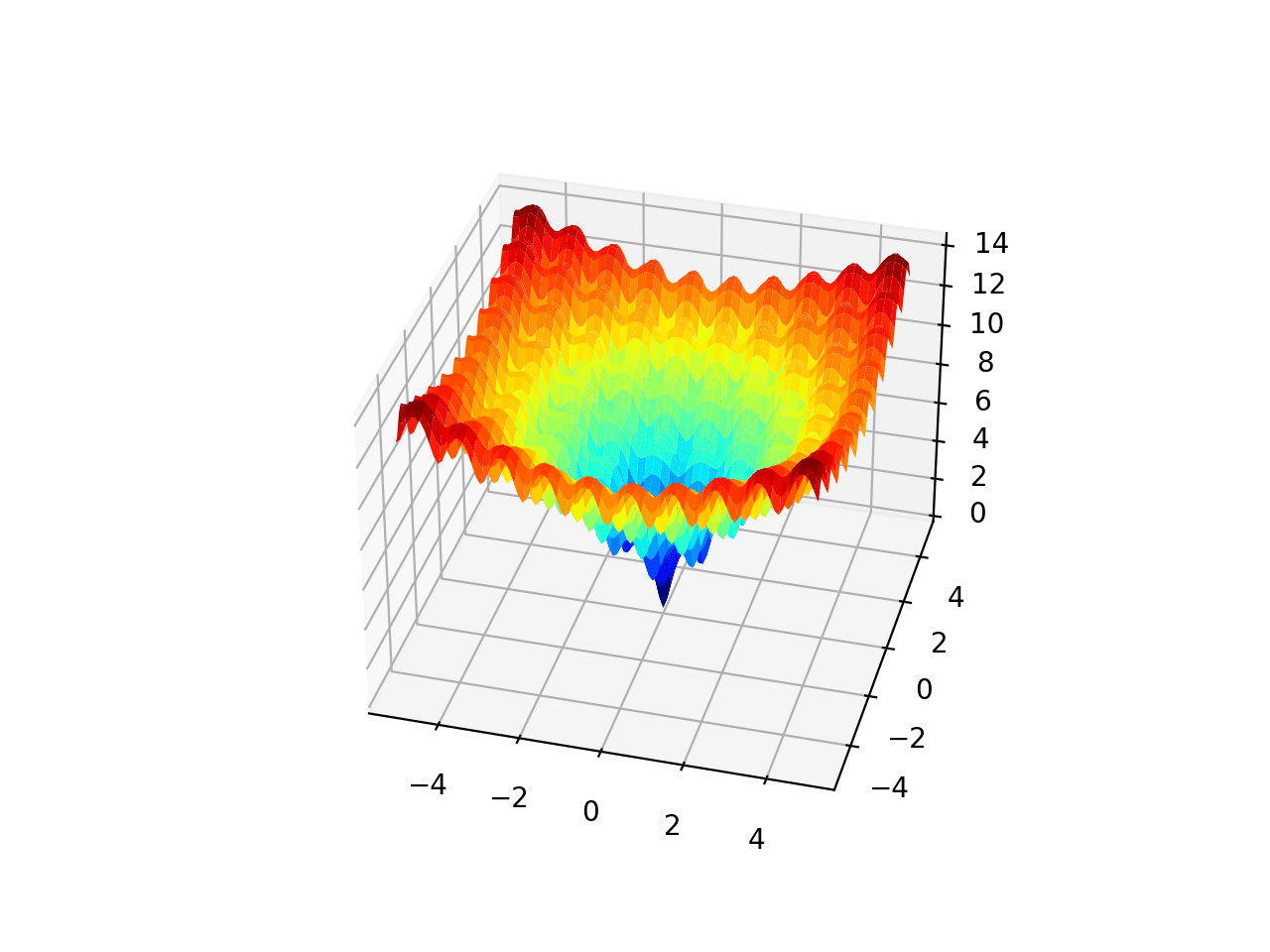
Gráfico de superficie 3D de la función multimodal de Ackley
Usaremos esto como base para implementar y comparar un algoritmo simple de escalada estocástica, escalada estocástica con reinicios aleatorios y, finalmente, búsqueda local iterada.
Es de esperar que un algoritmo estocástico de escalada de colinas se atasque fácilmente en los mínimos locales. Esperaríamos que la escalada estocástica con reinicios encontrara muchos mínimos locales, y esperaríamos que la búsqueda local iterada se desempeñara mejor que cualquier método en este problema si se configura adecuadamente.
Algoritmo de escalada estocástico
El núcleo del algoritmo de búsqueda local iterada es una búsqueda local y, en este tutorial, utilizaremos el algoritmo de escalada estocástica para este propósito.
El algoritmo Stochastic Hill Climbing implica generar primero un punto de partida aleatorio y una solución de trabajo actual, luego generar versiones perturbadas de la solución de trabajo actual y aceptarlas si son mejores que la solución de trabajo actual.
Dado que estamos trabajando en un problema de optimización continua, una solución es un vector de valores a evaluar por la función objetivo, en este caso, un punto en un espacio bidimensional acotado por -5 y 5.
Podemos generar un punto aleatorio muestreando el espacio de búsqueda con una distribución de probabilidad uniforme. Por ejemplo:
|
... # generar un punto aleatorio en el espacio de búsqueda solución = límites[[:, 0] + rand(len(límites)) * (límites[[:, 1] – límites[[:, 0]) |
Podemos generar versiones perturbadas de una solución que funciona actualmente usando una distribución de probabilidad gaussiana con la media de los valores actuales en la solución y una desviación estándar controlada por un hiperparámetro que controla qué tan lejos se permite explorar la búsqueda desde la solución de trabajo actual.
Nos referiremos a este hiperparámetro como «Numero de pie«, por ejemplo:
|
... # generar una versión perturbada de una solución de trabajo actual candidato = solución + randn(len(límites)) * Numero de pie |
Es importante destacar que debemos comprobar que las soluciones generadas se encuentran dentro del espacio de búsqueda.
Esto se puede lograr con una función personalizada llamada dentro_límites () que toma una solución candidata y los límites del espacio de búsqueda y devuelve Verdadero si el punto está en el espacio de búsqueda, Falso de lo contrario.
|
# comprobar si un punto está dentro de los límites de la búsqueda def in_bounds(punto, límites): # enumere todas las dimensiones del punto por D en distancia(len(límites)): # comprobar si está fuera de los límites de esta dimensión si punto[[D] < límites[[D, 0] o punto[[D] > límites[[D, 1]: regreso Falso regreso Cierto |
Esta función se puede llamar durante la subida de la colina para confirmar que hay nuevos puntos dentro de los límites del espacio de búsqueda y, de lo contrario, se pueden generar nuevos puntos.
Uniendo esto, la función Montañismo() a continuación implementa el algoritmo de búsqueda local estocástico de escalada de colinas. Toma el nombre de la función objetivo, los límites del problema, el número de iteraciones y el tamaño de los pasos como argumentos y devuelve la mejor solución y su evaluación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 |
# algoritmo de búsqueda local de escalada def Montañismo(objetivo, límites, n_iteraciones, Numero de pie): # generar un punto inicial solución = Ninguno tiempo solución es Ninguno o no in_bounds(solución, límites): solución = límites[[:, 0] + rand(len(límites)) * (límites[[:, 1] – límites[[:, 0]) # evaluar el punto inicial solution_eval = objetivo(solución) # corre la subida de la colina por I en distancia(n_iteraciones): # Da un paso candidato = Ninguno tiempo candidato es Ninguno o no in_bounds(candidato, límites): candidato = solución + randn(len(límites)) * paso_Talla # evaluar el punto candidato candidte_eval = objetivo(candidato) # comprobar si debemos mantener el nuevo punto si candidte_eval <= solution_eval: # almacenar el nuevo punto solución, solution_eval = candidato, sincero_eval # informe de progreso imprimir(‘>% d f (% s) =% .5f’ % (I, solución, solution_eval)) regreso [[solución, solution_eval] |
Podemos probar este algoritmo en la función de Ackley.
Arreglaremos la semilla para el generador de números pseudoaleatorios para asegurarnos de obtener los mismos resultados cada vez que se ejecuta el código.
El algoritmo se ejecutará durante 1000 iteraciones y se utilizará un tamaño de paso de 0,05 unidades; Ambos hiperparámetros fueron elegidos después de un pequeño ensayo y error.
Al final de la ejecución, informaremos sobre la mejor solución encontrada.
|
... # siembra el generador de números pseudoaleatorios semilla(1) # definir rango para entrada límites = asarray([[[[–5,0, 5,0], [[–5,0, 5,0]]) # definir las iteraciones totales n_iteraciones = 1000 # definir el tamaño máximo de paso Numero de pie = 0,05 # realizar la búsqueda de escalada mejor, puntaje = Montañismo(objetivo, límites, n_iteraciones, Numero de pie) imprimir(‘¡Hecho!’) imprimir(‘f (% s) =% f’ % (mejor, puntaje)) |
Al unir esto, el ejemplo completo de la aplicación del algoritmo estocástico de escalada de colinas a la función objetivo de Ackley se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 |
# búsqueda de escalada de la función objetivo ackley desde numpy importar asarray desde numpy importar Exp desde numpy importar sqrt desde numpy importar porque desde numpy importar mi desde numpy importar Pi desde numpy.aleatorio importar randn desde numpy.aleatorio importar rand desde numpy.aleatorio importar semilla # función objetiva def objetivo(v): X, y = v regreso –20,0 * Exp(–0,2 * sqrt(0,5 * (X**2 + y **2))) – Exp(0,5 * (porque(2 * Pi * X) + porque(2 * Pi * y))) + mi + 20 # comprobar si un punto está dentro de los límites de la búsqueda def in_bounds(punto, límites): # enumere todas las dimensiones del punto por D en distancia(len(límites)): # comprobar si está fuera de los límites de esta dimensión si punto[[D] < límites[[D, 0] o punto[[D] > límites[[D, 1]: regreso Falso regreso Cierto # algoritmo de búsqueda local de escalada def Montañismo(objetivo, límites, n_iteraciones, Numero de pie): # generar un punto inicial solución = Ninguno tiempo solución es Ninguno o no in_bounds(solución, límites): solución = límites[[:, 0] + rand(len(límites)) * (límites[[:, 1] – límites[[:, 0]) # evaluar el punto inicial solution_eval = objetivo(solución) # corre la subida de la colina por I en distancia(n_iteraciones): # Da un paso candidato = Ninguno tiempo candidato es Ninguno o no in_bounds(candidato, límites): candidato = solución + randn(len(límites)) * paso_Talla # evaluar el punto candidato candidte_eval = objetivo(candidato) # comprobar si debemos mantener el nuevo punto si candidte_eval <= solution_eval: # almacenar el nuevo punto solución, solution_eval = candidato, sincero_eval # informe de progreso imprimir(‘>% d f (% s) =% .5f’ % (I, solución, solution_eval)) regreso [[solución, solution_eval] # siembra el generador de números pseudoaleatorios semilla(1) # definir rango para entrada límites = asarray([[[[–5,0, 5,0], [[–5,0, 5,0]]) # definir las iteraciones totales n_iteraciones = 1000 # definir el tamaño máximo de paso Numero de pie = 0,05 # realizar la búsqueda de escalada mejor, puntaje = Montañismo(objetivo, límites, n_iteraciones, Numero de pie) imprimir(‘¡Hecho!’) imprimir(‘f (% s) =% f’ % (mejor, puntaje)) |
Al ejecutar el ejemplo, se realiza la búsqueda estocástica de escalada en la función objetivo. Cada mejora encontrada durante la búsqueda se informa y luego se informa la mejor solución al final de la búsqueda.
Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o procedimiento de evaluación, o las diferencias en la precisión numérica. Considere ejecutar el ejemplo varias veces y compare el resultado promedio.
En este caso, podemos ver alrededor de 13 mejoras durante la búsqueda y una solución final de aproximadamente f (-0,981, 1,965), lo que da como resultado una evaluación de aproximadamente 5,381, que está lejos de f (0,0, 0,0) = 0.
|
> 0 f ([-0.85618854 2.1495965 ]) = 6,46986 > 1 f ([-0.81291816 2.03451957]) = 6,07149 > 5 f ([-0.82903902 2.01531685]) = 5,93526 > 7 f ([-0.83766043 1.97142393]) = 5,82047 > 9 f ([-0.89269139 2.02866012]) = 5,68283 > 12 f ([-0.8988359 1.98187164]) = 5,55899 > 13 f ([-0.9122303 2.00838942]) = 5.55566 > 14 f ([-0.94681334 1.98855174]) = 5,43024 > 15 f ([-0.98117198 1.94629146]) = 5.39010 > 23 f ([-0.97516403 1.97715161]) = 5.38735 > 39 f ([-0.98628044 1.96711371]) = 5.38241 > 362 f ([-0.9808789 1.96858459]) = 5.38233 > 629 f ([-0.98102417 1.96555308]) = 5.38194 ¡Hecho! F([-0.98102417 1.96555308]) = 5.381939 |
A continuación, modificaremos el algoritmo para realizar reinicios aleatorios y veremos si podemos lograr mejores resultados.
Escalada estocástica con reinicios aleatorios
El algoritmo Stochastic Hill Climbing With Random Restarts implica la ejecución repetida del algoritmo Stochastic Hill Climbing y realizar un seguimiento de la mejor solución encontrada.
Primero, modifiquemos el Montañismo() función para tomar el punto de partida de la búsqueda en lugar de generarla aleatoriamente. Esto ayudará más adelante cuando implementemos el algoritmo de búsqueda local iterada más adelante.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 |
# algoritmo de búsqueda local de escalada def Montañismo(objetivo, límites, n_iteraciones, Numero de pie, start_pt): # almacenar el punto inicial solución = comienzo_pt # evaluar el punto inicial solution_eval = objetivo(solución) # corre la subida de la colina por I en distancia(n_iteraciones): # Da un paso candidato = Ninguno tiempo candidato es Ninguno o no in_bounds(candidato, límites): candidato = solución + randn(len(límites)) * paso_Talla # evaluar el punto candidato candidte_eval = objetivo(candidato) # comprobar si debemos mantener el nuevo punto si candidte_eval <= solution_eval: # almacenar el nuevo punto solución, solution_eval = candidato, candidte_eval regreso [[solución, solution_eval] |
A continuación, podemos implementar el algoritmo de reinicio aleatorio llamando repetidamente al Montañismo() funcionar un número fijo de veces.
En cada llamada, generaremos un nuevo punto de partida seleccionado al azar para la búsqueda de escalada.
|
... # generar un punto inicial aleatorio para la búsqueda start_pt = Ninguno tiempo start_pt es Ninguno o no in_bounds(start_pt, límites): start_pt = límites[[:, 0] + rand(len(límites)) * (límites[[:, 1] – límites[[:, 0]) # realizar una búsqueda estocástica de escalada solución, solution_eval = Montañismo(objetivo, límites, nitro, Numero de pie, start_pt) |
We can then inspect the result and keep it if it is better than any result of the search we have seen so far.
|
... # check for new best if solution_eval < best_eval: best, best_eval = solution, solution_eval print(‘Restart %d, best: f(%s) = %.5f’ % (n, best, best_eval)) |
Tying this together, the random_restarts() function implemented the stochastic hill climbing algorithm with random restarts.
|
# hill climbing with random restarts algorithm def random_restarts(objective, bounds, n_iter, step_size, n_restarts): best, best_eval = None, 1e+10 # enumerate restarts por n in range(n_restarts): # generate a random initial point for the search start_pt = None while start_pt es None o not in_bounds(start_pt, bounds): start_pt = bounds[[:, 0] + rand(len(bounds)) * (bounds[[:, 1] – bounds[[:, 0]) # perform a stochastic hill climbing search solution, solution_eval = hillclimbing(objective, bounds, n_iter, step_size, start_pt) # check for new best if solution_eval < best_eval: best, best_eval = solution, solution_eval print(‘Restart %d, best: f(%s) = %.5f’ % (n, best, best_eval)) return [[best, best_eval] |
We can then apply this algorithm to the Ackley objective function. In this case, we will limit the number of random restarts to 30, chosen arbitrarily.
The complete example is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 sesenta y cinco 66 67 68 69 70 71 72 73 74 75 76 |
# hill climbing search with random restarts of the ackley objective function from numpy import asarray from numpy import exp from numpy import sqrt from numpy import cos from numpy import e from numpy import pi from numpy.random import randn from numpy.random import rand from numpy.random import seed # objective function def objective(v): x, y = v return –20.0 * exp(–0.2 * sqrt(0.5 * (x**2 + y**2))) – exp(0.5 * (cos(2 * pi * x) + cos(2 * pi * y))) + e + 20 # check if a point is within the bounds of the search def in_bounds(point, bounds): # enumerate all dimensions of the point por d in range(len(bounds)): # check if out of bounds for this dimension if point[[d] < bounds[[d, 0] o point[[d] > bounds[[d, 1]: return False return True # hill climbing local search algorithm def hillclimbing(objective, bounds, n_iterations, step_size, start_pt): # store the initial point solution = start_pt # evaluate the initial point solution_eval = objective(solution) # run the hill climb por I in range(n_iterations): # take a step candidate = None while candidate es None o not in_bounds(candidate, bounds): candidate = solution + randn(len(bounds)) * step_size # evaluate candidate point candidte_eval = objective(candidate) # check if we should keep the new point if candidte_eval <= solution_eval: # store the new point solution, solution_eval = candidate, candidte_eval return [[solution, solution_eval] # hill climbing with random restarts algorithm def random_restarts(objective, bounds, n_iter, step_size, n_restarts): best, best_eval = None, 1e+10 # enumerate restarts por n in range(n_restarts): # generate a random initial point for the search start_pt = None while start_pt es None o not in_bounds(start_pt, bounds): start_pt = bounds[[:, 0] + rand(len(bounds)) * (bounds[[:, 1] – bounds[[:, 0]) # perform a stochastic hill climbing search solution, solution_eval = hillclimbing(objective, bounds, n_iter, step_size, start_pt) # check for new best if solution_eval < best_eval: best, best_eval = solution, solution_eval print(‘Restart %d, best: f(%s) = %.5f’ % (n, best, best_eval)) return [[best, best_eval] # seed the pseudorandom number generator seed(1) # define range for input bounds = asarray([[[[–5.0, 5.0], [[–5.0, 5.0]]) # define the total iterations n_iter = 1000 # define the maximum step size step_size = 0.05 # total number of random restarts n_restarts = 30 # perform the hill climbing search best, score = random_restarts(objective, bounds, n_iter, step_size, n_restarts) print(‘Done!’) print(‘f(%s) = %f’ % (best, score)) |
Running the example will perform a stochastic hill climbing with random restarts search for the Ackley objective function. Each time an improved overall solution is discovered, it is reported and the final best solution found by the search is summarized.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, we can see three improvements during the search and that the best solution found was approximately f(0.002, 0.002), which evaluated to about 0.009, which is much better than a single run of the hill climbing algorithm.
|
Restart 0, best: f([-0.98102417 1.96555308]) = 5.38194 Restart 2, best: f([1.96522236 0.98120013]) = 5.38191 Restart 4, best: f([0.00223194 0.00258853]) = 0.00998 Done! f([0.00223194 0.00258853]) = 0.009978 |
Next, let’s look at how we can implement the iterated local search algorithm.
Iterated Local Search Algorithm
The Iterated Local Search algorithm is a modified version of the stochastic hill climbing with random restarts algorithm.
The important difference is that the starting point for each application of the stochastic hill climbing algorithm is a perturbed version of the best point found so far.
We can implement this algorithm by using the random_restarts() function as a starting point. Each restart iteration, we can generate a modified version of the best solution found so far instead of a random starting point.
This can be achieved by using a step size hyperparameter, much like is used in the stochastic hill climber. In this case, a larger step size value will be used given the need for larger perturbations in the search space.
|
... # generate an initial point as a perturbed version of the last best start_pt = None while start_pt es None o not in_bounds(start_pt, bounds): start_pt = best + randn(len(bounds)) * p_size |
Tying this together, the iterated_local_search() function is defined below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 |
# iterated local search algorithm def iterated_local_search(objective, bounds, n_iter, step_size, n_restarts, p_size): # define starting point best = None while best es None o not in_bounds(best, bounds): best = bounds[[:, 0] + rand(len(bounds)) * (bounds[[:, 1] – bounds[[:, 0]) # evaluate current best point best_eval = objective(best) # enumerate restarts por n in range(n_restarts): # generate an initial point as a perturbed version of the last best start_pt = None while start_pt es None o not in_bounds(start_pt, bounds): start_pt = best + randn(len(bounds)) * p_size # perform a stochastic hill climbing search solution, solution_eval = hillclimbing(objective, bounds, n_iter, step_size, start_pt) # check for new best if solution_eval < best_eval: best, best_eval = solution, solution_eval print(‘Restart %d, best: f(%s) = %.5f’ % (n, best, best_eval)) return [[best, best_eval] |
We can then apply the algorithm to the Ackley objective function. In this case, we will use a larger step size value of 1.0 for the random restarts, chosen after a little trial and error.
The complete example is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 sesenta y cinco 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 |
# iterated local search of the ackley objective function from numpy import asarray from numpy import exp from numpy import sqrt from numpy import cos from numpy import e from numpy import pi from numpy.random import randn from numpy.random import rand from numpy.random import seed # objective function def objective(v): x, y = v return –20.0 * exp(–0.2 * sqrt(0.5 * (x**2 + y**2))) – exp(0.5 * (cos(2 * pi * x) + cos(2 * pi * y))) + e + 20 # check if a point is within the bounds of the search def in_bounds(point, bounds): # enumerate all dimensions of the point por d in range(len(bounds)): # check if out of bounds for this dimension if point[[d] < bounds[[d, 0] o point[[d] > bounds[[d, 1]: return False return True # hill climbing local search algorithm def hillclimbing(objective, bounds, n_iterations, step_size, start_pt): # store the initial point solution = start_pt # evaluate the initial point solution_eval = objective(solution) # run the hill climb por I in range(n_iterations): # take a step candidate = None while candidate es None o not in_bounds(candidate, bounds): candidate = solution + randn(len(bounds)) * step_size # evaluate candidate point candidte_eval = objective(candidate) # check if we should keep the new point if candidte_eval <= solution_eval: # store the new point solution, solution_eval = candidate, candidte_eval return [[solution, solution_eval] # iterated local search algorithm def iterated_local_search(objective, bounds, n_iter, step_size, n_restarts, p_size): # define starting point best = None while best es None o not in_bounds(best, bounds): best = bounds[[:, 0] + rand(len(bounds)) * (bounds[[:, 1] – bounds[[:, 0]) # evaluate current best point best_eval = objective(best) # enumerate restarts por n in range(n_restarts): # generate an initial point as a perturbed version of the last best start_pt = None while start_pt es None o not in_bounds(start_pt, bounds): start_pt = best + randn(len(bounds)) * p_size # perform a stochastic hill climbing search solution, solution_eval = hillclimbing(objective, bounds, n_iter, step_size, start_pt) # check for new best if solution_eval < best_eval: best, best_eval = solution, solution_eval print(‘Restart %d, best: f(%s) = %.5f’ % (n, best, best_eval)) return [[best, best_eval] # seed the pseudorandom number generator seed(1) # define range for input bounds = asarray([[[[–5.0, 5.0], [[–5.0, 5.0]]) # define the total iterations n_iter = 1000 # define the maximum step size s_size = 0.05 # total number of random restarts n_restarts = 30 # perturbation step size p_size = 1.0 # perform the hill climbing search best, score = iterated_local_search(objective, bounds, n_iter, s_size, n_restarts, p_size) print(‘Done!’) print(‘f(%s) = %f’ % (best, score)) |
Running the example will perform an Iterated Local Search of the Ackley objective function.
Each time an improved overall solution is discovered, it is reported and the final best solution found by the search is summarized at the end of the run.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, we can see four improvements during the search and that the best solution found was two very small inputs that are close to zero, which evaluated to about 0.0003, which is better than either a single run of the hill climber or the hill climber with restarts.
|
Restart 0, best: f([-0.96775653 0.96853129]) = 3.57447 Restart 3, best: f([-4.50618519e-04 9.51020713e-01]) = 2.57996 Restart 5, best: f([ 0.00137423 -0.00047059]) = 0.00416 Restart 22, best: f([ 1.16431936e-04 -3.31358206e-06]) = 0.00033 Done! f([ 1.16431936e-04 -3.31358206e-06]) = 0.000330 |
Further Reading
This section provides more resources on the topic if you are looking to go deeper.
Books
Articles
Resumen
In this tutorial, you discovered how to implement the iterated local search algorithm from scratch.
Specifically, you learned:
- Iterated local search is a stochastic global search optimization algorithm that is a smarter version of stochastic hill climbing with random restarts.
- How to implement stochastic hill climbing with random restarts from scratch.
- How to implement and apply the iterated local search algorithm to a nonlinear objective function.
Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.
