La optimización de funciones requiere la selección de un algoritmo para muestrear eficientemente el espacio de búsqueda y localizar una buena o la mejor solución.
Hay muchos algoritmos para elegir, aunque es importante establecer una línea de base para los tipos de soluciones que son factibles o posibles para un problema. Esto se puede lograr utilizando un algoritmo de optimización ingenuo, como un búsqueda aleatoria o un búsqueda de cuadrícula.
Los resultados logrados por un algoritmo de optimización ingenuo son computacionalmente eficientes para generar y proporcionar un punto de comparación para algoritmos de optimización más sofisticados. A veces, se encuentra que los algoritmos ingenuos logran el mejor rendimiento, particularmente en aquellos problemas que son ruidosos o no son suaves y aquellos problemas en los que la experiencia en el dominio típicamente sesga la elección del algoritmo de optimización.
En este tutorial, descubrirá algoritmos ingenuos para la optimización de funciones.
Después de completar este tutorial, sabrá:
- El papel de los algoritmos ingenuos en los proyectos de optimización de funciones.
- Cómo generar y evaluar una búsqueda aleatoria para la optimización de funciones.
- Cómo generar y evaluar una búsqueda de cuadrícula para la optimización de funciones.
Empecemos.

Búsqueda aleatoria y búsqueda de cuadrícula para la optimización de funciones
Foto de Kosala Bandara, algunos derechos reservados.
Descripción general del tutorial
Este tutorial se divide en tres partes; son:
- Algoritmos ingenuos de optimización de funciones
- Búsqueda aleatoria para optimización de funciones
- Búsqueda de cuadrícula para optimización de funciones
Algoritmos ingenuos de optimización de funciones
Hay muchos algoritmos diferentes que puede utilizar para la optimización, pero ¿cómo saber si los resultados que obtiene son buenos?
Un enfoque para resolver este problema es establecer una línea de base en el rendimiento utilizando un algoritmo de optimización ingenuo.
Un algoritmo de optimización ingenuo es un algoritmo que no asume nada sobre la función objetivo que se está optimizando.
Se puede aplicar con muy poco esfuerzo y el mejor resultado obtenido por el algoritmo se puede utilizar como punto de referencia para comparar algoritmos más sofisticados. Si un algoritmo más sofisticado no puede lograr un mejor resultado que un algoritmo ingenuo en promedio, entonces no tiene habilidad en su problema y debe abandonarse.
Hay dos algoritmos ingenuos que se pueden utilizar para la optimización de funciones; son:
- Búsqueda aleatoria
- Búsqueda de cuadrícula
Estos algoritmos se denominan «buscar”Algoritmos porque, en la base, la optimización puede enmarcarse como un problema de búsqueda. P.ej. encuentre las entradas que minimizan o maximizan la salida de la función objetivo.
Existe otro algoritmo que se puede utilizar llamado «búsqueda exhaustiva» que enumera todas las entradas posibles. Esto rara vez se usa en la práctica, ya que no es factible enumerar todos los insumos posibles, p. Ej. requeriría demasiado tiempo para ejecutarse.
Sin embargo, si se encuentra trabajando en un problema de optimización para el cual todas las entradas se pueden enumerar y evaluar en un tiempo razonable, esta debería ser la estrategia predeterminada que debe utilizar.
Echemos un vistazo más de cerca a cada uno de ellos.
Búsqueda aleatoria para optimización de funciones
La búsqueda aleatoria también se conoce como optimización aleatoria o muestreo aleatorio.
La búsqueda aleatoria implica generar y evaluar entradas aleatorias a la función objetivo. Es eficaz porque no asume nada sobre la estructura de la función objetivo. Esto puede ser beneficioso para problemas en los que hay mucha experiencia en el dominio que puede influir o sesgar la estrategia de optimización, lo que permite descubrir soluciones no intuitivas.
… Muestreo aleatorio, que simplemente extrae m muestras aleatorias sobre el espacio de diseño utilizando un generador de números pseudoaleatorios. Para generar una muestra aleatoria x, podemos muestrear cada variable independientemente de una distribución.
– Página 236, Algoritmos de optimización, 2019.
La búsqueda aleatoria también puede ser la mejor estrategia para problemas muy complejos con áreas ruidosas o no uniformes (discontinuas) del espacio de búsqueda que pueden generar algoritmos que dependen de gradientes confiables.
Podemos generar una muestra aleatoria de un dominio usando un generador de números pseudoaleatorios. Cada variable requiere un límite o rango bien definido y se puede muestrear un valor aleatorio uniforme del rango y luego evaluarlo.
Generar muestras aleatorias es trivial desde el punto de vista computacional y no ocupa mucha memoria, por lo tanto, puede ser eficiente generar una muestra grande de entradas y luego evaluarlas. Cada muestra es independiente, por lo que las muestras se pueden evaluar en paralelo si es necesario para acelerar el proceso.
El siguiente ejemplo da un ejemplo de una función de objetivo de minimización unidimensional simple y genera y luego evalúa una muestra aleatoria de 100 entradas. A continuación, se informa la entrada con el mejor rendimiento.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 |
# ejemplo de búsqueda aleatoria para optimización de funciones desde numpy.aleatorio importar rand # función objetiva def objetivo(X): regreso X**2.0 # definir rango para entrada r_min, r_max = –5,0, 5,0 # generar una muestra aleatoria del dominio muestra = r_min + rand(100) * (r_max – r_min) # evaluar la muestra sample_eval = objetivo(muestra) # localizar la mejor solución best_ix = 0 por I en abarcar(len(muestra)): si sample_eval[[I] < sample_eval[[best_ix]: best_ix = I # resumir la mejor solución imprimir(‘Mejor: f (%. 5f) =% .5f’ % (muestra[[best_ix], sample_eval[[best_ix])) |
La ejecución del ejemplo genera una muestra aleatoria de valores de entrada, que luego se evalúan. A continuación, se identifica y se informa el punto de mejor rendimiento.
Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o procedimiento de evaluación, o las diferencias en la precisión numérica. Considere ejecutar el ejemplo varias veces y compare el resultado promedio.
En este caso, podemos ver que el resultado está muy cerca de la entrada óptima de 0.0.
|
Mejor: f (-0.01762) = 0.00031 |
Podemos actualizar el ejemplo para trazar la función objetivo y mostrar la muestra y el mejor resultado. El ejemplo completo se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
# ejemplo de búsqueda aleatoria para optimización de funciones con gráfico desde numpy importar arange desde numpy.aleatorio importar rand desde matplotlib importar pyplot # función objetiva def objetivo(X): regreso X**2.0 # definir rango para entrada r_min, r_max = –5,0, 5,0 # generar una muestra aleatoria del dominio muestra = r_min + rand(100) * (r_max – r_min) # evaluar la muestra sample_eval = objetivo(muestra) # localizar la mejor solución best_ix = 0 por I en abarcar(len(muestra)): si sample_eval[[I] < sample_eval[[best_ix]: best_ix = I # resumir la mejor solución imprimir(‘Mejor: f (%. 5f) =% .5f’ % (muestra[[best_ix], sample_eval[[best_ix])) # rango de entrada de muestra uniformemente en incrementos de 0.1 entradas = arange(r_min, r_max, 0,1) # calcular objetivos resultados = objetivo(entradas) # crear una gráfica de línea de entrada vs resultado pyplot.trama(entradas, resultados) # trazar la muestra pyplot.dispersión(muestra, sample_eval) # dibuja una línea vertical en la mejor entrada pyplot.axvline(X=muestra[[best_ix], ls=‘-‘, color=‘rojo’) # mostrar la trama pyplot.show() |
Ejecutar el ejemplo nuevamente genera la muestra aleatoria y reporta el mejor resultado.
|
Mejor: f (0.01934) = 0.00037 |
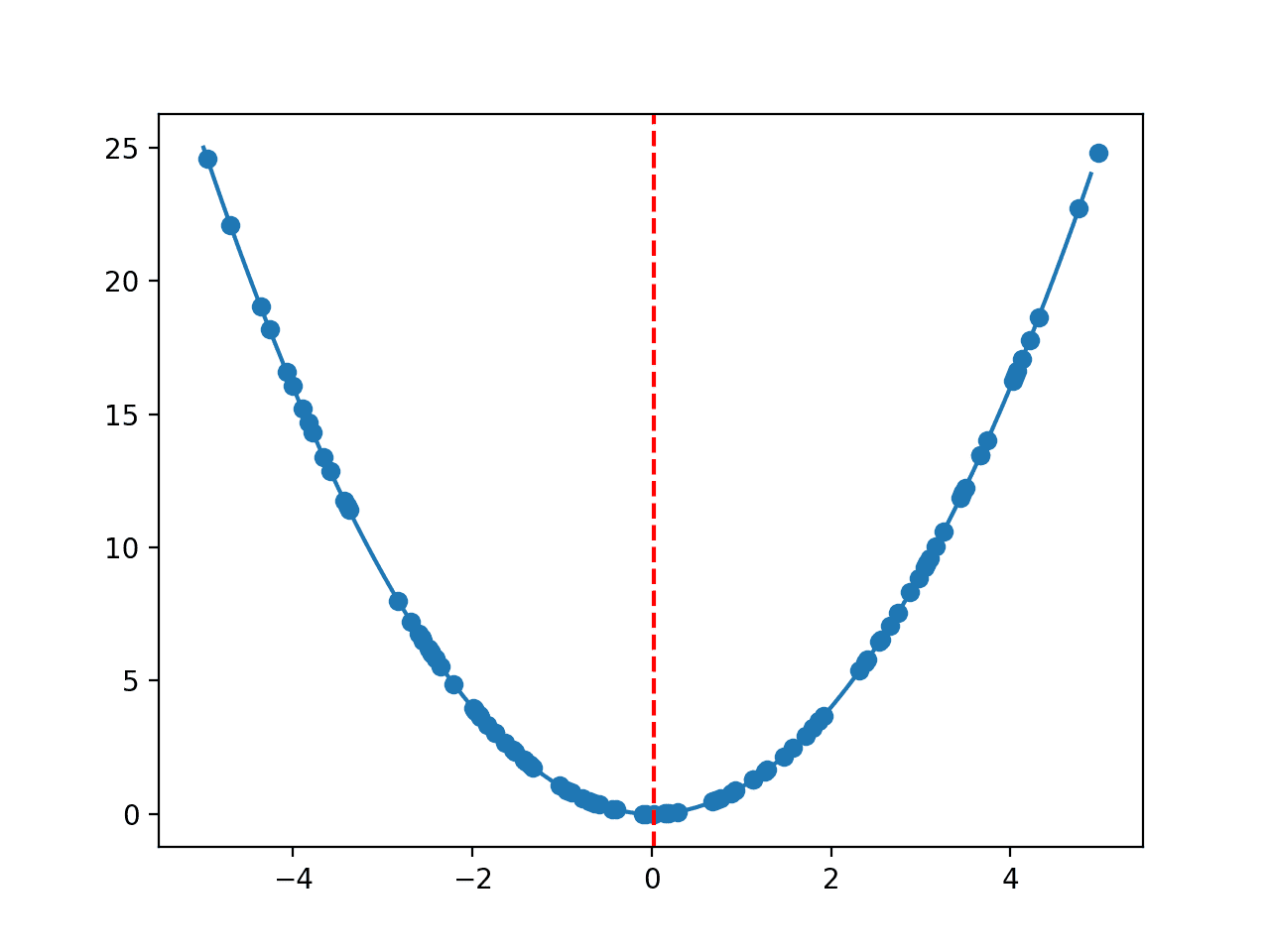
Luego, se crea un gráfico de líneas que muestra la forma de la función objetivo, la muestra aleatoria y una línea roja para obtener el mejor resultado ubicado en la muestra.

Gráfico de línea de la función objetivo unidimensional con muestra aleatoria
Búsqueda de cuadrícula para optimización de funciones
La búsqueda de cuadrícula también se conoce como muestreo de cuadrícula o muestreo factorial completo.
La búsqueda de cuadrícula implica generar entradas de cuadrícula uniformes para una función objetivo. En una dimensión, estas serían entradas espaciadas uniformemente a lo largo de una línea. En dos dimensiones, esto sería una celosía de puntos espaciados uniformemente a través de la superficie, y así sucesivamente para dimensiones más altas.
El plan de muestreo factorial completo coloca una cuadrícula de puntos espaciados uniformemente sobre el espacio de búsqueda. Este enfoque es fácil de implementar, no se basa en la aleatoriedad y cubre el espacio, pero utiliza una gran cantidad de puntos.
– Página 235, Algoritmos de optimización, 2019.
Al igual que la búsqueda aleatoria, una búsqueda en cuadrícula puede ser particularmente eficaz en problemas en los que la experiencia en el dominio se utiliza normalmente para influir en la selección de algoritmos de optimización específicos. La cuadrícula puede ayudar a identificar rápidamente áreas de un espacio de búsqueda que pueden merecer más atención.
La cuadrícula de muestras suele ser uniforme, aunque no tiene por qué ser así. Por ejemplo, se podría utilizar una escala log-10 con un espaciado uniforme, lo que permitiría realizar el muestreo en distintos órdenes de magnitud.
La desventaja es que la aspereza de la cuadrícula puede atravesar regiones enteras del espacio de búsqueda donde residen buenas soluciones, un problema que empeora a medida que aumenta el número de entradas (dimensiones del espacio de búsqueda) al problema.
Se puede generar una cuadrícula de muestras eligiendo la separación uniforme de puntos, luego enumerando cada variable por turno e incrementando cada variable por la separación elegida.
El siguiente ejemplo da un ejemplo de una función de objetivo de minimización bidimensional simple y genera y luego evalúa una muestra de cuadrícula con un espaciado de 0.1 para ambas variables de entrada. A continuación, se informa la entrada con el mejor rendimiento.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 |
# ejemplo de búsqueda de cuadrícula para optimización de funciones desde numpy importar arange desde numpy.aleatorio importar rand # función objetiva def objetivo(X, y): regreso X**2.0 + y **2.0 # definir rango para entrada r_min, r_max = –5,0, 5,0 # generar una muestra de cuadrícula del dominio muestra = lista() paso = 0,1 por X en arange(r_min, r_max+paso, paso): por y en arange(r_min, r_max+paso, paso): muestra.adjuntar([[X,y]) # evaluar la muestra sample_eval = [[objetivo(X,y) por X,y en muestra] # localizar la mejor solución best_ix = 0 por I en abarcar(len(muestra)): si sample_eval[[I] < sample_eval[[best_ix]: best_ix = I # resumir la mejor solución imprimir(‘Mejor: f (%. 5f,%. 5f) =% .5f’ % (muestra[[best_ix][[0], muestra[[best_ix][[1], sample_eval[[best_ix])) |
La ejecución del ejemplo genera una cuadrícula de valores de entrada, que luego se evalúan. A continuación, se identifica y se informa el punto de mejor rendimiento.
Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o procedimiento de evaluación, o las diferencias en la precisión numérica. Considere ejecutar el ejemplo varias veces y compare el resultado promedio.
En este caso, podemos ver que el resultado encuentra el óptimo exactamente.
|
Mejor: f (-0,00000, -0,00000) = 0,00000 |
Podemos actualizar el ejemplo para trazar la función objetivo y mostrar la muestra y el mejor resultado. El ejemplo completo se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
# ejemplo de búsqueda de cuadrícula para optimización de funciones con gráfico desde numpy importar arange desde numpy importar rejilla desde numpy.aleatorio importar rand desde matplotlib importar pyplot # función objetiva def objetivo(X, y): regreso X**2.0 + y **2.0 # definir rango para entrada r_min, r_max = –5,0, 5,0 # generar una muestra de cuadrícula del dominio muestra = lista() paso = 0,5 por X en arange(r_min, r_max+paso, paso): por y en arange(r_min, r_max+paso, paso): muestra.adjuntar([[X,y]) # evaluar la muestra sample_eval = [[objetivo(X,y) por X,y en muestra] # localizar la mejor solución best_ix = 0 por I en abarcar(len(muestra)): si sample_eval[[I] < sample_eval[[best_ix]: best_ix = I # resumir la mejor solución imprimir(‘Mejor: f (%. 5f,%. 5f) =% .5f’ % (muestra[[best_ix][[0], muestra[[best_ix][[1], sample_eval[[best_ix])) # rango de entrada de muestra uniformemente en incrementos de 0.1 xaxis = arange(r_min, r_max, 0,1) yaxis = arange(r_min, r_max, 0,1) # crea una malla a partir del eje X, y = rejilla(xaxis, yaxis) # calcular objetivos resultados = objetivo(X, y) # crear un gráfico de contorno relleno pyplot.contourf(X, y, resultados, niveles=50, cmap=‘chorro’) # trazar la muestra como círculos negros pyplot.trama([[X por X,_ en muestra], [[y por _,y en muestra], ‘.’, color=‘negro’) # dibuja el mejor resultado como una estrella blanca pyplot.trama(muestra[[best_ix][[0], muestra[[best_ix][[1], ‘*’, color=‘blanco’) # mostrar la trama pyplot.show() |
Ejecutar el ejemplo nuevamente genera la muestra de cuadrícula y reporta el mejor resultado.
|
Mejor: f (0.00000,0.00000) = 0.00000 |
Luego, se crea un gráfico de contorno que muestra la forma de la función objetivo, la muestra de la cuadrícula como puntos negros y una estrella blanca para obtener el mejor resultado ubicado en la muestra.
Tenga en cuenta que algunos de los puntos negros del borde del dominio parecen estar fuera de la trama; esto es solo un artefacto de cómo elegimos dibujar los puntos (por ejemplo, no centrados en la muestra).
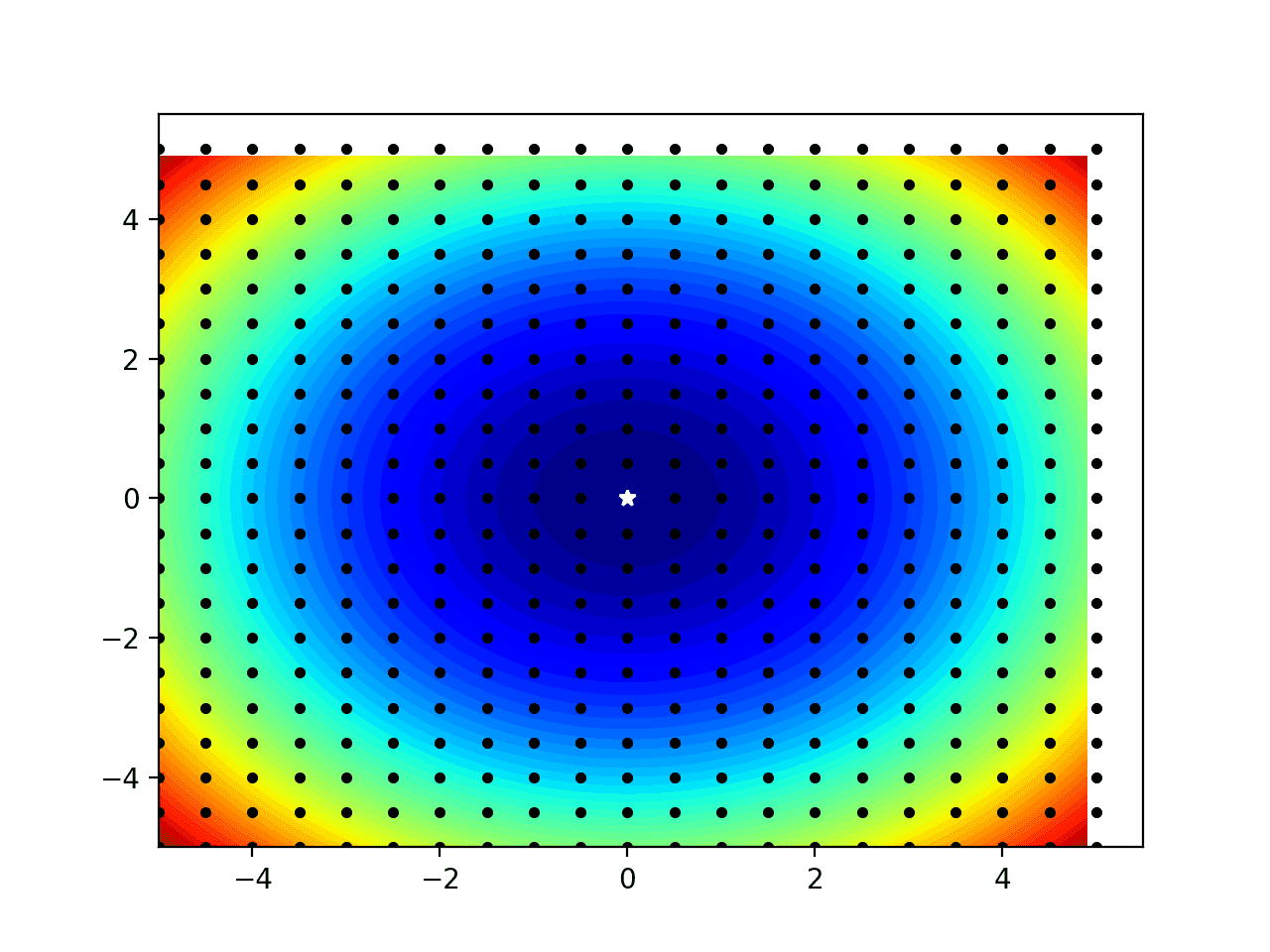
Gráfico de contorno de la función objetiva unidimensional con muestra de cuadrícula
Otras lecturas
Esta sección proporciona más recursos sobre el tema si desea profundizar.
Libros
Artículos
Resumen
En este tutorial, descubrió algoritmos ingenuos para la optimización de funciones.
Específicamente, aprendiste:
- El papel de los algoritmos ingenuos en los proyectos de optimización de funciones.
- Cómo generar y evaluar una búsqueda aleatoria para la optimización de funciones.
- Cómo generar y evaluar una búsqueda de cuadrícula para la optimización de funciones.
¿Tiene usted alguna pregunta?
Haga sus preguntas en los comentarios a continuación y haré todo lo posible para responder.
