Optimización de funciones implica encontrar la entrada que resulte en el valor óptimo de una función objetivo.
Los algoritmos de optimización navegan por el espacio de búsqueda de las variables de entrada para localizar los óptimos, y tanto la forma de la función objetivo como el comportamiento del algoritmo en el espacio de búsqueda son opacos en los problemas del mundo real.
Como tal, es común estudiar algoritmos de optimización utilizando funciones simples de baja dimensión que se pueden visualizar fácilmente directamente. Además, las muestras en el espacio de entrada de estas funciones simples realizadas por un algoritmo de optimización se pueden visualizar con su contexto apropiado.
La visualización de funciones de dimensiones inferiores y el comportamiento del algoritmo en esas funciones pueden ayudar a desarrollar las intuiciones que pueden traspasar a problemas de optimización de funciones de dimensiones superiores más complejos más adelante.
En este tutorial, descubrirá cómo crear visualizaciones para la optimización de funciones en Python.
Después de completar este tutorial, sabrá:
- La visualización es una herramienta importante al estudiar los algoritmos de optimización de funciones.
- Cómo visualizar muestras y funciones unidimensionales mediante diagramas de líneas.
- Cómo visualizar muestras y funciones bidimensionales mediante diagramas de contorno y superficie.
Empecemos.

Visualización para la optimización de funciones en Python
Foto de Nathalie, algunos derechos reservados.
Descripción general del tutorial
Este tutorial se divide en tres partes; son:
- Visualización para optimización de funciones
- Visualice la optimización de funciones 1D
- Función de prueba
- Función de prueba de muestra
- Gráfico de línea de la función de prueba
- Gráfico de dispersión de la función de prueba
- Gráfico de línea con Optima marcado
- Gráfico de línea con muestras
- Visualice la optimización de funciones 2D
- Función de prueba
- Función de prueba de muestra
- Gráfico de contorno de la función de prueba
- Gráfico de contorno relleno de la función de prueba
- Gráfico de contorno relleno de la función de prueba con muestras
- Gráfico de superficie de la función de prueba
Visualización para optimización de funciones
La optimización de funciones es un campo de las matemáticas que se ocupa de encontrar las entradas a una función que dan como resultado la salida óptima para la función, generalmente un valor mínimo o máximo.
La optimización puede ser sencilla para funciones diferenciales simples donde la solución se puede calcular analíticamente. Sin embargo, la mayoría de las funciones que estamos interesados en resolver en el aprendizaje automático aplicado pueden o no comportarse bien y pueden ser complejas, no lineales, multivariadas y no diferenciables.
Como tal, es importante comprender una amplia gama de algoritmos diferentes que se pueden utilizar para abordar problemas de optimización de funciones.
Un aspecto importante del estudio de la optimización de funciones es comprender la función objetivo que se está optimizando y comprender el comportamiento de un algoritmo de optimización a lo largo del tiempo.
La visualización juega un papel importante al comenzar con la optimización de funciones.
Podemos seleccionar funciones de prueba simples y bien entendidas para estudiar algoritmos de optimización. Estas funciones simples se pueden trazar para comprender la relación entre la entrada a la función objetivo y la salida de la función objetivo y resaltar colinas, valles y óptimos.
Además, las muestras seleccionadas del espacio de búsqueda mediante un algoritmo de optimización también se pueden representar en la parte superior de los gráficos de la función objetivo. Estos gráficos de comportamiento de algoritmos pueden proporcionar información e intuición sobre cómo funcionan los algoritmos de optimización específicos y navegar por un espacio de búsqueda que puede generalizarse a nuevos problemas en el futuro.
Por lo general, las funciones unidimensionales o bidimensionales se eligen para estudiar los algoritmos de optimización, ya que son fáciles de visualizar utilizando gráficos estándar, como gráficos de líneas y gráficos de superficie. Exploraremos ambos en este tutorial.
Primero, exploremos cómo podríamos visualizar una optimización de función unidimensional.
Visualice la optimización de funciones 1D
Una función unidimensional toma una sola variable de entrada y genera la evaluación de esa variable de entrada.
Las variables de entrada son típicamente continuas, representadas por un valor de punto flotante de valor real. A menudo, el dominio de entrada no está restringido, aunque para los problemas de prueba imponemos un dominio de interés.
Función de prueba
En este caso, exploraremos la visualización de funciones con una función objetivo simple x ^ 2:
Esto tiene un valor óptimo con una entrada de x = 0.0, que es igual a 0.0.
El siguiente ejemplo implementa esta función objetivo y evalúa una única entrada.
|
# ejemplo de función objetivo 1d # función objetiva def objetivo(X): regreso X**2.0 # evaluar las entradas a la función objetivo X = 4.0 resultado = objetivo(X) impresión(‘f (%. 3f) =% .3f’ % (X, resultado)) |
Ejecutar el ejemplo evalúa el valor 4.0 con la función objetivo, que es igual a 16.0.
Pruebe la función de prueba
Lo primero que podríamos querer hacer con una nueva función es definir un rango de entrada de interés y muestrear el dominio de interés usando una cuadrícula uniforme.
Esta muestra proporcionará la base para generar un gráfico más adelante.
En este caso, definiremos un dominio de interés alrededor de los óptimos de x = 0.0 desde x = -5.0 ax = 5.0 y muestrearemos una cuadrícula de valores en este rango con incrementos de 0.1, tales como -5.0, -4.9, -4.8 etc.
|
... # definir rango para entrada r_min, r_max = –5,0, 5,0 # rango de entrada de muestra uniformemente en incrementos de 0.1 entradas = arange(r_min, r_max, 0,1) # resumir algunos de los dominios de entrada impresión(entradas[[:5]) |
Entonces podemos evaluar cada uno de los valores de x en nuestra muestra.
|
... # calcular objetivos resultados = objetivo(entradas) # resumir algunos de los resultados impresión(resultados[[:5]) |
Finalmente, podemos verificar algunas de las entradas y sus correspondientes salidas.
|
... # crear un mapeo de algunas entradas a algunos resultados para yo en rango(5): impresión(‘f (%. 3f) =% .3f’ % (entradas[[yo], resultados[[yo])) |
Al unir esto, el ejemplo completo de muestreo del espacio de entrada y evaluación de todos los puntos de la muestra se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 |
# función objetivo 1d de muestra desde numpy importar arange # función objetiva def objetivo(X): regreso X**2.0 # definir rango para entrada r_min, r_max = –5,0, 5,0 # rango de entrada de muestra uniformemente en incrementos de 0.1 entradas = arange(r_min, r_max, 0,1) # resumir algunos de los dominios de entrada impresión(entradas[[:5]) # calcular objetivos resultados = objetivo(entradas) # resumir algunos de los resultados impresión(resultados[[:5]) # crear un mapeo de algunas entradas a algunos resultados para yo en rango(5): impresión(‘f (%. 3f) =% .3f’ % (entradas[[yo], resultados[[yo])) |
Ejecutar el ejemplo primero genera una muestra uniforme de puntos de entrada como esperábamos.
Luego, los puntos de entrada se evalúan utilizando la función objetivo y, finalmente, podemos ver un mapeo simple de entradas y salidas de la función objetivo.
|
[-5. -4.9 -4.8 -4.7 -4.6]
[25. 24.01 23.04 22.09 21.16]
f (-5.000) = 25.000 f (-4,900) = 24,010 f (-4.800) = 23.040 f (-4.700) = 22.090 f (-4.600) = 21.160 |
Ahora que tenemos cierta confianza en generar una muestra de entradas y evaluarlas con la función objetivo, podemos buscar generar gráficos de la función.
Gráfico de línea de la función de prueba
Podríamos muestrear el espacio de entrada al azar, pero el beneficio de una línea o cuadrícula de puntos uniforme es que se puede usar para generar una gráfica suave.
Es suave porque los puntos en el espacio de entrada están ordenados de menor a mayor. Este orden es importante ya que esperamos (esperamos) que la salida de la función objetivo tenga una relación suave similar entre los valores, p. pequeños cambios en la entrada dan como resultado cambios localmente consistentes (suaves) en la salida de la función.
En este caso, podemos usar las muestras para generar una gráfica lineal de la función objetivo con los puntos de entrada (x) en el eje x de la gráfica y la salida (resultados) de la función objetivo en el eje y de la gráfica.
|
... # crear una gráfica de línea de entrada vs resultado pyplot.trama(entradas, resultados) # mostrar la trama pyplot.show() |
Al unir esto, el ejemplo completo se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 |
# gráfica de línea de entrada vs resultado para una función objetivo 1d desde numpy importar arange desde matplotlib importar pyplot # función objetiva def objetivo(X): regreso X**2.0 # definir rango para entrada r_min, r_max = –5,0, 5,0 # rango de entrada de muestra uniformemente en incrementos de 0.1 entradas = arange(r_min, r_max, 0,1) # calcular objetivos resultados = objetivo(entradas) # crear una gráfica de línea de entrada vs resultado pyplot.trama(entradas, resultados) # mostrar la trama pyplot.show() |
La ejecución del ejemplo crea un gráfico de líneas de la función objetivo.
Podemos ver que la función tiene una forma de U grande, llamada parábola. Esta es una forma común al estudiar curvas, p. Ej. el estudio del cálculo.
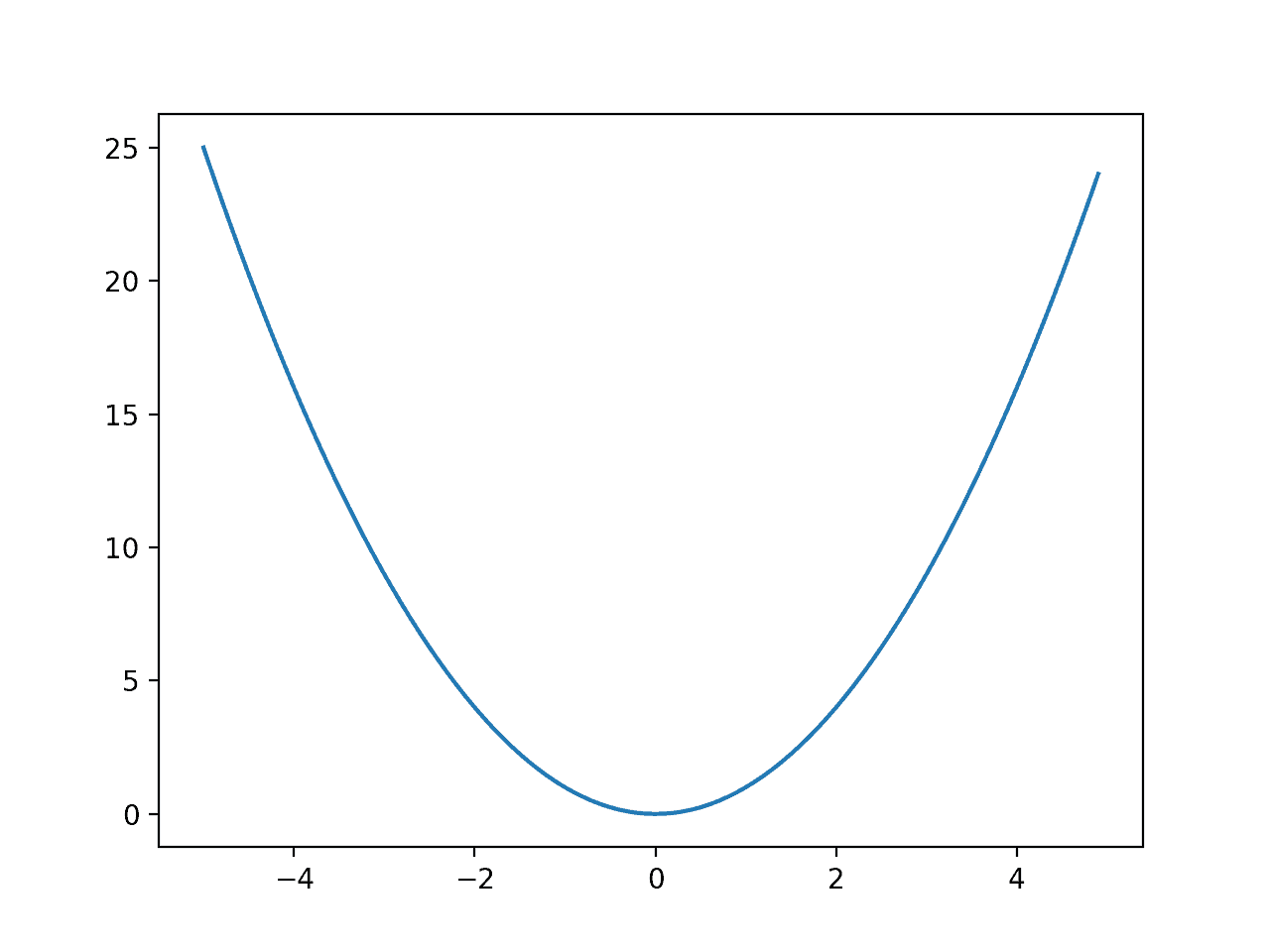
Gráfico de línea de una función unidimensional
Gráfico de dispersión de la función de prueba
La línea es una construcción. No es realmente la función, solo un resumen suave de la función. Siempre tenga esto en cuenta.
Recuerde que, de hecho, generamos una muestra de puntos en el espacio de entrada y la evaluación correspondiente de esos puntos.
Como tal, sería más preciso crear un diagrama de dispersión de puntos; por ejemplo:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 |
# gráfico de dispersión de entrada vs resultado para una función objetivo 1d desde numpy importar arange desde matplotlib importar pyplot # función objetiva def objetivo(X): regreso X**2.0 # definir rango para entrada r_min, r_max = –5,0, 5,0 # rango de entrada de muestra uniformemente en incrementos de 0.1 entradas = arange(r_min, r_max, 0,1) # calcular objetivos resultados = objetivo(entradas) # crear un diagrama de dispersión de entrada vs resultado pyplot.dispersión(entradas, resultados) # mostrar la trama pyplot.show() |
La ejecución del ejemplo crea un diagrama de dispersión de la función objetivo.
Podemos ver la forma familiar de la función, pero no ganamos nada al trazar los puntos directamente.
La línea y la interpolación suave entre los puntos que proporciona son más útiles, ya que podemos dibujar otros puntos en la parte superior de la línea, como la ubicación de los óptimos o los puntos muestreados por un algoritmo de optimización.
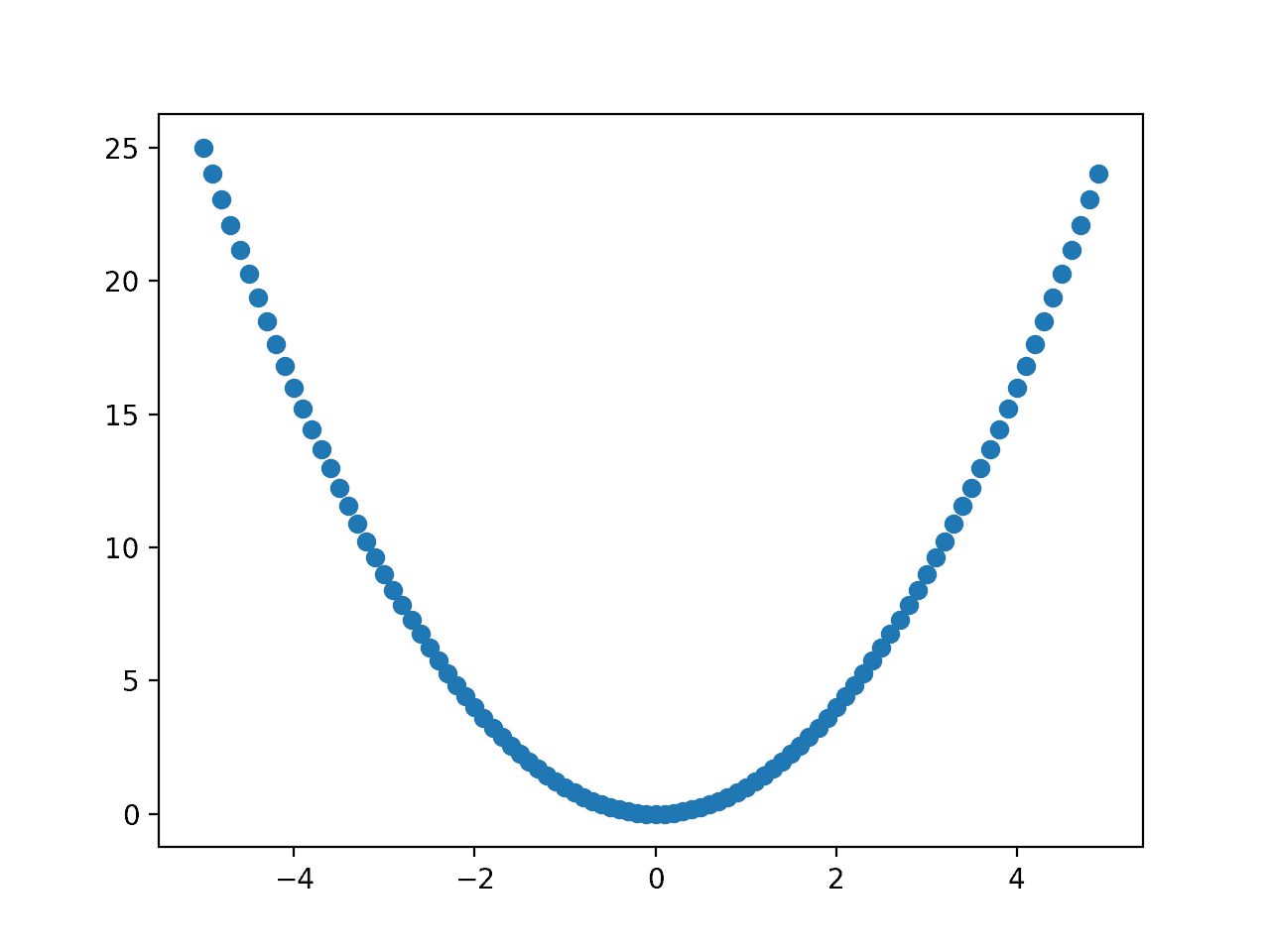
Diagrama de dispersión de una función unidimensional
Gráfico de línea con Optima marcado
A continuación, dibujemos de nuevo la gráfica lineal y esta vez dibujemos un punto donde se ubica el óptimo conocido de la función.
Esto puede ser útil al estudiar un algoritmo de optimización, ya que es posible que deseemos ver qué tan cerca puede llegar un algoritmo de optimización al óptimo.
Primero, debemos definir la entrada para los óptimos, luego evaluar ese punto para obtener los valores del eje xy del eje y para el trazado.
|
... # definir la función conocida optima optima_x = 0.0 optima_y = objetivo(optima_x) |
Luego podemos trazar este punto con cualquier forma o color que nos guste, en este caso, un cuadrado rojo.
|
... # dibuja la función optima como un cuadrado rojo pyplot.trama([[optima_x], [[optima_y], ‘s’, color=‘r’) |
Al unir esto, el ejemplo completo de creación de un diagrama de línea de la función con los óptimos resaltados por un punto se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 |
# gráfico de línea de entrada vs resultado para una función objetivo 1d y mostrar óptimos desde numpy importar arange desde matplotlib importar pyplot # función objetiva def objetivo(X): regreso X**2.0 # definir rango para entrada r_min, r_max = –5,0, 5,0 # rango de entrada de muestra uniformemente en incrementos de 0.1 entradas = arange(r_min, r_max, 0,1) # calcular objetivos resultados = objetivo(entradas) # crear una gráfica de línea de entrada vs resultado pyplot.trama(entradas, resultados) # definir la función conocida optima optima_x = 0.0 optima_y = objetivo(optima_x) # dibuja la función optima como un cuadrado rojo pyplot.trama([[optima_x], [[optima_y], ‘s’, color=‘r’) # mostrar la trama pyplot.show() |
Ejecutar el ejemplo crea el gráfico de línea familiar de la función, y esta vez, el óptimo de la función, p. Ej. la entrada que da como resultado la salida mínima de la función, está marcada con un cuadrado rojo.
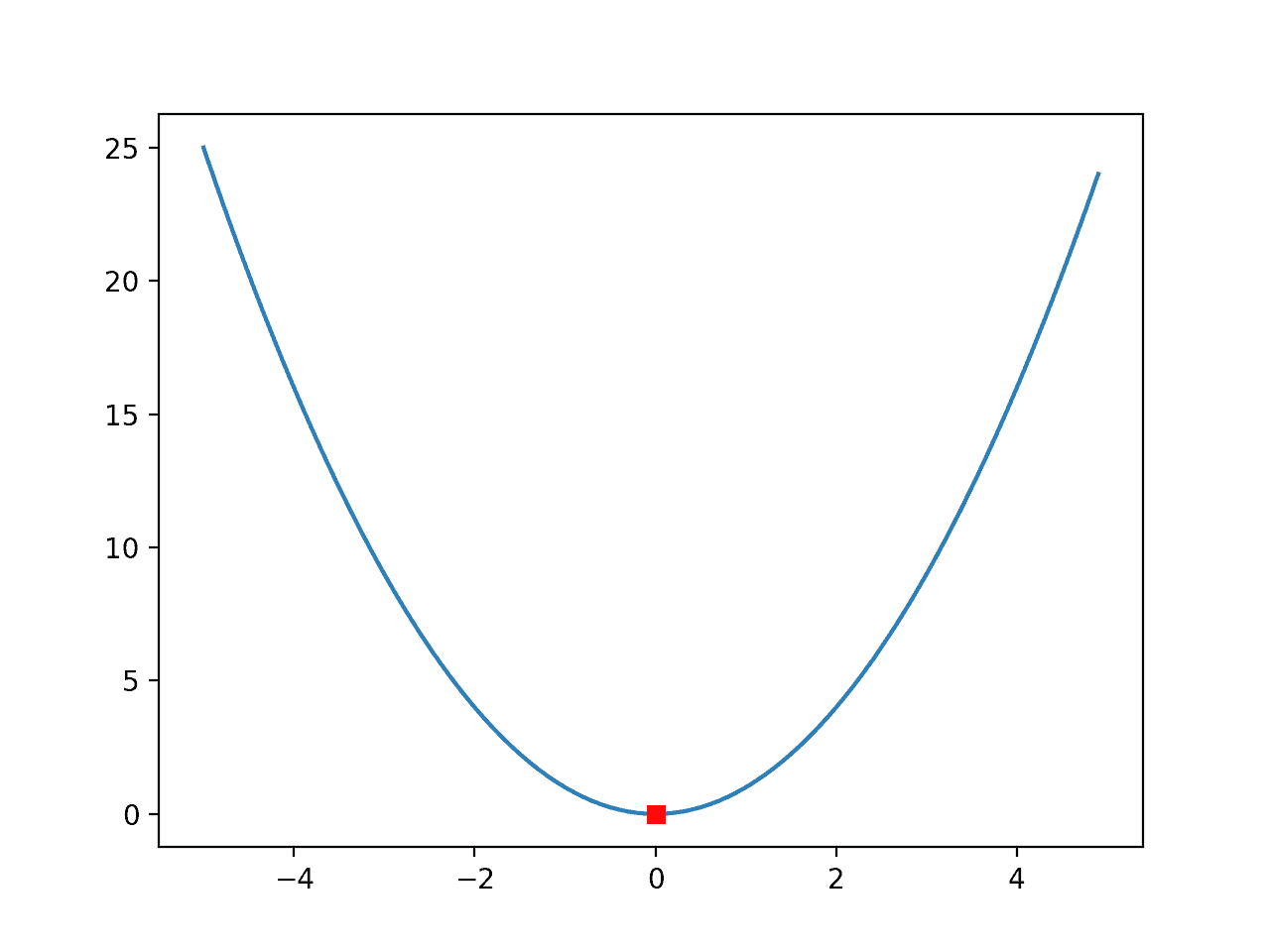
Gráfico de línea de una función unidimensional con Optima marcado por un cuadrado rojo
Esta es una función muy simple y el cuadrado rojo del optima es fácil de ver.
A veces, la función puede ser más compleja, con muchas colinas y valles, y es posible que queramos hacer que los óptimos sean más visibles.
En este caso, podemos dibujar una línea vertical a lo largo de toda la parcela.
|
... # dibuja una línea vertical en la entrada óptima pyplot.axvline(X=optima_x, ls=‘-‘, color=‘rojo’) |
Al unir esto, el ejemplo completo se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 |
# gráfico de línea de entrada vs resultado para una función objetivo 1d y muestra óptimos como línea desde numpy importar arange desde matplotlib importar pyplot # función objetiva def objetivo(X): regreso X**2.0 # definir rango para entrada r_min, r_max = –5,0, 5,0 # rango de entrada de muestra uniformemente en incrementos de 0.1 entradas = arange(r_min, r_max, 0,1) # calcular objetivos resultados = objetivo(entradas) # crear una gráfica de línea de entrada vs resultado pyplot.trama(entradas, resultados) # definir la función conocida optima optima_x = 0.0 # dibuja una línea vertical en la entrada óptima pyplot.axvline(X=optima_x, ls=‘-‘, color=‘rojo’) # mostrar la trama pyplot.show() |
Al ejecutar el ejemplo, se crea el mismo gráfico y esta vez se dibuja una línea roja que marca claramente el punto en el espacio de entrada que marca los óptimos.
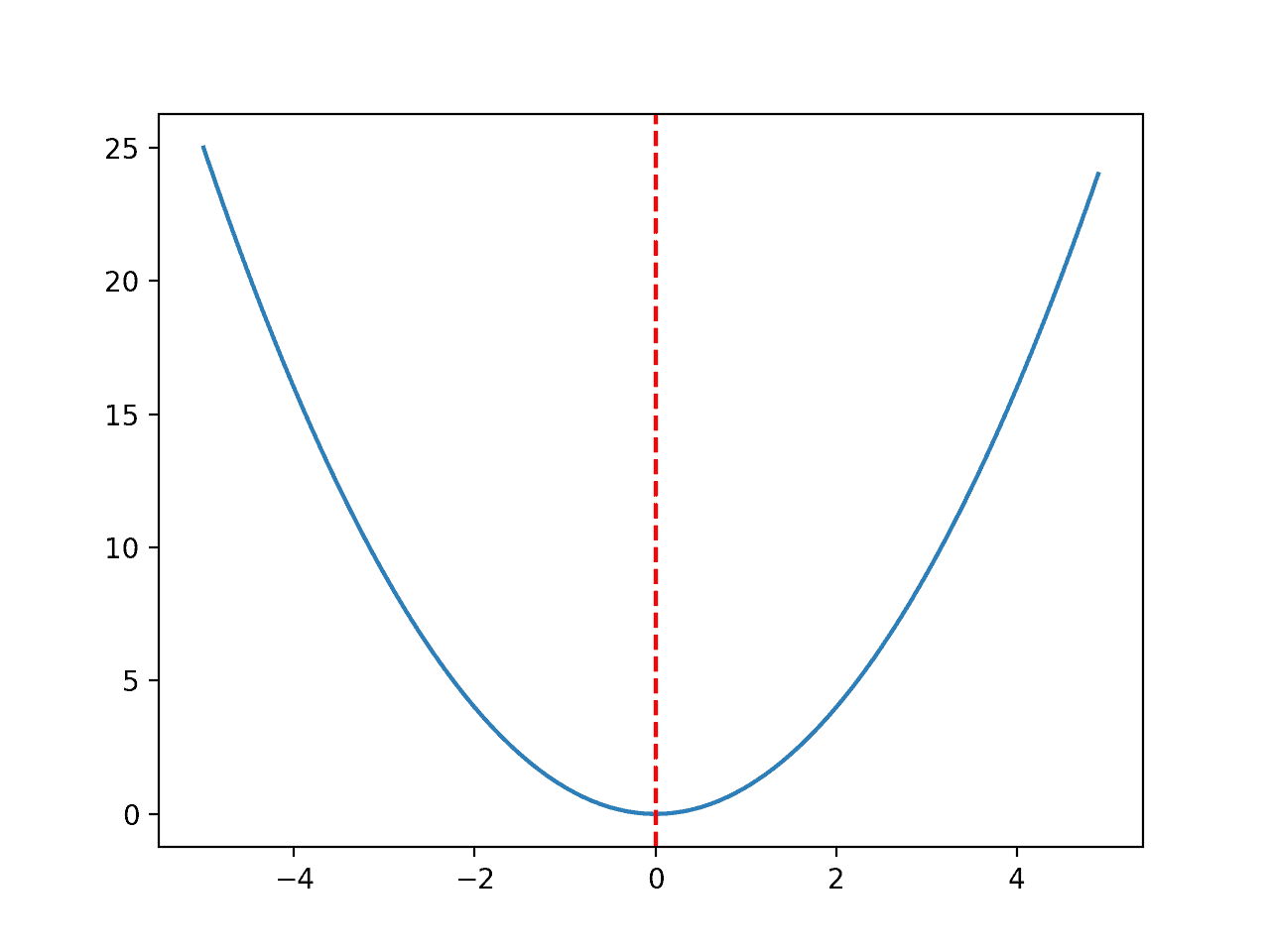
Gráfico de línea de una función unidimensional con Optima marcado por una línea roja
Gráfico de línea con muestras
Finalmente, es posible que deseemos extraer las muestras del espacio de entrada seleccionado por un algoritmo de optimización.
Simularemos estas muestras con puntos aleatorios extraídos del dominio de entrada.
|
... # simular una muestra hecha por un algoritmo de optimización semilla(1) muestra = r_min + rand(10) * (r_max – r_min) # evaluar la muestra sample_eval = objetivo(muestra) |
Luego podemos graficar esta muestra, en este caso usando pequeños círculos negros.
|
... # trazar la muestra como círculos negros pyplot.trama(muestra, sample_eval, ‘o’, color=‘negro’) |
El ejemplo completo de creación de un diagrama de línea de una función con los óptimos marcados con una línea roja y una muestra de algoritmo dibujada con pequeños puntos negros se muestra a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
# gráfica de línea de dominio para una función 1d con muestra de algoritmo y optima desde numpy importar arange desde numpy.aleatorio importar semilla desde numpy.aleatorio importar rand desde matplotlib importar pyplot # función objetiva def objetivo(X): regreso X**2.0 # definir rango para entrada r_min, r_max = –5,0, 5,0 # rango de entrada de muestra uniformemente en incrementos de 0.1 entradas = arange(r_min, r_max, 0,1) # calcular objetivos resultados = objetivo(entradas) # simular una muestra hecha por un algoritmo de optimización semilla(1) muestra = r_min + rand(10) * (r_max – r_min) # evaluar la muestra sample_eval = objetivo(muestra) # crear una gráfica de línea de entrada vs resultado pyplot.trama(entradas, resultados) # definir la función conocida optima optima_x = 0.0 # dibuja una línea vertical en la entrada óptima pyplot.axvline(X=optima_x, ls=‘-‘, color=‘rojo’) # trazar la muestra como círculos negros pyplot.trama(muestra, sample_eval, ‘o’, color=‘negro’) # mostrar la trama pyplot.show() |
Al ejecutar el ejemplo, se crea el gráfico de línea del dominio y se marca el óptimo con una línea roja como antes.
Esta vez, la muestra del dominio seleccionado por un algoritmo (en realidad una muestra aleatoria de puntos) se dibuja con puntos negros.
Podemos imaginar que un algoritmo de optimización real mostrará puntos que se estrechan en el dominio mientras busca cuesta abajo desde un punto de partida.
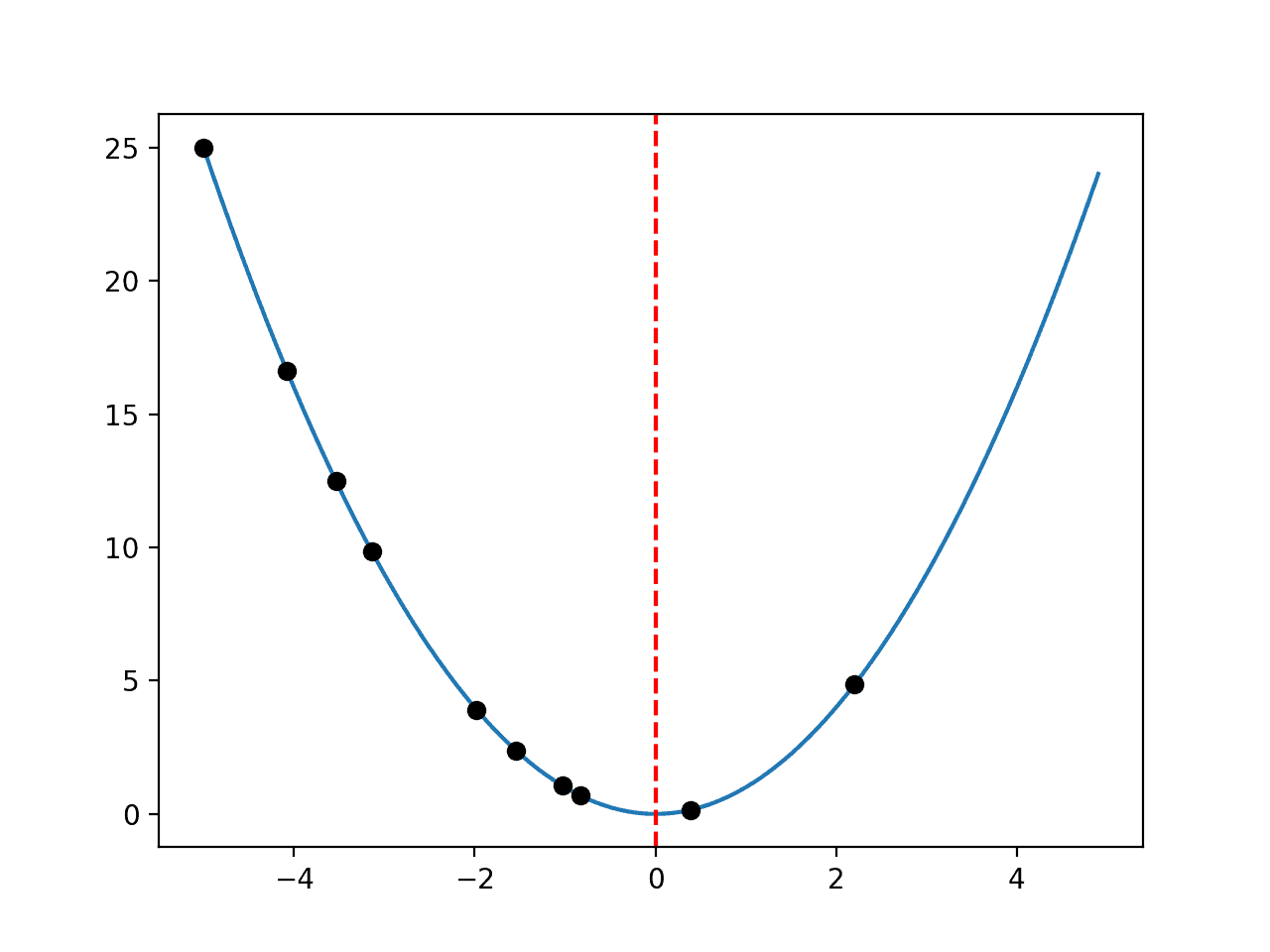
Gráfico de línea de una función unidimensional con Optima marcado por una línea roja y muestras mostradas con puntos negros
A continuación, veamos cómo podríamos realizar visualizaciones similares para la optimización de una función bidimensional.
Visualice la optimización de funciones 2D
Una función bidimensional es una función que toma dos variables de entrada, p. Ej. X y y.
Función de prueba
Podemos usar lo mismo x ^ 2 funcionar y escalarlo para que sea una función bidimensional; por ejemplo:
Esto tiene un valor óptimo con una entrada de [x=0.0, y=0.0], que es igual a 0.0.
El siguiente ejemplo implementa esta función objetivo y evalúa una única entrada.
|
# ejemplo de función objetivo 2d # función objetiva def objetivo(X, y): regreso X**2.0 + y **2.0 # evaluar las entradas a la función objetivo X = 4.0 y = 4.0 resultado = objetivo(X, y) impresión(‘f (%. 3f,% .3f) =% .3f’ % (X, y, resultado)) |
Ejecutar el ejemplo evalúa el punto [x=4, y=4], que es igual a 32.
A continuación, necesitamos una forma de muestrear el dominio para que podamos, a su vez, muestrear la función objetivo.
Función de prueba de muestra
Una forma común de muestrear una función bidimensional es generar primero una muestra uniforme a lo largo de cada variable, X y y, luego use estas dos muestras uniformes para crear una cuadrícula de muestras, llamada cuadrícula de malla.
Esta no es una matriz bidimensional en el espacio de entrada; en cambio, son dos matrices bidimensionales que, cuando se usan juntas, definen una cuadrícula entre las dos variables de entrada.
Esto se logra duplicando todo el X matriz de muestra para cada y punto de muestra y de manera similar duplicando todo el y matriz de muestra para cada X punto de muestreo.
Esto se puede lograr usando la función meshgrid () NumPy; por ejemplo:
|
... # definir rango para entrada r_min, r_max = –5,0, 5,0 # rango de entrada de muestra uniformemente en incrementos de 0.1 xaxis = arange(r_min, r_max, 0,1) yaxis = arange(r_min, r_max, 0,1) # create a mesh from the axis X, y = meshgrid(xaxis, yaxis) # summarize some of the input domain print(X[[:5, :5]) |
We can then evaluate each pair of points using our objective function.
|
... # compute targets resultados = objetivo(X, y) # summarize some of the results print(resultados[[:5, :5]) |
Finally, we can review the mapping of some of the inputs to their corresponding output values.
|
... # create a mapping of some inputs to some results para i en rango(5): print(‘f(%.3f, %.3f) = %.3f’ % (X[[i,0], y[[i,0], resultados[[i,0])) |
The example below demonstrates how we can create a uniform sample grid across the two-dimensional input space and objective function.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 |
# sample 2d objective function desde numpy import arange desde numpy import meshgrid # objective function def objetivo(X, y): regreso x**2.0 + y**2.0 # define range for input r_min, r_max = –5.0, 5.0 # sample input range uniformly at 0.1 increments xaxis = arange(r_min, r_max, 0.1) yaxis = arange(r_min, r_max, 0.1) # create a mesh from the axis X, y = meshgrid(xaxis, yaxis) # summarize some of the input domain print(X[[:5, :5]) # compute targets resultados = objetivo(X, y) # summarize some of the results print(resultados[[:5, :5]) # create a mapping of some inputs to some results para i en rango(5): print(‘f(%.3f, %.3f) = %.3f’ % (X[[i,0], y[[i,0], resultados[[i,0])) |
Running the example first summarizes some points in the mesh grid, then the objective function evaluation for some points.
Finally, we enumerate coordinates in the two-dimensional input space and their corresponding function evaluation.
|
[[[-5. -4.9 -4.8 -4.7 -4.6]
[-5. -4.9 -4.8 -4.7 -4.6] [-5. -4.9 -4.8 -4.7 -4.6] [-5. -4.9 -4.8 -4.7 -4.6] [-5. -4.9 -4.8 -4.7 -4.6]] [[50. 49.01 48.04 47.09 46.16] [49.01 48.02 47.05 46.1 45.17] [48.04 47.05 46.08 45.13 44.2 ] [47.09 46.1 45.13 44.18 43.25] [46.16 45.17 44.2 43.25 42.32]] f(-5.000, -5.000) = 50.000 f(-5.000, -4.900) = 49.010 f(-5.000, -4.800) = 48.040 f(-5.000, -4.700) = 47.090 f(-5.000, -4.600) = 46.160 |
Now that we are familiar with how to sample the input space and evaluate points, let’s look at how we might plot the function.
Contour Plot of Test Function
A popular plot for two-dimensional functions is a contour plot.
This plot creates a flat representation of the objective function outputs for each x and y coordinate where the color and contour lines indicate the relative value or height of the output of the objective function.
This is just like a contour map of a landscape where mountains can be distinguished from valleys.
This can be achieved using the contour() Matplotlib function that takes the mesh grid and the evaluation of the mesh grid as input directly.
We can then specify the number of levels to draw on the contour and the color scheme to use. In this case, we will use 50 levels and a popular “jet” color scheme where low-levels use a cold color scheme (blue) and high-levels use a hot color scheme (red).
|
... # create a contour plot with 50 levels and jet color scheme pyplot.contour(X, y, resultados, 50, alpha=1.0, cmap=‘jet’) # show the plot pyplot.show() |
Tying this together, the complete example of creating a contour plot of the two-dimensional objective function is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 |
# create a contour plot with 50 levels and jet color scheme pyplot.contour(X, y, resultados, 50, alpha=1.0, cmap=‘jet’) # show the plot pyplot.show() Tying esta juntos, la completar ejemplo of creating a contour trama of la dos–dimensional objetivo función es listado abajo. # contour plot for 2d objective function desde numpy import arange desde numpy import meshgrid desde matplotlib import pyplot # objective function def objetivo(X, y): regreso x**2.0 + y**2.0 # define range for input r_min, r_max = –5.0, 5.0 # sample input range uniformly at 0.1 increments xaxis = arange(r_min, r_max, 0.1) yaxis = arange(r_min, r_max, 0.1) # create a mesh from the axis X, y = meshgrid(xaxis, yaxis) # compute targets resultados = objetivo(X, y) # create a contour plot with 50 levels and jet color scheme pyplot.contour(X, y, resultados, 50, alpha=1.0, cmap=‘jet’) # show the plot pyplot.show() |
Running the example creates the contour plot.
We can see that the more curved parts of the surface around the edges have more contours to show the detail, and the less curved parts of the surface in the middle have fewer contours.
We can see that the lowest part of the domain is the middle, as expected.
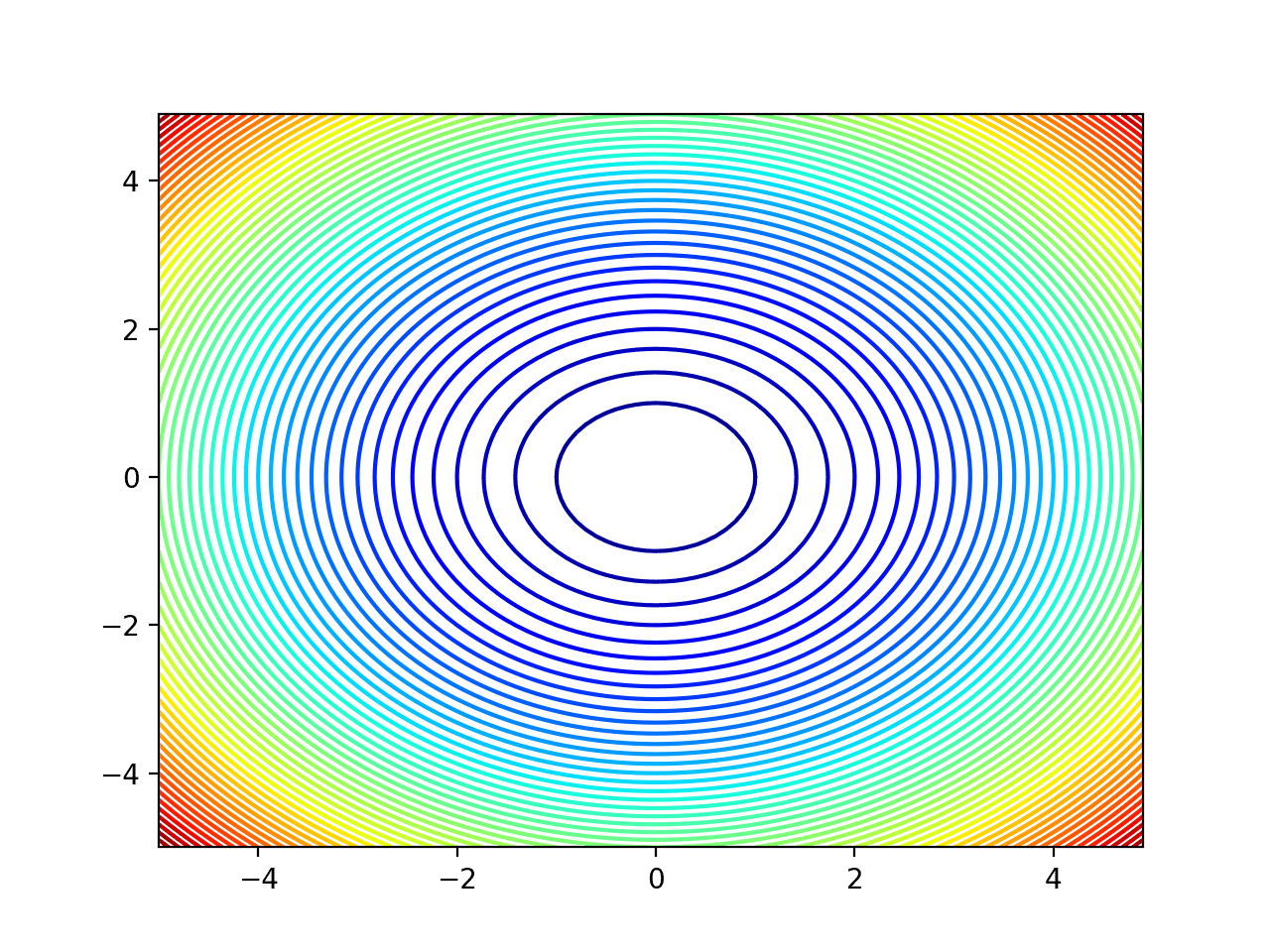
Contour Plot of a Two-Dimensional Objective Function
Filled Contour Plot of Test Function
It is also helpful to color the plot between the contours to show a more complete surface.
Again, the colors are just a simple linear interpolation, not the true function evaluation. This must be kept in mind on more complex functions where fine detail will not be shown.
We can fill the contour plot using the contourf() version of the function that takes the same arguments.
|
... # create a filled contour plot with 50 levels and jet color scheme pyplot.contourf(X, y, resultados, niveles=50, cmap=‘jet’) |
We can also show the optima on the plot, in this case as a white star that will stand out against the blue background color of the lowest part of the plot.
|
... # define the known function optima optima_x = [[0.0, 0.0] # draw the function optima as a white star pyplot.trama([[optima_x[[0]], [[optima_x[[1]], ‘*’, color=‘white’) |
Tying this together, the complete example of a filled contour plot with the optima marked is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 |
# filled contour plot for 2d objective function and show the optima desde numpy import arange desde numpy import meshgrid desde matplotlib import pyplot # objective function def objetivo(X, y): regreso x**2.0 + y**2.0 # define range for input r_min, r_max = –5.0, 5.0 # sample input range uniformly at 0.1 increments xaxis = arange(r_min, r_max, 0.1) yaxis = arange(r_min, r_max, 0.1) # create a mesh from the axis X, y = meshgrid(xaxis, yaxis) # compute targets resultados = objetivo(X, y) # create a filled contour plot with 50 levels and jet color scheme pyplot.contourf(X, y, resultados, niveles=50, cmap=‘jet’) # define the known function optima optima_x = [[0.0, 0.0] # draw the function optima as a white star pyplot.trama([[optima_x[[0]], [[optima_x[[1]], ‘*’, color=‘white’) # show the plot pyplot.show() |
Running the example creates the filled contour plot that gives a better idea of the shape of the objective function.
The optima at [x=0, y=0] is then marked clearly with a white star.
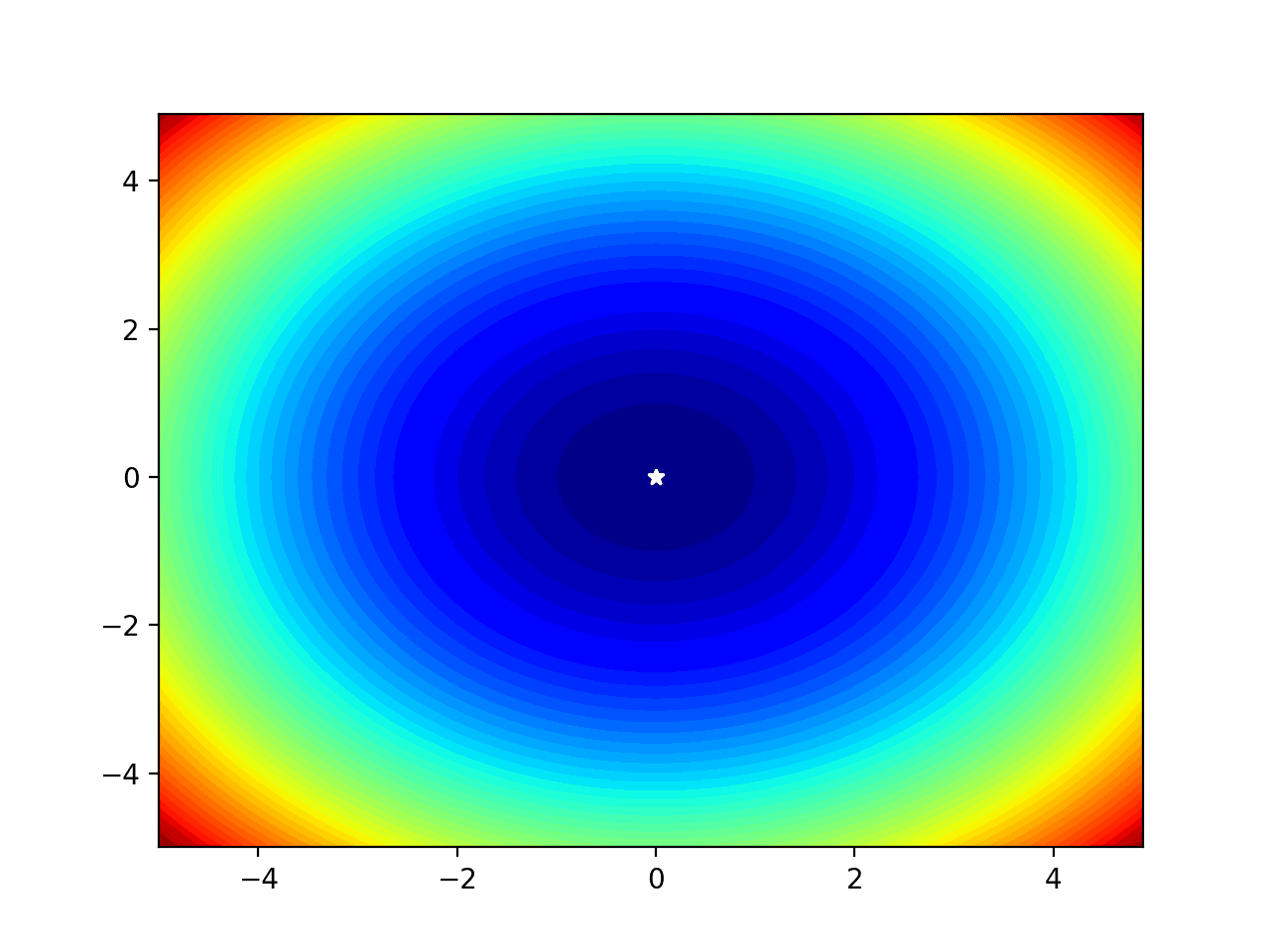
Filled Contour Plot of a Two-Dimensional Objective Function With Optima Marked by a White Star
Filled Contour Plot of Test Function with Samples
We may want to show the progress of an optimization algorithm to get an idea of its behavior in the context of the shape of the objective function.
In this case, we can simulate the points chosen by an optimization algorithm with random coordinates in the input space.
|
... # simulate a sample made by an optimization algorithm semilla(1) sample_x = r_min + rand(10) * (r_max – r_min) sample_y = r_min + rand(10) * (r_max – r_min) |
These points can then be plotted directly as black circles and their context color can give an idea of their relative quality.
|
... # plot the sample as black circles pyplot.trama(sample_x, sample_y, ‘o’, color=‘black’) |
Tying this together, the complete example of a filled contour plot with optimal and input sample plotted is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
# filled contour plot for 2d objective function and show the optima and sample desde numpy import arange desde numpy import meshgrid desde numpy.random import semilla desde numpy.random import rand desde matplotlib import pyplot # objective function def objetivo(X, y): regreso x**2.0 + y**2.0 # define range for input r_min, r_max = –5.0, 5.0 # sample input range uniformly at 0.1 increments xaxis = arange(r_min, r_max, 0.1) yaxis = arange(r_min, r_max, 0.1) # create a mesh from the axis X, y = meshgrid(xaxis, yaxis) # compute targets resultados = objetivo(X, y) # simulate a sample made by an optimization algorithm semilla(1) sample_x = r_min + rand(10) * (r_max – r_min) sample_y = r_min + rand(10) * (r_max – r_min) # create a filled contour plot with 50 levels and jet color scheme pyplot.contourf(X, y, resultados, niveles=50, cmap=‘jet’) # define the known function optima optima_x = [[0.0, 0.0] # draw the function optima as a white star pyplot.trama([[optima_x[[0]], [[optima_x[[1]], ‘*’, color=‘white’) # plot the sample as black circles pyplot.trama(sample_x, sample_y, ‘o’, color=‘black’) # show the plot pyplot.show() |
Running the example, we can see the filled contour plot as before with the optima marked.
We can now see the sample drawn as black dots and their surrounding color and relative distance to the optima gives an idea of how close the algorithm (random points in this case) got to solving the problem.
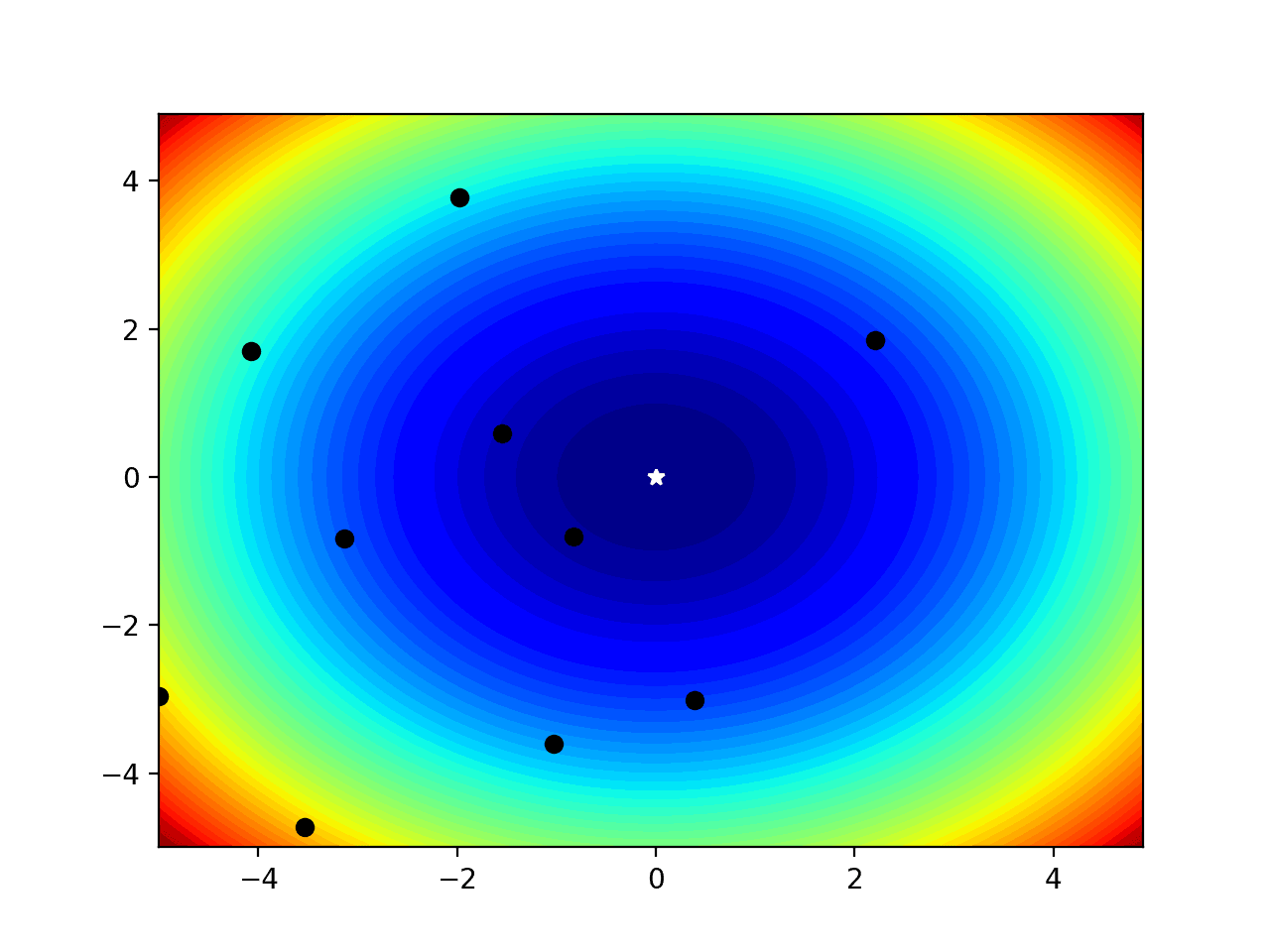
Filled Contour Plot of a Two-Dimensional Objective Function With Optima and Input Sample Marked
Surface Plot of Test Function
Finally, we may want to create a three-dimensional plot of the objective function to get a fuller idea of the curvature of the function.
This can be achieved using the plot_surface() Matplotlib function, that, like the contour plot, takes the mesh grid and function evaluation directly.
|
... # create a surface plot with the jet color scheme figura = pyplot.figura() eje = figura.gca(projection=‘3d’) eje.plot_surface(X, y, resultados, cmap=‘jet’) |
The complete example of creating a surface plot is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 |
# surface plot for 2d objective function desde numpy import arange desde numpy import meshgrid desde matplotlib import pyplot desde mpl_toolkits.mplot3d import Axes3D # objective function def objetivo(X, y): regreso x**2.0 + y**2.0 # define range for input r_min, r_max = –5.0, 5.0 # sample input range uniformly at 0.1 increments xaxis = arange(r_min, r_max, 0.1) yaxis = arange(r_min, r_max, 0.1) # create a mesh from the axis X, y = meshgrid(xaxis, yaxis) # compute targets resultados = objetivo(X, y) # create a surface plot with the jet color scheme figura = pyplot.figura() eje = figura.gca(projection=‘3d’) eje.plot_surface(X, y, resultados, cmap=‘jet’) # show the plot pyplot.show() |
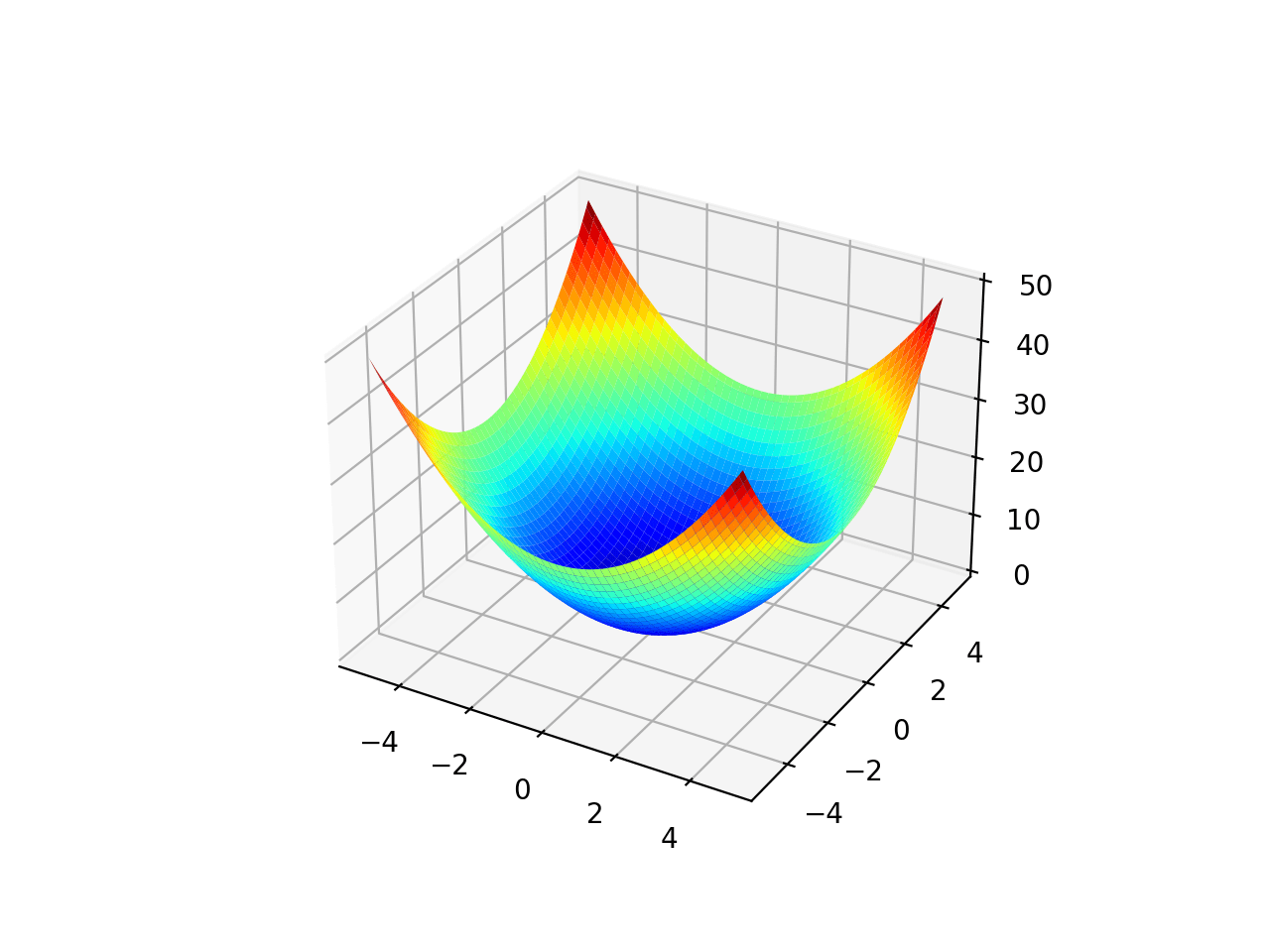
Running the example creates a three-dimensional surface plot of the objective function.

Surface Plot of a Two-Dimensional Objective Function
Additionally, the plot is interactive, meaning that you can use the mouse to drag the perspective on the surface around and view it from different angles.
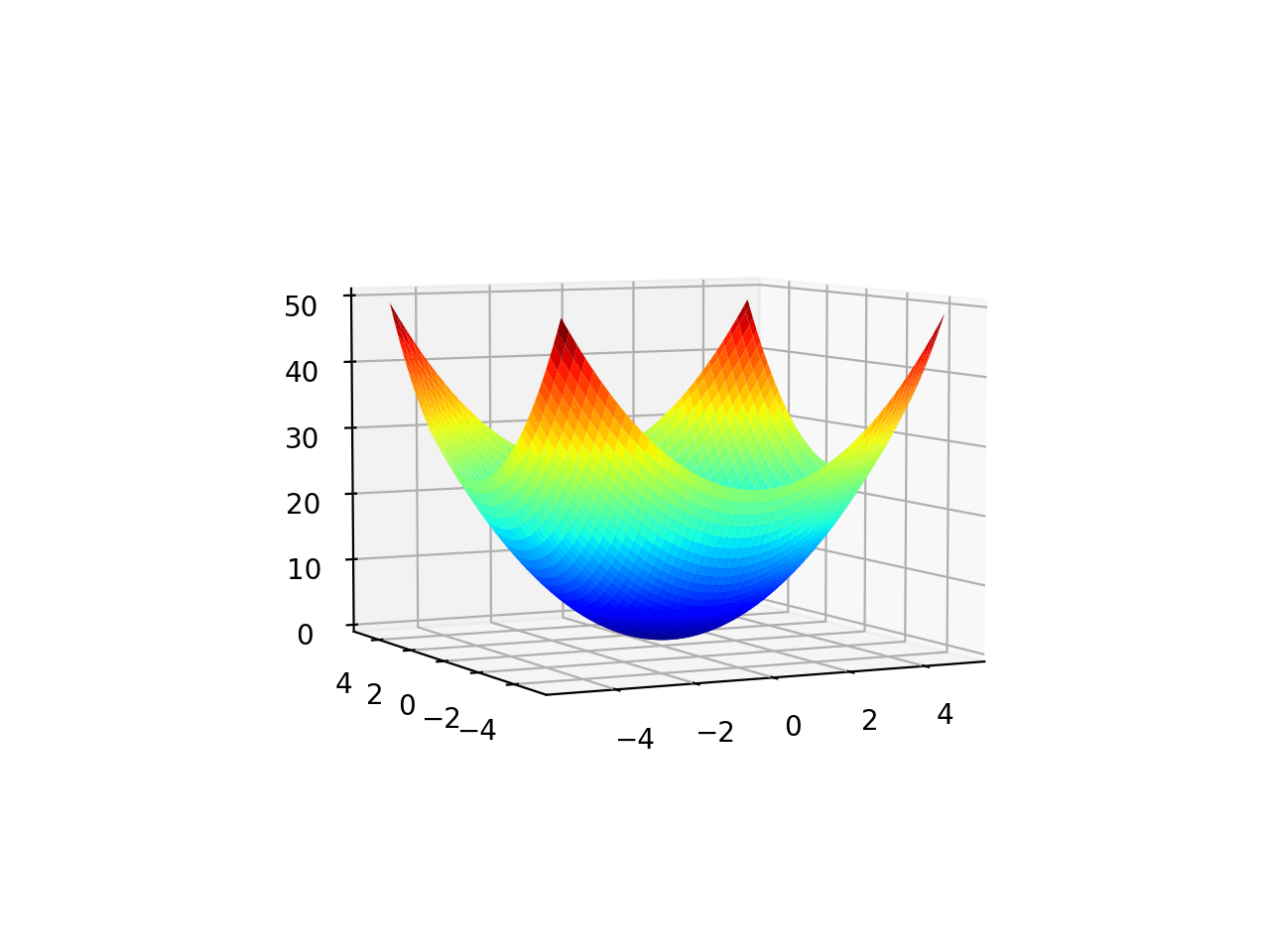
Surface Plot From a Different Angle of a Two-Dimensional Objective Function
Further Reading
This section provides more resources on the topic if you are looking to go deeper.
APIs
Articles
Summary
In this tutorial, you discovered how to create visualizations for function optimization in Python.
Specifically, you learned:
- Visualization is an important tool when studying function optimization algorithms.
- How to visualize one-dimensional functions and samples using line plots.
- How to visualize two-dimensional functions and samples using contour and surface plots.
Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.
