Figura 1. Medidas de rendimiento de generalización para redes neuronales entrenadas en cuatro funciones booleanas diferentes (colores) con tamaño de conjunto de entrenamiento variable. Tanto para MSE (izquierda) como para la capacidad de aprendizaje (derecha), las predicciones teóricas (curvas) coinciden estrechamente con el rendimiento real (puntos).
El aprendizaje profundo ha demostrado ser un éxito asombroso para innumerables problemas de interés, pero este éxito contradice el hecho de que, en un nivel fundamental, no entendemos por qué funciona tan bien. Muchos fenómenos empíricos, bien conocidos por los profesionales del aprendizaje profundo, siguen siendo un misterio para los teóricos. Quizás el mayor de estos misterios ha sido la cuestión de la generalización: ¿Por qué las funciones aprendidas por las redes neuronales se generalizan tan bien a los datos invisibles? Desde la perspectiva del ML clásico, el alto rendimiento de las redes neuronales es una sorpresa dado que están tan sobre parametrizadas que podrían representar fácilmente innumerables funciones que generalizan poco.
Las preguntas que comienzan con «por qué» son difíciles de entender, por lo que abordamos el siguiente problema cuantitativo: dada una arquitectura de red, una función objetivo $ f $ y un conjunto de entrenamiento de $ n $ ejemplos aleatorios, ¿podemos predecir eficientemente el rendimiento de generalización de la función aprendida de la red $ hat {f} $? Una teoría que haga esto no solo explicaría por qué las redes neuronales se generalizan bien en ciertas funciones, sino que también nos diría para qué clases de función es adecuada una arquitectura dada y, potencialmente, incluso nos permitiría elegir la mejor arquitectura para un problema dado desde los primeros principios, como además de servir como marco general para abordar una gran cantidad de otros misterios del aprendizaje profundo.
Resulta que esto es posible: en nuestro artículo reciente, Derivamos una teoría de primeros principios que permite hacer predicciones precisas de la generalización de redes neuronales. (al menos en ciertos entornos). Para hacerlo, hacemos una cadena de aproximaciones, primero aproximando una red real como una red idealizada de ancho infinito, que se sabe que es equivalente a la regresión del kernel, luego derivando nuevos resultados aproximados para la generalización de la regresión del kernel para producir unos pocos simples ecuaciones que, a pesar de estas aproximaciones, predicen de cerca el rendimiento de generalización de la red original.
Red finita $ approx $ red de ancho infinito $ = $ regresión del kernel
Una de las principales venas de la teoría del aprendizaje profundo en los últimos años ha estudiado las redes neuronales de ancho infinito. Uno podría suponer que agregar más parámetros a una red solo haría que sea más difícil de entender, pero, por resultados similares a los teoremas del límite central para redes neuronales, las redes de ancho infinito en realidad toman formas analíticas muy simples. En particular, una red amplia entrenada por descenso de gradiente a pérdida cero de MSE siempre aprenderá la función
donde $ mathcal {D} $ es el conjunto de datos, $ f $ y $ hat {f} $ son las funciones objetivo y aprendidas respectivamente, y $ K $ es el “núcleo tangente neuronal” (NTK) de la red. Esta es una ecuación matricial: $ K (x, mathcal {D}) $ es un vector de fila, $ K ( mathcal {D}, mathcal {D}) $ es la «matriz del núcleo» y $ f ( mathcal {D}) $ es un vector de columna. El NTK es diferente para cada clase de arquitectura, pero (al menos para redes amplias) es el mismo cada vez que inicializa. Debido a la similitud de esta ecuación con la ecuación normal de regresión lineal, recibe el nombre de «regresión del núcleo».
La pura simplicidad de esta ecuación podría hacer sospechar que una red de ancho infinito es una idealización absurda con poca semejanza con las redes útiles, pero los experimentos muestran que, al igual que con el teorema del límite central regular, los resultados de ancho infinito generalmente se activan antes que usted. esperaría, en anchos de solo cientos. Confiando en que esta primera aproximación tendrá peso, nuestro desafío ahora es comprender la regresión del kernel.
Aproximación de la generalización de la regresión del kernel
Al derivar la generalización de la regresión del kernel, obtenemos mucho provecho de un truco simple: observamos el problema de aprendizaje en la base propia del kernel. Visto como un operador lineal, el kernel tiene pares de valor propio / vector $ ( lambda_i, phi_i) $ definidos por la condición de que
[intlimits_{text{input space}} ! ! ! ! ! ! K(x, x’) phi_i(x’) d x’ = lambda_i phi_i(x).]Hablando intuitivamente, un kernel es una función de similitud, y podemos interpretar sus funciones propias de alto valor propio como mapeo de puntos «similares» a valores similares.
La pieza central de nuestro análisis es una medida de generalización que llamamos «capacidad de aprendizaje» que cuantifica la alineación de $ f $ y $ hat {f} $. Con algunas aproximaciones menores, obtenemos el resultado extremadamente simple de que la capacidad de aprendizaje de cada función propia viene dada por
[mathcal{L}(phi_i) = frac{lambda_i}{lambda_i + C},]donde $ C $ es una constante. Una mayor capacidad de aprendizaje es mejor y, por lo tanto, esta fórmula nos dice que Las funciones propias de valores propios superiores son más fáciles de aprender. Además, mostramos que, a medida que se agregan ejemplos al conjunto de entrenamiento, $ C $ disminuye gradualmente de $ infty $ a $ 0 $, lo que significa que el $ mathcal {L} ( phi_i) $ de cada modo aumenta gradualmente desde $ 0 $ a $ 1 $, con los modos propios superiores aprendidos primero. Los modelos de esta forma tienen un fuerte sesgo inductivo hacia el aprendizaje de modos propios superiores.
En última instancia, derivamos expresiones no solo para la capacidad de aprendizaje, sino para todas las estadísticas de primer y segundo orden de la función aprendida, incluida la recuperación de expresiones anteriores para MSE. Encontramos que estas expresiones son bastante precisas no solo para la regresión del núcleo, sino también para las redes finitas, como se ilustra en la Figura 1.
No hay almuerzo gratis para redes neuronales
Además de las aproximaciones para el rendimiento de la generalización, también probamos un resultado exacto simple que llamamos el «teorema de no almuerzo gratis para la regresión del kernel». El teorema clásico de no almuerzo gratis para los algoritmos de aprendizaje establece aproximadamente que, promediado sobre todas las funciones objetivo posibles $ f $, cualquier algoritmo de aprendizaje supervisado tiene el mismo rendimiento de generalización esperado. Esto tiene sentido intuitivo; después de todo, la mayoría de las funciones parecen ruido blanco, sin patrones discernibles, pero tampoco es muy útil ya que el conjunto de «todas las funciones» suele ser enorme. Nuestra extensión, específica para la regresión del kernel, esencialmente establece que
[begin{align}sum_i mathcal{L}(phi_i) = text{[training set size]}. end {align} ]
Es decir, la suma de las capacidades de aprendizaje en todas las funciones propias del kernel es igual al tamaño del conjunto de entrenamiento. Este resultado exacto pinta una imagen vívida del sesgo inductivo de un kernel: el kernel tiene exactamente $ text {[training set size]} $ unidades de capacidad de aprendizaje para distribuir en sus modos propios, ni más, ni menos, y por lo tanto los modos propios están bloqueados en una competencia de suma cero para aprender. Como se muestra en la Figura 2, encontramos que esta ley de conservación básica se cumple exactamente para la regresión NTK e incluso aproximadamente para redes finitas. Hasta donde sabemos, este es el primer resultado que cuantifica tal compensación en la regresión del kernel o el aprendizaje profundo. También se aplica a la regresión lineal, un caso especial de regresión del kernel.
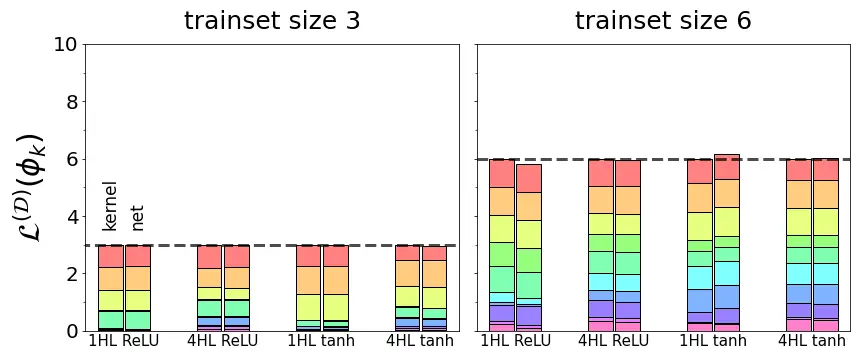
Figura 2. Para cuatro arquitecturas de red diferentes (redes $ text {ReLU} $ y $ text {tanh} $ completamente conectadas con una o cuatro capas ocultas), la capacidad de aprendizaje total sumada en todas las funciones propias es igual al tamaño del conjunto de entrenamiento. Los componentes coloreados muestran las aptitudes de aprendizaje de las funciones propias individuales. Para la regresión del kernel con el NTK de la red (barra izquierda en cada par), la suma es exactamente el tamaño del tren, mientras que las redes entrenadas reales (barra derecha en cada par) suman aproximadamente el tamaño del tren.
Conclusión
Estos resultados muestran que, a pesar de la notoria inescrutabilidad de las redes neuronales, podemos esperar entender cuándo y por qué funcionan bien. Como en otros campos de la ciencia, si damos un paso atrás, podemos encontrar reglas simples que gobiernan lo que ingenuamente parecen ser sistemas de complejidad incomprensible. Ciertamente, queda mucho trabajo por hacer antes de que entendamos realmente el aprendizaje profundo: nuestra teoría solo se aplica a la pérdida de MSE, y el sistema propio de NTK aún se desconoce en todos los casos, excepto en los más simples, pero nuestros resultados hasta ahora sugieren que tenemos los ingredientes de una buena fe. teoría de la generalización de redes neuronales en nuestras manos.
Esta publicación se basa en el artículo «Los valores propios del núcleo tangente neuronal predice con precisión la generalización», que es un trabajo conjunto con la compañera de laboratorio Maddie Dickens y el asesor Mike DeWeese. Proporcionamos código para reproducir todos nuestros resultados. Estaremos encantados de responder a sus preguntas o comentarios.
