Una suave introducción al jacobiano

En la literatura, el término Jacobiano a menudo se usa indistintamente para referirse tanto a la matriz jacobiana como a su determinante.

Tanto la matriz como el determinante tienen aplicaciones útiles e importantes: en el aprendizaje automático, la matriz jacobiana agrega las derivadas parciales que son necesarias para la retropropagación; el determinante es útil en el proceso de cambio entre variables.

En este tutorial, revisarás una suave introducción al jacobiano.

Después de completar este tutorial, sabrá:

La matriz jacobiana recopila todas las derivadas parciales de primer orden de una función multivariante que se puede utilizar para retropropagación.
El determinante jacobiano es útil para cambiar entre variables, donde actúa como un factor de escala entre un espacio de coordenadas y otro.

Empecemos.

Una suave introducción al jacobiano
Foto de Simon Berger, algunos derechos reservados.

Descripción general del tutorial

Este tutorial se divide en tres partes; ellos son:

Derivadas parciales en el aprendizaje automático
La matriz jacobiana
Otros usos del jacobiano

Derivadas parciales en el aprendizaje automático

Hasta ahora hemos mencionado que los gradientes y las derivadas parciales son importantes para que un algoritmo de optimización actualice, digamos, los pesos del modelo de una red neuronal para alcanzar un conjunto óptimo de pesos. El uso de derivadas parciales permite actualizar cada ponderación independientemente de las demás, calculando el gradiente de la curva de error con respecto a cada ponderación a su vez.

Muchas de las funciones con las que solemos trabajar en el aprendizaje automático son funciones multivariadas con valores vectoriales, lo que significa que mapean múltiples entradas reales, norte, a múltiples salidas reales, metro:

Por ejemplo, considere una red neuronal que clasifica imágenes en escala de grises en varias clases. La función que está siendo implementada por tal clasificador mapearía el norte valores de píxeles de cada imagen de entrada de un solo canal, para metro probabilidades de salida de pertenencia a cada una de las diferentes clases.

En el entrenamiento de una red neuronal, el algoritmo de retropropagación se encarga de compartir el error calculado en la capa de salida, entre las neuronas que componen las diferentes capas ocultas de la red neuronal, hasta llegar a la entrada.

El principio fundamental del algoritmo de retropropagación al ajustar los pesos en una red es que cada peso en una red debe actualizarse en proporción a la sensibilidad del error general de la red a los cambios en ese peso.

– Página 222, Deep Learning, 2019.

Esta sensibilidad del error general de la red a cambios en cualquier peso particular se mide en términos de la tasa de cambio, que, a su vez, se calcula tomando la derivada parcial del error con respecto al mismo peso.

Para simplificar, suponga que una de las capas ocultas de alguna red en particular consta de una sola neurona, k. Podemos representar esto en términos de un gráfico computacional simple:

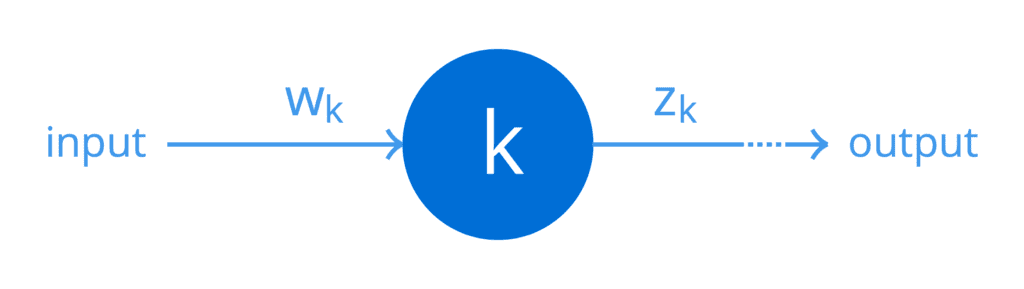
Una neurona con una sola entrada y una sola salida

De nuevo, por simplicidad, supongamos que un peso, w_k, se aplica a una entrada de esta neurona para producir una salida, z_k, según la función que implemente esta neurona (incluida la no linealidad). Luego, el peso de esta neurona se puede conectar al error en la salida de la red de la siguiente manera (la siguiente fórmula se conoce formalmente como regla de la cadena del cálculo, pero más sobre esto más adelante en un tutorial separado):

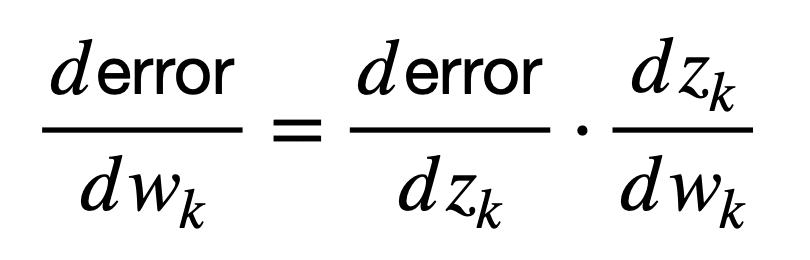
Aquí, la derivada, dz_k / dw_k, primero conecta el peso, w_k, a la salida, z_k, mientras que la derivada, Derror / dz_k, posteriormente conecta la salida, z_k, al error de red.

Es más frecuente que tengamos muchas neuronas conectadas que pueblan la red, a cada una de las cuales se le atribuye un peso diferente. Dado que estamos más interesados en tal escenario, entonces podemos generalizar más allá del caso escalar para considerar múltiples entradas y múltiples salidas:

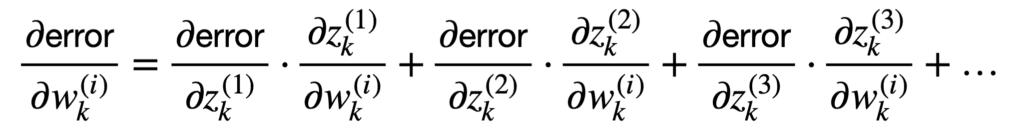
Esta suma de términos se puede representar de manera más compacta de la siguiente manera:

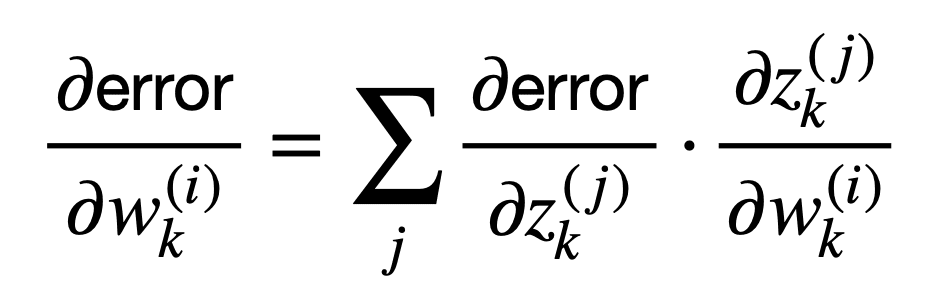
O, de manera equivalente, en notación vectorial usando el operador del, ∇, para representar el gradiente del error con respecto a los pesos, w_k, o las salidas, z_k:

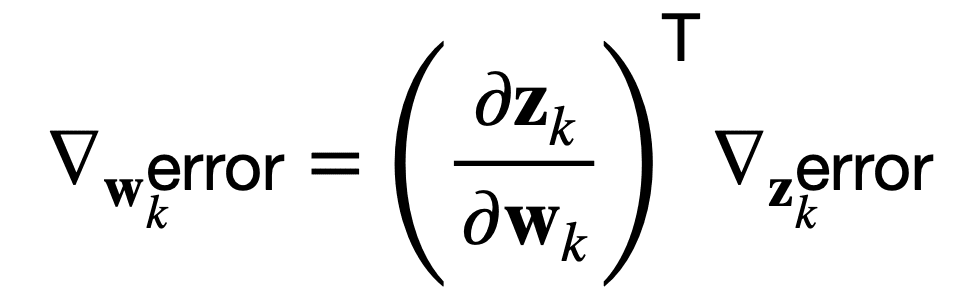
El algoritmo de retropropagación consiste en realizar un producto de gradiente jacobiano para cada operación en el gráfico.

– Página 207, Deep Learning, 2017.

Esto significa que el algoritmo de retropropagación puede relacionar la sensibilidad del error de red a cambios en los pesos, a través de una multiplicación por el Matriz jacobiana, (∂z_k / ∂w_k)^T.

Por tanto, ¿qué contiene esta matriz jacobiana?

La matriz jacobiana

La matriz jacobiana recopila todas las derivadas parciales de primer orden de una función multivariante.

Específicamente, considere primero una función que mapea tu entradas reales, a una única salida real:

Entonces, para un vector de entrada, X, de longitud, tu, el vector jacobiano de tamaño, tu × 1, se puede definir de la siguiente manera:

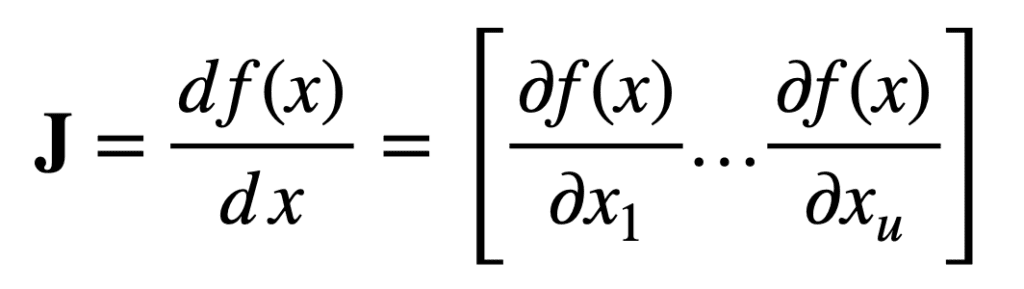
Ahora, considere otra función que mapea tu entradas reales, a v salidas reales:

Entonces, para el mismo vector de entrada, X, de longitud, tu, el jacobiano es ahora un tu × v matriz, J ∈ ℝ^{u ×}^v, que se define de la siguiente manera:

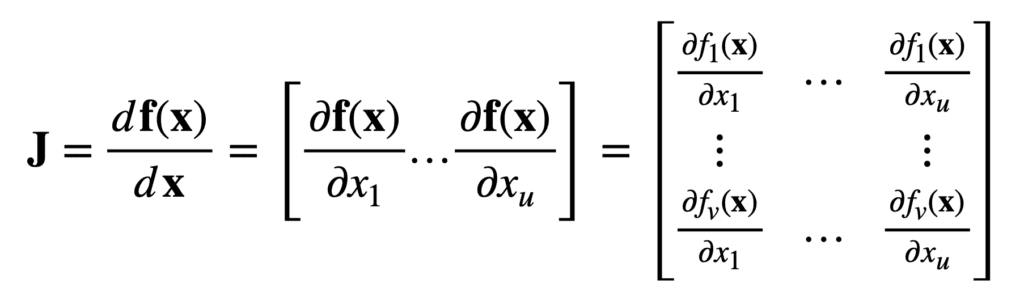
Reencuadrar la matriz jacobiana en el problema de aprendizaje automático considerado anteriormente, conservando el mismo número de tu entradas reales y v salidas reales, encontramos que esta matriz contendría las siguientes derivadas parciales:

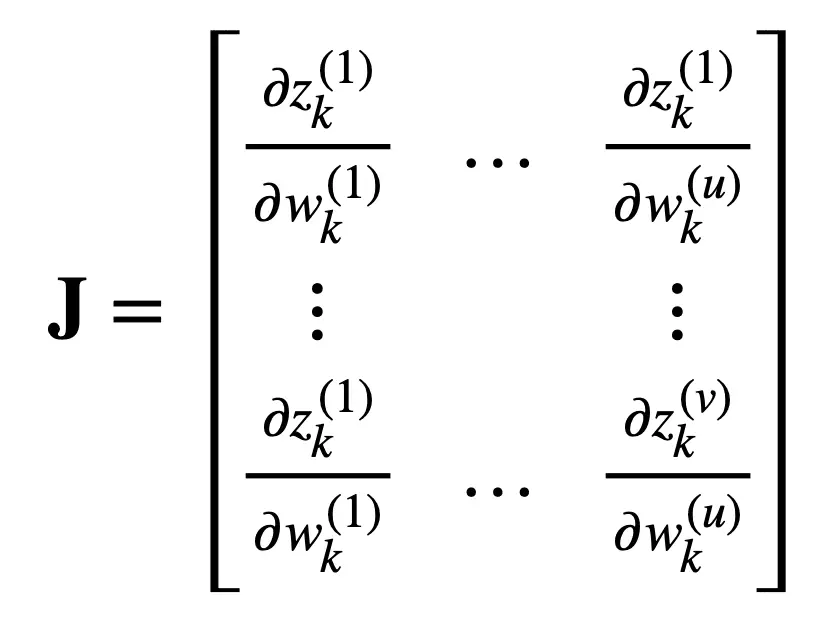
Otros usos del jacobiano

Una técnica importante cuando se trabaja con integrales implica la cambio de variables (también conocido como, integración por sustitución o sustitución-u), donde una integral se simplifica en otra integral que es más fácil de calcular.

En el caso de una sola variable, sustituyendo alguna variable, X, con otra variable, tu, puede transformar la función original en una más simple para la que es más fácil encontrar una antiderivada. En el caso de dos variables, una razón adicional podría ser que también desearíamos transformar la región de términos sobre los que nos estamos integrando, en una forma diferente.

En el caso de una sola variable, normalmente solo hay una razón para querer cambiar la variable: hacer que la función sea más «agradable» para que podamos encontrar una antiderivada. En el caso de dos variables, hay una segunda razón potencial: la región bidimensional sobre la que necesitamos integrarnos es de alguna manera desagradable, y queremos que la región en términos de u y v sea más agradable, que sea un rectángulo, por ejemplo .

– Página 412, Cálculo simple y multivariable, 2020.

Cuando se realiza una sustitución entre dos (o posiblemente más) variables, el proceso comienza con una definición de las variables entre las cuales se producirá la sustitución. Por ejemplo, X = F(tu, v) y y = gramo(tu, v). Esto es seguido por una conversión de los límites integrales dependiendo de cómo funcionan, F y gramo, transformará el tu–v avión en el X–y avión. Finalmente, el valor absoluto de la Determinante jacobiano se calcula e incluye, para actuar como un factor de escala entre un espacio de coordenadas y otro.

Otras lecturas

Esta sección proporciona más recursos sobre el tema si desea profundizar.

Libros

Artículos

Resumen

En este tutorial, descubrió una suave introducción al jacobiano.

Específicamente, aprendiste:

La matriz jacobiana recopila todas las derivadas parciales de primer orden de una función multivariante que se puede utilizar para retropropagación.
El determinante jacobiano es útil para cambiar entre variables, donde actúa como un factor de escala entre un espacio de coordenadas y otro.

¿Tiene usted alguna pregunta?
Haga sus preguntas en los comentarios a continuación y haré todo lo posible para responder.