Última actualización el 27 de abril de 2021
Selección dinámica de conjuntos es una técnica de aprendizaje por conjuntos que selecciona automáticamente un subconjunto de miembros del conjunto justo a tiempo al hacer una predicción.
La técnica implica ajustar varios modelos de aprendizaje automático en el conjunto de datos de entrenamiento y luego seleccionar los modelos que se espera que tengan un mejor rendimiento al hacer una predicción para un nuevo ejemplo específico, según los detalles del ejemplo que se va a predecir.
Esto se puede lograr usando un modelo de vecino k-más cercano para ubicar ejemplos en el conjunto de datos de entrenamiento que están más cerca del nuevo ejemplo que se va a predecir, evaluando todos los modelos en el grupo en este vecindario y usando los modelos que funcionan mejor en el vecindario para haga una predicción para el nuevo ejemplo.
Como tal, la selección de conjuntos dinámicos a menudo puede funcionar mejor que cualquier modelo individual en el grupo y mejor que promediar todos los miembros del grupo, la denominada selección de conjuntos estáticos.
En este tutorial, descubrirá cómo desarrollar modelos de selección de conjuntos dinámicos en Python.
Después de completar este tutorial, sabrá:
- Los algoritmos de selección de conjuntos dinámicos eligen automáticamente los miembros del conjunto al hacer una predicción sobre nuevos datos.
- Cómo desarrollar y evaluar modelos de selección de conjuntos dinámicos para tareas de clasificación utilizando la API scikit-learn.
- Cómo explorar el efecto de los hiperparámetros del modelo de selección de conjuntos dinámicos sobre la precisión de la clasificación.
Pon en marcha tu proyecto con mi nuevo libro Ensemble Learning Algorithms With Python, que incluye tutoriales paso a paso y el Código fuente de Python archivos para todos los ejemplos.
Empecemos.

Selección dinámica de conjuntos (DES) en Python
Foto de Simon Harrod, algunos derechos reservados.
Descripción general del tutorial
Este tutorial se divide en tres partes; ellos son:
- Selección dinámica de conjuntos
- k-Oracle vecino más cercano (KNORA) con Scikit-Learn
- KNORA-Eliminar (KNORA-E)
- KNORA-Unión (KNORA-U)
- Ajuste de hiperparámetros para KNORA
- Explore k en k-Vecino más cercano
- Explore los algoritmos para el grupo de clasificadores
Selección dinámica de conjuntos
Los sistemas de clasificación múltiple se refieren a un campo de algoritmos de aprendizaje automático que utilizan varios modelos para abordar problemas de modelado predictivo de clasificación.
La primera clase de sistemas de clasificación múltiple que tiene éxito se conoce como Selección de clasificador dinámico o DCS para abreviar.
- Selección de clasificador dinámico: Algoritmos que eligen dinámicamente uno entre muchos modelos entrenados para hacer una predicción basada en los detalles específicos de la entrada.
Los algoritmos de selección de clasificador dinámico generalmente implican dividir el espacio de características de entrada de alguna manera y asignar modelos específicos para que sean responsables de hacer predicciones para cada partición. Existe una variedad de algoritmos DCS diferentes y los esfuerzos de investigación se centran principalmente en cómo evaluar y asignar clasificadores a regiones específicas del espacio de entrada.
Después de capacitar a varios alumnos individuales, DCS selecciona dinámicamente un alumno para cada instancia de prueba. […] DCS hace predicciones utilizando un alumno individual.
– Página 93, Métodos de conjunto: fundamentos y algoritmos, 2012.
Una extensión natural de DCS son los algoritmos que seleccionan uno o más modelos dinámicamente para hacer una predicción. Es decir, seleccionar un subconjunto o conjunto de clasificadores de forma dinámica. Estas técnicas se denominan selección dinámica de conjuntos o DES.
- Selección dinámica de conjuntos: Algoritmos que eligen dinámicamente un subconjunto de modelos entrenados para hacer una predicción basada en los detalles específicos de la entrada.
Los algoritmos de selección dinámica de conjuntos funcionan de manera muy similar a los algoritmos DCS, excepto que las predicciones se realizan utilizando votos de múltiples modelos de clasificadores en lugar de un único mejor modelo. En efecto, cada región del espacio de características de entrada pertenece a un subconjunto de modelos que funcionan mejor en esa región.
… dado el hecho de que seleccionar un solo clasificador puede ser muy propenso a errores, algunos investigadores decidieron seleccionar un subconjunto del grupo de clasificadores en lugar de un solo clasificador base. Todos los clasificadores base que obtuvieron un cierto nivel de competencia se utilizan para componer la EdC, y sus resultados se agregan para predecir la etiqueta …
– Selección dinámica de clasificadores: avances y perspectivas recientes, 2018.
Quizás el enfoque canónico para la selección de conjuntos dinámicos es el algoritmo k-Oráculo vecino más cercano, o KNORA, ya que es una extensión natural del algoritmo canónico de selección del clasificador dinámico «Precisión local de selección de clasificador dinámico, ”O DCS-LA.
DCS-LA implica seleccionar los k vecinos más cercanos del conjunto de datos de entrenamiento o validación para un nuevo patrón de entrada dado, luego seleccionar el mejor clasificador individual en función de su desempeño en ese vecindario de k ejemplos para hacer una predicción sobre el nuevo ejemplo.
KNORA fue descrito por Albert Ko, et al. en su artículo de 2008 titulado «De la selección dinámica de clasificadores a la selección dinámica de conjuntos». Es una extensión de DCS-LA que selecciona múltiples modelos que funcionan bien en el vecindario y cuyas predicciones luego se combinan usando la votación por mayoría para hacer una predicción de salida final.
Para cualquier punto de datos de prueba, KNORA simplemente encuentra sus vecinos K más cercanos en el conjunto de validación, determina qué clasificadores clasifican correctamente a esos vecinos en el conjunto de validación y los usa como el conjunto para clasificar el patrón dado en ese conjunto de prueba.
– De la selección dinámica de clasificadores a la selección dinámica de conjuntos, 2008.
Los modelos de clasificador seleccionados se denominan «oráculos“, De ahí el uso de oráculo en nombre del método.
El conjunto se considera dinámico porque los miembros se eligen justo a tiempo condicional en el patrón de entrada específico que requiere una predicción. Esto se opone a estático, donde los miembros del conjunto se eligen una vez, como promediar las predicciones de todos los clasificadores en el modelo.
Esto se hace de manera dinámica, ya que diferentes patrones pueden requerir diferentes conjuntos de clasificadores. Por lo tanto, llamamos a nuestro método una selección de conjunto dinámica.
– De la selección dinámica de clasificadores a la selección dinámica de conjuntos, 2008.
Se describen dos versiones de KNORA, incluidas KNORA-Eliminate y KNORA-Union.
- KNORA-Eliminar (KNORA-E): Conjunto de clasificadores que logra una precisión perfecta en la vecindad del nuevo ejemplo, con un tamaño de vecindad reductor hasta que se localiza al menos un clasificador perfecto.
- KNORA-Unión (KNORA-U): Conjunto de todos los clasificadores que hace al menos una predicción correcta sobre el vecindario con votación ponderada y votos proporcionales a la precisión en el vecindario.
KNORA-Eliminar, o KNORA-E para abreviar, implica seleccionar todos los clasificadores que logran predicciones perfectas en la vecindad de k ejemplos en la vecindad. Si ningún clasificador alcanza el 100 por ciento de precisión, el tamaño del vecindario se reduce en uno y los modelos se vuelven a evaluar. Este proceso se repite hasta que se descubren uno o más modelos que tienen un rendimiento perfecto, y luego se utilizan para hacer una predicción para el nuevo ejemplo.
En el caso de que ningún clasificador pueda clasificar correctamente a todos los K vecinos más cercanos del patrón de prueba, simplemente disminuimos el valor de K hasta que al menos un clasificador clasifique correctamente a sus vecinos.
– De la selección dinámica de clasificadores a la selección dinámica de conjuntos, 2008.
KNORA-Unión, o KNORA-U para abreviar, implica seleccionar todos los clasificadores que hacen al menos una predicción correcta en el vecindario. Las predicciones de cada clasificador luego se combinan usando un promedio ponderado, donde el número de predicciones correctas en el vecindario indica el número de votos asignados a cada clasificador.
Cuantos más vecinos clasifique correctamente un clasificador, más votos tendrá este clasificador para un patrón de prueba
– De la selección dinámica de clasificadores a la selección dinámica de conjuntos, 2008.
Ahora que estamos familiarizados con DES y el algoritmo KNORA, veamos cómo podemos usarlo en nuestros propios proyectos de modelado predictivo de clasificación.
¿Quiere comenzar con el aprendizaje por conjuntos?
Realice ahora mi curso intensivo gratuito de 7 días por correo electrónico (con código de muestra).
Haga clic para registrarse y obtener también una versión gratuita en formato PDF del curso.
Descarga tu minicurso GRATIS
k-Oracle vecino más cercano (KNORA) con Scikit-Learn
Dynamic Ensemble Library, o DESlib para abreviar, es una biblioteca de aprendizaje automático de Python que proporciona una implementación de muchos clasificadores dinámicos diferentes y algoritmos de selección de conjuntos dinámicos.
DESlib es una biblioteca de aprendizaje por conjuntos fácil de usar que se centra en la implementación de técnicas de vanguardia para el clasificador dinámico y la selección de conjuntos.
Primero, podemos instalar la biblioteca DESlib usando el administrador de paquetes pip, si aún no está instalado.
Una vez instalada, podemos verificar que la biblioteca se instaló correctamente y está lista para ser utilizada cargando la biblioteca e imprimiendo la versión instalada.
|
# comprobar la versión de deslib importar deslib impresión(deslib.__versión__) |
La ejecución del script imprimirá su versión de la biblioteca DESlib que ha instalado.
Tu versión debe ser igual o superior. De lo contrario, debe actualizar su versión de la biblioteca DESlib.
DESlib proporciona una implementación del algoritmo KNORA con cada técnica de selección de conjuntos dinámicos a través de las clases KNORAE y KNORAU respectivamente.
Cada clase se puede utilizar directamente como modelo de scikit-learn, lo que permite utilizar directamente el conjunto completo de preparación de datos de scikit-learn, canalizaciones de modelado y técnicas de evaluación de modelos.
Ambas clases usan un algoritmo de vecino k-más cercano para seleccionar el vecino con un valor predeterminado de k = 7.
Se utiliza un conjunto de agregación de bootstrap (ensacado) de árboles de decisión como grupo de modelos de clasificador considerados para cada clasificación que se realiza de forma predeterminada, aunque esto se puede cambiar configurando “clasificadores_piscina”A una lista de modelos.
Podemos usar la función make_classification () para crear un problema de clasificación binario sintético con 10,000 ejemplos y 20 características de entrada.
|
# conjunto de datos sintéticos de clasificación binaria de sklearn.conjuntos de datos importar fabricar_clasificación # definir conjunto de datos X, y = make_classification(n_samples=10000, n_features=20, n_informativo=15, n_redundante=5, estado_aleatorio=7) # resumir el conjunto de datos impresión(X.forma, y.forma) |
La ejecución del ejemplo crea el conjunto de datos y resume la forma de los componentes de entrada y salida.
Ahora que estamos familiarizados con la API DESlib, veamos cómo usar cada algoritmo KNORA en nuestro conjunto de datos de clasificación sintética.
KNORA-Eliminar (KNORA-E)
Podemos evaluar un algoritmo de selección de conjuntos dinámicos KNORA-Eliminate en el conjunto de datos sintéticos.
En este caso, usaremos hiperparámetros de modelo predeterminados, incluidos árboles de decisión empaquetados como grupo de modelos de clasificador y un k = 7 para la selección del vecindario local al hacer una predicción.
Evaluaremos el modelo usando validación cruzada estratificada repetida de k-veces con tres repeticiones y 10 pliegues. Informaremos la desviación estándar y media de la precisión del modelo en todas las repeticiones y pliegues.
El ejemplo completo se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 |
# evaluar la selección dinámica de conjuntos dinámicos KNORA-E para clasificación binaria de numpy importar significar de numpy importar std de sklearn.conjuntos de datos importar make_classification de sklearn.model_selection importar cross_val_score de sklearn.model_selection importar Repetido Estratificado KFold de deslib.des.knora_e importar KNORAE # definir conjunto de datos X, y = make_classification(n_samples=10000, n_features=20, n_informativo=15, n_redundante=5, estado_aleatorio=7) # definir el modelo modelo = KNORAE() # definir el procedimiento de evaluación CV = Repetido Estratificado KFold(n_splits=10, n_repeats=3, estado_aleatorio=1) # evaluar el modelo n_scores = cross_val_score(modelo, X, y, puntuación=‘precisión’, CV=CV, n_jobs=–1) # informe de rendimiento impresión(‘Precisión media:% .3f (% .3f)’ % (significar(n_scores), std(n_scores))) |
La ejecución del ejemplo informa la precisión de la desviación estándar y media del modelo.
Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o procedimiento de evaluación, o las diferencias en la precisión numérica. Considere ejecutar el ejemplo varias veces y compare el resultado promedio.
En este caso, podemos ver que el conjunto KNORA-E y los hiperparámetros predeterminados logran una precisión de clasificación de aproximadamente el 91,5 por ciento.
|
Precisión media: 0,915 (0,009) |
También podemos utilizar el conjunto KNORA-E como modelo final y hacer predicciones para la clasificación.
Primero, el modelo se ajusta a todos los datos disponibles, luego predecir() La función se puede llamar para hacer predicciones sobre nuevos datos.
El siguiente ejemplo demuestra esto en nuestro conjunto de datos de clasificación binaria.
|
# hacer una predicción con la selección de conjuntos dinámicos KNORA-E de sklearn.conjuntos de datos importar make_classification de deslib.des.knora_e importar KNORAE # definir conjunto de datos X, y = make_classification(n_samples=10000, n_features=20, n_informativo=15, n_redundante=5, estado_aleatorio=7) # definir el modelo modelo = KNORAE() # ajustar el modelo en todo el conjunto de datos modelo.encajar(X, y) # haz una sola predicción fila = [[0.2929949,–4.21223056,–1.288332,–2.17849815,–0,64527665,2.58097719,0.28422388,–7.1827928,–1.91211104,2.73729512,0.81395695,3.96973717,–2.66939799,3.34692332,4.19791821,0,99990998,–0,30201875,–4.43170633,–2.82646737,0,44916808] yhat = modelo.predecir([[fila]) impresión(‘Clase prevista:% d’ % yhat[[0]) |
La ejecución del ejemplo se ajusta al algoritmo de selección de conjuntos dinámicos KNORA-E en todo el conjunto de datos y luego se usa para hacer una predicción en una nueva fila de datos, como podríamos hacer al usar el modelo en una aplicación.
Ahora que estamos familiarizados con el uso de KNORA-E, veamos el método KNORA-Union.
KNORA-Unión (KNORA-U)
Podemos evaluar un modelo KNORA-Union en el conjunto de datos sintéticos.
En este caso, usaremos hiperparámetros de modelo predeterminados, incluidos árboles de decisión empaquetados como grupo de modelos de clasificador y un k = 7 para la selección del vecindario local al hacer una predicción.
Evaluaremos el modelo usando validación cruzada estratificada repetida de k-veces con tres repeticiones y 10 pliegues. Informaremos la desviación estándar y media de la precisión del modelo en todas las repeticiones y pliegues.
El ejemplo completo se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 |
# evaluar la selección dinámica de conjuntos dinámicos KNORA-U para clasificación binaria de numpy importar significar de numpy importar std de sklearn.conjuntos de datos importar make_classification de sklearn.model_selection importar cross_val_score de sklearn.model_selection importar Repetido Estratificado KFold de deslib.des.knora_u importar KNORAU # definir conjunto de datos X, y = make_classification(n_samples=10000, n_features=20, n_informativo=15, n_redundante=5, estado_aleatorio=7) # definir el modelo modelo = KNORAU() # definir el procedimiento de evaluación CV = Repetido Estratificado KFold(n_splits=10, n_repeats=3, estado_aleatorio=1) # evaluar el modelo n_scores = cross_val_score(modelo, X, y, puntuación=‘precisión’, CV=CV, n_jobs=–1) # informe de rendimiento impresión(‘Precisión media:% .3f (% .3f)’ % (significar(n_scores), std(n_scores))) |
La ejecución del ejemplo informa la precisión de la desviación estándar y media del modelo.
Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o procedimiento de evaluación, o las diferencias en la precisión numérica. Considere ejecutar el ejemplo varias veces y compare el resultado promedio.
En este caso, podemos ver que el modelo de selección de conjuntos dinámicos KNORA-U y los hiperparámetros predeterminados logran una precisión de clasificación de aproximadamente el 93,3 por ciento.
|
Precisión media: 0,933 (0,009) |
También podemos utilizar el modelo KNORA-U como modelo final y hacer predicciones para la clasificación.
Primero, el modelo se ajusta a todos los datos disponibles, luego predecir() La función se puede llamar para hacer predicciones sobre nuevos datos.
El siguiente ejemplo demuestra esto en nuestro conjunto de datos de clasificación binaria.
|
# hacer una predicción con la selección de conjuntos dinámicos KNORA-U de sklearn.conjuntos de datos importar make_classification de deslib.des.knora_u importar KNORAU # definir conjunto de datos X, y = make_classification(n_samples=10000, n_features=20, n_informativo=15, n_redundante=5, estado_aleatorio=7) # definir el modelo modelo = KNORAU() # ajustar el modelo en todo el conjunto de datos modelo.encajar(X, y) # haz una sola predicción fila = [[0.2929949,–4.21223056,–1.288332,–2.17849815,–0,64527665,2.58097719,0.28422388,–7.1827928,–1.91211104,2.73729512,0.81395695,3.96973717,–2.66939799,3.34692332,4.19791821,0,99990998,–0,30201875,–4.43170633,–2.82646737,0,44916808] yhat = modelo.predecir([[fila]) impresión(‘Clase prevista:% d’ % yhat[[0]) |
La ejecución del ejemplo se ajusta al modelo KNORA-U en todo el conjunto de datos y luego se usa para hacer una predicción en una nueva fila de datos, como podríamos hacer al usar el modelo en una aplicación.
Ahora que estamos familiarizados con el uso de la API scikit-learn para evaluar y usar modelos KNORA, veamos cómo configurar el modelo.
Ajuste de hiperparámetros para KNORA
En esta sección, analizaremos más de cerca algunos de los hiperparámetros que debería considerar ajustar para el modelo KNORA y su efecto en el rendimiento del modelo.
Hay muchos hiperparámetros que podemos mirar para KNORA, aunque en este caso, veremos el valor de k en el k-modelo vecino más cercano utilizado en la evaluación local de los modelos, y cómo utilizar un grupo personalizado de clasificadores.
Usaremos KNORA-Union como base para estos experimentos, aunque la elección del método específico es arbitraria.
Explore k en k-Vecinos más cercanos
La configuración del algoritmo de los k vecinos más cercanos es fundamental para el modelo KNORA, ya que define el alcance del vecindario en el que se considera cada conjunto para la selección.
El valor k controla el tamaño del vecindario y es importante establecerlo en un valor que sea apropiado para su conjunto de datos, específicamente la densidad de muestras en el espacio de características. Un valor demasiado pequeño significará que los ejemplos relevantes en el conjunto de entrenamiento podrían excluirse del vecindario, mientras que los valores demasiado grandes pueden significar que la señal está siendo eliminada por demasiados ejemplos.
El siguiente ejemplo de código explora la precisión de clasificación del algoritmo KNORA-U con valores k de 2 a 21.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
# explore k en knn para la selección de conjuntos dinámicos KNORA-U de numpy importar significar de numpy importar std de sklearn.conjuntos de datos importar make_classification de sklearn.model_selection importar cross_val_score de sklearn.model_selection importar Repetido Estratificado KFold de deslib.des.knora_u importar KNORAU de matplotlib importar pyplot # obtener el conjunto de datos def get_dataset(): X, y = make_classification(n_samples=10000, n_features=20, n_informativo=15, n_redundante=5, estado_aleatorio=7) regreso X, y # obtener una lista de modelos para evaluar def get_models(): modelos = dictar() por norte en distancia(2,22): modelos[[str(norte)] = KNORAU(k=norte) regreso modelos # evaluar un modelo dado mediante validación cruzada def evaluar_modelo(modelo): CV = Repetido Estratificado KFold(n_splits=10, n_repeats=3, estado_aleatorio=1) puntuaciones = cross_val_score(modelo, X, y, puntuación=‘precisión’, CV=CV, n_jobs=–1) regreso puntuaciones # definir conjunto de datos X, y = get_dataset() # obtener los modelos para evaluar modelos = get_models() # evaluar los modelos y almacenar los resultados resultados, nombres = lista(), lista() por nombre, modelo en modelos.artículos(): puntuaciones = evaluar_modelo(modelo) resultados.adjuntar(puntuaciones) nombres.adjuntar(nombre) impresión(‘>% s% .3f (% .3f)’ % (nombre, significar(puntuaciones), std(puntuaciones))) # trazar el rendimiento del modelo para comparar pyplot.diagrama de caja(resultados, etiquetas=nombres, mostrar significa=Cierto) pyplot.show() |
Ejecutar el ejemplo primero informa la precisión media para cada tamaño de vecindario configurado.
Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o procedimiento de evaluación, o las diferencias en la precisión numérica. Considere ejecutar el ejemplo varias veces y compare el resultado promedio.
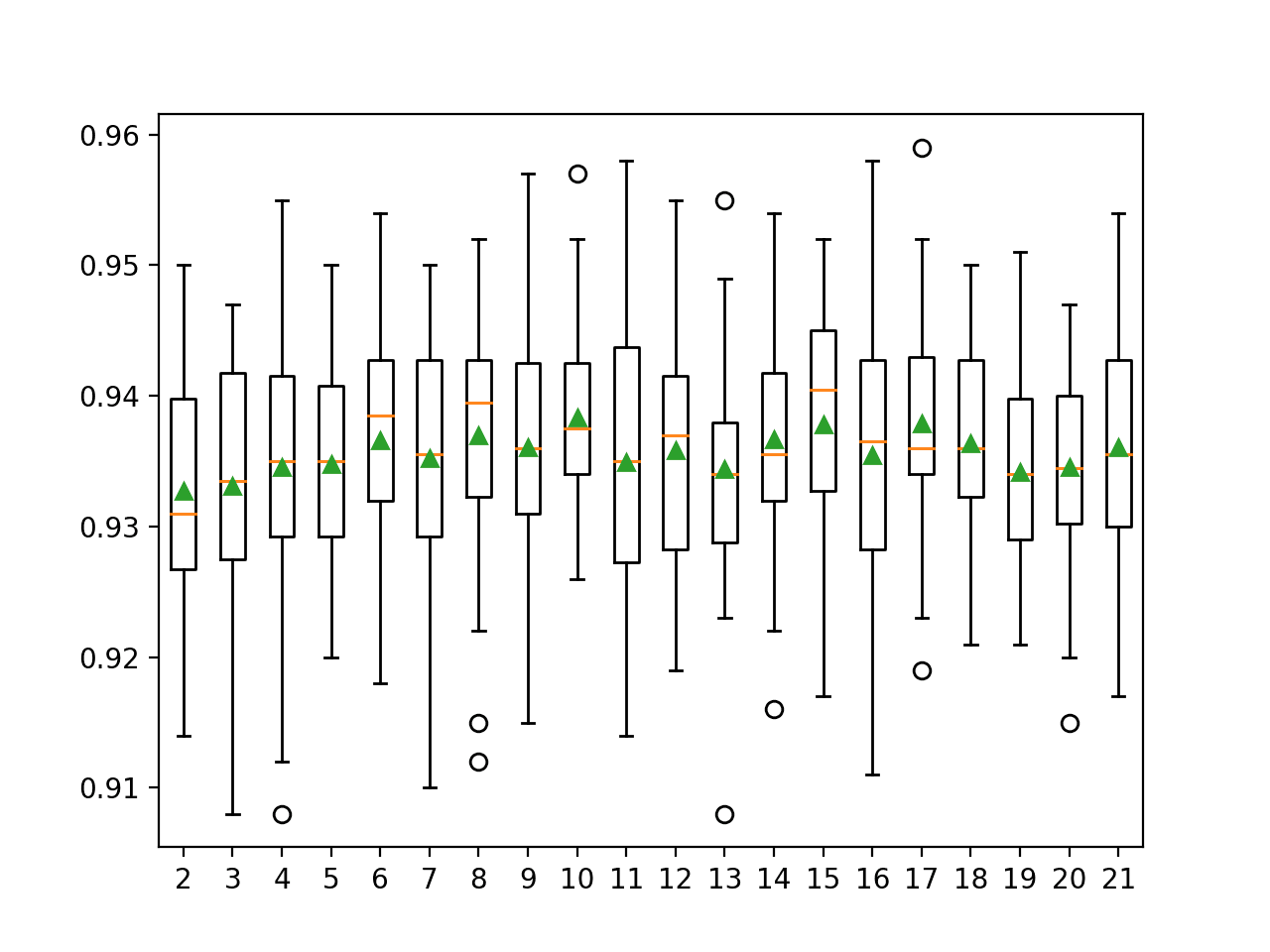
En este caso, podemos ver que la precisión aumenta con el tamaño del vecindario, quizás hasta k = 10, donde parece estabilizarse.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
>2 0.933 (0.008) >3 0.933 (0.010) >4 0.935 (0.011) >5 0.935 (0.007) >6 0.937 (0.009) >7 0.935 (0.011) >8 0.937 (0.010) >9 0.936 (0.009) >10 0.938 (0.007) >11 0.935 (0.010) >12 0.936 (0.009) >13 0.934 (0.009) >14 0.937 (0.009) >15 0.938 (0.009) >16 0.935 (0.010) >17 0.938 (0.008) >18 0.936 (0.007) >19 0.934 (0.007) >20 0.935 (0.007) >21 0.936 (0.009) |
A box and whisker plot is created for the distribution of accuracy scores for each configured neighborhood size.
We can see the general trend of increasing model performance and k value before reaching a plateau.

Box and Whisker Plots of Accuracy Distributions for k Values in KNORA-U
Explore Algorithms for Classifier Pool
The choice of algorithms used in the pool for the KNORA is another important hyperparameter.
By default, bagged decision trees are used, as it has proven to be an effective approach on a range of classification tasks. Nevertheless, a custom pool of classifiers can be considered.
In the majority of DS publications, the pool of classifiers is generated using either well known ensemble generation methods such as Bagging, or by using heterogeneous classifiers.
— Dynamic Classifier Selection: Recent Advances And Perspectives, 2018.
This requires first defining a list of classifier models to use and fitting each on the training dataset. Unfortunately, this means that the automatic k-fold cross-validation model evaluation methods in scikit-learn cannot be used in this case. Instead, we will use a train-test split so that we can fit the classifier pool manually on the training dataset.
The list of fit classifiers can then be specified to the KNORA-Union (or KNORA-Eliminate) class via the “pool_classifiers” argument. In this case, we will use a pool that includes logistic regression, a decision tree, and a naive Bayes classifier.
The complete example of evaluating the KNORA ensemble and a custom set of classifiers on the synthetic dataset is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
# evaluate KNORA-U dynamic ensemble selection with a custom pool of algorithms de sklearn.datasets import make_classification de sklearn.model_selection import train_test_split de sklearn.metrics import accuracy_score de deslib.des.knora_u import KNORAU de sklearn.linear_model import LogisticRegression de sklearn.árbol import DecisionTreeClassifier de sklearn.naive_bayes import GaussianNB X, y = make_classification(n_samples=10000, n_features=20, n_informative=15, n_redundant=5, random_state=7) # split the dataset into train and test sets X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5, random_state=1) # define classifiers to use in the pool classifiers = [[ LogisticRegression(), DecisionTreeClassifier(), GaussianNB()] # fit each classifier on the training set for C en classifiers: C.fit(X_train, y_train) # define the KNORA-U model model = KNORAU(pool_classifiers=classifiers) # fit the model model.fit(X_train, y_train) # make predictions on the test set yhat = model.predict(X_test) # evaluate predictions score = accuracy_score(y_test, yhat) print(‘Accuracy: %.3f’ % (score)) |
Running the example first reports the mean accuracy for the model with the custom pool of classifiers.
Nota: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, we can see that the model achieved an accuracy of about 91.3 percent.
In order to adopt the KNORA model, it must perform better than any contributing model. Otherwise, we would simply use the contributing model that performs better.
We can check this by evaluating the performance of each contributing classifier on the test set.
|
... # evaluate contributing models for C en classifiers: yhat = C.predict(X_test) score = accuracy_score(y_test, yhat) print(‘>%s: %.3f’ % (C.__class__.__name__, score)) |
The updated example of KNORA with a custom pool of classifiers that are also evaluated independently is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
# evaluate KNORA-U dynamic ensemble selection with a custom pool of algorithms de sklearn.datasets import make_classification de sklearn.model_selection import train_test_split de sklearn.metrics import accuracy_score de deslib.des.knora_u import KNORAU de sklearn.linear_model import LogisticRegression de sklearn.árbol import DecisionTreeClassifier de sklearn.naive_bayes import GaussianNB X, y = make_classification(n_samples=10000, n_features=20, n_informative=15, n_redundant=5, random_state=7) # split the dataset into train and test sets X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5, random_state=1) # define classifiers to use in the pool classifiers = [[ LogisticRegression(), DecisionTreeClassifier(), GaussianNB()] # fit each classifier on the training set for C en classifiers: C.fit(X_train, y_train) # define the KNORA-U model model = KNORAU(pool_classifiers=classifiers) # fit the model model.fit(X_train, y_train) # make predictions on the test set yhat = model.predict(X_test) # evaluate predictions score = accuracy_score(y_test, yhat) print(‘Accuracy: %.3f’ % (score)) # evaluate contributing models for C en classifiers: yhat = C.predict(X_test) score = accuracy_score(y_test, yhat) print(‘>%s: %.3f’ % (C.__class__.__name__, score)) |
Running the example first reports the mean accuracy for the model with the custom pool of classifiers and the accuracy of each contributing model.
Nota: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, we can see that again the KNORAU achieves an accuracy of about 91.3 percent, which is better than any contributing model.
|
Accuracy: 0.913 >LogisticRegression: 0.878 >DecisionTreeClassifier: 0.885 >GaussianNB: 0.873 |
Instead of specifying a pool of classifiers, it is also possible to specify a single ensemble algorithm from the scikit-learn library and the KNORA algorithm will automatically use the internal ensemble members as classifiers.
For example, we can use a random forest ensemble with 1,000 members as the base classifiers to consider within KNORA as follows:
|
... # define classifiers to use in the pool pool = RandomForestClassifier(n_estimators=1000) # fit the classifiers on the training set pool.fit(X_train, y_train) # define the KNORA-U model model = KNORAU(pool_classifiers=pool) |
Tying this together, the complete example of KNORA-U with random forest ensemble members as classifiers is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
# evaluate KNORA-U with a random forest ensemble as the classifier pool de sklearn.datasets import make_classification de sklearn.model_selection import train_test_split de sklearn.metrics import accuracy_score de deslib.des.knora_u import KNORAU de sklearn.ensemble import RandomForestClassifier X, y = make_classification(n_samples=10000, n_features=20, n_informative=15, n_redundant=5, random_state=7) # split the dataset into train and test sets X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5, random_state=1) # define classifiers to use in the pool pool = RandomForestClassifier(n_estimators=1000) # fit the classifiers on the training set pool.fit(X_train, y_train) # define the KNORA-U model model = KNORAU(pool_classifiers=pool) # fit the model model.fit(X_train, y_train) # make predictions on the test set yhat = model.predict(X_test) # evaluate predictions score = accuracy_score(y_test, yhat) print(‘Accuracy: %.3f’ % (score)) # evaluate the standalone model yhat = pool.predict(X_test) score = accuracy_score(y_test, yhat) print(‘>%s: %.3f’ % (pool.__class__.__name__, score)) |
Running the example first reports the mean accuracy for the model with the custom pool of classifiers and the accuracy of the random forest model.
Nota: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, we can see that the KNORA model with dynamically selected ensemble members out-performs the random forest with the statically selected (full set) ensemble members.
|
Accuracy: 0.968 >RandomForestClassifier: 0.967 |
Further Reading
This section provides more resources on the topic if you are looking to go deeper.
Related Tutorials
Papers
Books
APIs
Summary
In this tutorial, you discovered how to develop dynamic ensemble selection models in Python.
Specifically, you learned:
- Dynamic ensemble selection algorithms automatically choose ensemble members when making a prediction on new data.
- How to develop and evaluate dynamic ensemble selection models for classification tasks using the scikit-learn API.
- How to explore the effect of dynamic ensemble selection model hyperparameters on classification accuracy.
Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.

