La regresión es una tarea de modelización que implica la predicción de un valor numérico dado una entrada.
Los algoritmos utilizados para las tareas de regresión también se denominan «regresión«…con los algoritmos más conocidos y tal vez más exitosos de regresión lineal.
La regresión lineal se ajusta a una línea o hiperplano que describe mejor la relación lineal entre las entradas y el valor numérico objetivo. Si los datos contienen valores atípicos, la línea puede resultar sesgada, lo que resulta en un peor rendimiento predictivo. Una regresión robusta se refiere a un conjunto de algoritmos que son robustos en presencia de valores atípicos en los datos de capacitación.
En este tutorial, descubrirá robustos algoritmos de regresión para el aprendizaje automático.
Después de completar este tutorial, lo sabrás:
- Se pueden utilizar robustos algoritmos de regresión para los datos con valores atípicos en los valores de entrada o de destino.
- Cómo evaluar algoritmos de regresión robustos para una tarea de modelado predictivo de regresión.
- Cómo comparar algoritmos de regresión robustos usando su línea de mejor ajuste en el conjunto de datos.
Empecemos.

Robusta regresión para el aprendizaje de la máquina en Python
Foto de Lenny K Photography, algunos derechos reservados.
Resumen del Tutorial
Este tutorial está dividido en cuatro partes; son:
- Regresión con valores atípicos
- Conjunto de datos de regresión con valores atípicos
- Robustos algoritmos de regresión
- Comparar los robustos algoritmos de regresión
Regresión con valores atípicos
El modelado predictivo de regresión implica la predicción de una variable numérica dada alguna entrada, a menudo numérica.
Los algoritmos de aprendizaje automático utilizados para las tareas de modelado predictivo de regresión también se denominan «regresión«o»algoritmos de regresión.” El método más común es la regresión lineal.
Muchos algoritmos de regresión son lineales en el sentido de que asumen que la relación entre la variable o variables de entrada y la variable objetivo es lineal, como una línea en dos dimensiones, un plano en tres dimensiones y un hiperplano en dimensiones superiores. Esta es una suposición razonable para muchas tareas de predicción.
La regresión lineal supone que la distribución de probabilidad de cada variable se comporta bien, como tiene una distribución gaussiana. Cuanto menos bien se comporte la distribución de probabilidad de una característica en un conjunto de datos, menos probable será que la regresión lineal encuentre un buen ajuste.
Un problema específico de la distribución de probabilidad de las variables cuando se utiliza la regresión lineal son los valores atípicos. Se trata de observaciones que están muy lejos de la distribución esperada. Por ejemplo, si una variable tiene una distribución gaussiana, entonces una observación que tiene 3 ó 4 (o más) desviaciones estándar de la media se considera un valor atípico.
Un conjunto de datos puede tener valores atípicos en las variables de entrada o en la variable objetivo, y ambas pueden causar problemas para un algoritmo de regresión lineal.
Los valores atípicos de un conjunto de datos pueden sesgar las estadísticas resumidas calculadas para la variable, como la media y la desviación estándar, lo que a su vez puede sesgar el modelo hacia los valores atípicos, alejándolo de la masa central de observaciones. Esto da lugar a modelos que tratan de equilibrar el buen desempeño en los datos atípicos y los datos normales, y el peor desempeño en ambos en general.
La solución, en cambio, es utilizar versiones modificadas de la regresión lineal que aborden específicamente la expectativa de valores atípicos en el conjunto de datos. Estos métodos se conocen como algoritmos de regresión robusta.
Conjunto de datos de regresión con valores atípicos
Podemos definir un conjunto de datos de regresión sintética usando la función make_regression().
En este caso, queremos un conjunto de datos que podamos trazar y entender fácilmente. Esto puede lograrse utilizando una sola variable de entrada y una sola variable de salida. No queremos que la tarea sea demasiado fácil, así que añadiremos una gran cantidad de ruido estadístico.
|
... X, y = make_regression(n_muestras=100, n_funciones=1, fuerza_de_cola=0.9, effective_rank=1, n_informativo=1, ruido=3, sesgo=50, estado_aleatorio=1) |
Una vez que tengamos el conjunto de datos, podemos aumentarlo añadiendo valores atípicos. Específicamente, añadiremos valores atípicos a las variables de entrada.
Esto puede hacerse cambiando algunas de las variables de entrada para que tengan un valor que sea un factor del número de desviaciones estándar alejado de la media, como por ejemplo de 2 a 4. Añadiremos 10 valores atípicos al conjunto de datos.
|
# Agregar algunos valores atípicos artificiales semilla(1) para i en rango(10): factor = randint(2, 4) si al azar() > 0.5: X[[i] += factor * X.std() más: X[[i] -= factor * X.std() |
Podemos unir esto en una función que preparará el conjunto de datos. Esta función puede entonces ser llamada y podemos trazar el conjunto de datos con los valores de entrada en el eje x y el objetivo o resultado en el eje y.
El ejemplo completo de la preparación y el trazado del conjunto de datos se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
# Crear un conjunto de datos de regresión con valores atípicos de al azar importación al azar de al azar importación randint de al azar importación semilla de sklearn.conjuntos de datos importación make_regression de matplotlib importación pyplot # Prepara el conjunto de datos def get_dataset(): X, y = make_regression(n_muestras=100, n_funciones=1, fuerza_de_cola=0.9, effective_rank=1, n_informativo=1, ruido=3, sesgo=50, estado_aleatorio=1) # Agregar algunos valores atípicos artificiales semilla(1) para i en rango(10): factor = randint(2, 4) si al azar() > 0.5: X[[i] += factor * X.std() más: X[[i] -= factor * X.std() volver X, y # Cargar conjunto de datos X, y = get_dataset() # Resumir la forma imprimir(X.forma, y.forma) # Gráfica de dispersión de entrada contra salida pyplot.Dispersión(X, y) pyplot.mostrar() |
Ejecutando el ejemplo se crea el conjunto de datos de regresión sintética y se añaden valores atípicos.
A continuación se traza el conjunto de datos, y podemos ver claramente la relación lineal en los datos, con el ruido estadístico, y un modesto número de valores atípicos como puntos alejados de la masa principal de datos.
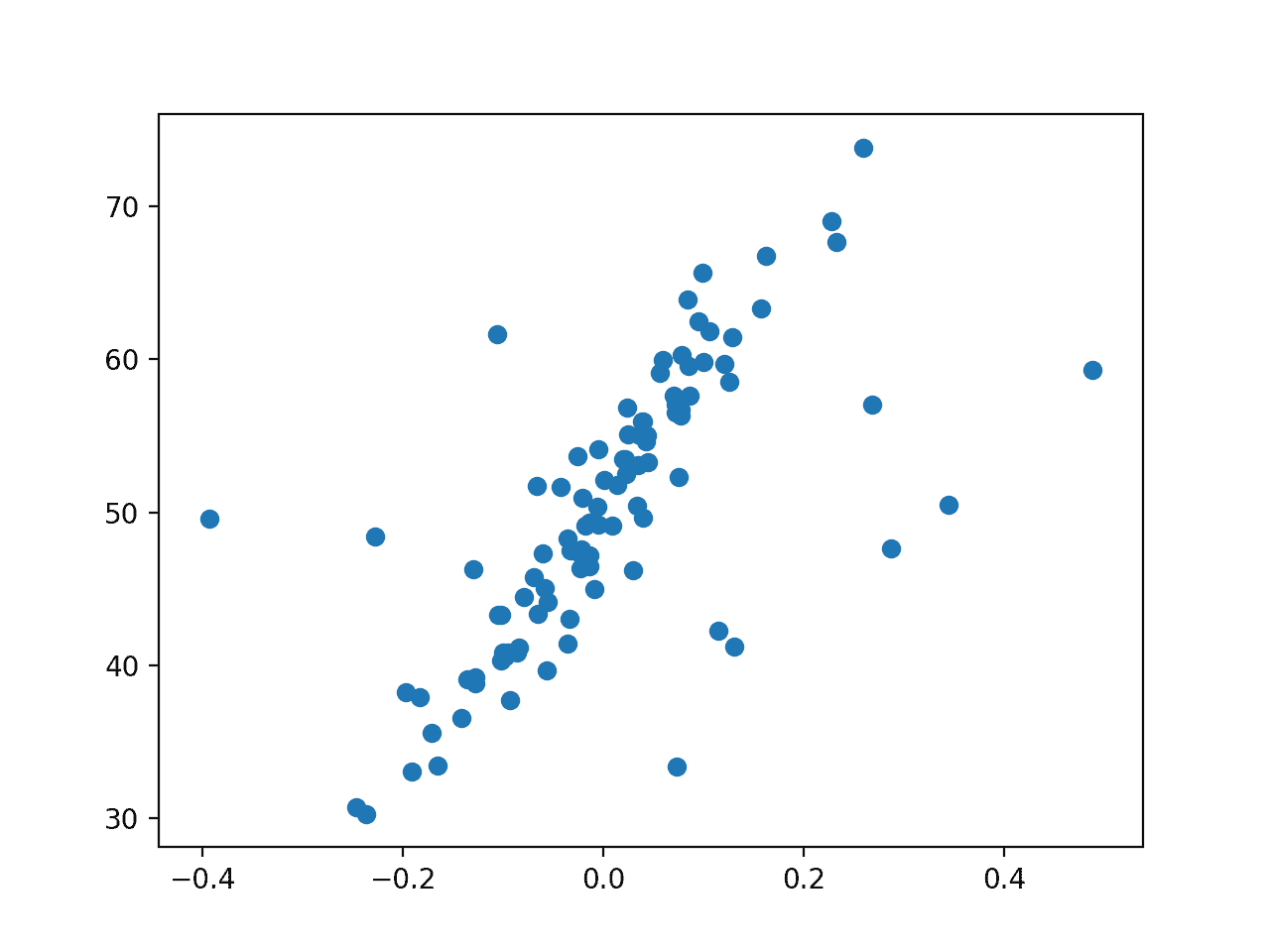
Diagrama de dispersión del conjunto de datos de regresión con valores atípicos
Ahora que tenemos un conjunto de datos, vamos a ajustar diferentes modelos de regresión en él.
Robustos algoritmos de regresión
En esta sección, consideraremos diferentes algoritmos robustos de regresión para el conjunto de datos.
Regresión lineal (no es robusta)
Antes de sumergirnos en robustos algoritmos de regresión, empecemos con la regresión lineal.
Podemos evaluar la regresión lineal usando la validación cruzada repetida de k en el conjunto de datos de la regresión con valores atípicos. Mediremos el error medio absoluto y esto proporcionará un límite inferior en el rendimiento del modelo en esta tarea que podríamos esperar que algunos algoritmos de regresión robustos superen.
|
# Evaluar un modelo def evaluate_model(X, y, modelo): # Definir el método de evaluación del modelo cv = RepetidoKFold(n_splits=10, n_repeticiones=3, estado_aleatorio=1) # Evaluar el modelo resultados = puntaje_valor_cruzado(modelo, X, y, puntuación=‘neg_mean_absolute_error’, cv=cv, n_jobs=–1) # forzar las puntuaciones a ser positivas volver absoluto(resultados) |
También podemos trazar la línea del modelo que mejor se ajuste al conjunto de datos. Para ello, primero ajustamos el modelo en todo el conjunto de datos de entrenamiento, luego creamos un conjunto de datos de entrada que es una cuadrícula a través de todo el dominio de entrada, hacemos una predicción para cada uno, y luego dibujamos una línea para las entradas y salidas predichas.
Esta trama muestra cómo el modelo «ve» el problema, específicamente la relación entre las variables de entrada y salida. La idea es que la línea será sesgada por los valores atípicos al usar la regresión lineal.
|
# Traza el conjunto de datos y la línea de mejor ajuste del modelo def plot_best_fit(X, y, modelo): # fut el modelo en todos los datos modelo.encajar(X, y) # Trazar el conjunto de datos pyplot.Dispersión(X, y) # trazar la línea de mejor ajuste xaxis = arange(X.min(), X.max(), 0.01) yaxis = modelo.predecir(xaxis.remodelar((len(xaxis), 1))) pyplot.parcela(xaxis, yaxis, color=‘r’) # mostrar la trama pyplot.título(escriba(modelo).__nombre__) pyplot.mostrar() |
Enlazando todo esto, el ejemplo completo de regresión lineal se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 |
# Regresión lineal en un conjunto de datos con valores atípicos de al azar importación al azar de al azar importación randint de al azar importación semilla de numpy importación arange de numpy importación significa de numpy importación std de numpy importación absoluto de sklearn.conjuntos de datos importación make_regression de sklearn.modelo_lineal importación LinearRegression de sklearn.model_selection importación puntaje_valor_cruzado de sklearn.model_selection importación RepetidoKFold de matplotlib importación pyplot # Prepara el conjunto de datos def get_dataset(): X, y = make_regression(n_muestras=100, n_funciones=1, fuerza_de_cola=0.9, effective_rank=1, n_informativo=1, ruido=3, sesgo=50, estado_aleatorio=1) # Agregar algunos valores atípicos artificiales semilla(1) para i en rango(10): factor = randint(2, 4) si al azar() > 0.5: X[[i] += factor * X.std() más: X[[i] -= factor * X.std() volver X, y # Evaluar un modelo def evaluate_model(X, y, modelo): # Definir el método de evaluación del modelo cv = RepetidoKFold(n_splits=10, n_repeticiones=3, estado_aleatorio=1) # Evaluar el modelo resultados = puntaje_valor_cruzado(modelo, X, y, puntuación=‘neg_mean_absolute_error’, cv=cv, n_jobs=–1) # forzar las puntuaciones a ser positivas volver absoluto(resultados) # Traza el conjunto de datos y la línea de mejor ajuste del modelo def plot_best_fit(X, y, modelo): # fut el modelo en todos los datos modelo.encajar(X, y) # Trazar el conjunto de datos pyplot.Dispersión(X, y) # trazar la línea de mejor ajuste xaxis = arange(X.min(), X.max(), 0.01) yaxis = modelo.predecir(xaxis.remodelar((len(xaxis), 1))) pyplot.parcela(xaxis, yaxis, color=‘r’) # mostrar la trama pyplot.título(escriba(modelo).__nombre__) pyplot.mostrar() # Cargar conjunto de datos X, y = get_dataset() # Definir el modelo modelo = LinearRegression() # Evaluar el modelo resultados = evaluate_model(X, y, modelo) imprimir(«Promedio MAE: %.3f (%.3f) % (significa(resultados), std(resultados))) # trazar la línea de mejor ajuste plot_best_fit(X, y, modelo) |
Ejecutando el ejemplo primero reporta el promedio de MAE para el modelo en el conjunto de datos.
Podemos ver que la regresión lineal logra un MAE de alrededor de 5,2 en este conjunto de datos, proporcionando un límite superior en el error.
A continuación, el conjunto de datos se traza como un gráfico de dispersión que muestra los valores atípicos y se superpone con la línea de mejor ajuste del algoritmo de regresión lineal.
En este caso, podemos ver que la línea de mejor ajuste no está alineada con los datos y ha sido sesgada por los valores atípicos. A su vez, esperamos que esto haya causado que el modelo tenga un rendimiento peor de lo esperado en el conjunto de datos.
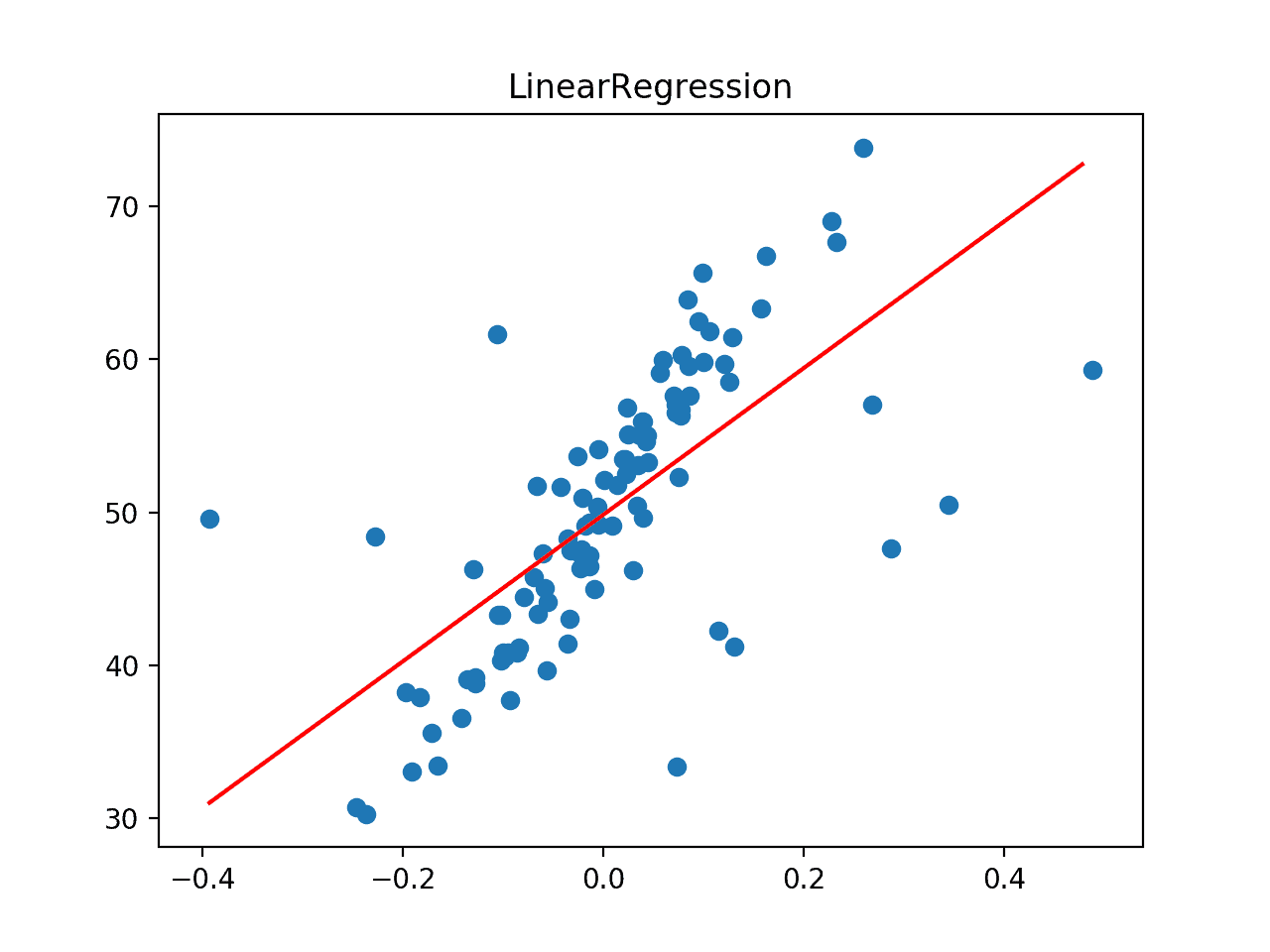
La línea de mejor ajuste para la regresión lineal en un conjunto de datos con valores atípicos
Regresión de Huber
La regresión de Huber es un tipo de regresión robusta que es consciente de la posibilidad de que existan valores atípicos en un conjunto de datos y les asigna menos peso que a otros ejemplos en el conjunto de datos.
Podemos usar la regresión de Huber a través de la clase de Huber-Regressor en el scikit-learn. El «epsilonEl argumento de «la diferencia» controla lo que se considera un valor atípico, donde los valores más pequeños consideran más los datos atípicos y, a su vez, hacen que el modelo sea más robusto para los valores atípicos. El valor por defecto es 1,35.
El siguiente ejemplo evalúa la regresión de Huber en el conjunto de datos de la regresión con valores atípicos, evaluando primero el modelo con validación cruzada repetida y luego trazando la línea de mejor ajuste.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 |
# Regresión de Huber en un conjunto de datos con valores atípicos de al azar importación al azar de al azar importación randint de al azar importación semilla de numpy importación arange de numpy importación significa de numpy importación std de numpy importación absoluto de sklearn.conjuntos de datos importación make_regression de sklearn.modelo_lineal importación HuberRegressor de sklearn.model_selection importación puntaje_valor_cruzado de sklearn.model_selection importación RepetidoKFold de matplotlib importación pyplot # Prepara el conjunto de datos def get_dataset(): X, y = make_regression(n_muestras=100, n_funciones=1, fuerza_de_cola=0.9, effective_rank=1, n_informativo=1, ruido=3, sesgo=50, estado_aleatorio=1) # Agregar algunos valores atípicos artificiales semilla(1) para i en rango(10): factor = randint(2, 4) si al azar() > 0.5: X[[i] += factor * X.std() más: X[[i] -= factor * X.std() volver X, y # Evaluar un modelo def evaluate_model(X, y, modelo): # Definir el método de evaluación del modelo cv = RepetidoKFold(n_splits=10, n_repeticiones=3, estado_aleatorio=1) # Evaluar el modelo resultados = puntaje_valor_cruzado(modelo, X, y, puntuación=‘neg_mean_absolute_error’, cv=cv, n_jobs=–1) # forzar las puntuaciones a ser positivas volver absoluto(resultados) # Traza el conjunto de datos y la línea de mejor ajuste del modelo def plot_best_fit(X, y, modelo): # fut el modelo en todos los datos modelo.encajar(X, y) # Trazar el conjunto de datos pyplot.Dispersión(X, y) # trazar la línea de mejor ajuste xaxis = arange(X.min(), X.max(), 0.01) yaxis = modelo.predecir(xaxis.remodelar((len(xaxis), 1))) pyplot.parcela(xaxis, yaxis, color=‘r’) # mostrar la trama pyplot.título(escriba(modelo).__nombre__) pyplot.mostrar() # Cargar conjunto de datos X, y = get_dataset() # Definir el modelo modelo = HuberRegressor() # Evaluar el modelo resultados = evaluate_model(X, y, modelo) imprimir(«Promedio MAE: %.3f (%.3f) % (significa(resultados), std(resultados))) # trazar la línea de mejor ajuste plot_best_fit(X, y, modelo) |
Ejecutando el ejemplo primero reporta el promedio de MAE para el modelo en el conjunto de datos.
Podemos ver que la regresión de Huber logra un MAE de alrededor de 4.435 en este conjunto de datos, superando el modelo de regresión lineal de la sección anterior.
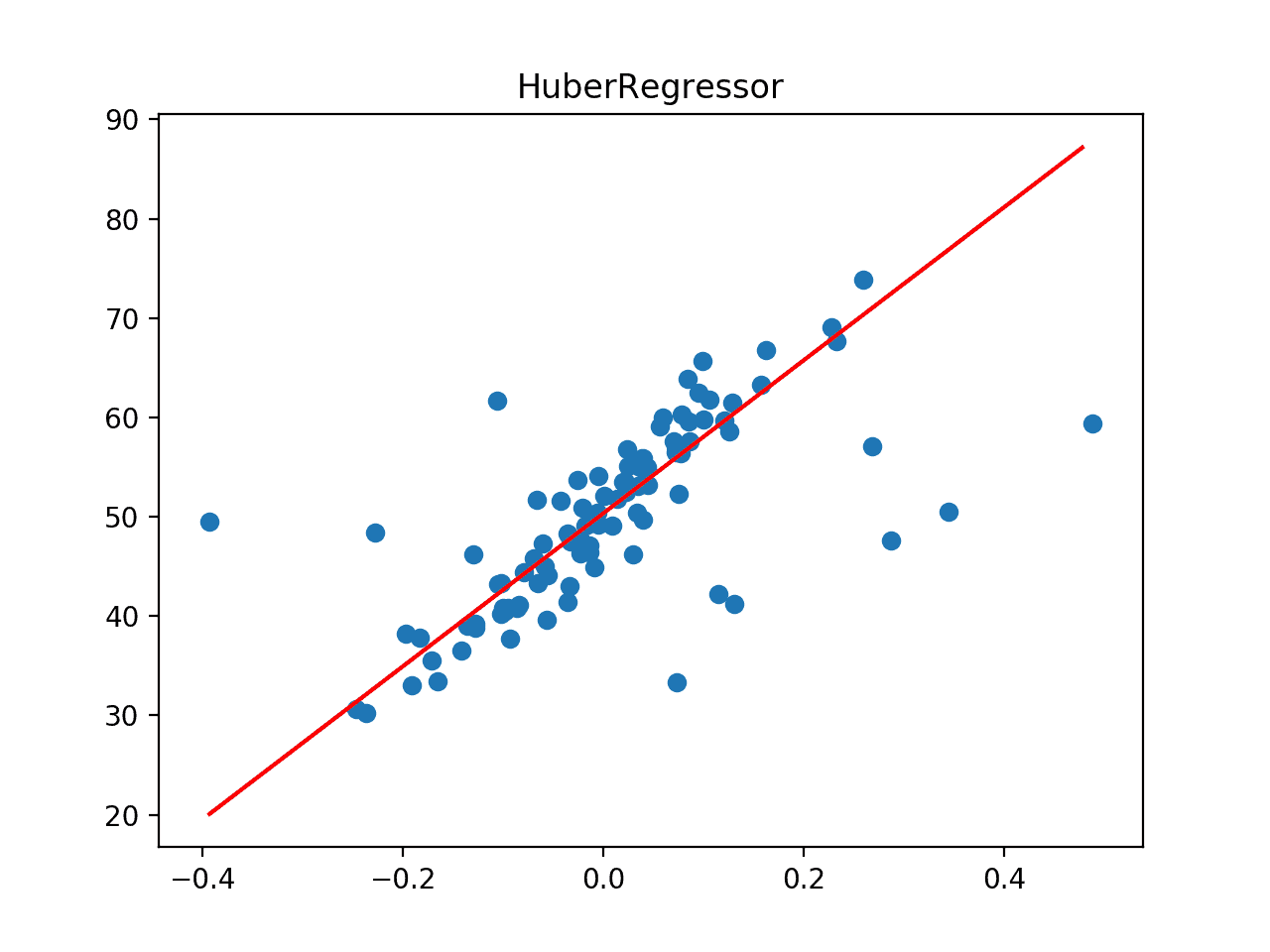
A continuación, el conjunto de datos se traza como un gráfico de dispersión que muestra los valores atípicos y se superpone con la línea de mejor ajuste del algoritmo.
En este caso, podemos ver que la línea de mejor ajuste está mejor alineada con el cuerpo principal de los datos, y no parece estar obviamente influenciada por los valores atípicos que están presentes.

La línea de mejor ajuste para la regresión de Huber en un conjunto de datos con valores atípicos
Regresión de RANSAC
El Consenso de Muestras Aleatorias, o RANSAC para abreviar, es otro robusto algoritmo de regresión.
RANSAC intenta separar los datos en valores atípicos e interiores y ajusta el modelo en los valores atípicos.
La biblioteca de aprendizaje de ciencias proporciona una implementación a través de la clase RANSACRegressor.
El siguiente ejemplo evalúa la regresión de RANSAC en el conjunto de datos de la regresión con valores atípicos, evaluando primero el modelo con validación cruzada repetida y luego trazando la línea de mejor ajuste.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 |
# Regresión de rescate en un conjunto de datos con valores atípicos de al azar importación al azar de al azar importación randint de al azar importación semilla de numpy importación arange de numpy importación significa de numpy importación std de numpy importación absoluto de sklearn.conjuntos de datos importación make_regression de sklearn.modelo_lineal importación RANSACRegressor de sklearn.model_selection importación puntaje_valor_cruzado de sklearn.model_selection importación RepetidoKFold de matplotlib importación pyplot # Prepara el conjunto de datos def get_dataset(): X, y = make_regression(n_muestras=100, n_funciones=1, fuerza_de_cola=0.9, effective_rank=1, n_informativo=1, ruido=3, sesgo=50, estado_aleatorio=1) # Agregar algunos valores atípicos artificiales semilla(1) para i en rango(10): factor = randint(2, 4) si al azar() > 0.5: X[[i] += factor * X.std() más: X[[i] -= factor * X.std() volver X, y # Evaluar un modelo def evaluate_model(X, y, modelo): # Definir el método de evaluación del modelo cv = RepetidoKFold(n_splits=10, n_repeticiones=3, estado_aleatorio=1) # Evaluar el modelo resultados = puntaje_valor_cruzado(modelo, X, y, puntuación=‘neg_mean_absolute_error’, cv=cv, n_jobs=–1) # forzar las puntuaciones a ser positivas volver absoluto(resultados) # Traza el conjunto de datos y la línea de mejor ajuste del modelo def plot_best_fit(X, y, modelo): # fut el modelo en todos los datos modelo.encajar(X, y) # Trazar el conjunto de datos pyplot.Dispersión(X, y) # trazar la línea de mejor ajuste xaxis = arange(X.min(), X.max(), 0.01) yaxis = modelo.predecir(xaxis.remodelar((len(xaxis), 1))) pyplot.parcela(xaxis, yaxis, color=‘r’) # mostrar la trama pyplot.título(escriba(modelo).__nombre__) pyplot.mostrar() # Cargar conjunto de datos X, y = get_dataset() # Definir el modelo modelo = RANSACRegressor() # Evaluar el modelo resultados = evaluate_model(X, y, modelo) imprimir(«Promedio MAE: %.3f (%.3f) % (significa(resultados), std(resultados))) # trazar la línea de mejor ajuste plot_best_fit(X, y, modelo) |
Ejecutando el ejemplo primero reporta el promedio de MAE para el modelo en el conjunto de datos.
Podemos ver que la regresión de RANSAC logra un MAE de alrededor de 4.454 en este conjunto de datos, superando el modelo de regresión lineal pero quizás no la regresión de Huber.
A continuación, el conjunto de datos se traza como un gráfico de dispersión que muestra los valores atípicos, y esto se superpone con la línea de mejor ajuste del algoritmo.
En este caso, podemos ver que la línea de mejor ajuste está alineada con el cuerpo principal de los datos, tal vez incluso mejor que la gráfica de la regresión de Huber.
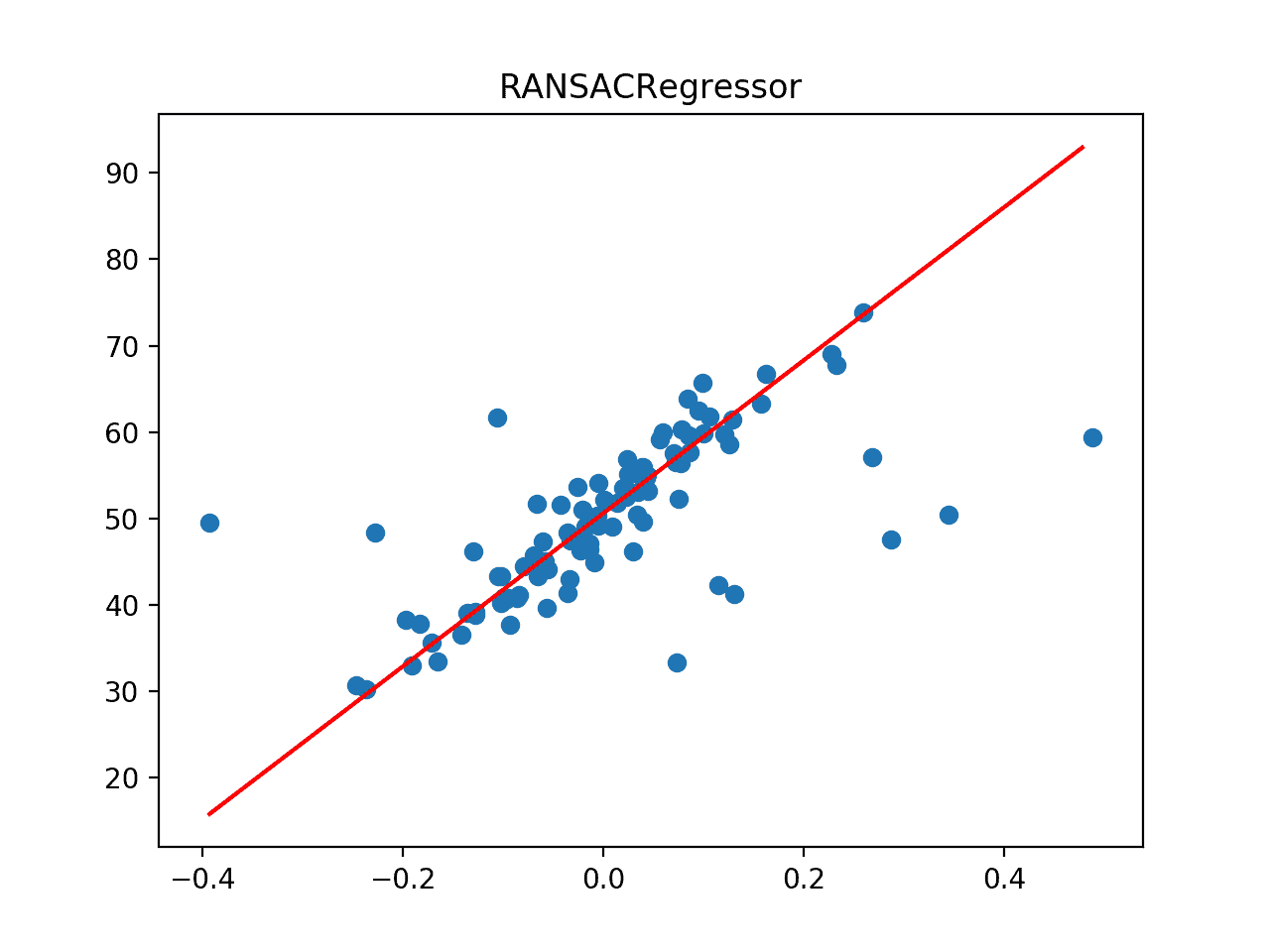
La línea de mejor ajuste para la regresión de RANSAC en un conjunto de datos con valores atípicos
La regresión de Theil Sen
La regresión de Theil Sen implica el ajuste de múltiples modelos de regresión en subconjuntos de los datos de entrenamiento y la combinación de los coeficientes al final.
El scikit-learn proporciona una implementación a través de la clase TheilSenRegressor.
El siguiente ejemplo evalúa la regresión de Theil Sen en el conjunto de datos de la regresión con valores atípicos, evaluando primero el modelo con validación cruzada repetida y luego trazando la línea de mejor ajuste.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 |
# Regresión de Theilsen en un conjunto de datos con valores atípicos de al azar importación al azar de al azar importación randint de al azar importación semilla de numpy importación arange de numpy importación significa de numpy importación std de numpy importación absoluto de sklearn.conjuntos de datos importación make_regression de sklearn.modelo_lineal importación TheilSenRegressor de sklearn.model_selection importación puntaje_valor_cruzado de sklearn.model_selection importación RepetidoKFold de matplotlib importación pyplot # Prepara el conjunto de datos def get_dataset(): X, y = make_regression(n_muestras=100, n_funciones=1, fuerza_de_cola=0.9, effective_rank=1, n_informativo=1, ruido=3, sesgo=50, estado_aleatorio=1) # Agregar algunos valores atípicos artificiales semilla(1) para i en rango(10): factor = randint(2, 4) si al azar() > 0.5: X[[i] += factor * X.std() más: X[[i] -= factor * X.std() volver X, y # Evaluar un modelo def evaluate_model(X, y, modelo): # Definir el método de evaluación del modelo cv = RepetidoKFold(n_splits=10, n_repeticiones=3, estado_aleatorio=1) # Evaluar el modelo resultados = puntaje_valor_cruzado(modelo, X, y, puntuación=‘neg_mean_absolute_error’, cv=cv, n_jobs=–1) # forzar las puntuaciones a ser positivas volver absoluto(resultados) # Traza el conjunto de datos y la línea de mejor ajuste del modelo def plot_best_fit(X, y, modelo): # fut el modelo en todos los datos modelo.encajar(X, y) # Trazar el conjunto de datos pyplot.Dispersión(X, y) # trazar la línea de mejor ajuste xaxis = arange(X.min(), X.max(), 0.01) yaxis = modelo.predecir(xaxis.remodelar((len(xaxis), 1))) pyplot.parcela(xaxis, yaxis, color=‘r’) # mostrar la trama pyplot.título(escriba(modelo).__nombre__) pyplot.mostrar() # Cargar conjunto de datos X, y = get_dataset() # Definir el modelo modelo = TheilSenRegressor() # Evaluar el modelo resultados = evaluate_model(X, y, modelo) imprimir(«Promedio MAE: %.3f (%.3f) % (significa(resultados), std(resultados))) # trazar la línea de mejor ajuste plot_best_fit(X, y, modelo) |
Ejecutando el ejemplo primero reporta el promedio de MAE para el modelo en el conjunto de datos.
Podemos ver que la regresión de Theil Sen logra un MAE de alrededor de 4.371 en este conjunto de datos, superando el modelo de regresión lineal así como la regresión de RANSAC y Huber.
A continuación, el conjunto de datos se traza como un gráfico de dispersión que muestra los valores atípicos, y esto se superpone con la línea de mejor ajuste del algoritmo.
En este caso, podemos ver que la línea de mejor ajuste está alineada con el cuerpo principal de los datos.
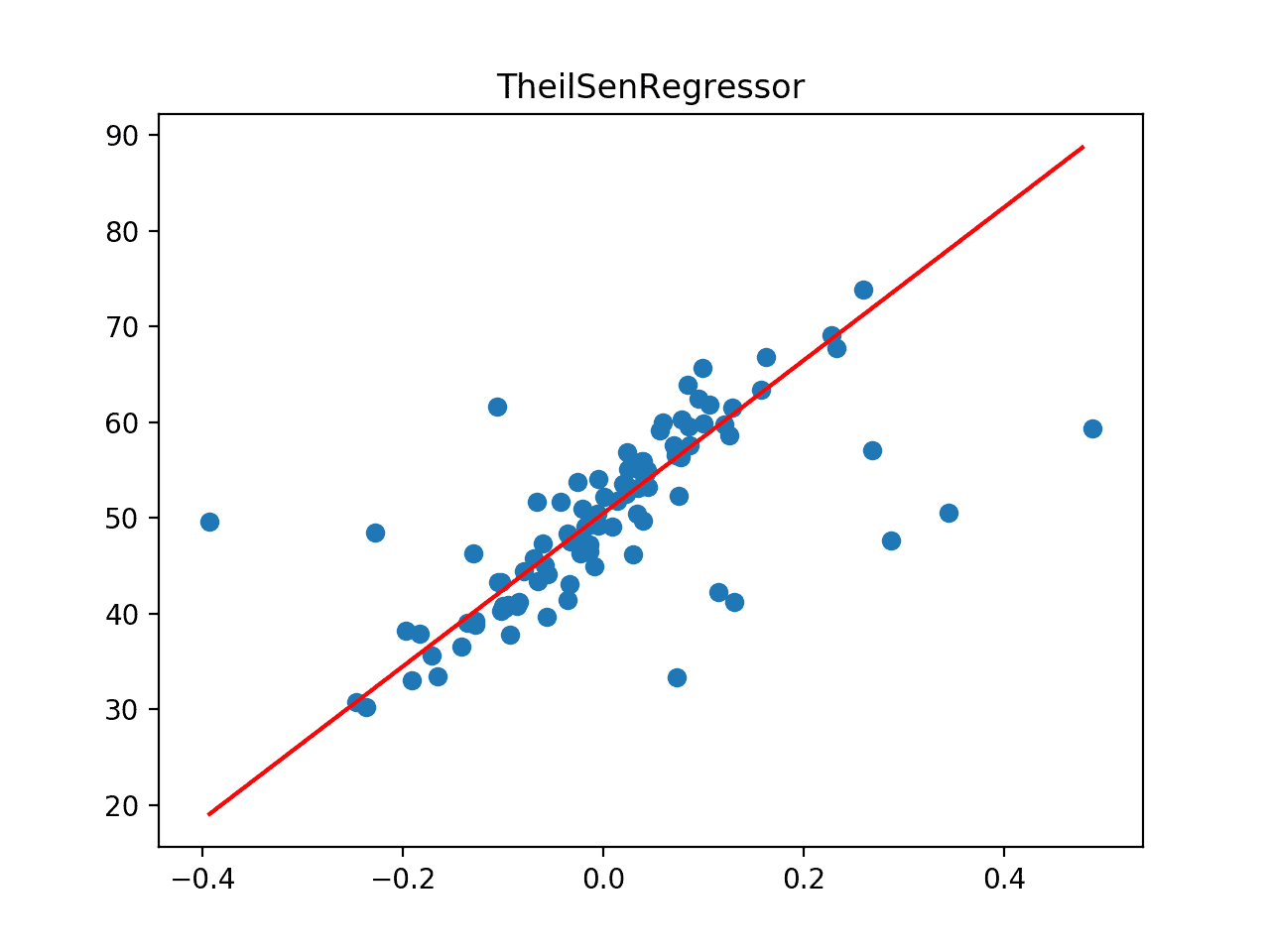
La línea de mejor ajuste para la regresión de Theil Sen en un conjunto de datos con valores atípicos
Comparar los robustos algoritmos de regresión
Ahora que estamos familiarizados con algunos robustos algoritmos de regresión populares y cómo usarlos, podemos ver cómo podríamos compararlos directamente.
Puede ser útil realizar un experimento para comparar directamente los robustos algoritmos de regresión en el mismo conjunto de datos. Podemos comparar el rendimiento medio de cada método y, más útil, utilizar herramientas como un gráfico de caja y bigote para comparar la distribución de las puntuaciones a través de los repetidos pliegues de validación cruzada.
El ejemplo completo figura a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 |
# Comparar algoritmos de regresión robustos en un conjunto de datos de regresión con valores atípicos de al azar importación al azar de al azar importación randint de al azar importación semilla de numpy importación significa de numpy importación std de numpy importación absoluto de sklearn.conjuntos de datos importación make_regression de sklearn.model_selection importación puntaje_valor_cruzado de sklearn.model_selection importación RepetidoKFold de sklearn.modelo_lineal importación LinearRegression de sklearn.modelo_lineal importación HuberRegressor de sklearn.modelo_lineal importación RANSACRegressor de sklearn.modelo_lineal importación TheilSenRegressor de matplotlib importación pyplot # Prepara el conjunto de datos def get_dataset(): X, y = make_regression(n_muestras=100, n_funciones=1, fuerza_de_cola=0.9, effective_rank=1, n_informativo=1, ruido=3, sesgo=50, estado_aleatorio=1) # Agregar algunos valores atípicos artificiales semilla(1) para i en rango(10): factor = randint(2, 4) si al azar() > 0.5: X[[i] += factor * X.std() más: X[[i] -= factor * X.std() volver X, y # Diccionario de nombres de modelos y objetos modelo def get_models(): modelos = dict() modelos[[«Lineal] = LinearRegression() modelos[[«Huber»…] = HuberRegressor() modelos[[RANSAC…] = RANSACRegressor() modelos[[TheilSen’.] = TheilSenRegressor() volver modelos # Evaluar un modelo def evalute_model(X, y, modelo, nombre): # Definir el método de evaluación del modelo cv = RepetidoKFold(n_splits=10, n_repeticiones=3, estado_aleatorio=1) # Evaluar el modelo resultados = puntaje_valor_cruzado(modelo, X, y, puntuación=‘neg_mean_absolute_error’, cv=cv, n_jobs=–1) # forzar las puntuaciones a ser positivas resultados = absoluto(resultados) volver resultados # Cargar el conjunto de datos X, y = get_dataset() # Recuperar modelos modelos = get_models() resultados = dict() para nombre, modelo en modelos.artículos(): # Evaluar el modelo resultados[[nombre] = evalute_model(X, y, modelo, nombre) # Resumir el progreso… imprimir(«>%s %.3f (%.3f) % (nombre, significa(resultados[[nombre]), std(resultados[[nombre]))) # Rendimiento del modelo de la trama para la comparación pyplot.Boxplot(resultados.valores(), etiquetas=resultados.claves(), showmeans=Verdadero) pyplot.mostrar() |
Al ejecutar el ejemplo se evalúa cada modelo a su vez, informando la media y la desviación estándar de los resultados de alcance del MAE.
Nota: sus resultados específicos diferirán dada la naturaleza estocástica de los algoritmos de aprendizaje y el procedimiento de evaluación. Intente ejecutar el ejemplo unas cuantas veces.
Podemos observar algunas diferencias menores entre estas puntuaciones y las comunicadas en la sección anterior, aunque las diferencias pueden o no ser estadísticamente significativas. El patrón general de los métodos de regresión robusta que funcionan mejor que la regresión lineal se mantiene, ya que TheilSen logra un mejor rendimiento que los otros métodos.
|
>Lineal 5.260 (1.149) >Huber 4.435 (1.868) >RANSAC 4.405 (2.206) >TheilSen 4.371 (1.961) |
Se crea un gráfico que muestra un gráfico de caja y bigote que resume la distribución de los resultados para cada algoritmo evaluado.
Podemos ver claramente las distribuciones de los robustos algoritmos de regresión sentados y extendiéndose más abajo que el algoritmo de regresión lineal.
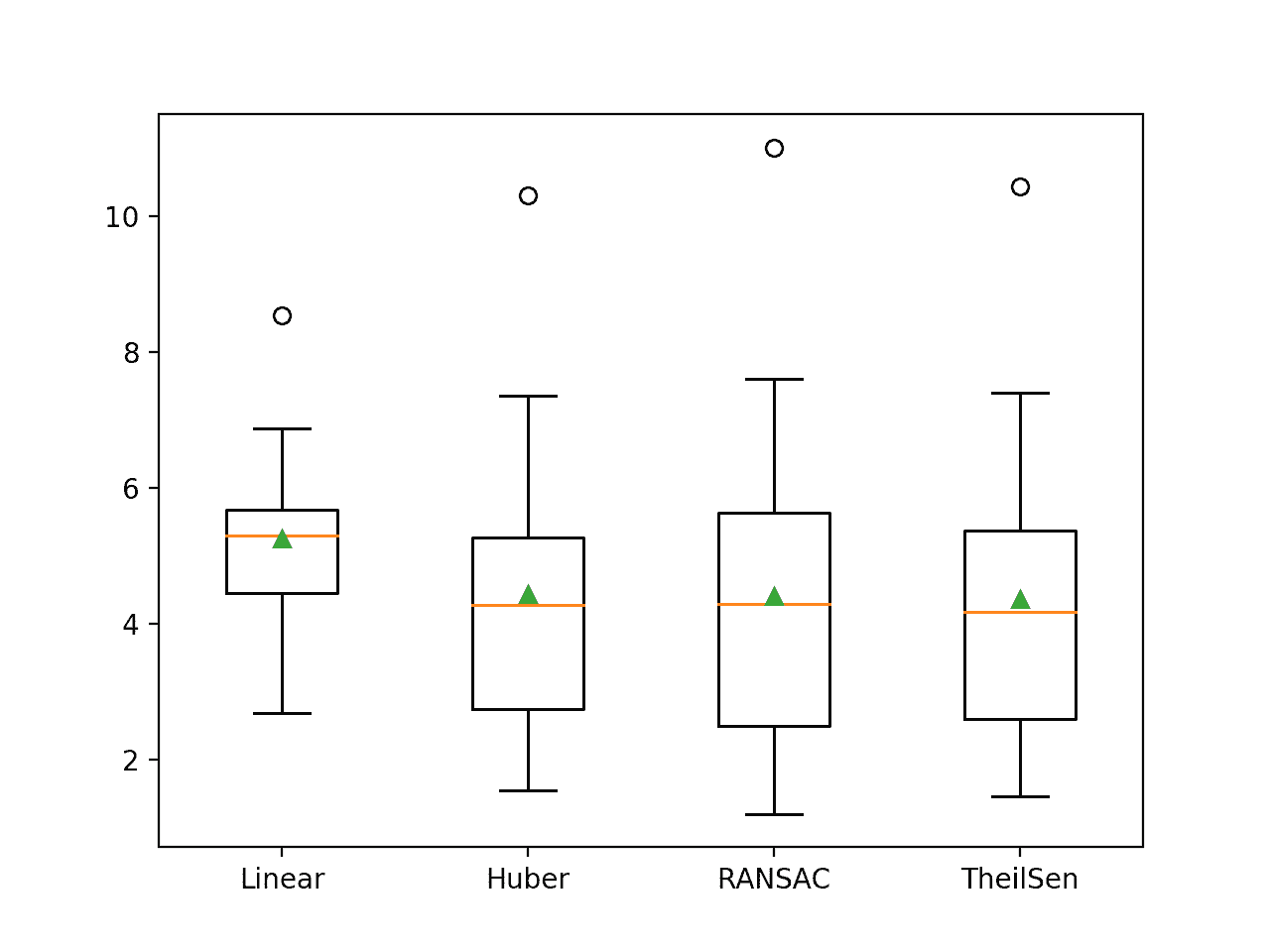
Cuadro y diagrama de bigote de las puntuaciones del MAE para los algoritmos de regresión robusta
También puede ser interesante comparar algoritmos de regresión robustos basados en una gráfica de su línea de mejor ajuste.
El ejemplo que figura a continuación se ajusta a cada algoritmo de regresión robusto y traza su línea de mejor ajuste en el mismo gráfico en el contexto de un gráfico de dispersión de todo el conjunto de datos de entrenamiento.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 |
# trazar la línea de mejor para múltiples algoritmos de regresión robusta de al azar importación al azar de al azar importación randint de al azar importación semilla de numpy importación arange de sklearn.conjuntos de datos importación make_regression de sklearn.modelo_lineal importación LinearRegression de sklearn.modelo_lineal importación HuberRegressor de sklearn.modelo_lineal importación RANSACRegressor de sklearn.modelo_lineal importación TheilSenRegressor de matplotlib importación pyplot # Prepara el conjunto de datos def get_dataset(): X, y = make_regression(n_muestras=100, n_funciones=1, fuerza_de_cola=0.9, effective_rank=1, n_informativo=1, ruido=3, sesgo=50, estado_aleatorio=1) # Agregar algunos valores atípicos artificiales semilla(1) para i en rango(10): factor = randint(2, 4) si al azar() > 0.5: X[[i] += factor * X.std() más: X[[i] -= factor * X.std() volver X, y # Diccionario de nombres de modelos y objetos modelo def get_models(): modelos = lista() modelos.anexar(LinearRegression()) modelos.anexar(HuberRegressor()) modelos.anexar(RANSACRegressor()) modelos.anexar(TheilSenRegressor()) volver modelos # Traza el conjunto de datos y la línea de mejor ajuste del modelo def plot_best_fit(X, y, xaxis, modelo): # Encajar el modelo en todos los datos modelo.encajar(X, y) # Calcular las salidas para la cuadrícula a través del dominio yaxis = modelo.predecir(xaxis.remodelar((len(xaxis), 1))) # trazar la línea de mejor ajuste pyplot.parcela(xaxis, yaxis, etiqueta=escriba(modelo).__nombre__) # Cargar el conjunto de datos X, y = get_dataset() # Definir una cuadrícula uniforme a través del dominio de entrada xaxis = arange(X.min(), X.max(), 0.01) para modelo en get_models(): # trazar la línea de mejor ajuste plot_best_fit(X, y, xaxis, modelo) # Trazar el conjunto de datos pyplot.Dispersión(X, y) # mostrar la trama pyplot.título(‘Regresión robusta’…) pyplot.leyenda() pyplot.mostrar() |
Ejecutando el ejemplo se crea un gráfico que muestra el conjunto de datos como un gráfico de dispersión y la línea de mejor ajuste para cada algoritmo.
Podemos ver claramente la línea fuera del eje para el algoritmo de regresión lineal y las líneas mucho mejores para los robustos algoritmos de regresión que siguen el cuerpo principal de los datos.
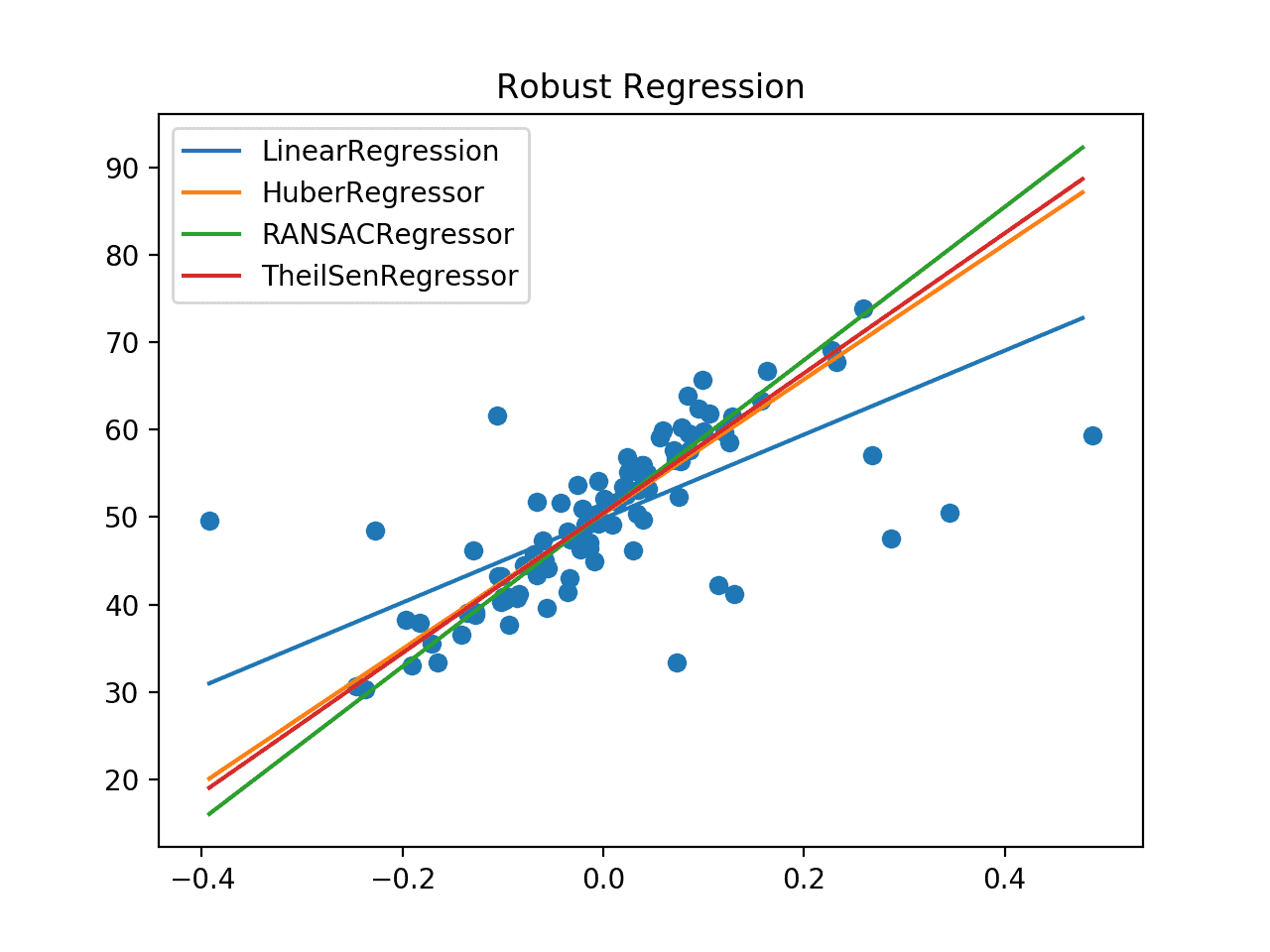
Comparación de Algoritmos de Regresión Robusta Línea de Mejor Ajuste
Más lecturas
Esta sección proporciona más recursos sobre el tema si desea profundizar en él.
APIs
Artículos
Resumen
En este tutorial, descubriste robustos algoritmos de regresión para el aprendizaje automático.
Específicamente, aprendiste:
- Se pueden utilizar robustos algoritmos de regresión para los datos con valores atípicos en los valores de entrada o de destino.
- Cómo evaluar algoritmos de regresión robustos para una tarea de modelado predictivo de regresión.
- Cómo comparar algoritmos de regresión robustos usando su línea de mejor ajuste en el conjunto de datos.
¿Tiene alguna pregunta?
Haga sus preguntas en los comentarios de abajo y haré lo posible por responder.

