El procedimiento de validación cruzada de pliegue k es un método estándar para estimar el rendimiento de un algoritmo o configuración de aprendizaje automático en un conjunto de datos.
Una sola ejecución del procedimiento de validación cruzada de pliegue k puede dar lugar a una ruidosa estimación del rendimiento del modelo. Diferentes divisiones de los datos pueden dar lugar a resultados muy diferentes.
La validación cruzada repetida de k proporciona una forma de mejorar el rendimiento estimado de un modelo de aprendizaje de máquina. Esto implica simplemente repetir el procedimiento de validación cruzada varias veces e informar el resultado medio en todos los pliegues de todas las ejecuciones. Se espera que este resultado medio sea una estimación más precisa del verdadero rendimiento medio subyacente desconocido del modelo en el conjunto de datos, calculado utilizando el error estándar.
En este tutorial, descubrirá la repetición de la validación cruzada de k-fold para la evaluación del modelo.
Después de completar este tutorial, lo sabrás:
- El promedio de rendimiento reportado de una sola corrida de validación cruzada de k puede ser ruidoso.
- La validación cruzada repetida de k proporciona una forma de reducir el error en la estimación del rendimiento medio del modelo.
- Cómo evaluar los modelos de aprendizaje de la máquina usando la validación cruzada repetida de k-fold en Python.
Empecemos.

Repetida validación cruzada de k-Fold para la evaluación del modelo en Python
Resumen del Tutorial
Este tutorial está dividido en tres partes; son:
- Validación cruzada de k-Fold
- Repetida validación cruzada del pliegue k
- Repetida validación cruzada de k-Fold en Python
Validación cruzada de k-Fold
Es común evaluar los modelos de aprendizaje de las máquinas en un conjunto de datos utilizando la validación cruzada del pliegue k.
El procedimiento de validación cruzada de pliegues k divide un conjunto limitado de datos en pliegues k no superpuestos. Cada uno de los pliegues k tiene la oportunidad de ser utilizado como un conjunto de pruebas retenidas, mientras que todos los demás pliegues colectivamente se utilizan como un conjunto de datos de entrenamiento. Un total de k modelos son ajustados y evaluados en los conjuntos de pruebas k retenidos y se informa del rendimiento medio.
Para más información sobre el procedimiento de validación cruzada de k-fold, vea el tutorial:
El procedimiento de validación cruzada de k-fold puede ser implementado fácilmente usando la biblioteca de aprendizaje de la máquina scikit-learn.
Primero, definamos un conjunto de datos de clasificación sintética que podamos usar como base de este tutorial.
La función make_classification() puede utilizarse para crear un conjunto de datos de clasificación binaria sintética. La configuraremos para generar 1.000 muestras cada una con 20 características de entrada, 15 de las cuales contribuyen a la variable objetivo.
El ejemplo que figura a continuación crea y resume el conjunto de datos.
|
# Conjunto de datos de clasificación de pruebas de sklearn.conjuntos de datos importación hacer_clasificación # Definir el conjunto de datos X, y = make_classification(n_muestras=1000, n_funciones=20, n_informativo=15, n_redundante=5, estado_aleatorio=1) # resumir el conjunto de datos imprimir(X.forma, y.forma) |
Ejecutando el ejemplo se crea el conjunto de datos y se confirma que contiene 1.000 muestras y 10 variables de entrada.
La semilla fija para el generador de números pseudoaleatorios asegura que obtengamos las mismas muestras cada vez que se genera el conjunto de datos.
A continuación, podemos evaluar un modelo en este conjunto de datos utilizando la validación cruzada del pliegue k.
Evaluaremos un modelo de LogisticRegression y usaremos la clase KFold para realizar la validación cruzada, configurada para barajar el conjunto de datos y establecer k=10, un valor predeterminado popular.
La función cross_val_score() se utilizará para realizar la evaluación, tomando la configuración del conjunto de datos y la validación cruzada y devolviendo una lista de las puntuaciones calculadas para cada pliegue.
El ejemplo completo figura a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# Evaluar un modelo de regresión logística usando validación cruzada de pliegue k de numpy importación significa de numpy importación std de sklearn.conjuntos de datos importación make_classification de sklearn.model_selection importación KFold de sklearn.model_selection importación puntaje_valor_cruzado de sklearn.modelo_lineal importación LogisticRegression # Crear un conjunto de datos X, y = make_classification(n_muestras=1000, n_funciones=20, n_informativo=15, n_redundante=5, estado_aleatorio=1) # Preparar el procedimiento de validación cruzada cv = KFold(n_splits=10, estado_aleatorio=1, shuffle=Verdadero) # Crear un modelo modelo = LogisticRegression() # Evaluar el modelo resultados = puntaje_valor_cruzado(modelo, X, y, puntuación=«exactitud, cv=cv, n_jobs=–1) # Informe de rendimiento imprimir(«Precisión: %.3f (%.3f) % (significa(resultados), std(resultados))) |
Ejecutando el ejemplo se crea el conjunto de datos, y luego se evalúa un modelo de regresión logística en él usando una validación cruzada de 10 veces. La precisión de la clasificación media en el conjunto de datos es entonces reportada.
Sus resultados específicos pueden variar dada la naturaleza estocástica del algoritmo de aprendizaje. Intente ejecutar el ejemplo unas cuantas veces.
En este caso, podemos ver que el modelo alcanzó una precisión de clasificación estimada de alrededor del 86,8 por ciento.
Ahora que estamos familiarizados con la validación cruzada del pliegue K, veamos una extensión que repite el procedimiento.
Repetida validación cruzada del pliegue k
La estimación del rendimiento del modelo a través de la validación cruzada del pliegue k puede ser ruidosa.
Esto significa que cada vez que se ejecuta el procedimiento, se puede implementar una división diferente del conjunto de datos en pliegues k, y a su vez, la distribución de las puntuaciones de rendimiento puede ser diferente, lo que da como resultado una estimación media diferente del rendimiento del modelo.
La cantidad de diferencia en el rendimiento estimado de una serie de validación cruzada de k a otra depende del modelo que se está utilizando y del propio conjunto de datos.
Una estimación ruidosa del rendimiento del modelo puede ser frustrante, ya que puede no estar claro qué resultado debe utilizarse para comparar y seleccionar un modelo final para abordar el problema.
Una solución para reducir el ruido en el rendimiento estimado del modelo es aumentar el valor k. Esto reducirá el sesgo en el rendimiento estimado del modelo, aunque aumentará la varianza: por ejemplo, vincular el resultado más al conjunto de datos específicos utilizados en la evaluación.
Un enfoque alternativo es repetir el proceso de validación cruzada del pliegue k varias veces e informar del rendimiento medio en todos los pliegues y todas las repeticiones. Este enfoque se conoce generalmente como validación cruzada repetida de pliegues K.
… la validación cruzada repetida de k-doble replica el procedimiento […] varias veces. Por ejemplo, si se repitiera cinco veces la validación cruzada 10 veces, se utilizarían 50 conjuntos diferentes de retenciones para estimar la eficacia del modelo.
– Página 70, Applied Predictive Modeling, 2013.
Es importante que cada repetición del proceso de validación cruzada del pliegue k se realice en el mismo conjunto de datos dividido en diferentes pliegues.
La validación cruzada repetida de las k-validaciones tiene el beneficio de mejorar la estimación del rendimiento medio del modelo a costa de ajustar y evaluar muchos más modelos.
Los números comunes de repeticiones incluyen 3, 5 y 10. Por ejemplo, si se utilizan 3 repeticiones de validación cruzada de 10 veces para estimar el rendimiento del modelo, esto significa que (3 * 10) o 30 modelos diferentes tendrían que ser ajustados y evaluados.
- Apropiadopara pequeños conjuntos de datos y modelos simples (por ejemplo, lineales).
Como tal, el enfoque es adecuado para conjuntos de datos y/o modelos de tamaño pequeño a modesto que no son demasiado costosos desde el punto de vista computacional para su ajuste y evaluación. Esto sugiere que el enfoque puede ser apropiado para modelos lineales y no para modelos de ajuste lento como las redes neuronales de aprendizaje profundo.
Al igual que la propia validación cruzada del pliegue k, la validación cruzada repetida del pliegue k es fácil de paralelizar, donde cada pliegue o cada proceso de validación cruzada repetida puede ejecutarse en diferentes núcleos o en diferentes máquinas.
Repetida validación cruzada de k-Fold en Python
La biblioteca de aprendizaje de la máquina Python de scikit-learn proporciona una implementación de validación cruzada de k-fold repetido a través de la clase RepeatedKFold.
Los principales parámetros son el número de pliegues (n_splits), que es el «k» en validación cruzada k, y el número de repeticiones (n_repeticiones).
Un buen valor por defecto para k es k=10.
Un buen valor por defecto para el número de repeticiones depende de cuán ruidosa sea la estimación del rendimiento del modelo en el conjunto de datos. Un valor de 3, 5 o 10 repeticiones es probablemente un buen comienzo. Es probable que no se requieran más de 10 repeticiones.
|
... # Preparar el procedimiento de validación cruzada cv = RepetidoKFold(n_splits=10, n_repeticiones=3, estado_aleatorio=1) |
El siguiente ejemplo demuestra la repetida validación cruzada de nuestro conjunto de datos de prueba.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# Evaluar un modelo de regresión logística usando una validación cruzada repetida k-pliegue de numpy importación significa de numpy importación std de sklearn.conjuntos de datos importación make_classification de sklearn.model_selection importación RepetidoKFold de sklearn.model_selection importación puntaje_valor_cruzado de sklearn.modelo_lineal importación LogisticRegression # Crear un conjunto de datos X, y = make_classification(n_muestras=1000, n_funciones=20, n_informativo=15, n_redundante=5, estado_aleatorio=1) # Preparar el procedimiento de validación cruzada cv = RepetidoKFold(n_splits=10, n_repeticiones=3, estado_aleatorio=1) # Crear un modelo modelo = LogisticRegression() # Evaluar el modelo resultados = puntaje_valor_cruzado(modelo, X, y, puntuación=«exactitud, cv=cv, n_jobs=–1) # Informe de rendimiento imprimir(«Precisión: %.3f (%.3f) % (significa(resultados), std(resultados))) |
Ejecutando el ejemplo se crea el conjunto de datos, y luego se evalúa un modelo de regresión logística en él usando una validación cruzada de 10 veces con tres repeticiones. La precisión de la clasificación media en el conjunto de datos es entonces reportada.
Sus resultados específicos pueden variar dada la naturaleza estocástica del algoritmo de aprendizaje. Intente ejecutar el ejemplo unas cuantas veces.
En este caso, podemos ver que el modelo alcanzó una precisión de clasificación estimada de alrededor del 86,7 por ciento, que es inferior al resultado de una sola corrida reportado anteriormente de 86,8 por ciento. Esto puede sugerir que el resultado de la ejecución única puede ser optimista y que el resultado de tres repeticiones podría ser una mejor estimación del verdadero rendimiento medio del modelo.
La expectativa de la validación cruzada repetida de k es que la media repetida sería una estimación más fiable del rendimiento del modelo que el resultado de un solo procedimiento de validación cruzada de k.
Esto puede significar menos ruido estadístico.
Una forma de medirlo es comparando las distribuciones de las puntuaciones medias de rendimiento bajo diferentes números de repeticiones.
Podemos imaginar que existe una verdadera media desconocida subyacente de rendimiento de un modelo en un conjunto de datos y que las repetidas ejecuciones de validación cruzada de pliegues k estiman esta media. Podemos estimar el error en el rendimiento medio a partir del verdadero rendimiento medio subyacente desconocido utilizando una herramienta estadística llamada error estándar.
El error típico puede proporcionar una indicación, para un tamaño de muestra determinado, de la cantidad de error o la propagación del error que cabe esperar de la media de la muestra a la media de la población subyacente y desconocida.
El error estándar puede calcularse de la siguiente manera:
- error_estándar = desviación_estándar_de_muestra / sqrt(número de repeticiones)
Podemos calcular el error estándar de una muestra usando la función sem() scipy.
Lo ideal sería seleccionar un número de repeticiones que muestre tanto la minimización del error estándar como la estabilización del rendimiento medio estimado en comparación con otros números de repeticiones.
El ejemplo que figura a continuación lo demuestra informando del rendimiento del modelo con una validación cruzada de 10 veces con 1 a 15 repeticiones del procedimiento.
Cabe esperar que un mayor número de repeticiones del procedimiento se traduzca en una estimación más precisa del rendimiento medio del modelo, dada la ley de los grandes números. Aunque los ensayos no son independientes, por lo que los principios estadísticos subyacentes se convierten en un reto.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
# Comparar el número de repeticiones para la validación cruzada repetida k-pliegue de scipy.estadísticas importación sem de numpy importación significa de numpy importación std de sklearn.conjuntos de datos importación make_classification de sklearn.model_selection importación RepetidoKFold de sklearn.model_selection importación puntaje_valor_cruzado de sklearn.modelo_lineal importación LogisticRegression de matplotlib importación pyplot # Evaluar un modelo con un número determinado de repeticiones def evaluate_model(X, y, repite): # Preparar el procedimiento de validación cruzada cv = RepetidoKFold(n_splits=10, n_repeticiones=repite, estado_aleatorio=1) # Crear un modelo modelo = LogisticRegression() # Evaluar el modelo resultados = puntaje_valor_cruzado(modelo, X, y, puntuación=«exactitud, cv=cv, n_jobs=–1) volver resultados # Crear un conjunto de datos X, y = make_classification(n_muestras=1000, n_funciones=20, n_informativo=15, n_redundante=5, estado_aleatorio=1) # Configuraciones a probar repite = rango(1,16) resultados = lista() para r en repite: # Evaluar usando un número dado de repeticiones resultados = evaluate_model(X, y, r) # Resumir imprimir(‘>%d media=%.4f se=%.3f’ % (r, significa(resultados), sem(resultados))) # Tienda resultados.anexar(resultados) # trazar los resultados pyplot.Boxplot(resultados, etiquetas=[[str(r) para r en repite], showmeans=Verdadero) pyplot.mostrar() |
La ejecución del ejemplo informa de la precisión de la clasificación media y estándar de los errores utilizando una validación cruzada de 10 veces con diferentes números de repeticiones.
Sus resultados específicos pueden variar dada la naturaleza estocástica del algoritmo de aprendizaje. Intente ejecutar el ejemplo unas cuantas veces.
En este caso, podemos ver que el defecto de una repetición parece optimista en comparación con los otros resultados con una precisión de alrededor del 86,80 por ciento en comparación con el 86,73 por ciento y menor con diferentes números de repeticiones.
Podemos ver que la media parece unirse alrededor de un valor de alrededor de 86,5 por ciento. Podríamos tomar esto como la estimación estable del rendimiento del modelo y, a su vez, elegir 5 o 6 repeticiones que parecen aproximarse primero a este valor.
Si observamos el error estándar, podemos ver que disminuye con el aumento del número de repeticiones y se estabiliza con un valor alrededor de 0,003 en unas 9 ó 10 repeticiones, aunque 5 repeticiones logran un error estándar de 0,005, la mitad de lo que se logra con una sola repetición.
|
>1 media=0.8680 se=0.011 >2 media=0.8675 se=0.008 >3 media=0.8673 se=0.006 >4 media=0.8670 se=0.006 >5 media=0.8658 se=0.005 >6 media=0.8655 se=0.004 >7 media=0.8651 se=0.004 >8 media=0.8651 se=0.004 >9 media=0.8656 se=0.003 >10 media=0.8658 se=0.003 >11 media=0.8655 se=0.003 >12 media=0.8654 se=0.003 >13 media=0.8652 se=0.003 >14 media=0.8651 se=0.003 >15 media=0.8653 se=0.003 |
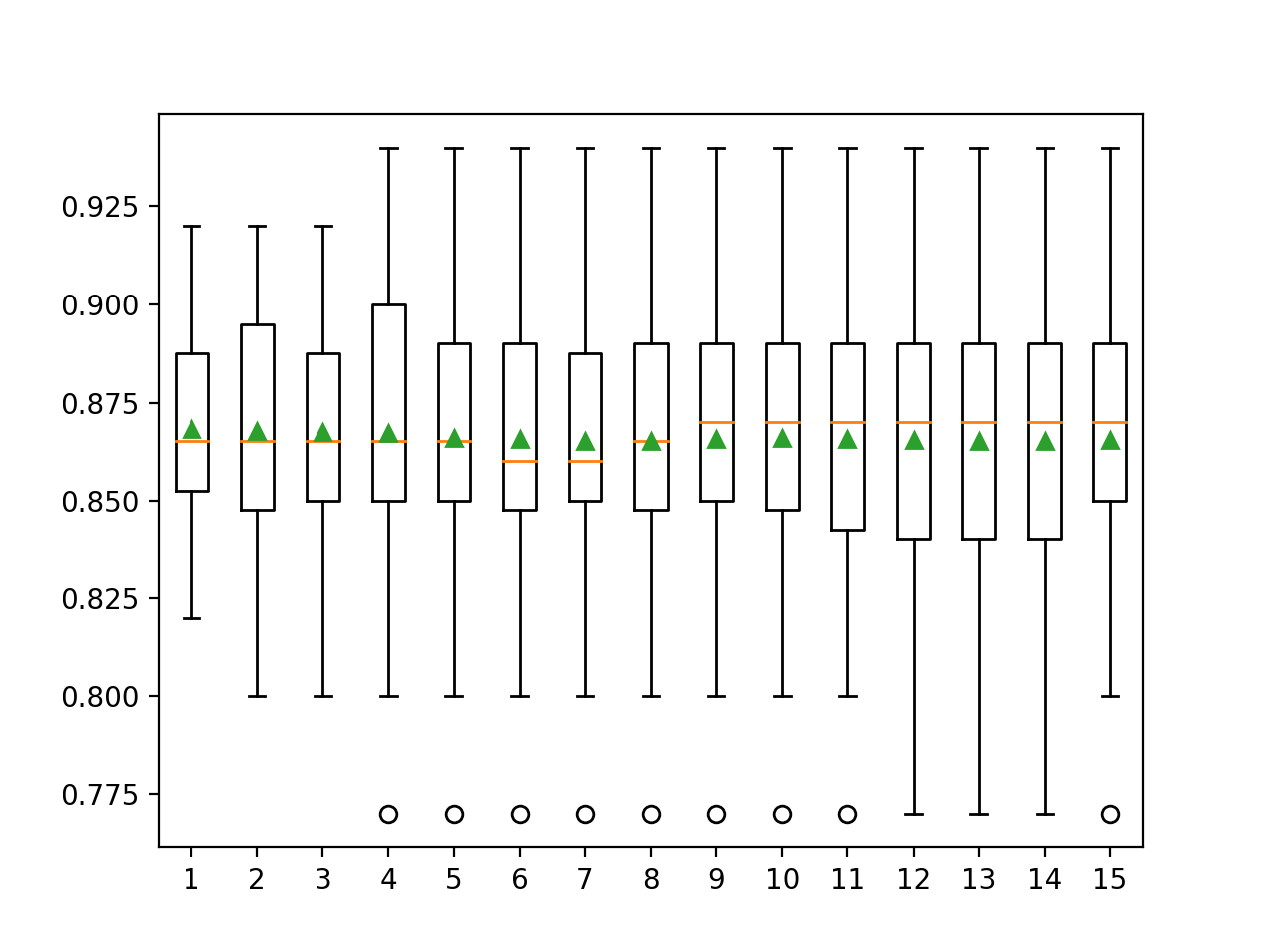
Se crea un gráfico de caja y bigote para resumir la distribución de las puntuaciones para cada número de repeticiones.
La línea naranja indica la mediana de la distribución y el triángulo verde representa la media aritmética. Si estos símbolos (valores) coinciden, sugiere una distribución simétrica razonable y que la media puede captar bien la tendencia central.
Esto podría proporcionar una heurística adicional para elegir un número apropiado de repeticiones para su arnés de prueba.
Teniendo esto en cuenta, utilizar cinco repeticiones con este arnés y algoritmo de prueba elegido parece ser una buena elección.

Cuadros y diagramas de bigote de la precisión de la clasificación frente a las repeticiones para la validación cruzada de k-Fold
