Redes Generativas Adversariales | Noviembre 2020

Las redes de adversarios generativos son una especie de algoritmo de inteligencia artificial diseñado para resolver el modelado generativo problema. El objetivo de un modelo generativo es estudiar una colección de ejemplos de capacitación y conocer la distribución de probabilidad que los generó. Las redes generativas adversas (RGA) pueden entonces generar más ejemplos a partir de la distribución de probabilidad estimada. Los modelos generativos basados en el aprendizaje profundo son comunes, pero las RGA se encuentran entre los modelos generativos más exitosos (especialmente en cuanto a su capacidad de generar imágenes realistas de alta resolución). Las GAN se han aplicado con éxito a una amplia variedad de tareas (sobre todo en entornos de investigación), pero siguen presentando desafíos y oportunidades de investigación únicos porque se basan en la teoría de los juegos, mientras que la mayoría de los demás enfoques de la modelización generativa se basan en la optimización.

Volver al principio

1. Introducción

La mayoría de los enfoques actuales para el desarrollo de la inteligencia artificial se basan principalmente en el aprendizaje de la máquina. La forma más utilizada y exitosa de aprendizaje automático hasta la fecha es el aprendizaje supervisado. Los algoritmos de aprendizaje supervisado reciben un conjunto de datos de pares de entradas y salidas de ejemplo. Aprenden a asociar cada entrada con cada salida y así aprenden un mapeo de ejemplos de entrada a salida. Los ejemplos de entrada suelen ser objetos de datos complicados como imágenes, frases en lenguaje natural o formas de onda de audio, mientras que los ejemplos de salida suelen ser relativamente sencillos. El tipo más común de aprendizaje supervisado es la clasificación, en la que la salida es sólo un código entero que identifica una categoría específica (una foto puede reconocerse como procedente de la categoría 0 que contiene gatos, o de la categoría 1 que contiene perros, etc.).

El aprendizaje supervisado suele ser capaz de lograr una precisión mayor que la humana una vez completado el proceso de capacitación, y por lo tanto se ha integrado en muchos productos y servicios. Desafortunadamente, el proceso de aprendizaje en sí mismo todavía está muy lejos de las capacidades humanas. El aprendizaje supervisado, por definición, se basa en que un supervisor humano proporcione un ejemplo de salida para cada ejemplo de entrada. Peor aún, los enfoques existentes del aprendizaje supervisado a menudo requieren millones de ejemplos de capacitación para superar el rendimiento humano, cuando un humano podría aprender a realizar la tarea aceptablemente a partir de un número muy reducido de ejemplos.

Con el fin de reducir tanto la cantidad de supervisión humana necesaria para el aprendizaje como el número de ejemplos necesarios para el aprendizaje, muchos investigadores estudian hoy en día aprendizaje no supervisadoa menudo usando… modelos generativos. En este documento de resumen, describimos un enfoque particular para el aprendizaje no supervisado a través de un modelo generativo llamado redes generativas de adversarios. Revisamos brevemente las aplicaciones de las GAN e identificamos los problemas centrales de investigación relacionados con la convergencia en los juegos necesarios para hacer de las GAN una tecnología fiable.

Volver al principio

2. 2. Modelado generativo

El objetivo del aprendizaje supervisado es relativamente sencillo de especificar, y todos los algoritmos de aprendizaje supervisado tienen esencialmente el mismo objetivo: aprender a asociar con precisión los nuevos ejemplos de entrada con las salidas correctas. Por ejemplo, un algoritmo de reconocimiento de objetos puede asociar una foto de un perro con algún tipo de DOG identificador de categoría.

El aprendizaje no supervisado es una rama menos definida del aprendizaje automático, con muchos algoritmos diferentes de aprendizaje no supervisado que persiguen muchos objetivos diferentes. En términos generales, el objetivo del aprendizaje no supervisado es aprender algo útil examinando un conjunto de datos que contenga ejemplos de entradas no etiquetadas. La agrupación y la reducción de la dimensionalidad son ejemplos comunes de aprendizaje no supervisado.

Otro enfoque para el aprendizaje no supervisado es el modelo generativo. En el modelado generativo, los ejemplos de capacitación x se extraen de una distribución desconocida p_datos(x). El objetivo de un algoritmo de modelado generativo es aprender un p_modelo(x) que se aproxima p_datos(x) lo más cerca posible.

Una forma sencilla de aprender una aproximación de p_datos es escribir explícitamente una función p_modelo(x; θ) controlado por parámetros θ y buscar el valor de los parámetros que hace que p_datos y p_modelo tan similar como sea posible. En particular, el enfoque más popular de la modelación generativa es probablemente estimación de máxima probabilidadque consiste en minimizar la divergencia Kullback-Leibler entre p_datos y p_modelo. El enfoque común de estimar el parámetro medio de una distribución gaussiana tomando la media de un conjunto de observaciones es un ejemplo de estimación de máxima probabilidad. Este enfoque basado en funciones de densidad explícitas se ilustra en la figura 1.

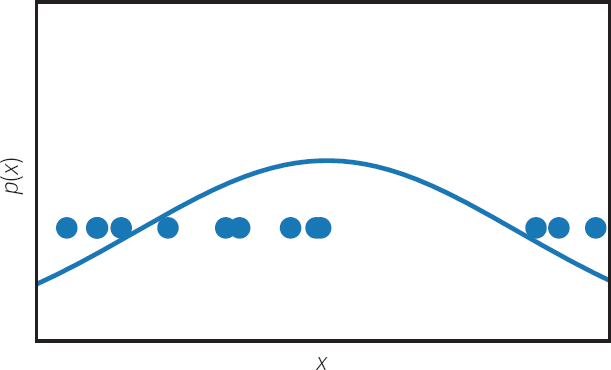
Figura 1. Muchos enfoques de la modelación generativa se basan en estimación de la densidad: observando varios ejemplos de entrenamiento de una variable aleatoria x e inferir una función de densidad p(x) que genera los datos de entrenamiento. Este enfoque se ilustra aquí, con varios puntos de datos en una línea numérica real utilizada para ajustar una función de densidad gaussiana que explica las muestras observadas. En contraste con este enfoque común, los GAN son modelos implícitos que infieren la distribución de probabilidad p(x) sin representar necesariamente la función de densidad de forma explícita.

La modelización de la densidad explícita ha funcionado bien para las estadísticas tradicionales, utilizando formas funcionales sencillas de distribuciones de probabilidad, que suelen aplicarse a un número reducido de variables. Más recientemente, con el auge del aprendizaje automático en general y del aprendizaje profundo en particular, los investigadores se han interesado por modelos de aprendizaje que utilizan formas funcionales relativamente complicadas. Cuando se utiliza una red neuronal profunda para generar datos, la función de densidad correspondiente puede ser computablemente intratable. Tradicionalmente, ha habido dos enfoques dominantes para hacer frente a este problema de intratabilidad: 1) diseñar cuidadosamente el modelo para que tenga una función de densidad manejable (por ejemplo, Frey¹¹) y (2) diseñar un algoritmo de aprendizaje basado en una aproximación computable de una función de densidad intratable (por ejemplo, Kingma y Welling¹⁵). Ambos enfoques han demostrado ser difíciles, y para muchas aplicaciones, como la generación de imágenes realistas de alta resolución, los investigadores siguen sin estar satisfechos con los resultados hasta ahora. Esto motiva a seguir investigando para mejorar estos dos caminos, pero también sugiere que un tercer camino podría ser útil.

Además de tomar un punto x como entrada y devolviendo una estimación de la probabilidad de generar ese punto, un modelo generativo puede ser útil si es capaz de generar una muestra de la distribución p_modelo. Esto se ilustra en la figura 2. Muchos modelos que representan una función de densidad también pueden generar muestras de esa función de densidad. En algunos casos, la generación de muestras es muy costosa o sólo se pueden seguir métodos aproximados de generación de muestras.

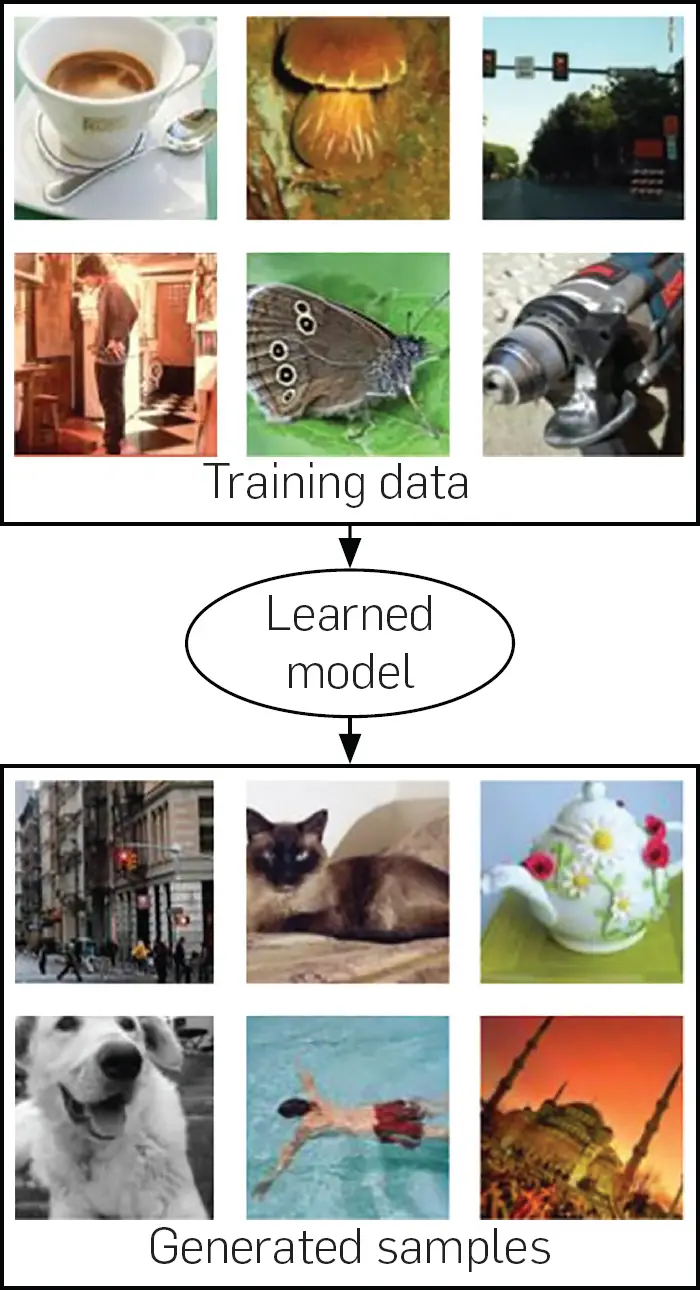
Figura 2. El objetivo de muchos modelos generativos, como se ilustra aquí, es estudiar una colección de ejemplos de capacitación, para luego aprender a generar más ejemplos que provengan de la misma distribución de probabilidad. Los GAN aprenden a hacer esto sin usar una representación explícita de la función de densidad. Una ventaja del marco de la GAN es que puede aplicarse a modelos para los cuales la función de densidad es computablemente intratable. Las muestras que se muestran aquí son todas muestras del conjunto de datos de ImageNet,⁸ incluyendo las que se llaman «muestras modelo». Utilizamos los datos reales de ImageNet para ilustrar el objetivo que alcanzaría un hipotético modelo perfecto.

Algunos modelos generativos evitan todo el problema de diseñar una función de densidad manejable y aprenden sólo un proceso de generación de muestras manejable. Estos se llaman modelos generativos implícitos. Los GAN entran en esta categoría. Antes de la introducción de las GAN, el modelo generativo implícito profundo de última generación era el red estocástica generativa⁴ que es capaz de generar aproximadamente muestras a través de un proceso incremental basado en las cadenas de Markov. Las GAN se introdujeron con el fin de crear un modelo generativo implícito profundo que fuera capaz de generar muestras verdaderas a partir de la distribución del modelo en un solo paso de generación, sin necesidad del proceso de generación incremental o de la naturaleza aproximada del muestreo de las cadenas de Markov.

Hoy en día, los enfoques más populares para el modelado generativo son probablemente los GAN, autocodificadores variacionales,¹⁵ y redes de creencias totalmente visibles (por ejemplo, Frey^{11, 26}). Ninguno de estos enfoques se basa en las cadenas de Markov, por lo que la razón del interés en las GAN hoy en día no es que hayan tenido éxito en su objetivo original de modelado generativo sin las cadenas de Markov, sino que han logrado generar imágenes de alta calidad y han demostrado ser útiles para varias tareas distintas de la generación directa, como se describe en la Sección 5.

Volver al principio

3. 3. Redes adversas generativas

Las redes de adversarios generativos se basan en un juego, en el sentido de la teoría del juego, entre dos modelos de aprendizaje por máquina, típicamente implementados utilizando redes neuronales.

Una red llamada generador define p_modelo(x) implícitamente. El generador no es necesariamente capaz de evaluar la función de densidad p_modelo. En el caso de algunas variantes de las redes de área amplia, es posible evaluar la función de densidad (cualquier modelo de densidad trazable para el que el muestreo sea trazable y diferenciable podría entrenarse como generador de redes de área amplia, como lo han hecho Danihelka et al.⁶), pero esto no es necesario. En su lugar, el generador es capaz de extraer muestras de la distribución p_modelo. El generador se define por una distribución previa p(z) sobre un vector z que sirve como entrada a la función del generador G(z; θ^(G)) donde θ^(G) es un conjunto de parámetros aprendibles que definen la estrategia del generador en el juego. El vector de entrada z puede pensarse como una fuente de aleatoriedad en un sistema por lo demás determinista, análogo a la semilla del generador de números pseudoaleatorios. La distribución anterior p(z) suele ser una distribución relativamente desestructurada, como una distribución gaussiana de alta dimensión o una distribución uniforme en un hipercubo. Muestras z de esta distribución son entonces sólo ruido. El papel principal del generador es aprender la función G(z) que transforma tal ruido desestructurado z en muestras realistas.

El otro jugador en este juego es el discriminador. El discriminador examina las muestras x y devuelve alguna estimación D(x; θ^(D)) de si x es real (extraído de la distribución de entrenamiento) o falso (extraído de p_modelo al hacer funcionar el generador). En la formulación original de los GAN, esta estimación consiste en una probabilidad de que la entrada sea real en lugar de falsa, suponiendo que la distribución real y la falsa se muestre con la misma frecuencia. Otras formulaciones (por ejemplo, Arjovsky et al.¹), pero en general, a nivel de descripciones verbales e intuitivas, el discriminador trata de predecir si la entrada fue real o falsa.

Cada jugador incurre en un costo: J^(G)(θ^(G), θ^(D)) para el generador y J^(D)(θ^(G), θ^(D)) para el discriminador. Cada jugador intenta minimizar su propio costo. A grandes rasgos, el coste del discriminador le anima a clasificar correctamente los datos como reales o falsos, mientras que el coste del generador le anima a generar muestras que el discriminador clasifica incorrectamente como reales. Son posibles muchas formulaciones específicas diferentes de estos costos y hasta ahora las formulaciones más populares parecen funcionar aproximadamente igual.¹⁸ En la versión original de las GAN, J^(D) se definió como la probabilidad negativa de registro que el discriminador asigna a las etiquetas real vs. falsa dada la entrada al discriminador. En otras palabras, el discriminador está entrenado como un clasificador binario normal. El trabajo original sobre GANs ofrecía dos versiones del coste del generador. Una versión, hoy en día llamada minimax GAN (M-GAN) definió un costo J^(G) = –J^(D)…dando un juego de minimáximo que es fácil de analizar teóricamente. M-GAN define el costo del generador cambiando el signo del costo del discriminador; otro enfoque es el GAN no saturado (NS-GAN), para lo cual el costo del generador se define volteando el discriminador etiquetas. En otras palabras, se intenta que el generador minimice la probabilidad de registro negativo que el discriminador asigna al equivocada etiquetas. Esta última ayuda a evitar la saturación del gradiente mientras se entrena al modelo.

Podemos pensar en las GAN como un poco como los falsificadores y la policía: los falsificadores hacen dinero falso mientras que la policía trata de detener a los falsificadores y sigue permitiendo el gasto de dinero legítimo. La competencia entre los falsificadores y la policía lleva a que el dinero falso sea cada vez más realista hasta que finalmente los falsificadores producen falsificaciones perfectas y la policía no puede diferenciar entre el dinero real y el falso. Una complicación de esta analogía es que el generador aprende a través del gradiente del discriminador, como si los falsificadores tuviesen un topo entre la policía informando de los métodos específicos que la policía utiliza para detectar las falsificaciones.

Este proceso se ilustra en la figura 3. La figura 4 muestra una caricatura que da una cierta intuición de cómo funciona el proceso.

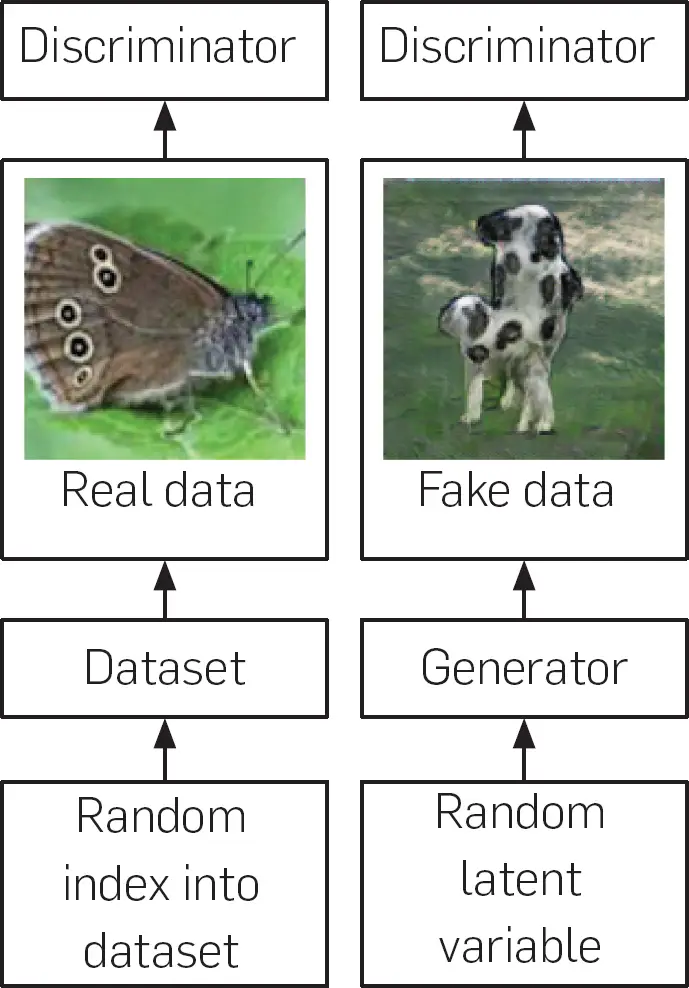
Figura 3. El entrenamiento de las GAN implica el entrenamiento de una red de generadores y una red de discriminadores. El proceso implica tanto datos reales extraídos de un conjunto de datos como datos falsos creados continuamente por el generador a lo largo del proceso de capacitación. El discriminador se entrena como cualquier otro clasificador definido por una red neural profunda. Como se muestra a la izquierda, al discriminador se le muestran los datos del conjunto de entrenamiento. En este caso, el discriminador está entrenado para asignar datos a la clase «real». Como se muestra a la derecha, el proceso de entrenamiento también incluye datos falsos. Los datos falsos se construyen mediante el primer muestreo de un vector aleatorio z a partir de una distribución previa sobre las variables latentes del modelo. El generador se utiliza entonces para producir una muestra x = G(z). La función G es simplemente una función representada por una red neuronal que transforma el azar, no estructurado z vector en datos estructurados, destinados a ser estadísticamente indistinguibles de los datos de entrenamiento. El discriminador clasifica entonces estos datos falsos. El discriminador está entrenado para asignar estos datos a la clase «falsa». El algoritmo de retropropagación permite utilizar los derivados de la salida del discriminador con respecto a la entrada del discriminador para entrenar al generador. El generador está entrenado para engañar al discriminador, en otras palabras, para hacer que el discriminador asigne su entrada a la clase «real». El proceso de formación del discriminador es, por tanto, muy similar al de cualquier otro clasificador binario, con la excepción de que los datos de la clase «falsa» proceden de una distribución que cambia constantemente a medida que el generador aprende y no de una distribución fija. El proceso de aprendizaje para el generador es algo único, porque no se le dan objetivos específicos para su salida, sino que simplemente se le da una recompensa por producir salidas que engañan a su oponente (que cambia constantemente).

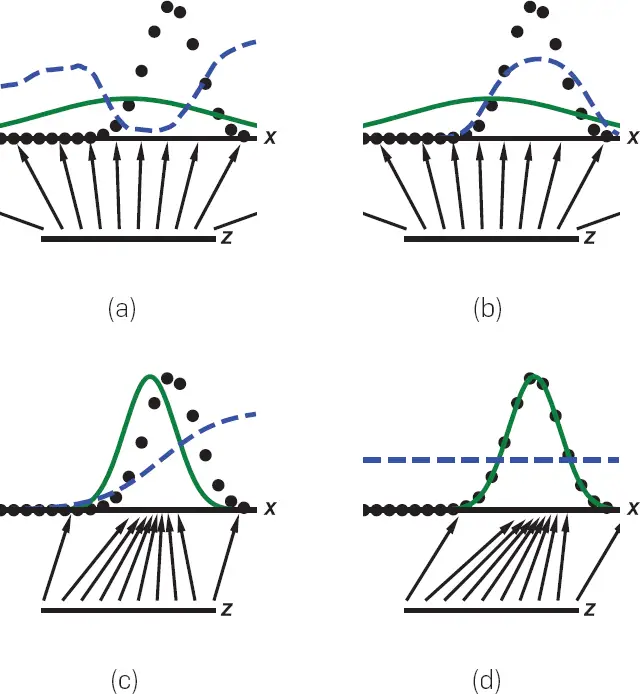
Figura 4. Una ilustración de la intuición básica del proceso de entrenamiento de GAN, ilustrada con el ajuste de una distribución Gaussiana 1-D. En este ejemplo, podemos entender el objetivo del generador como el aprendizaje de una simple escala de la función de distribución acumulativa inversa de la distribución generadora de datos. Las GAN se entrenan actualizando simultáneamente la función discriminadora (D(línea azul, línea discontinua) para que discrimine entre las muestras de la distribución generadora de datos (línea negra, línea punteada) p_x de los de la distribución generativa p_modelo (verde, línea sólida). La línea horizontal inferior es el dominio desde el cual z se muestrean, en este caso uniformemente. La línea horizontal de arriba forma parte del dominio de x. Las flechas ascendentes muestran cómo la cartografía x = G(z) impone la distribución no uniforme p_modelo en muestras transformadas. G se contrae en regiones de alta densidad y se expande en regiones de baja densidad de p_modelo. a) Considerar un par de redes de adversarios en la inicialización: p_modelo se inicializa a una unidad Gaussiana para este ejemplo mientras que D se define por una red neural profunda iniciada al azar, b) Supongamos que D fueron entrenados para la convergencia mientras G se mantuvieron fijos. En la práctica, ambos se entrenan simultáneamente, pero con el propósito de construir la intuición, vemos que si G se arreglaron, D convergerían en D* 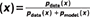. (c) Ahora supongamos que gradualmente entrenamos a ambos G y D por un tiempo. Las muestras x generada por G flujo en la dirección de aumentar D a fin de llegar a las regiones que tienen más probabilidades de ser clasificadas como datos. Mientras tanto, la estimación de D se actualiza en respuesta a esta actualización en G. d) En el equilibrio de Nash, ningún jugador puede mejorar su rendimiento porque p_modelo = p_datos. El discriminador es incapaz de diferenciar entre las dos distribuciones, es decir, D(x)=½. Esta función constante muestra que todos los puntos tienen la misma probabilidad de provenir de cualquiera de las dos distribuciones. En la práctica, G y D son típicamente optimizados con pasos de gradiente simultáneos, y no es necesario para D para ser óptimo en cada paso como se muestra en esta intuitiva caricatura. Ver Refs. Fedus et al.¹⁰ y Nagarajan y Kolter²⁴ para discusiones más realistas del proceso de equilibrio de la GAN.

La situación no es sencilla de modelar como un problema de optimización porque el costo de cada jugador es una función de los parámetros del otro jugador, pero cada jugador puede controlar sólo sus propios parámetros. Es posible reducir la situación a la optimización, donde el objetivo es minimizar

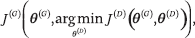
como lo demuestran Metz y otros..,²² pero la operación de argmín es difícil de trabajar de esta manera. El enfoque más popular es considerar esta situación como un juego entre dos jugadores. Gran parte de la literatura de la teoría de juegos se ocupa de juegos que tienen espacios de acción discretos y finitos, pérdidas convexas u otras propiedades que los simplifican. Las redes de área amplia requieren el uso de la teoría de juegos en entornos que aún no están bien explorados, donde los costos no son convexos y las acciones y políticas son continuas y de gran dimensión (independientemente de que consideremos que una acción es la elección de un vector de parámetro específico θ^(G) o si consideramos que la acción está generando una muestra x). El objetivo de un algoritmo de aprendizaje de máquina en este contexto es encontrar un equilibrio local de Nash²⁸un punto que es un mínimo local del costo de cada jugador con respecto a los parámetros de ese jugador. Con movimientos locales, ningún jugador puede reducir su costo aún más, asumiendo que los parámetros del otro jugador no cambien.

El algoritmo de entrenamiento más común es simplemente utilizar un optimizador basado en gradientes para tomar repetidamente pasos simultáneos en ambos jugadores, minimizando incrementalmente el costo de cada jugador con respecto a los parámetros de ese jugador.

Al final del proceso de entrenamiento, las GAN suelen ser capaces de producir muestras realistas, incluso para conjuntos de datos muy complicados que contienen imágenes de alta resolución. En la figura 5 se muestra un ejemplo.

Figura 5. Esta imagen es una muestra de una GAN progresiva¹⁴ representando a una persona que no existe pero que fue «imaginada» por una GAN después de entrenar en fotos de celebridades.

A un alto nivel, una de las razones por las que el marco de la GAN es exitoso puede ser que implica muy poca aproximación. Muchas otras aproximaciones al modelado generativo deben aproximarse a las funciones de densidad intratables. Los GAN no implican ninguna aproximación a su verdadera tarea subyacente. El único error real es el error estadístico (muestreo de una cantidad finita de datos de capacitación en lugar de medir la verdadera distribución generadora de datos subyacente) y el fracaso del algoritmo de aprendizaje para converger exactamente en los parámetros óptimos. Muchas estrategias de modelización generativa introducirían estas fuentes de error y también otras fuentes de error de aproximación, basadas en las cadenas de Markov, la optimización de los límites del costo real en lugar del costo propiamente dicho, etc.

Es difícil dar una orientación mucho más específica con respecto a los detalles de las GAN, porque las GAN son un área de investigación muy activa y la mayoría de los consejos específicos se desactualizan rápidamente. La figura 6 muestra lo rápido que han progresado las capacidades de las GAN en los años desde su introducción.

Figura 6. Una ilustración de los avances en las capacidades de las GAN en el curso de aproximadamente tres años después de la introducción de las GAN. Las GAN se han vuelto rápidamente más capaces, debido a los cambios en los algoritmos de las GAN, las mejoras en los algoritmos de aprendizaje profundo subyacentes y las mejoras en la infraestructura de software y hardware de aprendizaje profundo subyacentes. Este rápido progreso significa que es inviable que en un solo documento se resuman las capacidades más avanzadas de las GAN o cualquier conjunto específico de mejores prácticas; ambas siguen evolucionando con la suficiente rapidez como para que cualquier estudio exhaustivo quede rápidamente obsoleto. Figura reproducida con permiso de Brundage et al.⁵ Los resultados individuales son de los árbitros. Goodfellow,¹³ Karras et al.,¹⁴ Liu y Tuzel,¹⁷ y Radford y otros.²⁷ respectivamente.

Volver al principio

4. Convergencia de Gans

Los resultados teóricos centrales presentados en el documento original de la GAN¹³ eran eso:

1. en el espacio de las funciones de densidad p_modelo y funciones discriminatorias Dsólo hay un equilibrio local de Nash, donde p_modelo = p_datos.
2. si fuera posible optimizar directamente sobre tales funciones de densidad, entonces el algoritmo que consiste en optimizar D a la convergencia en el bucle interior, luego haciendo un pequeño paso de gradiente en p_modelo en el bucle exterior, converge en este equilibrio de Nash.

Sin embargo, el modelo teórico de movimientos locales directamente en el espacio de la función de densidad puede no ser muy relevante para los GAN, ya que se entrenan en la práctica: el uso de movimientos locales en parámetro espacio de la generador entre el conjunto de funciones representables por redes neuronales con un número finito de parámetros, con cada parámetro representado con un número finito de bits.

En muchos modelos teóricos diferentes, es interesante estudiar si existe un equilibrio de Nash,² si existe algún falso equilibrio de Nash,³² si el algoritmo de aprendizaje converge en un equilibrio de Nash,²⁴ y si lo hace, qué tan rápido.²¹

En muchos casos de interés práctico, estas cuestiones teóricas están abiertas, y los mejores algoritmos de aprendizaje parecen no converger empíricamente. El trabajo teórico para responder a estas preguntas está en curso, así como el trabajo para diseñar mejores costos, modelos y algoritmos de entrenamiento con mejores propiedades de convergencia.

Volver al principio

5. Otros temas de Gan

Este artículo se centra en un resumen de las principales consideraciones de diseño y propiedades algorítmicas de las GAN.

Muchos otros temas de posible interés no pueden ser considerados aquí debido a la consideración del espacio. En este artículo se discutió el uso de los GAN para aproximarse a una distribución p(x) también se han extendido al entorno condicional^23,25 donde generan muestras correspondientes a alguna entrada extrayendo muestras de la distribución condicional p(x | y). Las GAN están relacionadas con la coincidencia de momentos¹⁶ y un transporte óptimo.¹ Una peculiaridad de las GAN que se hace especialmente evidente a través de su conexión con el MMD y el transporte óptimo es que pueden ser utilizadas para entrenar modelos generativos para los cuales p_modelo tiene apoyo sólo en un colector delgado y puede realmente asignar una probabilidad cero a los datos de entrenamiento. Las GAN luchan por generar datos discretos porque el algoritmo de retropropagación necesita propagar los gradientes del discriminador a través de la salida del generador, pero este problema se está resolviendo gradualmente.⁹ Como la mayoría de los modelos generativos, los GAN pueden ser usados para llenar los huecos en los datos que faltan.³⁴ Las GAN han demostrado ser muy efectivas para aprender a clasificar datos usando muy pocos ejemplos de entrenamiento etiquetados.²⁹ La evaluación del rendimiento de los modelos generativos, incluidos los GAN, es un área de investigación difícil por sí misma.^29,31,32,33 Los GAN pueden ser vistos como una forma de que la máquina aprenda su propia función de costo, en lugar de minimizar una función de costo diseñada a mano. Las GAN pueden verse como una forma de supervisar el aprendizaje de la máquina pidiéndole que produzca cualquier salida que el propio algoritmo de aprendizaje de la máquina reconozca como aceptable, en lugar de pedirle que produzca una salida de ejemplo específica. Así pues, las GAN son excelentes para el aprendizaje en situaciones en las que hay muchas respuestas correctas posibles, como la predicción de los muchos futuros posibles que pueden ocurrir en la generación de vídeo.¹⁹ Las GAN y los modelos similares a las GAN pueden utilizarse para aprender a transformar los datos de un dominio en datos de otro dominio, incluso sin ningún par de ejemplos etiquetados de esos dominios (por ejemplo, Zhu et al.³⁵). Por ejemplo, después de estudiar una colección de fotos de cebras y una colección de fotos de caballos, los GAN pueden convertir una foto de un caballo en una foto de una cebra.³⁵ Las GAN se han utilizado en la ciencia para simular experimentos que serían costosos de ejecutar incluso en simuladores de software tradicionales.⁷ Las GAN pueden ser usadas para crear datos falsos para entrenar a otros modelos de aprendizaje de máquinas, ya sea cuando los datos reales serían difíciles de adquirir³⁰ o cuando habría problemas de privacidad asociados a los datos reales.³ Para la adaptación de los dominios se pueden utilizar modelos similares a las GAN, llamados redes de dominio-adversario.¹² Las GAN pueden ser utilizadas para una variedad de efectos de medios digitales interactivos donde el objetivo final es producir imágenes convincentes.³⁵ Los GAN pueden incluso utilizarse para resolver problemas de inferencia variacional utilizados en otros enfoques de modelación generativa.²⁰ Los GAN pueden aprender vectores de incrustación útiles y descubrir conceptos como el género de los rostros humanos sin supervisión.²⁷

Volver al principio

6. Conclusión

Los GAN son una especie de modelo generativo basado en la teoría de los juegos. Han tenido un gran éxito práctico en términos de generación de datos realistas, especialmente imágenes. Actualmente todavía es difícil entrenarlos. Para que las GANs se conviertan en una tecnología más confiable, será necesario diseñar modelos, costos o algoritmos de entrenamiento para los cuales sea posible encontrar buenos equilibrios de Nash de manera consistente y rápida.

Volver al principio

Volver al principio

Volver al principio

La Biblioteca Digital es publicada por la Asociación de Maquinaria de Computación. Derechos de autor © 2020 ACM, Inc.

No se han encontrado entradas