Los proyectos de aprendizaje de máquinas de modelado predictivo, como la clasificación y la regresión, siempre implican algún tipo de preparación de datos.
La preparación específica de los datos que se requiere para un conjunto de datos depende de las particularidades de los mismos, como los tipos de variables, así como de los algoritmos que se utilizarán para modelarlos y que pueden imponer expectativas o requisitos a los datos.
No obstante, existe una colección de algoritmos estándar de preparación de datos que pueden aplicarse a los datos estructurados (por ejemplo, los datos que forman una gran tabla como en una hoja de cálculo). Estos algoritmos de preparación de datos pueden organizarse o agruparse por tipo en un marco que puede ser útil al comparar y seleccionar técnicas para un proyecto específico.
En este tutorial, descubrirá las tareas comunes de preparación de datos realizadas en una tarea de aprendizaje de una máquina de modelado predictivo.
Después de completar este tutorial, lo sabrás:
- Técnicas como la limpieza de datos pueden identificar y corregir errores en los datos como los valores perdidos.
- Las transformaciones de datos pueden cambiar la escala, el tipo y la distribución de probabilidad de las variables del conjunto de datos.
- Técnicas como la selección de características y la reducción de la dimensionalidad pueden reducir el número de variables de entrada.
Descubre la limpieza de datos, la selección de características, la transformación de datos, la reducción de la dimensionalidad y mucho más en mi nuevo libro, con 30 tutoriales paso a paso y el código fuente completo en Python.
Empecemos.

Recorrido por las técnicas de preparación de datos para el aprendizaje automático
Foto de Nicolas Raymond, algunos derechos reservados.
Resumen del Tutorial
Este tutorial está dividido en seis partes; son:
- Tareas comunes de preparación de datos
- Limpieza de datos
- Selección de características
- Transformaciones de datos
- Ingeniería de características
- Reducción de la dimensionalidad
Tareas comunes de preparación de datos
Podemos definir la preparación de datos como la transformación de datos en bruto en una forma más adecuada para el modelado.
No obstante, hay pasos en un proyecto de modelización predictiva antes y después de la etapa de preparación de datos que son importantes e informan la preparación de datos que se va a realizar.
El proceso de aprendizaje aplicado de la máquina consiste en una secuencia de pasos.
Podemos saltar de un lado a otro entre los pasos de cualquier proyecto, pero todos los proyectos tienen los mismos pasos generales; lo son:
- Paso 1: Definir el problema.
- Paso 2: Prepare los datos.
- Paso 3: Evaluar los modelos.
- Paso 4: Finalizar el modelo.
Nos preocupa el paso de preparación de datos (paso 2), y hay tareas comunes o estándar que puede utilizar o explorar durante el paso de preparación de datos en un proyecto de aprendizaje automático.
Los tipos de preparación de datos realizados dependen de sus datos, como es de esperar.
Sin embargo, a medida que se trabaja en múltiples proyectos de modelización predictiva, se ven y requieren los mismos tipos de tareas de preparación de datos una y otra vez.
Estas tareas incluyen:
- Limpieza de datos: Identificando y corrigiendo errores o fallos en los datos.
- Selección de características: Identificar las variables de entrada más relevantes para la tarea.
- Transformaciones de datos: Cambiar la escala o distribución de las variables.
- Ingeniería de características: Derivando nuevas variables de los datos disponibles.
- Reducción de la dimensionalidad: Creando proyecciones compactas de los datos.
Esto proporciona un marco aproximado que podemos utilizar para pensar y navegar por los diferentes algoritmos de preparación de datos que podemos considerar en un proyecto determinado con datos estructurados o tabulares.
Veamos más de cerca a cada uno por separado.
Limpieza de datos
La limpieza de los datos implica arreglar problemas o errores sistemáticos en «desordenado«Datos».
La depuración de datos más útil implica un profundo conocimiento del ámbito y podría implicar la identificación y el tratamiento de observaciones específicas que pueden ser incorrectas.
Hay muchas razones por las que los datos pueden tener valores incorrectos, como estar mal escritos, corrompidos, duplicados, etc. La experiencia en el dominio puede permitir identificar observaciones obviamente erróneas ya que son diferentes de lo que se espera, como la altura de una persona de 200 pies.
Una vez que se identifican las observaciones desordenadas, ruidosas, corruptas o erróneas, pueden ser abordadas. Esto podría implicar la eliminación de una fila o una columna. Alternativamente, podría implicar el reemplazo de las observaciones con nuevos valores.
Sin embargo, hay operaciones de limpieza de datos generales que se pueden realizar, como por ejemplo:
- Utilizando estadísticas para definir los datos normales e identificar los valores atípicos.
- Identificar las columnas que tienen el mismo valor o ninguna variación y eliminarlas.
- Identificar las filas duplicadas de datos y eliminarlas.
- Marcando los valores vacíos como desaparecidos.
- Imputar los valores perdidos utilizando estadísticas o un modelo aprendido.
La limpieza de los datos es una operación que se suele realizar primero, antes de otras operaciones de preparación de datos.
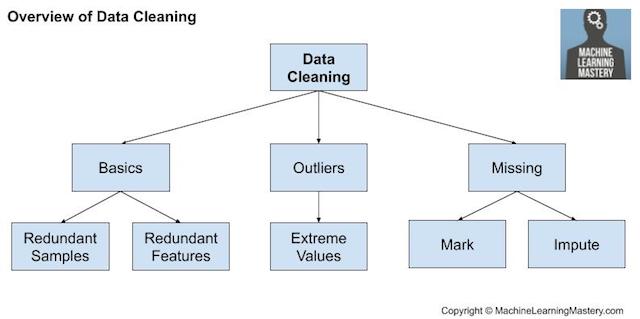
Resumen de la limpieza de datos
Para más información sobre la limpieza de datos, vea el tutorial:
Selección de características
La selección de características se refiere a las técnicas para seleccionar un subconjunto de características de entrada que son más relevantes para la variable objetivo que se está prediciendo.
Esto es importante ya que las variables de entrada irrelevantes y redundantes pueden distraer o engañar a los algoritmos de aprendizaje, lo que posiblemente resulte en un menor rendimiento de predicción. Además, es deseable desarrollar modelos sólo con los datos necesarios para hacer una predicción, por ejemplo, para favorecer el modelo más simple posible de buen rendimiento.
Las técnicas de selección de características se agrupan generalmente en aquellas que utilizan la variable objetivo (supervisado) y los que no (sin supervisión). Además, las técnicas supervisadas pueden dividirse en modelos que seleccionan automáticamente características como parte de la adaptación del modelo (intrínseco), los que explícitamente eligen características que resultan en el modelo de mejor rendimiento (envoltorio) y los que puntúan cada característica de entrada y permiten seleccionar un subconjunto (Filtro).
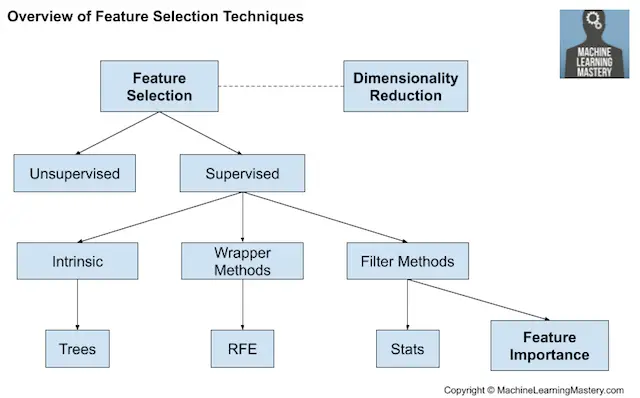
Visión general de las técnicas de selección de artículos
Los métodos estadísticos son populares para puntuar las características de entrada, como la correlación. Las características pueden ser clasificadas por sus puntuaciones y un subconjunto con las puntuaciones más grandes utilizadas como entrada de un modelo. La elección de la medida estadística depende de los tipos de datos de las variables de entrada y de un examen de las diferentes medidas estadísticas que pueden utilizarse.
Para una visión general de cómo seleccionar los métodos de selección de características estadísticas en función del tipo de datos, véase el tutorial:
Además, hay diferentes casos comunes de uso de selección de características que podemos encontrar en un proyecto de modelado predictivo, como por ejemplo:
Cuando una mezcla de datos de variables de entrada se presenta, se pueden utilizar diferentes métodos de filtrado. Alternativamente, se puede utilizar un método de envoltura como el popular método RFE que es agnóstico al tipo de variable de entrada.
El campo más amplio de la puntuación de la importancia relativa de las características de entrada se denomina importancia de las características y existen muchas técnicas basadas en modelos cuyos resultados pueden utilizarse para ayudar a interpretar el modelo, a interpretar el conjunto de datos o a seleccionar características para el modelado.
Para obtener más información sobre la importancia de las características, consulte el tutorial:
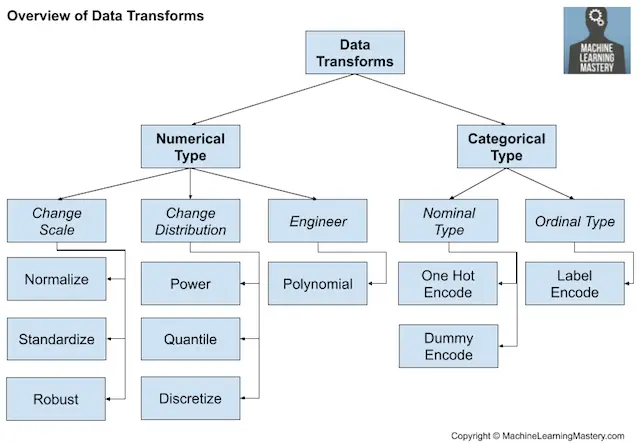
Transformaciones de datos
Las transformaciones de datos se utilizan para cambiar el tipo o la distribución de las variables de datos.
Se trata de un gran paraguas de diferentes técnicas que pueden aplicarse con la misma facilidad a las variables de entrada y salida.
Recordemos que los datos pueden ser de uno de los pocos tipos, como numérico o categóricocon subtipos para cada uno, como entero y real para numérico, y nominal, ordinal y booleano para categórico.
- Tipo de datos numéricos: Valores numéricos.
- Integro: Enteros sin parte fraccionaria.
- Real: Valores de punto flotante.
- Tipo de datos categóricos: Valores de la etiqueta.
- Ordinal: Etiquetas con un orden de rango.
- Nominal: Etiquetas sin orden de rango.
- Booleano: Valores Verdaderos y Falsos.
En la figura que figura a continuación se ofrece un panorama general de este mismo desglose de los tipos de datos de alto nivel.
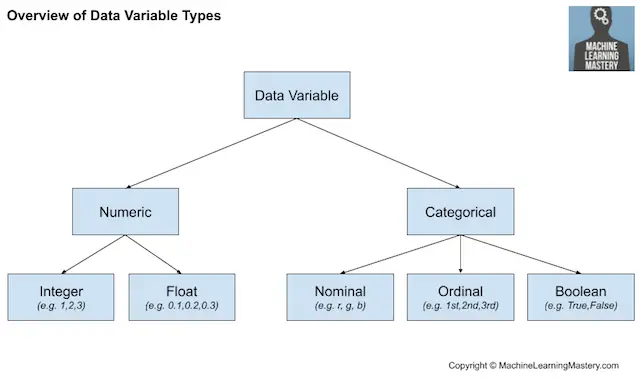
Resumen de los tipos de variables de datos
Tal vez queramos convertir una variable numérica en una variable ordinal en un proceso llamado discretización. Alternativamente, podemos codificar una variable categórica como números enteros o variables booleanas, requerido en la mayoría de las tareas de clasificación.
- Transformación de la discretización: Codificar una variable numérica como una variable ordinal.
- Transformación ordinal: Codificar una variable categórica en una variable entera.
- Transformación de una sola vez: Codificar una variable categórica en variables binarias.
En el caso de las variables numéricas de valor real, la forma en que se representan en una computadora significa que hay una resolución dramáticamente mayor en el rango 0-1 que en el rango más amplio del tipo de datos. Por ello, puede ser conveniente escalar las variables a este rango, lo que se denomina normalización. Si los datos tienen una distribución de probabilidad gaussiana, puede ser más útil desplazar los datos a un gaussiano estándar con una media de cero y una desviación estándar de uno.
- Transformación de la normalización: Escala una variable al rango 0 y 1.
- Transformación de la estandarización: Escala una variable a un Gaussiano estándar.
La distribución de probabilidad de las variables numéricas puede modificarse.
Por ejemplo, si la distribución es casi gaussiana, pero está sesgada o desplazada, puede hacerse más gaussiana utilizando una transformación de potencia. Alternativamente, las transformaciones de cuantiles pueden utilizarse para forzar una distribución de probabilidad, como la uniforme o gaussiana, en una variable con una distribución natural inusual.
- Transformación de la energía: Cambiar la distribución de una variable para que sea más gaussiana.
- Transformación de la cantidad: Imponer una distribución de probabilidad como la uniforme o la gaussiana.
Una consideración importante con las transformaciones de datos es que las operaciones se realizan generalmente por separado para cada variable. Por lo tanto, es posible que queramos realizar diferentes operaciones en diferentes tipos de variables.

Visión general de las técnicas de transformación de datos
Tal vez también queramos usar la transformación en nuevos datos en el futuro. Esto puede lograrse guardando los objetos de la transformación en un archivo junto con el modelo final entrenado en todos los datos disponibles.
Ingeniería de características
La ingeniería de características se refiere al proceso de creación de nuevas variables de entrada a partir de los datos disponibles.
La ingeniería de las nuevas características es altamente específica para sus datos y tipos de datos. Como tal, a menudo requiere la colaboración de un experto en la materia para ayudar a identificar nuevas características que podrían ser construidas a partir de los datos.
Esta especialización hace que sea un tema difícil de generalizar a los métodos generales.
Sin embargo, hay algunas técnicas que pueden ser reutilizadas, como:
- Añadiendo una variable de bandera booleana para algún estado.
- Añadiendo una estadística de grupo o resumen global, como una media.
- Añadiendo nuevas variables para cada componente de una variable compuesta, como una fecha-hora.
Un enfoque popular extraído de las estadísticas consiste en crear copias de variables de entrada numéricas que han sido modificadas con una simple operación matemática, como elevarlas a una potencia o multiplicarlas con otras variables de entrada, lo que se denomina características polinómicas.
- Transformación del polinomio: Crear copias de las variables de entrada numérica que se elevan a una potencia.
El tema de la ingeniería de las características es añadir un contexto más amplio a una observación única o descomponer una variable compleja, en ambos casos con el fin de proporcionar una perspectiva más directa de los datos de entrada.
Me gusta pensar en la ingeniería de características como un tipo de transformación de datos, aunque sería igual de razonable pensar en las transformaciones de datos como un tipo de ingeniería de características.
Reducción de la dimensionalidad
El número de características de entrada de un conjunto de datos puede considerarse la dimensionalidad de los mismos.
Por ejemplo, dos variables de entrada juntas pueden definir un área bidimensional donde cada fila de datos define un punto en ese espacio. Esta idea puede entonces escalarse a cualquier número de variables de entrada para crear grandes hipervolúmenes multidimensionales.
El problema es que, cuantas más dimensiones tenga este espacio (por ejemplo, cuantas más variables de entrada), más probable es que el conjunto de datos represente un muestreo muy escaso y probablemente no representativo de ese espacio. Esto se conoce como la maldición de la dimensionalidad.
Esto motiva la selección de características, aunque una alternativa a la selección de características es crear una proyección de los datos en un espacio de dimensiones más bajas que aún conserve las propiedades más importantes de los datos originales.
Esto se denomina generalmente reducción de la dimensionalidad y constituye una alternativa a la selección de características. A diferencia de la selección de características, las variables de los datos proyectados no están directamente relacionadas con las variables de entrada originales, lo que hace que la proyección sea difícil de interpretar.
El enfoque más común para la reducción de la dimensionalidad es utilizar una técnica de factorización de matrices:
- Análisis de Componentes Principales (PCA)
- Descomposición del Valor Singular (SVD)
El principal impacto de estas técnicas es que eliminan las dependencias lineales entre las variables de entrada, por ejemplo, las variables correlacionadas.
Existen otros enfoques que descubren una reducción de la dimensionalidad inferior. Podríamos referirnos a ellos como métodos basados en modelos como el LDA y quizás los autocodificadores.
- Análisis discriminante lineal (LDA)
A veces también se pueden utilizar múltiples algoritmos de aprendizaje, como los mapas auto-organizados de Kohonen y el t-SNE.
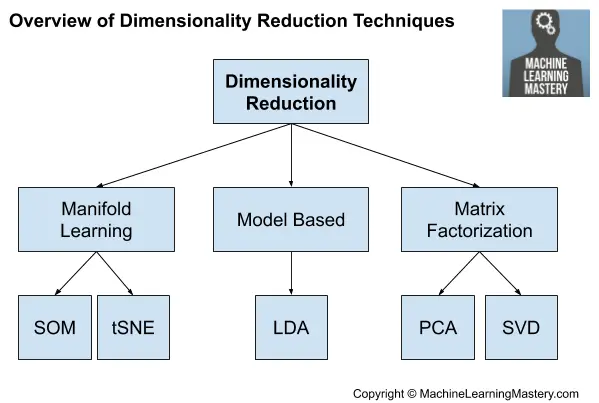
Visión general de las técnicas de reducción de la dimensionalidad
