¿Qué es un gradiente en el aprendizaje automático?

Degradado es un término de uso común en optimización y aprendizaje automático.

Por ejemplo, las redes neuronales de aprendizaje profundo se ajustan mediante el descenso de gradiente estocástico, y muchos algoritmos de optimización estándar que se utilizan para ajustar los algoritmos de aprendizaje automático utilizan información de gradiente.

Para comprender qué es un gradiente, debe comprender qué es una derivada del campo del cálculo. Esto incluye cómo calcular una derivada e interpretar el valor. La comprensión de la derivada es directamente aplicable a la comprensión de cómo calcular e interpretar gradientes como se utiliza en la optimización y el aprendizaje automático.

En este tutorial, descubrirá una suave introducción a la derivada y el gradiente en el aprendizaje automático.

Después de completar este tutorial, sabrá:

• La derivada de una función es el cambio de la función para una entrada dada.
• El gradiente es simplemente un vector derivado de una función multivariante.
• Cómo calcular e interpretar derivadas de una función simple.

Empecemos.

¿Qué es un gradiente en el aprendizaje automático?
Foto de Roanish, algunos derechos reservados.

Descripción general del tutorial

Este tutorial se divide en cinco partes; ellos son:

1. ¿Qué es una derivada?
2. ¿Qué es un degradado?
3. Ejemplo resuelto de cálculo de derivados
4. Cómo interpretar la derivada
5. Cómo calcular la derivada de una función

¿Qué es una derivada?

En cálculo, una derivada es la tasa de cambio en un punto dado en una función de valor real.

Por ejemplo, la derivada f ‘(x) de función F() para la variable x es la tasa a la que la función F() cambios en el punto X.

Podría cambiar mucho, p. Ej. ser muy curvo, o puede cambiar un poco, p. ej. curva leve, o puede que no cambie en absoluto, p. ej. plano o estacionario.

Una función es diferenciable si podemos calcular la derivada en todos los puntos de entrada para las variables de la función. No todas las funciones son diferenciables.

Una vez que calculamos la derivada, podemos usarla de varias maneras.

Por ejemplo, dado un valor de entrada X y la derivada en ese punto f ‘(x), podemos estimar el valor de la función f (x) en un punto cercano delta_x (cambiar en X) utilizando la derivada, como sigue:

• f (x + delta_x) = f (x) + f ‘(x) * delta_x

Aquí podemos ver que f ‘(x) es una línea y estamos estimando el valor de la función en un punto cercano moviéndonos a lo largo de la línea por delta_x.

Podemos usar derivadas en problemas de optimización, ya que nos dicen cómo cambiar las entradas a la función objetivo de manera que aumente o disminuya la salida de la función, para que podamos acercarnos al mínimo o al máximo de la función.

Las derivadas son útiles en la optimización porque proporcionan información sobre cómo cambiar un punto dado para mejorar la función objetivo.

– Página 32, Algoritmos de optimización, 2019.

Encontrar la línea que se puede utilizar para aproximar valores cercanos fue la razón principal para el desarrollo inicial de la diferenciación. Esta línea se conoce como la línea tangente o la pendiente de la función en un punto dado.

El problema de encontrar la recta tangente a una curva. […] implica encontrar el mismo tipo de límite […] Este tipo especial de límite se llama derivado y veremos que se puede interpretar como una tasa de cambio en cualquiera de las ciencias o ingeniería.

– Página 104, Cálculo, 8a edición, 2015.

A continuación se proporciona un ejemplo de la línea tangente de un punto para una función, tomado de la página 19 de «Algoritmos de optimización».

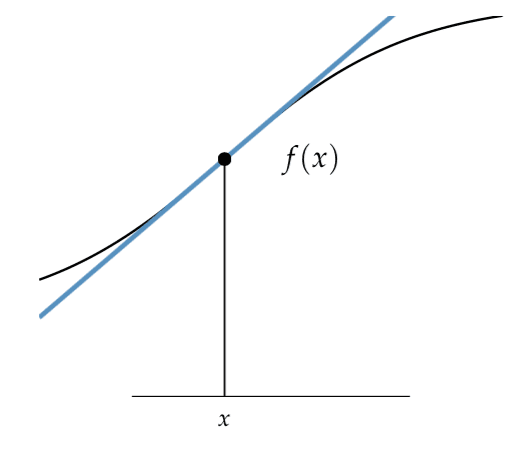
Recta tangente de una función en un punto dado
Tomado de algoritmos de optimización.

Técnicamente, la derivada descrita hasta ahora se denomina derivada de primera o derivada de primer orden.

La segunda derivada (o derivada de segundo orden) es la derivada de la función derivada. Es decir, la tasa de cambio de la tasa de cambio o cuánto cambia el cambio en la función.

• Primera derivada: Tasa de cambio de la función objetivo.
• Segunda derivada: Tasa de cambio de la función de primera derivada.

Un uso natural de la segunda derivada es aproximar la primera derivada en un punto cercano, al igual que podemos usar la primera derivada para estimar el valor de la función objetivo en un punto cercano.

Ahora que sabemos qué es una derivada, echemos un vistazo a un gradiente.

¿Qué es un degradado?

Un gradiente es una derivada de una función que tiene más de una variable de entrada.

Es un término utilizado para referirse a la derivada de una función desde la perspectiva del campo del álgebra lineal. Específicamente cuando el álgebra lineal se encuentra con el cálculo, se llama cálculo vectorial.

El gradiente es la generalización de la derivada a funciones multivariadas. Captura la pendiente local de la función, lo que nos permite predecir el efecto de dar un pequeño paso desde un punto en cualquier dirección.

– Página 21, Algoritmos de optimización, 2019.

Múltiples variables de entrada juntas definen un vector de valores, p. Ej. un punto en el espacio de entrada que se puede proporcionar a la función de destino.

De manera similar, la derivada de una función objetivo con un vector de variables de entrada es un vector. Este vector de derivadas para cada variable de entrada es el gradiente.

• Gradiente (cálculo vectorial): Un vector de derivadas para una función que toma un vector de variables de entrada.

Tal vez recuerde del álgebra de la escuela secundaria o del precálculo, el gradiente también se refiere generalmente a la pendiente de una línea en una gráfica bidimensional.

Se calcula como el aumento (cambio en el eje y) de la función dividido por la carrera (cambio en el eje x) de la función, simplificado a la regla: «levantarse sobre correr“:

• Gradiente (álgebra): Pendiente de una línea, calculada como subida sobre carrera.

Podemos ver que esta es una aproximación simple y aproximada de la derivada para una función con una variable. La función derivada del cálculo es más precisa ya que usa límites para encontrar la pendiente exacta de la función en un punto. Esta idea de gradiente del álgebra está relacionada, pero no es directamente útil, con la idea de un gradiente como se usa en optimización y aprendizaje automático.

Una función que toma múltiples variables de entrada, p. Ej. un vector de variables de entrada, puede denominarse función multivariante.

La derivada parcial de una función con respecto a una variable es la derivada asumiendo que todas las demás variables de entrada se mantienen constantes.

– Página 21, Algoritmos de optimización, 2019.

Cada componente del gradiente (vector de derivadas) se denomina derivada parcial de la función objetivo.

Una derivada parcial supone que todas las demás variables de la función se mantienen constantes.

• Derivada parcial: Derivada de una de las variables de una función multivariante.

Es útil trabajar con matrices cuadradas en álgebra lineal, y la matriz cuadrada de las derivadas de segundo orden se conoce como matriz de Hesse.

El hessiano de una función multivariante es una matriz que contiene todas las segundas derivadas con respecto a la entrada

– Página 21, Algoritmos de optimización, 2019.

Podemos usar gradiente y derivada indistintamente, aunque en los campos de optimización y aprendizaje automático, generalmente usamos «degradado”Ya que normalmente nos interesan las funciones multivariadas.

Las intuiciones para la derivada se traducen directamente al gradiente, solo que con más dimensiones.

Ahora que estamos familiarizados con la idea de derivada y gradiente, veamos un ejemplo práctico de cálculo de derivadas.

Ejemplo resuelto de cálculo de derivados

Hagamos la derivada concreta con un ejemplo trabajado.

Primero, definamos una función unidimensional simple que cuadre la entrada y defina el rango de entradas válidas de -1.0 a 1.0.

El siguiente ejemplo muestra las entradas de esta función en incrementos de 0,1, calcula el valor de la función para cada entrada y traza el resultado.

La ejecución del ejemplo crea un gráfico de líneas de las entradas de la función (eje x) y la salida calculada de la función (eje y).

Podemos ver la familiar forma de U llamada parábola.

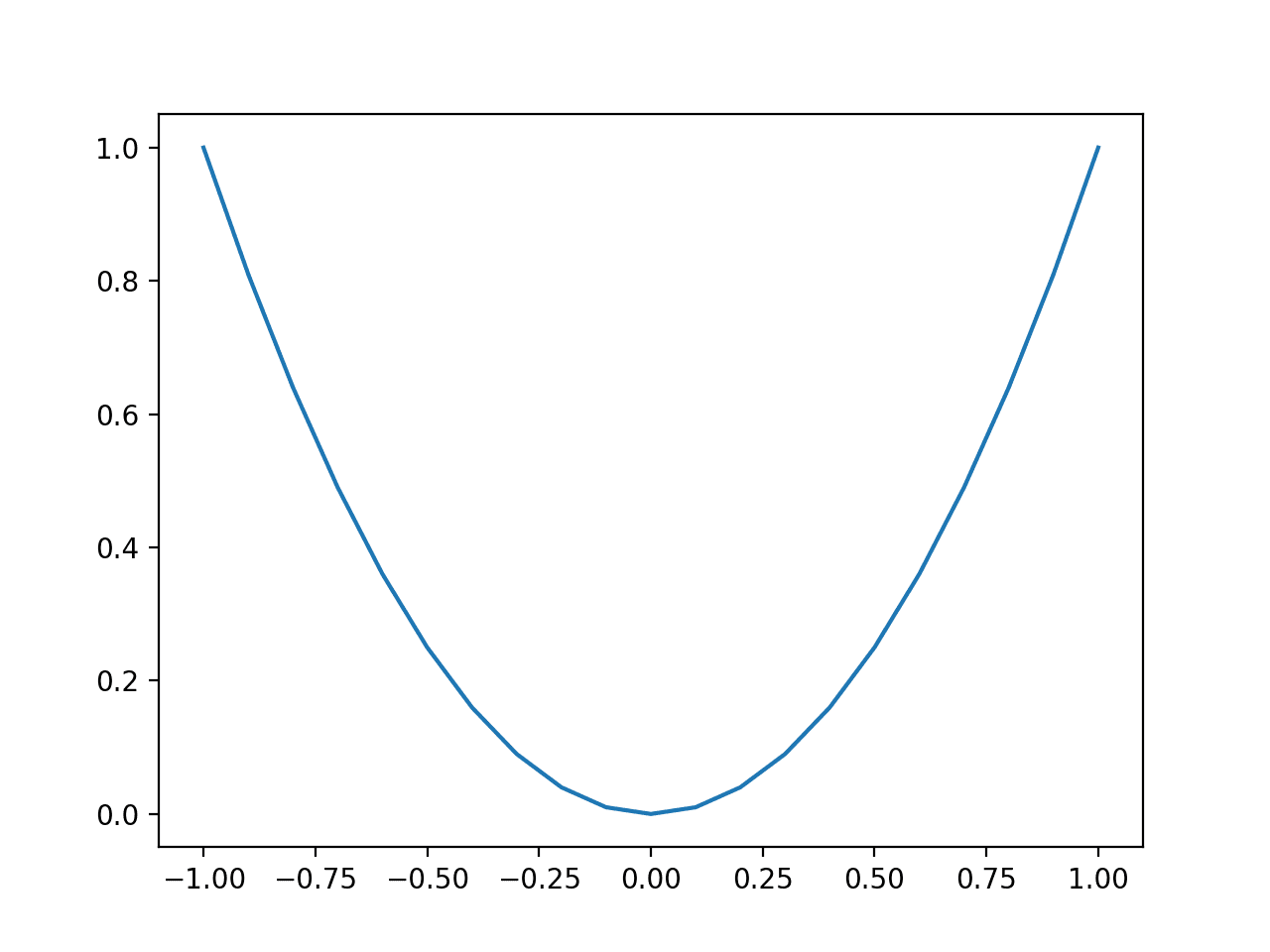
Gráfico de línea de una función unidimensional simple

Podemos ver un cambio grande o una curva pronunciada en los lados de la forma donde esperaríamos una derivada grande y un área plana en el medio de la función donde esperaríamos una derivada pequeña.

Confirmemos estas expectativas calculando la derivada en -0.5 y 0.5 (empinada) y 0.0 (plana).

La derivada de la función se calcula de la siguiente manera:

El siguiente ejemplo calcula las derivadas para los puntos de entrada específicos para nuestra función objetivo.

La ejecución del ejemplo imprime los valores derivados para valores de entrada específicos.

Podemos ver que la derivada en los puntos empinados de la función es -1 y 1 y la derivada de la parte plana de la función es 0.0.

Ahora que sabemos cómo calcular las derivadas de una función, veamos cómo podríamos interpretar los valores de las derivadas.

Cómo interpretar la derivada

El valor de la derivada se puede interpretar como la tasa de cambio (magnitud) y la dirección (signo).

• Magnitud de la derivada: Cuánto cambio.
• Signo de derivada: Dirección del cambio.

Una derivada de 0.0 indica que no hay cambios en la función objetivo, lo que se conoce como punto estacionario.

Una función puede tener uno o más puntos estacionarios y un mínimo local o global (fondo de un valle) o máximo (pico de una montaña) de la función son ejemplos de puntos estacionarios.

El gradiente apunta en la dirección del ascenso más pronunciado del hiperplano tangente …

– Página 21, Algoritmos de optimización, 2019.

El signo de la derivada le dice si la función objetivo aumenta o disminuye en ese punto.

• Derivada positiva: La función está aumentando en ese punto.
• Derivado negativo: La función está disminuyendo en ese punto

Esto puede resultar confuso porque, al observar el gráfico de la sección anterior, los valores de la función f (x) aumentan en el eje y para -0,5 y 0,5.

El truco aquí es leer siempre el gráfico de la función de izquierda a derecha, p. Ej. siga los valores en el eje y de izquierda a derecha para ingresar los valores x.

De hecho, los valores alrededor de x = -0,5 están disminuyendo si se leen de izquierda a derecha, de ahí la derivada negativa y los valores alrededor de x = 0,5 están aumentando, de ahí la derivada positiva.

Podemos imaginar que si quisiéramos encontrar los mínimos de la función en la sección anterior usando solo la información del gradiente, aumentaríamos el valor de entrada x si el gradiente fuera negativo para ir cuesta abajo, o disminuiríamos el valor de entrada x si el gradiente Fue positivo ir cuesta abajo.

Esta es la base para la clase de algoritmos de optimización de descenso de gradiente (y ascenso de gradiente) que tienen acceso a la información de gradiente de función.

Ahora que sabemos cómo interpretar los valores derivados, veamos cómo podemos encontrar la derivada de una función.

Cómo calcular la derivada de una función

Encontrar la función derivada F'() que genera la tasa de cambio de una función objetivo F() se llama diferenciación.

Hay muchos enfoques (algoritmos) para calcular la derivada de una función.

En algunos casos, podemos calcular la derivada de una función usando las herramientas de cálculo, ya sea manualmente o usando un solucionador automático.

Las clases generales de técnicas para calcular la derivada de una función incluyen:

La biblioteca SymPy Python se puede utilizar para diferenciación simbólica.

Bibliotecas computacionales como Theano y TensorFlow se puede utilizar para la diferenciación automática.

También hay servicios en línea que puede utilizar si su función es fácil de especificar en texto sin formato.

Un ejemplo es el sitio web Wolfram Alpha que calculará la derivada de la función por usted; por ejemplo:

No todas las funciones son diferenciables y algunas funciones diferenciables pueden dificultar la búsqueda de la derivada con algunos métodos.

Calcular la derivada de una función está más allá del alcance de este tutorial. Consulte un buen libro de texto de cálculo, como los de la sección de lectura adicional.

Otras lecturas

Esta sección proporciona más recursos sobre el tema si desea profundizar.

Libros

Artículos

Resumen

En este tutorial, descubrió una introducción suave a la derivada y el gradiente en el aprendizaje automático.

Específicamente, aprendiste:

• La derivada de una función es el cambio de la función para una entrada dada.
• El gradiente es simplemente un vector derivado de una función multivariante.
• Cómo calcular e interpretar derivadas de una función simple.

¿Tiene usted alguna pregunta?
Haga sus preguntas en los comentarios a continuación y haré todo lo posible para responder.