
Última actualización el 19 de junio de 2021
Cálculo es el estudio matemático del cambio.
La efectividad del cálculo para resolver un problema complicado pero continuo radica en su capacidad para dividir el problema en partes infinitamente más simples, resolverlas por separado y luego reconstruirlas en el todo original. Esta estrategia se puede aplicar para estudiar todos los elementos continuos que se pueden cortar de esta manera, ya sean las curvaturas de formas geométricas, así como la trayectoria de un objeto en vuelo, o un intervalo de tiempo.
En este tutorial, descubrirás los orígenes del cálculo y sus aplicaciones.
Después de completar este tutorial, sabrá:
- ¿Qué es el cálculo?
- ¿Cómo se puede aplicar el cálculo al mundo real?
Empecemos.

¿Qué es el cálculo?
Foto de Stephen Lammens, algunos derechos reservados.
Descripción general del tutorial
Este tutorial se divide en dos partes; ellos son:
- Cálculo
- Aplicaciones del cálculo
Cálculo
Cálculo es una palabra latina para piedra o guijarro.
El uso de esta palabra se ha filtrado en las matemáticas a partir de la antigua práctica de usar pequeñas piedras para realizar cálculos, como sumas y multiplicaciones. Si bien el uso de esta palabra ha desaparecido con el tiempo del título de muchos métodos de cálculo, una rama importante de las matemáticas la retuvo tanto que ahora nos referimos a ella como La Cálculo.
El cálculo, como otras formas de matemáticas, es mucho más que un lenguaje; también es un sistema de razonamiento increíblemente poderoso.
– Página xii, Infinite Powers, 2019.
El cálculo maduró a partir de la geometría.
En sus inicios, la geometría se preocupó por líneas rectas, planos y ángulos, reflejando sus orígenes utilitarios en la construcción de rampas y pirámides, entre otros usos. No obstante, los geómetras se encontraron sin herramientas para el estudio de círculos, esferas, cilindros y conos. Se descubrió que las áreas de superficie y los volúmenes de estas formas curvas eran mucho más difíciles de analizar que las formas rectilíneas hechas de líneas rectas y planos. A pesar de su reputación de ser complicado, el método de cálculo surgió de la búsqueda de la simplicidad, al dividir los problemas complicados en partes más simples.
Alrededor del año 250 a. C. en la antigua Grecia, era una pequeña empresa matemática dedicada al misterio de las curvas.
– Página 3, Infinite Powers, 2019.
Para ello, el cálculo giraba en torno al uso controlado del infinito como puente entre lo curvo y lo recto.
El Principio Infinito
Para arrojar luz sobre cualquier forma, objeto, movimiento, proceso o fenómeno continuo, sin importar cuán salvaje y complicado pueda parecer, vuelva a imaginarlo como una serie infinita de partes más simples, analícelas y luego sume los resultados para que tengan sentido. del todo original.
– Página xvi, Infinite Powers, 2019.
Para comprender un poco mejor este concepto, imagínese viajando en una nave espacial a la luna. Al mirar hacia afuera a la luna desde la tierra, su contorno se ve indudablemente curvo. Pero a medida que se acerca y las partes más pequeñas del contorno comienzan a llenar el puerto de visualización, la curvatura se suaviza y se vuelve menos definida. Eventualmente, la cantidad de curvatura se vuelve tan pequeña que las partes infinitesimalmente pequeñas del contorno aparecen como una línea recta. Si tuviéramos que cortar la forma circular de la luna a lo largo de estas partes infinitesimalmente pequeñas de su contorno, y luego organizar las rebanadas infinitamente pequeñas en un rectángulo, entonces podríamos calcular su área: multiplicando su ancho por su altura.
Esta es la esencia del cálculo: el avance de que si uno mira una forma curva a través de un microscopio, la parte de su curvatura sobre la que se amplía aparecerá recta y plana. Por lo tanto, analizar una forma curva es, en principio, posible al juntar sus muchas piezas rectas.
Por tanto, se puede considerar que el cálculo consta de dos fases: corte y reconstrucción.
En términos matemáticos, el proceso de corte siempre implica una resta infinitamente fina, que se utiliza para cuantificar las diferencias entre las partes. En consecuencia, esta mitad de la asignatura se denomina cálculo diferencial. El proceso de reensamblaje siempre implica una adición infinita, que integra las partes nuevamente en el todo original. Esta mitad de la asignatura se llama cálculo integral.
– Página xv, Infinite Powers, 2019.
Con esto en mente, revisemos nuestro sencillo ejemplo.
Supongamos que hemos cortado la forma circular de la luna en trozos más pequeños y que hemos reorganizado los trozos uno al lado del otro.
La forma que hemos formado es similar a un rectángulo que tiene un ancho igual a la mitad de la circunferencia del círculo, C/ 2, y una altura igual al radio del círculo, r.
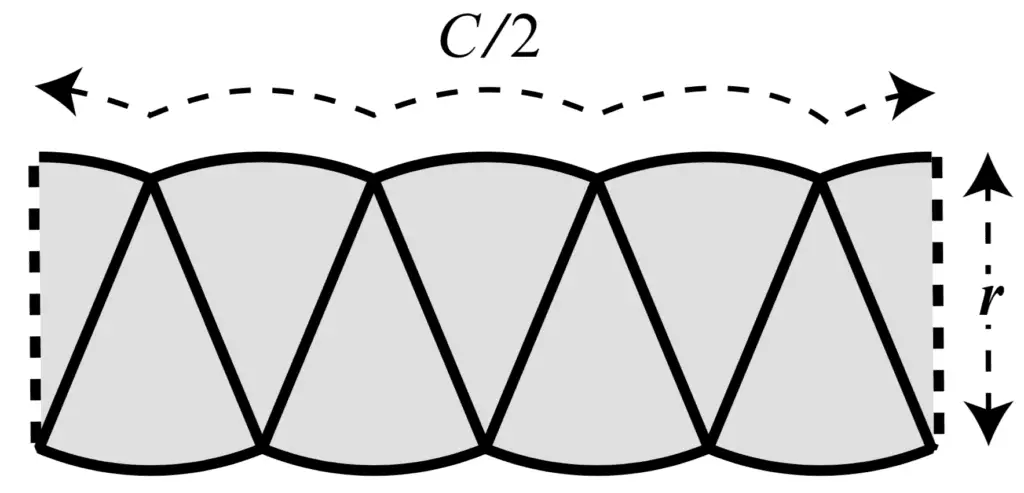
Reorganizar sectores de un círculo en un rectángulo
Tomado de Infinite Powers.
Para aplanar aún más la curvatura, podemos cortar el círculo en trozos más delgados.
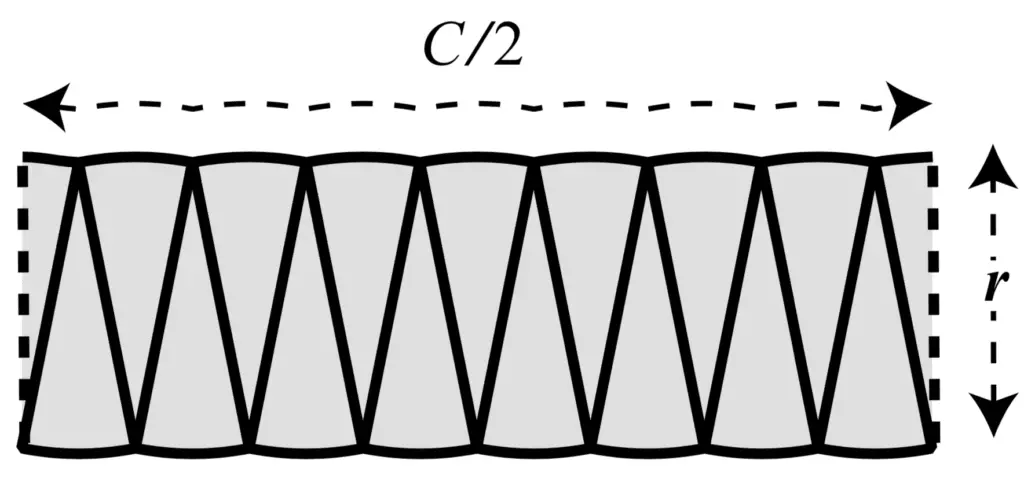
Reorganizar porciones más delgadas de un círculo en un rectángulo
Tomado de Infinite Powers.
Cuanto más finas son las rodajas, más se aplana la curvatura hasta llegar al límite de infinitamente muchas rebanadas, donde la forma ahora es perfectamente rectangular.
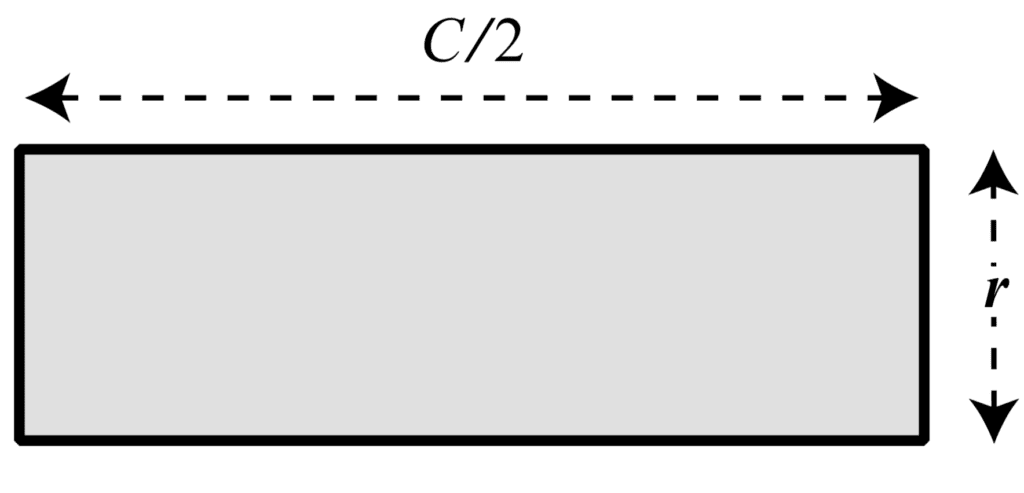
Reorganizar porciones infinitamente delgadas de un círculo en un rectángulo
Tomado de Infinite Powers.
Hemos recortado las rodajas de la forma circular y reorganizarlas en un rectángulo no cambia su área. Por lo tanto, calcular el área del círculo es equivalente a calcular el área del rectángulo resultante: A = rC/ 2.
Las curvas no solo son una característica de las formas geométricas, sino que también aparecen en la naturaleza en forma de arcos parabólicos trazados por proyectiles, o las órbitas elípticas de los planetas alrededor del sol.
Y así comenzó la segunda gran obsesión: una fascinación por los misterios del movimiento en la Tierra y en el sistema solar.
– Página xix, Infinite Powers, 2019.
Y con las curvas y el movimiento, la siguiente pregunta natural se refiere a su tasa de cambio.
Una vez resueltos los misterios de las curvas y el movimiento, el cálculo pasó a su tercera obsesión de toda la vida: el misterio del cambio.
– Página xxii, Infinite Powers, 2019.
Es a través de la aplicación del Principio de Infinito que el cálculo nos permite estudiar el movimiento y el cambio también, aproximándolos en muchos pasos infinitesimales.
Es por esta razón que el cálculo ha llegado a ser considerado el lenguaje del universo.
Aplicaciones del cálculo
El cálculo se ha aplicado en muchos dominios, desde la aplicación de Newton en la resolución de problemas de física matemática, hasta la aplicación más reciente de las ideas de Newton en el trabajo realizado en la NASA por la matemática Katherine Johnson y sus colegas.
En la década de 1860, James Clerk Maxwell usó el cálculo para reformular las leyes experimentales de la electricidad y el magnetismo, prediciendo eventualmente no solo la existencia de ondas electromagnéticas, sino también revelando la naturaleza de la luz como onda electromagnética. Sobre la base de su trabajo, Nikola Tesla creó el primer sistema de comunicación por radio, Guglielmo Marconi transmitió los primeros mensajes inalámbricos y, finalmente, surgieron muchos dispositivos modernos, como la televisión y el teléfono inteligente.
Albert Einstein, en 1917, también aplicó el cálculo a un modelo de transiciones atómicas, con el fin de predecir el efecto de la emisión estimulada. Más tarde, su trabajo condujo a los primeros láseres en funcionamiento en la década de 1960, que desde entonces se han utilizado en muchos dispositivos diferentes, como reproductores de discos compactos y lectores de códigos de barras.
Sin cálculo, no tendríamos teléfonos celulares, computadoras ni hornos microondas. No tendríamos radio. O televisión. O ultrasonido para mujeres embarazadas o GPS para viajeros perdidos. No habríamos dividido el átomo, desenmarañado el genoma humano o puesto astronautas en la luna. Puede que ni siquiera tengamos la Declaración de Independencia.
– Página vii, Infinite Powers, 2019.
Más interesante es el papel integral del cálculo en el aprendizaje automático. Es la base de algoritmos importantes, como el descenso de gradientes, que requiere el cálculo del gradiente de una función y, a menudo, es esencial para entrenar modelos de aprendizaje automático. Esto hace que el cálculo sea una de las herramientas matemáticas fundamentales en el aprendizaje automático.
Otras lecturas
Esta sección proporciona más recursos sobre el tema si desea profundizar.
Libros
Artículos
Resumen
En este tutorial, descubrió los orígenes del cálculo y sus aplicaciones.
Específicamente, aprendiste:
- Ese cálculo es el estudio matemático del cambio que se basa en una estrategia de recortar y reconstruir.
- Ese cálculo ha permitido muchos descubrimientos y la creación de muchos dispositivos modernos como los conocemos, y también es una herramienta matemática fundamental en el aprendizaje automático.
¿Tiene usted alguna pregunta?
Haga sus preguntas en los comentarios a continuación y haré todo lo posible para responder.
