En el aprendizaje por refuerzo multiagente cooperativo (MARL), debido a su en política naturaleza, se cree que los métodos de gradiente de política (PG) son menos eficientes en la muestra que los métodos de descomposición de valor (VD), que son fuera de la política. Sin embargo, algunos estudios empíricos recientes demuestran que con una representación de entrada adecuada y un ajuste de hiperparámetros, el PG multiagente puede lograr un rendimiento sorprendentemente fuerte en comparación con los métodos de VD fuera de la política.
¿Por qué los métodos de PG podrían funcionar tan bien? En esta publicación, presentaremos un análisis concreto para mostrar que en ciertos escenarios, por ejemplo, entornos con un panorama de recompensas altamente multimodal, VD puede ser problemático y conducir a resultados no deseados. Por el contrario, los métodos de PG con políticas individuales pueden converger a una política óptima en estos casos. Además, los métodos PG con políticas autorregresivas (AR) pueden aprender políticas multimodales.
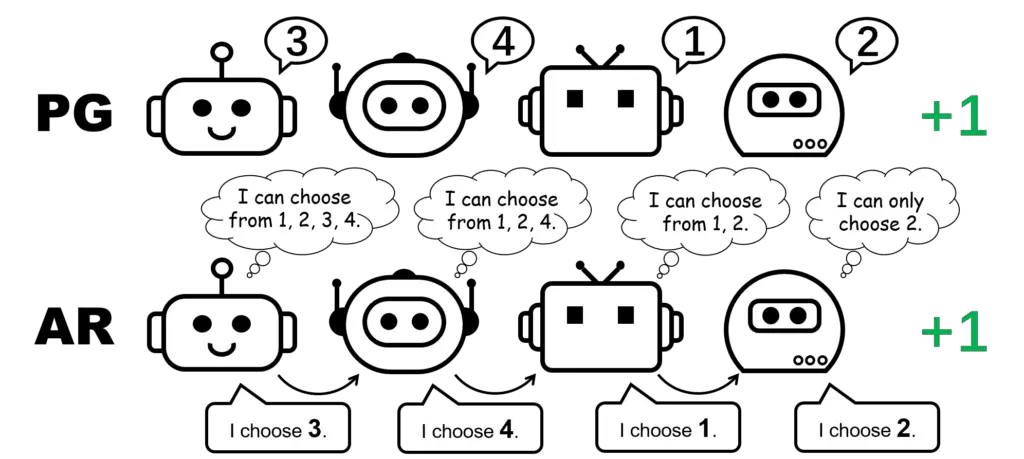
Figura 1: representación de política diferente para el juego de permutación de 4 jugadores.
CTDE en Cooperativa MARL: métodos VD y PG
La formación centralizada y la ejecución descentralizada (CTDE) es un marco popular en la cooperativa MARL. aprovecha global información para una formación más eficaz manteniendo la representación de las políticas individuales para la prueba. CTDE se puede implementar a través de descomposición de valor (VD) o gradiente de política (PG), lo que lleva a dos tipos diferentes de algoritmos.
Los métodos VD aprenden redes Q locales y una función de mezcla que mezcla las redes Q locales en una función Q global. La función de mezcla generalmente se aplica para satisfacer el principio Individual-Global-Max (IGM), que garantiza que la acción conjunta óptima se pueda calcular eligiendo con avidez la acción óptima localmente para cada agente.
Por el contrario, los métodos PG aplican directamente el gradiente de políticas para aprender una política individual y una función de valor centralizada para cada agente. La función de valor toma como entrada el estado global (p. ej., MAPPO) o la concatenación de todas las observaciones locales (p. ej., MADDPG), para una estimación precisa del valor global.
El juego de la permutación: un simple contraejemplo donde falla VD
Comenzamos nuestro análisis considerando un juego cooperativo sin estado, a saber, el juego de permutación. En un juego de permutación de $N$ jugadores, cada agente puede generar $N$ acciones ${ 1,ldots, N }$. Los agentes reciben una recompensa de $+1$ si sus acciones son mutuamente diferentes, es decir, la acción conjunta es una permutación de $1, ldots, N$; de lo contrario, reciben una recompensa de $0$. Tenga en cuenta que hay $N!$ estrategias óptimas simétricas en este juego.
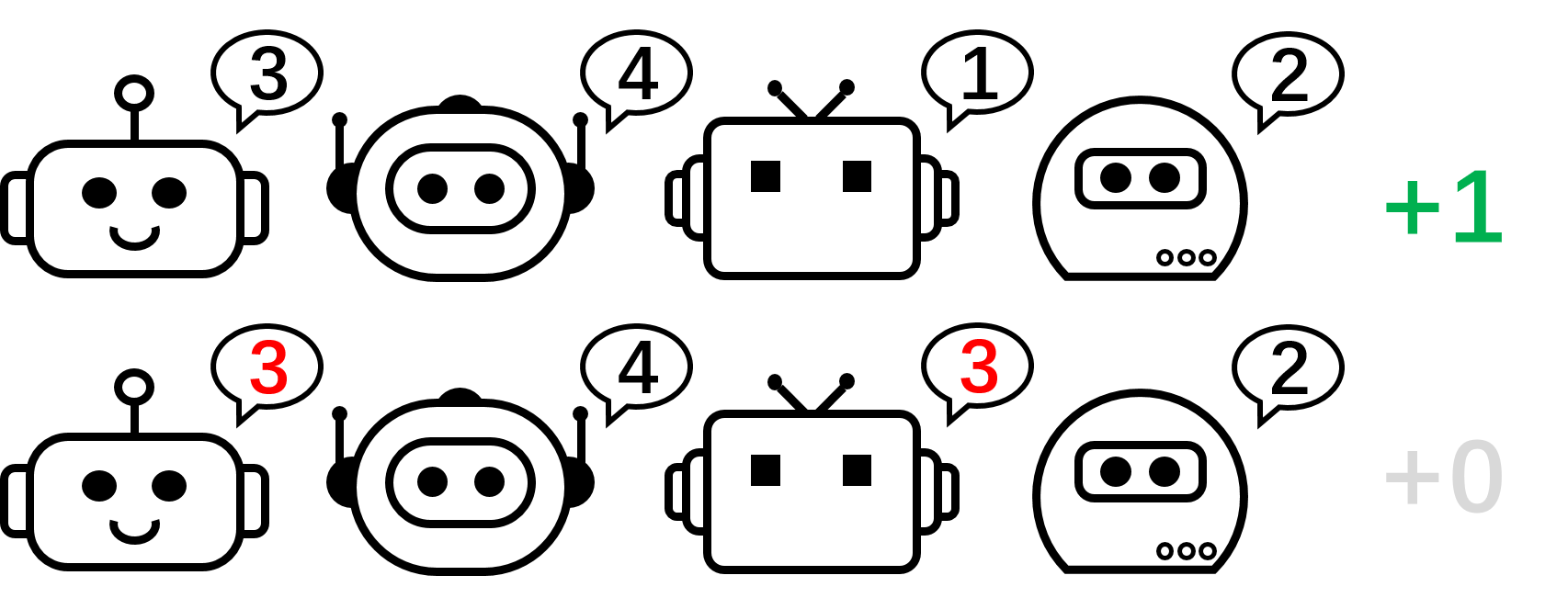
Figura 2: el juego de permutación de 4 jugadores.
Centrémonos en el juego de permutación de 2 jugadores para nuestra discusión. En esta configuración, si aplicamos VD al juego, el valor Q global se factorizará para
[Q_textrm{tot}(a^1,a^2)=f_textrm{mix}(Q_1(a^1),Q_2(a^2)),]donde $Q_1$ y $Q_2$ son funciones Q locales, $Q_textrm{tot}$ es la función Q global y $f_textrm{mix}$ es la función de mezcla que, según lo requieren los métodos VD, cumple el principio IGM.
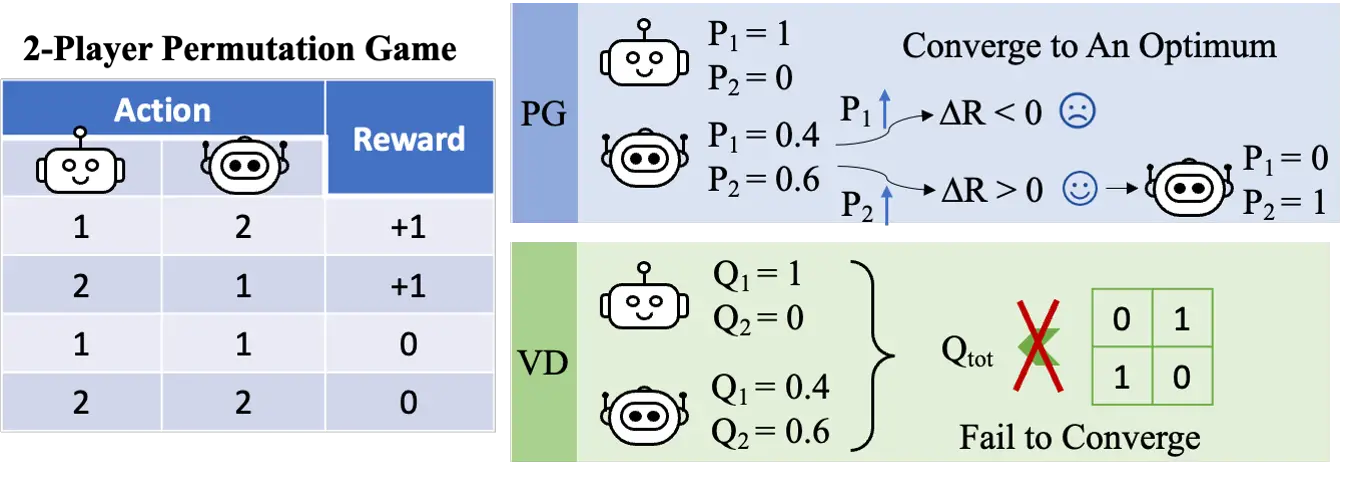
Figura 3: intuición de alto nivel sobre por qué VD falla en el juego de permutación de 2 jugadores.
Probamos formalmente que VD no puede representar el pago del juego de permutación de 2 jugadores por contradicción. Si los métodos VD pudieran representar el pago, tendríamos
[Q_textrm{tot}(1, 2)=Q_textrm{tot}(2,1)=1 qquad textrm{and} qquad Q_textrm{tot}(1, 1)=Q_textrm{tot}(2,2)=0.]Sin embargo, si cualquiera de estos dos agentes tiene valores Q locales diferentes, por ejemplo, $Q_1(1)> Q_1(2)$, entonces de acuerdo con el principio IGM, debemos tener
[1=Q_textrm{tot}(1,2)=argmax_{a^2}Q_textrm{tot}(1,a^2)>argmax_{a^2}Q_textrm{tot}(2,a^2)=Q_textrm{tot}(2,1)=1.]De lo contrario, si $Q_1(1)=Q_1(2)$ y $Q_2(1)=Q_2(2)$, entonces
[Q_textrm{tot}(1, 1)=Q_textrm{tot}(2,2)=Q_textrm{tot}(1, 2)=Q_textrm{tot}(2,1).]Como resultado, la descomposición de valores no puede representar la matriz de pagos del juego de permutación de 2 jugadores.
¿Qué pasa con los métodos PG? De hecho, las políticas individuales pueden representar una política óptima para el juego de la permutación. Además, el descenso de gradiente estocástico puede garantizar que PG converja a uno de estos óptimos bajo supuestos leves. Esto sugiere que, aunque los métodos PG son menos populares en MARL en comparación con los métodos VD, pueden ser preferibles en ciertos casos que son comunes en aplicaciones del mundo real, por ejemplo, juegos con múltiples modalidades de estrategia.
También remarcamos que en el juego de permutaciones, para representar una política conjunta óptima, cada agente debe elegir acciones distintas. En consecuencia, una implementación exitosa de PG debe garantizar que las políticas sean específicas para cada agente. Esto se puede hacer usando pólizas individuales con parámetros no compartidos (referidas como PG-Ind en nuestro documento), o una póliza condicionada por ID de agente (PG-ID).
Los PG superan a los mejores métodos de VD en los populares bancos de pruebas de MARL
Yendo más allá del simple ejemplo ilustrativo del juego de permutación, ampliamos nuestro estudio a puntos de referencia MARL populares y más realistas. Además de StarCraft Multi-Agent Challenge (SMAC), donde se verificó la efectividad de PG y la entrada de políticas condicionadas por agentes, mostramos nuevos resultados en Google Research Football (GRF) y Hanabi Challenge multijugador.
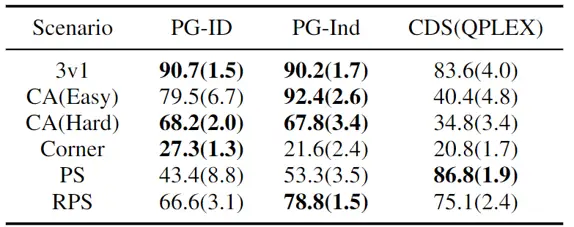
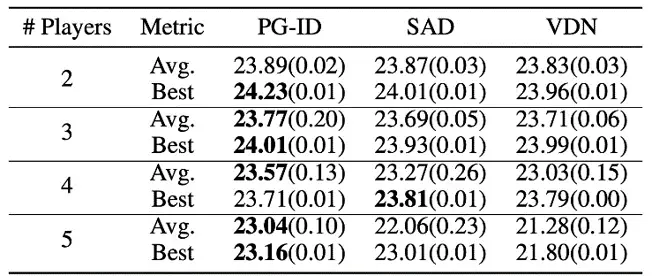
Figura 4: (izquierda) tasas de éxito de los métodos PG en GRF; (derecha) puntajes de evaluación mejores y promedio en Hanabi-Full.
En GRF, los métodos PG superan la línea de base VD (CDS) de última generación en 5 escenarios. Curiosamente, también notamos que las pólizas individuales (PG-Ind) sin compartir parámetros logran tasas de ganancia comparables, a veces incluso más altas, en comparación con las pólizas específicas de agente (PG-ID) en los 5 escenarios. Evaluamos PG-ID en el juego Hanabi a gran escala con un número variable de jugadores (2 a 5 jugadores) y los comparamos con SAD, una fuerte variante de Q-learning fuera de la política en Hanabi y Value Decomposition Networks (VDN). Como se demuestra en la tabla anterior, PG-ID puede producir resultados comparables o mejores que las recompensas mejores y promedio logradas por SAD y VDN con números variables de jugadores que usan el mismo número de pasos de entorno.
Más allá de recompensas más altas: aprendizaje de comportamiento multimodal a través de modelos de políticas autorregresivas
Además de aprender recompensas más altas, también estudiamos cómo aprender políticas multimodales en cooperativa MARL. Volvamos al juego de la permutación. Aunque hemos demostrado que PG puede aprender una política óptima de manera efectiva, el modo de estrategia que finalmente alcance puede depender en gran medida de la inicialización de la política. Así, una pregunta natural será:
¿Podemos aprender una política única que pueda cubrir todos los modos óptimos?
En la formulación del PG descentralizado, la representación factorizada de una política conjunta solo puede representar un modo particular. Por lo tanto, proponemos una forma mejorada de parametrizar las políticas para una mayor expresividad: las políticas autorregresivas (AR).

Figura 5: comparación entre políticas individuales (PG) y políticas autorregresivas (AR) en el juego de permutación de 4 jugadores.
Formalmente, factorizamos la política conjunta de $n$ agentes en la forma de
[pi(mathbf{a} mid mathbf{o}) approx prod_{i=1}^n pi_{theta^{i}} left( a^{i}mid o^{i},a^{1},ldots,a^{i-1} right),]donde la acción producida por el agente $i$ depende de su propia observación $o_i$ y de todas las acciones de los agentes anteriores $1,dots,i-1$. La factorización autorregresiva puede representar ningún política conjunta en un MDP centralizado. los solamente la modificación de la política de cada agente es la dimensión de entrada, que se amplía ligeramente al incluir acciones anteriores; y la dimensión de salida de la política de cada agente permanece sin cambios.
Con una sobrecarga de parametrización tan mínima, la política AR mejora sustancialmente el poder de representación de los métodos PG. Destacamos que PG con política AR (PG-AR) puede representar simultáneamente todos los modos de política óptimos en el juego de permutación.

Figura: los mapas de calor de acciones para políticas aprendidas por PG-Ind (izquierda) y PG-AR (centro), y el mapa de calor para recompensas (derecha); mientras que PG-Ind solo converge a un modo específico en el juego de permutación de 4 jugadores, PG-AR descubre con éxito todos los modos óptimos.
En entornos más complejos, incluidos SMAC y GRF, PG-AR puede aprender comportamientos emergentes interesantes que requieren una fuerte coordinación entre agentes que PG-Ind nunca puede aprender.

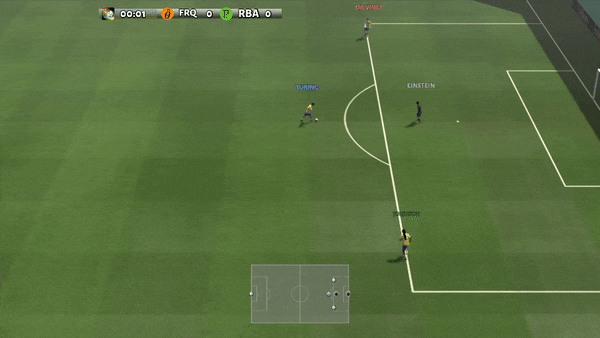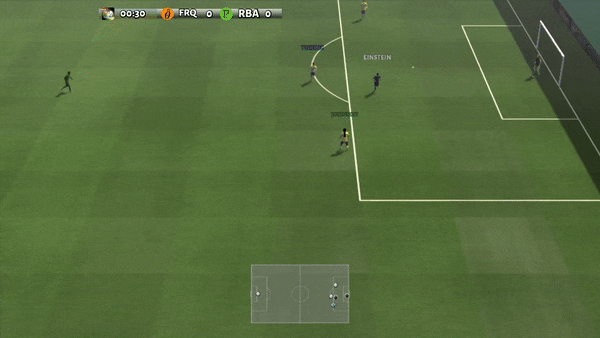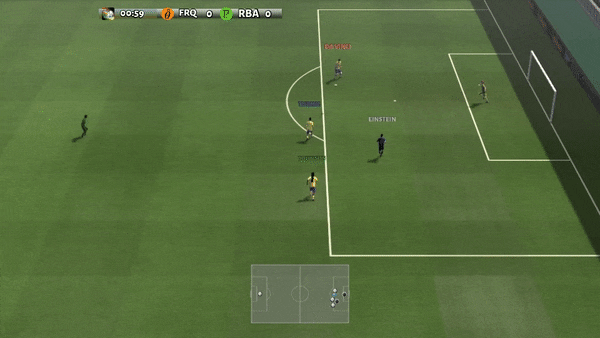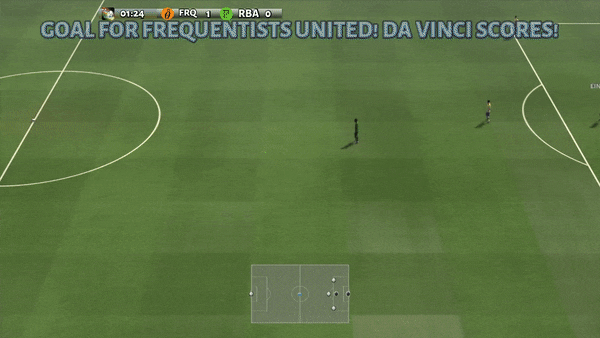
Figura 6: (izquierda) comportamiento emergente inducido por PG-AR en SMAC y GRF. En el mapa 2m_vs_1z de SMAC, los marines se mantienen de pie y atacan alternativamente mientras se aseguran de que solo haya un marine atacante en cada paso de tiempo; (derecha) en el escenario academy_3_vs_1_with_keeper de GRF, los agentes aprenden un comportamiento de estilo «Tiki-Taka»: cada jugador sigue pasando el balón a sus compañeros de equipo.
Discusiones y conclusiones
En esta publicación, proporcionamos un análisis concreto de los métodos VD y PG en cooperativa MARL. Primero, revelamos la limitación en la expresividad de los métodos VD populares, mostrando que no podrían representar políticas óptimas incluso en un juego de permutación simple. Por el contrario, mostramos que los métodos PG son probablemente más expresivos. Verificamos empíricamente la ventaja de expresividad de PG en bancos de pruebas populares de MARL, incluidos SMAC, GRF y Hanabi Challenge. Esperamos que las ideas de este trabajo puedan beneficiar a la comunidad hacia algoritmos MARL cooperativos más generales y potentes en el futuro.
Esta publicación se basa en nuestro documento en conjunto con Zelai Xu: Revisiting Some Common Practices in Cooperative Multi-Agent Reinforcement Learning (documento, sitio web).
