La regresión se refiere a problemas de modelado predictivo que implican predecir un valor numérico.
Es diferente de la clasificación que implica predecir una etiqueta de clase. A diferencia de la clasificación, no puede utilizar la precisión de la clasificación para evaluar las predicciones realizadas por un modelo de regresión.
En su lugar, debe utilizar métricas de error diseñadas específicamente para evaluar las predicciones realizadas sobre problemas de regresión.
En este tutorial, descubrirá cómo calcular métricas de error para regresión proyectos de modelado predictivo.
Después de completar este tutorial, sabrá:
- Los modelos predictivos de regresión son aquellos problemas que involucran la predicción de un valor numérico.
- Las métricas para la regresión implican calcular una puntuación de error para resumir la habilidad predictiva de un modelo.
- Cómo calcular y reportar el error cuadrático medio, el error cuadrático medio y el error absoluto medio.
Empecemos.

Métricas de regresión para el aprendizaje automático
Foto de Gael Varoquaux, algunos derechos reservados.
Descripción general del tutorial
Este tutorial se divide en tres partes; son:
- Modelado predictivo de regresión
- Evaluación de modelos de regresión
- Métricas de regresión
- Error medio cuadrado
- Error cuadrático medio
- Error absoluto medio
Modelado predictivo de regresión
El modelado predictivo es el problema de desarrollar un modelo utilizando datos históricos para hacer una predicción sobre nuevos datos donde no tenemos la respuesta.
El modelado predictivo se puede describir como el problema matemático de aproximar una función de mapeo (f) de las variables de entrada (X) a las variables de salida (y). A esto se le llama problema de aproximación de funciones.
El trabajo del algoritmo de modelado es encontrar la mejor función de mapeo que podamos teniendo en cuenta el tiempo y los recursos disponibles.
Para obtener más información sobre la aproximación de funciones en el aprendizaje automático aplicado, consulte la publicación:
El modelado predictivo de regresión es la tarea de aproximar una función de mapeo (F) de las variables de entrada (X) a una variable de salida continua (y).
La regresión es diferente de la clasificación, que implica predecir una categoría o etiqueta de clase.
Para obtener más información sobre la diferencia entre clasificación y regresión, consulte el tutorial:
Una variable de salida continua es un valor real, como un valor entero o de punto flotante. Suelen ser cantidades, como cantidades y tamaños.
Por ejemplo, se puede predecir que una casa se venderá por un valor en dólares específico, quizás en el rango de $ 100,000 a $ 200,000.
- Un problema de regresión requiere la predicción de una cantidad.
- Una regresión puede tener variables de entrada de valor real o discretas.
- Un problema con múltiples variables de entrada a menudo se denomina problema de regresión multivariante.
- Un problema de regresión en el que las variables de entrada se ordenan por tiempo se denomina problema de pronóstico de series de tiempo.
Ahora que estamos familiarizados con el modelo predictivo de regresión, veamos cómo podemos evaluar un modelo de regresión.
Evaluación de modelos de regresión
Una pregunta común de los principiantes en los proyectos de modelado predictivo de regresión es:
¿Cómo calculo la precisión de mi modelo de regresión?
La precisión (por ejemplo, la precisión de la clasificación) es una medida de clasificación, no de regresión.
Nosotros no puedo calcular la precisión para un modelo de regresión.
La habilidad o el desempeño de un modelo de regresión se debe informar como un error en esas predicciones.
Esto tiene sentido si lo piensas bien. Si está prediciendo un valor numérico como una altura o una cantidad en dólares, no querrá saber si el modelo predijo el valor exactamente (esto puede ser increíblemente difícil en la práctica); en cambio, queremos saber qué tan cerca estaban las predicciones de los valores esperados.
Error aborda exactamente esto y resume en promedio qué tan cerca estaban las predicciones de sus valores esperados.
Hay tres métricas de error que se usan comúnmente para evaluar y reportar el desempeño de un modelo de regresión; son:
- Error cuadrático medio (MSE).
- Error cuadrático medio (RMSE).
- Error absoluto medio (MAE)
Hay muchas otras métricas de regresión, aunque estas son las más utilizadas. Puede ver la lista completa de métricas de regresión compatibles con la biblioteca de aprendizaje automático de Python de scikit-learn aquí:
En la siguiente sección, echemos un vistazo más de cerca a cada uno de ellos.
Métricas de regresión
En esta sección, analizaremos más de cerca las métricas populares para los modelos de regresión y cómo calcularlas para su proyecto de modelado predictivo.
Error medio cuadrado
Mean Squared Error, o MSE para abreviar, es una métrica de error popular para problemas de regresión.
También es una función de pérdida importante para los algoritmos ajustados u optimizados utilizando el marco de mínimos cuadrados de un problema de regresión. Aquí «mínimos cuadrados”Se refiere a minimizar el error cuadrático medio entre las predicciones y los valores esperados.
El MSE se calcula como la media o el promedio de las diferencias al cuadrado entre los valores objetivo predichos y esperados en un conjunto de datos.
- MSE = 1 / N * suma de i a N (y_i – yhat_i) ^ 2
Dónde y_i es el i-ésimo valor esperado en el conjunto de datos y yhat_i es el iésimo valor predicho. La diferencia entre estos dos valores se eleva al cuadrado, lo que tiene el efecto de eliminar el signo, lo que da como resultado un valor de error positivo.
La cuadratura también tiene el efecto de inflar o magnificar errores grandes. Es decir, cuanto mayor sea la diferencia entre los valores predichos y esperados, mayor será el error cuadrado positivo resultante. Esto tiene el efecto de «agotador”Modela más para errores mayores cuando MSE se usa como función de pérdida. También tiene el efecto de «agotador”Inflando la puntuación de error promedio cuando se usa como métrica.
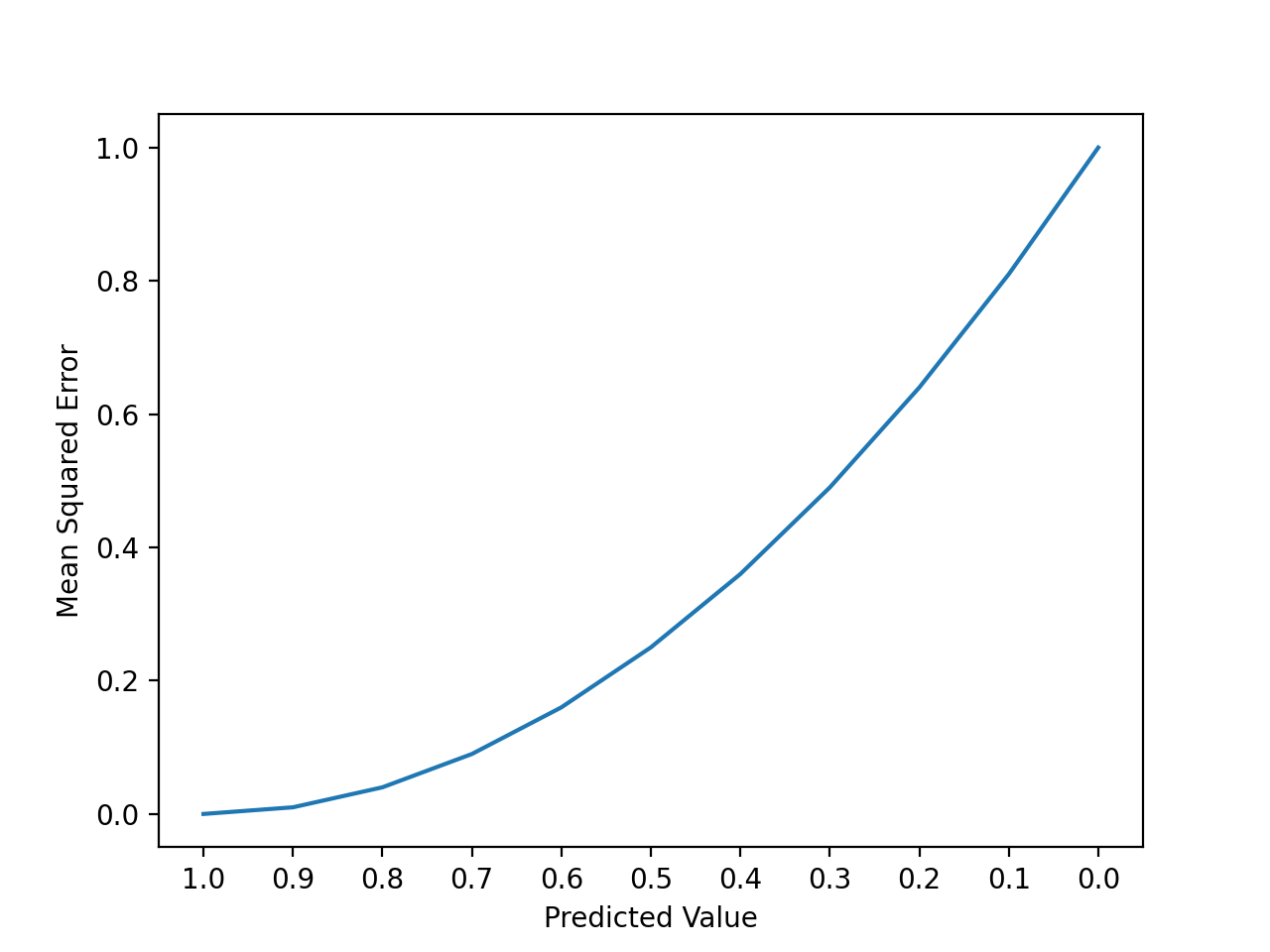
Podemos crear una gráfica para tener una idea de cómo el cambio en el error de predicción impacta el error al cuadrado.
El siguiente ejemplo proporciona un pequeño conjunto de datos artificial de todos los valores 1.0 y predicciones que van desde perfecto (1.0) a incorrecto (0.0) en incrementos de 0.1. El error al cuadrado entre cada predicción y el valor esperado se calcula y se traza para mostrar el aumento cuadrático del error al cuadrado.
|
... # calcular error errar = (esperado[[yo] – predicho[[yo])**2 |
El ejemplo completo se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 |
# ejemplo de aumento del error cuadrático medio desde matplotlib importar pyplot desde sklearn.métrica importar mean_squared_error # valor real esperado = [[1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0] # valor predicho predicho = [[1.0, 0,9, 0.8, 0,7, 0,6, 0,5, 0.4, 0,3, 0,2, 0,1, 0.0] # calcular errores errores = lista() para yo en rango(len(esperado)): # calcular error errar = (esperado[[yo] – predicho[[yo])**2 # error de tienda errores.adjuntar(errar) # informe de error impresión(‘>%. 1f,% .1f =% .3f’ % (esperado[[yo], predicho[[yo], errar)) # errores de trazado pyplot.trama(errores) pyplot.xticks(garrapatas=[[yo para yo en rango(len(errores))], etiquetas=predicho) pyplot.xlabel(‘Valor previsto’) pyplot.etiquetarse(‘Error medio cuadrado’) pyplot.show() |
Ejecutar el ejemplo primero informa el valor esperado, el valor predicho y el error al cuadrado para cada caso.
Podemos ver que el error aumenta rápidamente, más rápido que lineal (una línea recta).
|
> 1.0, 1.0 = 0.000 > 1.0, 0.9 = 0.010 > 1.0, 0.8 = 0.040 > 1.0, 0.7 = 0.090 > 1.0, 0.6 = 0.160 > 1.0, 0.5 = 0.250 > 1.0, 0.4 = 0.360 > 1.0, 0.3 = 0.490 > 1.0, 0.2 = 0.640 > 1.0, 0.1 = 0.810 > 1.0, 0.0 = 1.000 |
Se crea un gráfico de líneas que muestra el aumento curvo o superlineal del valor del error al cuadrado a medida que aumenta la diferencia entre el valor esperado y el predicho.
La curva no es una línea recta como podríamos asumir ingenuamente para una métrica de error.

Gráfica lineal del error cuadrático creciente con predicciones
Los términos de error individuales se promedian para que podamos informar el rendimiento de un modelo con respecto a cuánto error comete el modelo en general al hacer predicciones, en lugar de específicamente para un ejemplo dado.
Las unidades del MSE son unidades cuadradas.
Por ejemplo, si su valor objetivo representa «dolares, «Entonces el MSE será»dólares al cuadrado. » Esto puede resultar confuso para las partes interesadas; por lo tanto, al informar los resultados, a menudo se usa en su lugar el error cuadrático medio (discutido en la siguiente sección).
El error cuadrático medio entre sus valores esperados y predichos se puede calcular usando la función mean_squared_error () de la biblioteca scikit-learn.
La función toma una matriz unidimensional o una lista de valores esperados y valores predichos y devuelve el valor de error cuadrático medio.
|
... # calcular errores errores = error medio cuadrado(esperado, predicho) |
El siguiente ejemplo ofrece un ejemplo de cálculo del error cuadrático medio entre una lista de valores previstos y esperados artificiales.
|
# ejemplo de cálculo del error cuadrático medio desde sklearn.métrica importar mean_squared_error # valor real esperado = [[1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0] # valor predicho predicho = [[1.0, 0,9, 0.8, 0,7, 0,6, 0,5, 0.4, 0,3, 0,2, 0,1, 0.0] # calcular errores errores = error medio cuadrado(esperado, predicho) # informe de error impresión(errores) |
La ejecución del ejemplo calcula e imprime el error cuadrático medio.
Un valor de error cuadrático medio perfecto es 0.0, lo que significa que todas las predicciones coincidieron exactamente con los valores esperados.
Este casi nunca es el caso, y si sucede, sugiere que su problema de modelado predictivo es trivial.
Un buen MSE es relativo a su conjunto de datos específico.
Es una buena idea establecer primero un MSE de referencia para su conjunto de datos utilizando un modelo predictivo ingenuo, como predecir el valor objetivo medio del conjunto de datos de entrenamiento. Un modelo que logra un MSE mejor que el MSE para el modelo ingenuo tiene habilidad.
Error cuadrático medio
El error cuadrático medio, o RMSE, es una extensión del error cuadrático medio.
Es importante destacar que se calcula la raíz cuadrada del error, lo que significa que las unidades del RMSE son las mismas que las unidades originales del valor objetivo que se predice.
Por ejemplo, si su variable de destino tiene las unidades «dolares, «Entonces la puntuación de error RMSE también tendrá la unidad»dolares» y no «dólares al cuadrado”Como el MSE.
Como tal, puede ser común usar la pérdida de MSE para entrenar un modelo predictivo de regresión y usar RMSE para evaluar e informar su desempeño.
El RMSE se puede calcular de la siguiente manera:
- RMSE = sqrt (1 / N * suma de i a N (y_i – yhat_i) ^ 2)
Dónde y_i es el i-ésimo valor esperado en el conjunto de datos, yhat_i es el i-ésimo valor predicho, y sqrt () es la función raíz cuadrada.
Podemos reformular el RMSE en términos del MSE como:
Tenga en cuenta que el RMSE no se puede calcular como el promedio de la raíz cuadrada de los valores de error cuadrático medio. Este es un error común que cometen los principiantes y es un ejemplo de la desigualdad de Jensen.
Quizás recuerde que la raíz cuadrada es la inversa de la operación cuadrada. MSE usa la operación de cuadrado para eliminar el signo de cada valor de error y castigar los errores grandes. La raíz cuadrada invierte esta operación, aunque asegura que el resultado sigue siendo positivo.
La raíz del error cuadrático medio entre sus valores esperados y pronosticados se puede calcular usando la función mean_squared_error () de la biblioteca scikit-learn.
Por defecto, la función calcula el MSE, pero podemos configurarlo para calcular la raíz cuadrada del MSE configurando el “cuadrado«Argumento para Falso.
La función toma una matriz unidimensional o una lista de valores esperados y valores predichos y devuelve el valor de error cuadrático medio.
|
... # calcular errores errores = error medio cuadrado(esperado, predicho, cuadrado=Falso) |
El siguiente ejemplo ofrece un ejemplo de cálculo de la raíz del error cuadrático medio entre una lista de valores previstos y esperados artificiales.
|
# ejemplo de cálculo del error cuadrático medio desde sklearn.métrica importar mean_squared_error # valor real esperado = [[1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0] # valor predicho predicho = [[1.0, 0,9, 0.8, 0,7, 0,6, 0,5, 0.4, 0,3, 0,2, 0,1, 0.0] # calcular errores errores = error medio cuadrado(esperado, predicho, cuadrado=Falso) # informe de error impresión(errores) |
Al ejecutar el ejemplo, se calcula e imprime la raíz del error cuadrático medio.
Un valor RMSE perfecto es 0.0, lo que significa que todas las predicciones coincidieron exactamente con los valores esperados.
Este casi nunca es el caso, y si sucede, sugiere que su problema de modelado predictivo es trivial.
Un buen RMSE es relativo a su conjunto de datos específico.
Es una buena idea establecer primero un RMSE de referencia para su conjunto de datos utilizando un modelo predictivo ingenuo, como predecir el valor objetivo medio del conjunto de datos de entrenamiento. Un modelo que logra un RMSE mejor que el RMSE para el modelo ingenuo tiene habilidad.
Error absoluto medio
El error absoluto medio, o MAE, es una métrica popular porque, como RMSE, las unidades de la puntuación de error coinciden con las unidades del valor objetivo que se predice.
A diferencia de RMSE, los cambios en RMSE son lineales y, por lo tanto, intuitivos.
Es decir, MSE y RMSE castigan los errores más grandes que los errores más pequeños, inflando o magnificando la puntuación de error media. Esto se debe al cuadrado del valor de error. El MAE no da más o menos peso a los diferentes tipos de errores y, en cambio, las puntuaciones aumentan linealmente con los aumentos del error.
Como sugiere su nombre, la puntuación MAE se calcula como el promedio de los valores de error absoluto. Absoluto o abdominales() es una función matemática que simplemente hace que un número sea positivo. Por lo tanto, la diferencia entre un valor esperado y predicho puede ser positiva o negativa y está obligada a ser positiva al calcular el MAE.
El MAE se puede calcular de la siguiente manera:
- MAE = 1 / N * suma para i a N abs (y_i – yhat_i)
Dónde y_i es el i-ésimo valor esperado en el conjunto de datos, yhat_i es el i-ésimo valor predicho y abdominales() es la función absoluta.
Podemos crear una gráfica para tener una idea de cómo el cambio en el error de predicción impacta en el MAE.
El siguiente ejemplo proporciona un pequeño conjunto de datos artificial de todos los valores 1.0 y predicciones que van desde perfecto (1.0) a incorrecto (0.0) en incrementos de 0.1. El error absoluto entre cada predicción y el valor esperado se calcula y se traza para mostrar el aumento lineal del error.
|
... # calcular error errar = abdominales((esperado[[yo] – predicho[[yo])) |
El ejemplo completo se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 |
# gráfico del aumento del error absoluto medio con error de predicción desde matplotlib importar pyplot desde sklearn.métrica importar mean_squared_error # valor real esperado = [[1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0] # valor predicho predicho = [[1.0, 0,9, 0.8, 0,7, 0,6, 0,5, 0.4, 0,3, 0,2, 0,1, 0.0] # calcular errores errores = lista() para yo en rango(len(esperado)): # calcular error errar = abdominales((esperado[[yo] – predicho[[yo])) # error de tienda errores.adjuntar(errar) # informe de error impresión(‘>%. 1f,% .1f =% .3f’ % (esperado[[yo], predicho[[yo], errar)) # errores de trazado pyplot.trama(errores) pyplot.xticks(garrapatas=[[yo para yo en rango(len(errores))], etiquetas=predicho) pyplot.xlabel(‘Valor previsto’) pyplot.etiquetarse(‘Error absoluto medio’) pyplot.show() |
La ejecución del ejemplo primero informa el valor esperado, el valor predicho y el error absoluto para cada caso.
Podemos ver que el error aumenta linealmente, lo que es intuitivo y fácil de entender.
|
> 1.0, 1.0 = 0.000 > 1.0, 0.9 = 0.100 > 1.0, 0.8 = 0.200 > 1.0, 0.7 = 0.300 > 1.0, 0.6 = 0.400 > 1.0, 0.5 = 0.500 > 1.0, 0.4 = 0.600 > 1.0, 0.3 = 0.700 > 1.0, 0.2 = 0.800 > 1.0, 0.1 = 0.900 > 1.0, 0.0 = 1.000 |
Se crea un gráfico de líneas que muestra el aumento lineal o en línea recta en el valor del error absoluto a medida que aumenta la diferencia entre el valor esperado y el predicho.
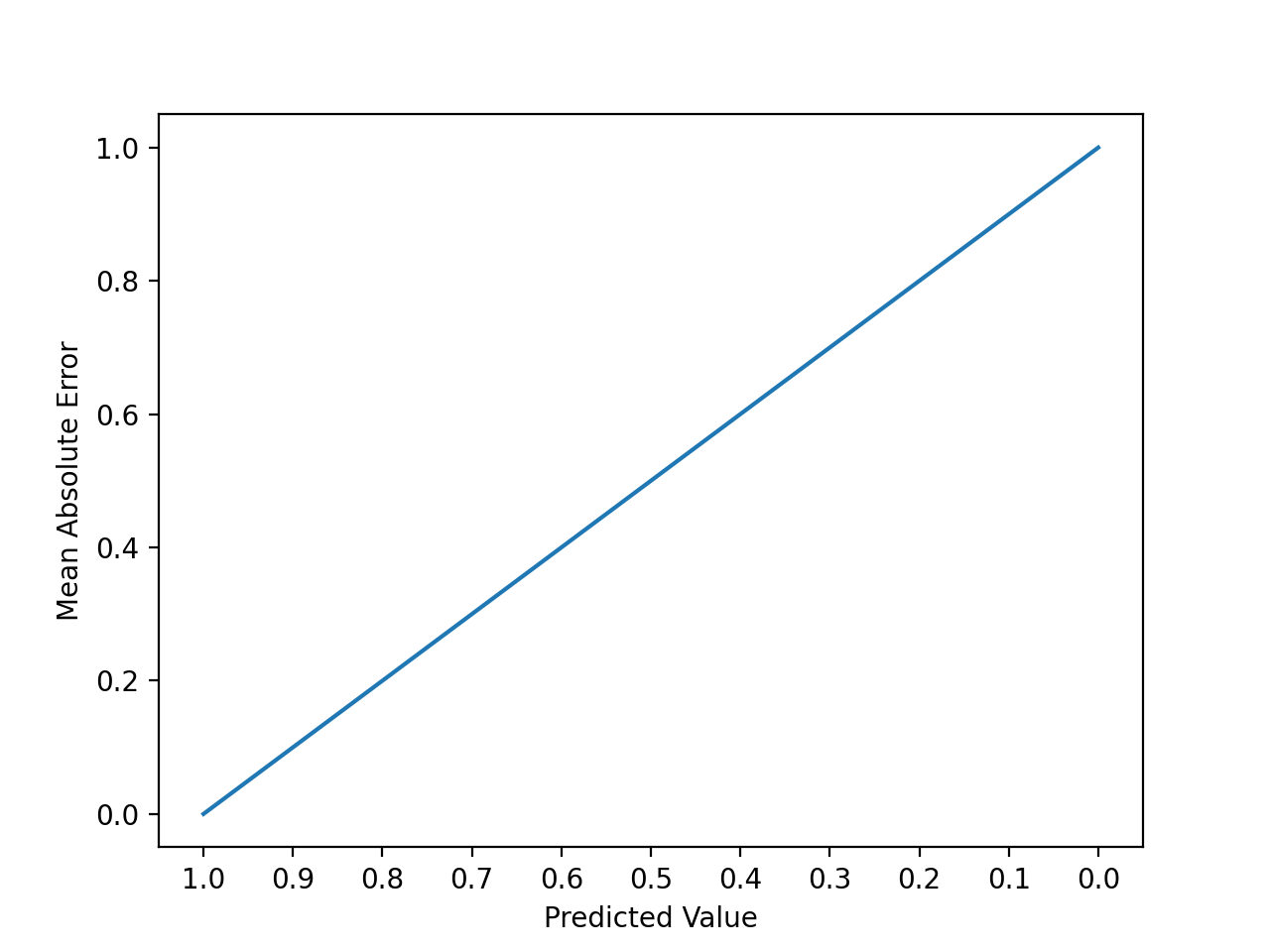
Gráfica lineal del aumento del error absoluto con predicciones
El error absoluto medio entre sus valores esperados y predichos se puede calcular usando la función mean_absolute_error () de la biblioteca scikit-learn.
La función toma una matriz unidimensional o una lista de valores esperados y valores predichos y devuelve el valor de error absoluto medio.
|
... # calcular errores errores = mean_absolute_error(esperado, predicho) |
El siguiente ejemplo ofrece un ejemplo de cómo calcular el error absoluto medio entre una lista de valores previstos y esperados artificiales.
|
# ejemplo de cálculo del error absoluto medio desde sklearn.métrica importar mean_absolute_error # valor real esperado = [[1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0] # valor predicho predicho = [[1.0, 0,9, 0.8, 0,7, 0,6, 0,5, 0.4, 0,3, 0,2, 0,1, 0.0] # calcular errores errores = mean_absolute_error(esperado, predicho) # informe de error impresión(errores) |
La ejecución del ejemplo calcula e imprime el error absoluto medio.
Un valor de error absoluto medio perfecto es 0.0, lo que significa que todas las predicciones coincidieron exactamente con los valores esperados.
Este casi nunca es el caso, y si sucede, sugiere que su problema de modelado predictivo es trivial.
Un buen MAE es relativo a su conjunto de datos específico.
Es una buena idea establecer primero un MAE de línea base para su conjunto de datos utilizando un modelo predictivo ingenuo, como predecir el valor objetivo medio del conjunto de datos de entrenamiento. Un modelo que logra un MAE mejor que el MAE para el modelo ingenuo tiene habilidad.
Otras lecturas
Esta sección proporciona más recursos sobre el tema si está buscando profundizar.
Tutoriales
API
Artículos
Resumen
En este tutorial, descubrió cómo calcular el error para proyectos de modelado predictivo de regresión.
Específicamente, aprendiste:
- Los modelos predictivos de regresión son aquellos problemas que involucran la predicción de un valor numérico.
- Las métricas para la regresión implican calcular una puntuación de error para resumir la habilidad predictiva de un modelo.
- Cómo calcular y reportar el error cuadrático medio, el error cuadrático medio y el error absoluto medio.
¿Tiene usted alguna pregunta?
Haga sus preguntas en los comentarios a continuación y haré todo lo posible para responder.

