La regla de la cadena de cálculo para funciones univariadas y multivariadas

La regla de la cadena nos permite encontrar la derivada de funciones compuestas.

Se calcula ampliamente mediante el algoritmo de retropropagación, con el fin de entrenar redes neuronales de retroalimentación. Aplicando la regla de la cadena de manera eficiente mientras sigue un orden específico de operaciones, el algoritmo de retropropagación calcula el gradiente de error de la función de pérdida con respecto a cada peso de la red.

En este tutorial, descubrirá la regla de la cadena de cálculo para funciones univariadas y multivariadas.

Después de completar este tutorial, sabrá:

• Una función compuesta es la combinación de dos (o más) funciones.
• La regla de la cadena nos permite encontrar la derivada de una función compuesta.
• La regla de la cadena se puede generalizar a funciones multivariadas y se puede representar mediante un diagrama de árbol.
• La regla de la cadena se aplica ampliamente mediante el algoritmo de retropropagación para calcular el gradiente de error de la función de pérdida con respecto a cada peso.

Empecemos.

La regla de la cadena de cálculo para funciones univariadas y multivariadas
Foto de Pascal Debrunner, algunos derechos reservados.

Descripción general del tutorial

Este tutorial se divide en cuatro partes; ellos son:

• Funciones compuestas
• La regla de la cadena
• La regla de la cadena generalizada
• Aplicación en aprendizaje automático

Prerrequisitos

Para este tutorial, asumimos que ya sabe cuáles son:

Puede revisar estos conceptos haciendo clic en los enlaces que se muestran arriba.

Funciones compuestas

Hasta ahora, hemos cumplido funciones de variables únicas y múltiples (llamadas, univariado y multivariado funciones, respectivamente). Ahora extenderemos ambos a su compuesto formas. Eventualmente, veremos cómo aplicar la regla de la cadena para encontrar su derivada, pero más sobre esto en breve.

Una función compuesta es la combinación de dos funciones.

– Página 49, Cálculo para tontos, 2016.

Considere dos funciones de una sola variable independiente, F(X) = 2X – 1 y gramo(X) = X³. Su función compuesta se puede definir de la siguiente manera:

h = gramo(F(X))

En esta operación, gramo es una función de F. Esto significa que gramo se aplica al resultado de aplicar la función, F, para X, produciendo h.

Consideremos un ejemplo concreto usando las funciones especificadas anteriormente para entender esto mejor.

Suponer que F(X) y gramo(X) son dos sistemas en cascada, que reciben una entrada X = 5:

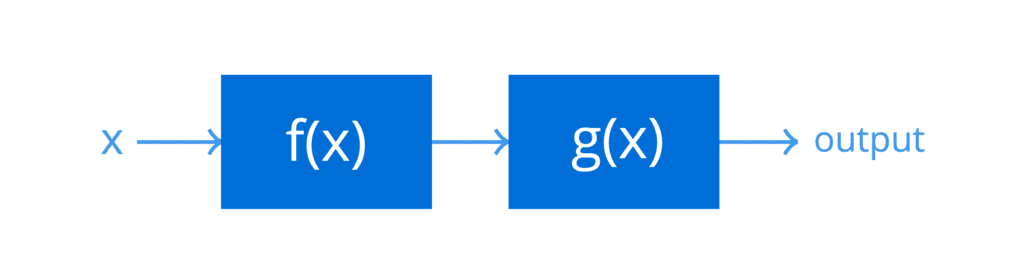
Dos sistemas en cascada que representan una función compuesta

Ya que F(X) es el primer sistema en la cascada (porque es la función interna en el compuesto), su salida se resuelve primero:

F(5) = (2 × 5) – 1 = 9

Este resultado luego se transmite como entrada a gramo(X), el segundo sistema en la cascada (porque es la función externa en el compuesto) para producir el resultado neto de la función compuesta:

gramo(9) = 9³ = 729

Alternativamente, podríamos haber calculado el resultado neto de una sola vez, si hubiéramos realizado el siguiente cálculo:

h = gramo(F(X)) = (2X – 1)³ = 729

La composición de funciones también se puede considerar como un encadenamiento proceso, para usar un término más familiar, donde la salida de una función alimenta a la siguiente en la cadena.

Con funciones compuestas, el orden importa.

– Página 49, Cálculo para tontos, 2016.

Tenga en cuenta que la composición de funciones es una no conmutativo proceso, lo que significa que cambiar el orden de F(X) y gramo(X) en la cascada (o cadena) no produce los mismos resultados. Por eso:

gramo(F(X)) ≠ F(gramo(X))

La composición de funciones también se puede extender al caso multivariado:

h = gramo(r, s, t) = gramo(r(x, y), s(x, y), t(x, y)) = gramo(F(x, y))

Aquí, F(x, y) es una función con valores vectoriales de dos variables independientes (o entradas), X y y. Se compone de tres componentes (para este ejemplo en particular) que son r(x, y), s(x, y) y t(x, y), y que también se conocen como componente funciones de F.

Esto significa que F(X, y) asignará dos entradas a tres salidas, y luego alimentará estas tres salidas al sistema consecutivo en la cadena, gramo(r, s, t), para producir h.

La regla de la cadena

La regla de la cadena nos permite encontrar la derivada de una función compuesta.

Primero definamos cómo la regla de la cadena diferencia una función compuesta y luego dividámosla en sus componentes separados para comprenderla mejor. Si tuviéramos que considerar nuevamente la función compuesta, h = gramo(F(X)), entonces su derivada dada por la regla de la cadena es:

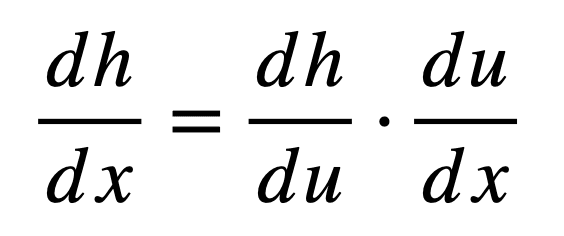
Aquí, tu es la salida de la función interna F (por eso, tu = F(X)), que luego se alimenta como entrada a la siguiente función gramo para producir h (por eso, h = gramo(tu)). Observe, por lo tanto, cómo la regla de la cadena relaciona la producción neta, h, a la entrada, X, a través de un variable intermedia, tu.

Recuerde que la función compuesta se define de la siguiente manera:

h(X) = gramo(F(X)) = (2X – 1)³

El primer componente de la regla de la cadena, dh / du, nos dice que comencemos por encontrar la derivada de la parte externa de la función compuesta, mientras ignoramos lo que está adentro. Para ello aplicaremos la regla de la potencia:

((2X – 1)³) ‘= 3 (2X – 1)²

Luego, el resultado se multiplica al segundo componente de la regla de la cadena, du / dx, que es la derivada de la parte interna de la función compuesta, esta vez ignorando lo que está afuera:

((2X – 1) ‘)³ = 2

La derivada de la función compuesta definida por la regla de la cadena es, entonces, la siguiente:

h‘= 3 (2X – 1)² × 2 = 6 (2X – 1)²

Por este medio, hemos considerado un ejemplo simple, pero el concepto de aplicar la regla de la cadena a funciones más complicadas sigue siendo el mismo. Consideraremos funciones más desafiantes en un tutorial separado.

La regla de la cadena generalizada

Podemos generalizar la regla de la cadena más allá del caso univariante.

Considere el caso donde X ∈ ℝ^metro y tu ∈ ℝ^norte, lo que significa que la función interna, F, mapas metro entradas a norte salidas, mientras que la función exterior, gramo, recibe norte insumos para producir una salida, h. Para I = 1,…, metro la regla de la cadena generalizada establece:

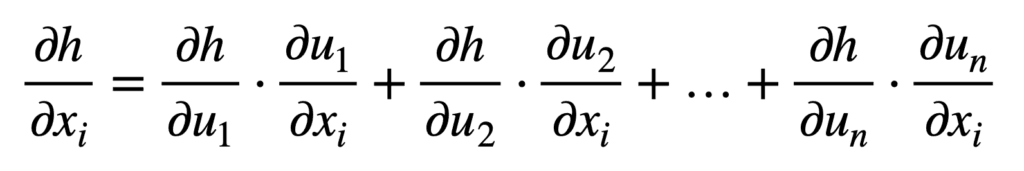
O en su forma más compacta, para j = 1,…, norte:

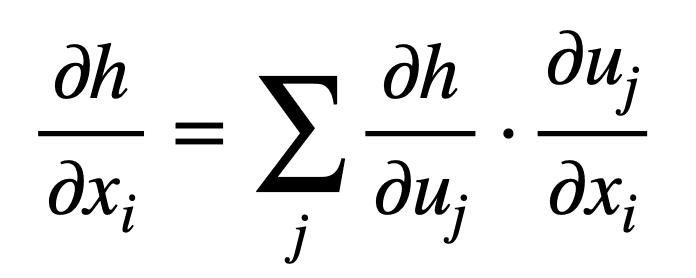
Recuerde que empleamos el uso de derivadas parciales cuando encontramos el gradiente de una función de múltiples variables.

También podemos visualizar el funcionamiento de la regla de la cadena mediante un diagrama de árbol.

Supongamos que tenemos una función compuesta de dos variables independientes, X₁ y X₂, definido como sigue:

h = gramo(F(X₁, X₂)) = gramo(tu₁(X₁, X₂), tu₂(X₁, X₂))

Aquí, tu₁ y tu₂ actúan como las variables intermedias. Su diagrama de árbol se representaría de la siguiente manera:

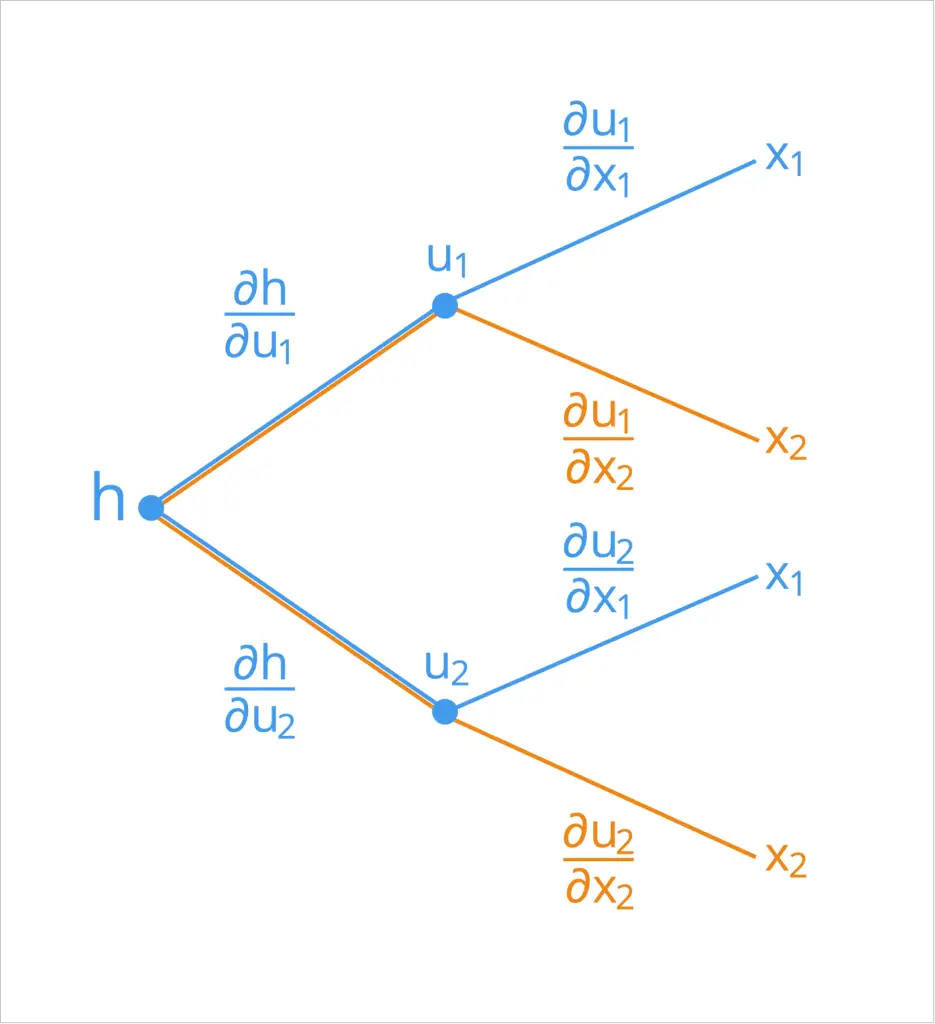
Representar la regla de la cadena mediante un diagrama de árbol

Para derivar la fórmula para cada una de las entradas, X₁ y X₂, podemos comenzar desde el lado izquierdo del diagrama de árbol y seguir sus ramas hacia la derecha. De esta manera, encontramos que formamos las siguientes dos fórmulas (las ramas que se resumen han sido codificadas por colores para simplificar):

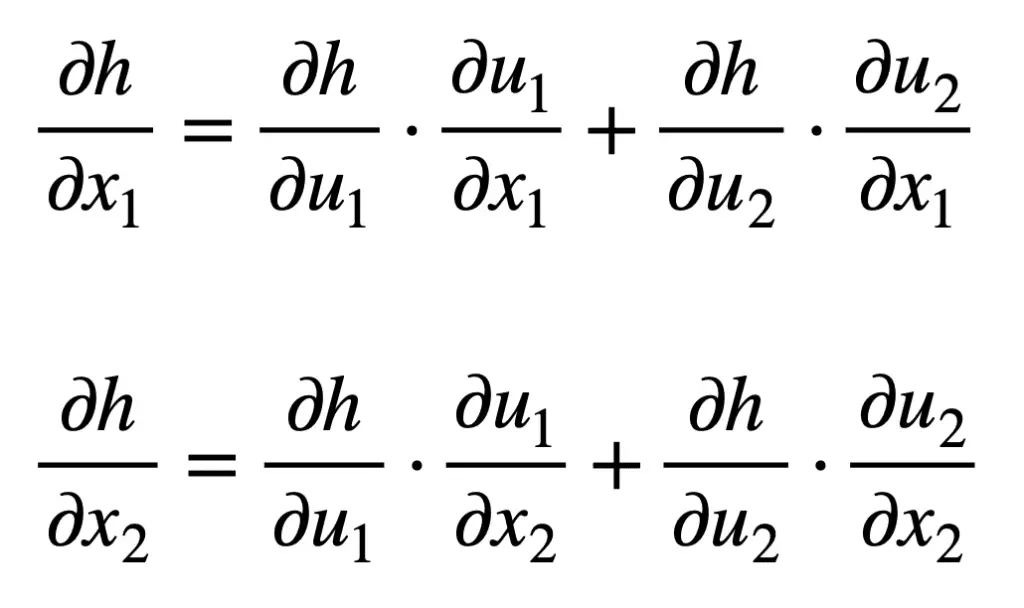
Observe cómo la regla de la cadena relaciona la producción neta, h, a cada una de las entradas, X_I, a través de las variables intermedias, tu_j. Este es un concepto que el algoritmo de retropropagación aplica ampliamente para optimizar los pesos de una red neuronal.

Aplicación en aprendizaje automático

Observe lo similar que es el diagrama de árbol a la representación típica de una red neuronal (aunque generalmente representamos esta última colocando las entradas en el lado izquierdo y las salidas en el lado derecho). Podemos aplicar la regla de la cadena a una red neuronal mediante el uso del algoritmo de retropropagación, de una manera muy similar a como la hemos aplicado al diagrama de árbol anterior.

Un área donde la regla de la cadena se usa al extremo es el aprendizaje profundo, donde el valor de la función y se calcula como una composición de funciones de muchos niveles.

– Página 159, Matemáticas para el aprendizaje automático, 2020.

De hecho, una red neuronal puede representarse mediante una función compuesta anidada masiva. Por ejemplo:

y = F_K ( F_{K – 1} (… ( F₁(X))…))

Aquí, X son las entradas a la red neuronal (por ejemplo, las imágenes) mientras que y son las salidas (por ejemplo, las etiquetas de clase). Cada función F_I, por I = 1,…, K, se caracteriza por sus propios pesos.

La aplicación de la regla de la cadena a dicha función compuesta nos permite trabajar hacia atrás a través de todas las capas ocultas que componen la red neuronal y calcular de manera eficiente el gradiente de error de la función de pérdida con respecto a cada peso. w_I, de la red hasta llegar a la entrada.

Otras lecturas

Esta sección proporciona más recursos sobre el tema si desea profundizar.

Libros

Resumen

En este tutorial, descubrió la regla de la cadena del cálculo para funciones univariadas y multivariadas.

Específicamente, aprendiste:

• Una función compuesta es la combinación de dos (o más) funciones.
• La regla de la cadena nos permite encontrar la derivada de una función compuesta.
• La regla de la cadena se puede generalizar a funciones multivariadas y se puede representar mediante un diagrama de árbol.
• La regla de la cadena se aplica ampliamente mediante el algoritmo de retropropagación para calcular el gradiente de error de la función de pérdida con respecto a cada peso.

¿Tiene usted alguna pregunta?
Haga sus preguntas en los comentarios a continuación y haré todo lo posible para responder.