Casi todas las aplicaciones del aprendizaje por refuerzo en el mundo real implican algún grado de cambio entre el entorno de formación y el entorno de prueba. Sin embargo, trabajos anteriores han observado que incluso pequeños cambios en el entorno hacen que la mayoría de los algoritmos de RL funcionen notablemente peor.
Dado que nuestro objetivo es escalar los algoritmos de aprendizaje por refuerzo y aplicarlos en el mundo real, es cada vez más importante aprender políticas que sean robustas a los cambios en el entorno.
Aprendizaje por refuerzo robusto maximiza la recompensa en un entorno elegido por el adversario.
En términos generales, los enfoques anteriores para manejar el cambio de distribución en RL tienen como objetivo maximizar el rendimiento en el caso promedio o en el peor de los casos. El primer conjunto de enfoques, como la aleatorización de dominios, entrena una política en una distribución de entornos y optimiza el rendimiento promedio de la política en estos entornos. Si bien estos métodos se han aplicado con éxito a varias áreas
(por ejemplo, coches autónomos, locomoción y manipulación robóticas),
su éxito se basa fundamentalmente en el diseño de la distribución de entornos.
Además, no se garantiza que las políticas que obtienen buenos resultados en promedio obtengan una gran recompensa en todos los entornos. La política que obtiene la recompensa más alta en promedio puede obtener una recompensa muy baja en una pequeña fracción de entornos. El segundo conjunto de enfoques, normalmente denominado robusto RL, céntrese en los peores escenarios. El objetivo es encontrar una política que obtenga una gran recompensa en todos los entornos dentro de algún conjunto. El RL robusto se puede considerar de manera equivalente como un juego de dos jugadores entre la política y un adversario ambiental. La política intenta obtener una alta recompensa, mientras que el adversario del medio ambiente intenta modificar la dinámica y la función de recompensa del medio ambiente para que la política obtenga una recompensa menor. Una propiedad importante del enfoque robusto es que, a diferencia de la aleatorización de dominios, es invariante a la proporción de tareas fáciles y difíciles. Mientras que el RL robusto siempre evalúa una política en las tareas más desafiantes, la aleatorización de dominios predecirá que la política es mejor si se evalúa en una distribución de entornos con tareas más fáciles.
El trabajo anterior ha sugerido una serie de algoritmos para resolver problemas sólidos de RL. En general, todos estos algoritmos siguen la misma receta: tome un algoritmo RL existente y agregue algo de maquinaria adicional en la parte superior para hacerlo robusto.
Por ejemplo, la iteración de valor robusto utiliza Q-learning como el algoritmo de RL base y modifica la actualización de Bellman resolviendo un problema de optimización convexa en el bucle interno de cada copia de seguridad de Bellman.
De manera similar, Pinto ’17 usa TRPO como el algoritmo de RL base y actualiza periódicamente el entorno en función del comportamiento de la política actual. Estos enfoques anteriores a menudo son difíciles de implementar e, incluso una vez implementados correctamente, requieren el ajuste de muchos hiperparámetros adicionales. ¿Podría haber un enfoque más simple, un enfoque que no requiera hiperparámetros adicionales y líneas de código adicionales para depurar?
Para responder a esta pregunta, nos centraremos en un tipo de algoritmo RL conocido como RL de máxima entropía, o MaxEnt RL para abreviar (Todorov ’06, Rawlik ’08, Ziebart ’10).
MaxEnt RL es una ligera variante de RL estándar que tiene como objetivo aprender una política que obtenga una alta recompensa mientras actúa de la manera más aleatoria posible; formalmente, MaxEnt maximiza la entropía de la política. Algunos trabajos anteriores han observado empíricamente que los algoritmos MaxEnt RL parecen ser robustos a algunas perturbaciones del medio ambiente.
Hasta donde sabemos, ningún trabajo previo ha probado realmente que MaxEnt RL sea resistente a las perturbaciones ambientales.
En un artículo reciente, demostramos que cada problema de MaxEnt RL corresponde a maximizar un límite inferior en un problema de RL robusto. Por lo tanto, cuando ejecuta MaxEnt RL, está resolviendo implícitamente un problema de RL sólido. Nuestro análisis proporciona una explicación teóricamente justificada de la solidez empírica de MaxEnt RL y demuestra que MaxEnt RL es en sí mismo un algoritmo RL robusto.
En el resto de esta publicación, proporcionaremos algo de intuición sobre por qué MaxEnt RL debería ser robusto y a qué tipo de perturbaciones es robusto MaxEnt RL. También mostraremos algunos experimentos que demuestran la solidez de MaxEnt RL.
Entonces, ¿por qué esperaríamos que MaxEnt RL fuera resistente a las perturbaciones en el medio ambiente? Recuerde que MaxEnt RL entrena políticas no solo para maximizar la recompensa, sino para hacerlo actuando de la manera más aleatoria posible. En esencia, la política en sí está inyectando tanto ruido como sea posible en el medio ambiente, por lo que se pone a “practicar” recuperarse de las perturbaciones. Por lo tanto, si el cambio en la dinámica parece simplemente una perturbación en el entorno original, nuestra política ya ha sido entrenada con esos datos. Otra forma de ver MaxEnt RL es aprender muchas formas diferentes de resolver la tarea (Kappen ’05). Por ejemplo, veamos la tarea que se muestra en los videos a continuación: queremos que el robot empuje el objeto blanco hacia la región verde. Los dos videos principales muestran que el RL estándar siempre toma el camino más corto hacia la meta, mientras que MaxEnt RL toma muchos caminos diferentes hacia la meta. Ahora, imaginemos que agregamos un nuevo obstáculo (bloques rojos) que no se incluyó durante el entrenamiento. Como se muestra en los videos en la fila inferior, la política aprendida por el estándar RL casi siempre choca con el obstáculo y rara vez alcanza la meta. Por el contrario, la política de MaxEnt RL a menudo elige rutas alrededor del obstáculo y continúa alcanzando la meta en una gran parte de las pruebas.
|
RL estándar |
MaxEnt RL |
|
|
Entrenado y evaluado sin el obstáculo: |
 |
 |
|
Entrenado sin el obstáculo, pero evaluado con |
 |
 |
Ahora describimos formalmente los resultados técnicos del documento. El objetivo aquí no es proporcionar una prueba completa (ver el Apéndice en papel para eso), sino construir algo de intuición sobre lo que dicen los resultados técnicos. Nuestro principal resultado es que, cuando aplica MaxEnt RL con alguna función de recompensa y cierta dinámica, en realidad está maximizando un límite inferior en el objetivo RL robusto. Para explicar este resultado, primero debemos definir el objetivo MaxEnt RL:
$ J_ {MaxEnt} ( pi; p, r) $ es el rendimiento acumulativo regularizado entropía de la política $ pi $ cuando se evalúa usando la dinámica $ p (s ‘ mid s, a) $ y la función de recompensa $ r (s , a) $. Si bien entrenaremos la política usando una dinámica $ p $, evaluaremos la política en una dinámica diferente, $ tilde {p} (s ’ mid s, a) $, elegida por el adversario. Ahora podemos establecer formalmente nuestro resultado principal de la siguiente manera:
El lado izquierdo es el objetivo RL robusto. Dice que el adversario se
para elegir cualquier función dinámica $ tilde {p} (s ’ mid s, a) $ hace que nuestra política funcione tan mal como
posible, sujeto a algunas restricciones (según lo especificado por el conjunto $ tilde { mathcal {P}} $). En
el lado derecho tenemos el objetivo MaxEnt RL (tenga en cuenta que $ log T $ es un
constante, y la función $ exp ( cdots) $ siempre está aumentando). Por tanto, este objetivo
dice que una política que tiene una recompensa regularizada de alta entropía (lado derecho)
También se garantiza que obtendrá una alta recompensa cuando se evalúe en un grupo elegido por el adversario.
dinámica.
La parte más importante de esta ecuación es el conjunto $ tilde { mathcal {P}} $ de dinámica que
el adversario puede elegir. Nuestro análisis describe precisamente cómo este conjunto es
construido y muestra que, si queremos que una política sea robusta a un conjunto mayor de
perturbaciones, todo lo que tenemos que hacer es aumentar el peso en el término de entropía y
disminuir el peso en el plazo de recompensa. Intuitivamente, el adversario debe elegir
dinámicas que están “próximas” a las dinámicas sobre las que se formó la política. Para
ejemplo, en el caso especial donde la dinámica es lineal-gaussiana, este conjunto
corresponde a todas las perturbaciones donde el siguiente estado original esperado y el
el próximo estado esperado perturbado tiene una distancia euclidiana menor que $ epsilon $.
Nuestro análisis predice que MaxEnt RL debería ser robusto para muchos tipos de
disturbios. El primer conjunto de videos en esta publicación mostró que MaxEnt RL es robusto para
obstáculos estáticos. MaxEnt RL también es resistente a las perturbaciones dinámicas introducidas en el
en medio de un episodio. Para demostrar esto, tomamos la misma tarea de empuje robótico
y sacó el disco de su lugar en medio del episodio. Los videos a continuación
muestran que la política aprendida por MaxEnt RL es más sólida en el manejo de estos
perturbaciones, como predice nuestro análisis.
|
RL estándar |
MaxEnt RL |
 |
 |
La política aprendida por MaxEntRL es robusta a las perturbaciones dinámicas del disco (marcos rojos).
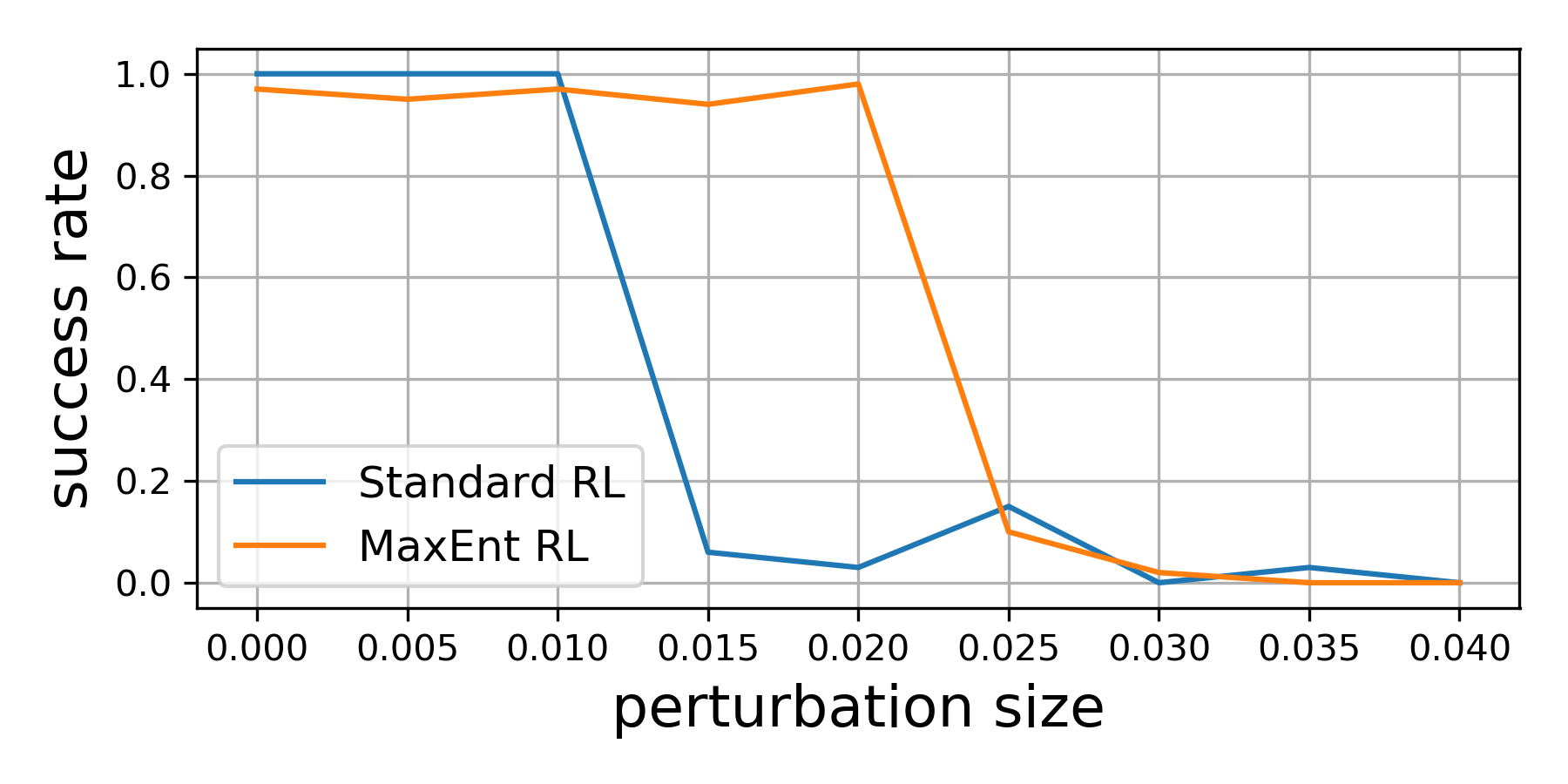
Nuestros resultados teóricos sugieren que, incluso si optimizamos el entorno
perturbaciones para que el agente lo haga lo peor posible, las pólizas MaxEnt RL
aún ser robusto. Para demostrar esta capacidad, capacitamos tanto a RL estándar como a
MaxEnt RL en una tarea de inserción de clavijas que se muestra a continuación. Durante la evaluación, cambiamos el
posición del agujero para intentar que cada política falle. Si solo moviéramos el agujero
posición un poco ($ le $ 1 cm), ambas políticas siempre resolvieron la tarea. Sin embargo,
si movimos la posición del agujero hasta 2 cm, la política aprendida por RL estándar
casi nunca logró insertar la clavija, mientras que la política MaxEnt RL
tuvo éxito en el 95% de los ensayos. Este experimento valida nuestra
hallazgos teóricos de que MaxEnt realmente es robusto ante adversarios (limitados)
perturbaciones en el medio ambiente.
 |
 |
 |
|
RL estándar |
MaxEnt RL |
Evaluación de perturbaciones adversas |
MaxEnt RL es resistente a las perturbaciones adversas del agujero (donde el robot
inserta la clavija).
En resumen, nuestro artículo muestra que un tipo de algoritmo RL de uso común, MaxEnt
RL, ya está resolviendo un problema de RL robusto. No afirmamos que MaxEnt RL
superan a los robustos algoritmos RL diseñados específicamente. Sin embargo, el sorprendente
La simplicidad de MaxEnt RL en comparación con otros algoritmos robustos de RL sugiere que
puede ser una alternativa atractiva para los profesionales que esperan equipar su RL
políticas con una pizca de solidez.
Agradecimientos
Gracias a Gokul Swamy, Diba Ghosh, Colin Li y Sergey Levine por sus comentarios sobre los borradores de esta publicación,
ya Chloe Hsu y Daniel Seita por su ayuda con el blog.
Esta publicación se basa en el siguiente documento:
