La Ley de Goodhart es un adagio que dice lo siguiente:
«Cuando una medida se convierte en un objetivo, deja de ser una buena medida».
Esto es particularmente pertinente en el aprendizaje por máquina, donde la fuente de muchas de las
nuestros mayores logros provienen de la optimización de un objetivo en forma de una pérdida
función. La forma más prominente de hacerlo es con el descenso de gradiente estocástico
(SGD), que aplica una simple regla, sigue el gradiente:
Por un tamaño de escalón $\N-alfa$. Las actualizaciones de este formulario han llevado a una serie de
avances desde la visión por ordenador hasta el aprendizaje de refuerzo, y es fácil
ver por qué es tan popular: 1) es relativamente barato para calcular usando el backprop
2) se garantiza la reducción local de la pérdida en cada paso y finalmente 3) se
tiene un increíble historial empírico.
Sin embargo, no estaríamos escribiendo esto si el SGD fuera perfecto. De hecho, hay algunos
Negativos. Lo más importante es que hay un sesgo intrínseco hacia lo «fácil
soluciones (típicamente asociadas con una alta curvatura negativa). En algunos casos,
dos soluciones con la misma pérdida pueden ser cualitativamente diferentes, y si una es
más fácil de encontrar entonces es probable que sea la única solución encontrada por SGD. Esto tiene
recientemente se ha denominado solución «abreviada». [1], ejemplos de los cuales son
abajo:
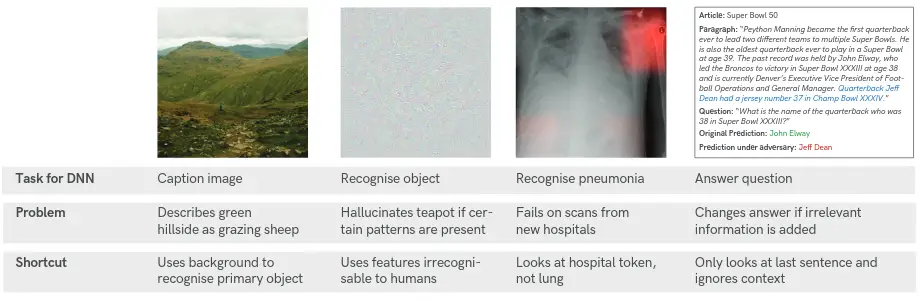
Como vemos, al clasificar las ovejas, la red aprende a utilizar el verde
antecedentes para identificar las ovejas presentes. Cuando en cambio se le proporciona un
imagen de ovejas en una playa (lo cual es una perspectiva interesante) entonces falla
por completo. Por lo tanto, la pregunta clave que motiva nuestro trabajo es la siguiente:
Pregunta: ¿Cómo podemos encontrar un conjunto diverso de soluciones diferentes?
Nuestra respuesta a esto es seguir los vectores propios del Hesse (‘crestas’) con
valores propios negativos de una silla de montar, en lo que llamamos Ridge Rider (RR).
Hay mucho que desempacar en esa declaración, así que entraremos en más detalles en
la siguiente sección.
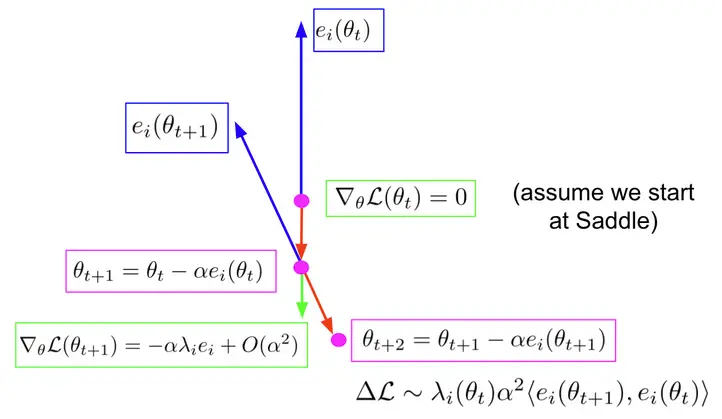
Primero, asumimos que empezamos en una silla de montar (verde), donde la norma del gradiente
es cero. Calculamos los eigenvectores y eigenvalores del Hessian, que
resolver lo siguiente:
Y seguimos los eigenvectores con valores propios negativos, que llamamos crestas.
Podemos seguirlos en ambas direcciones. Como ves en el diagrama, cuando tomamos
un paso a lo largo de la cresta (en rojo) llegamos a un nuevo punto. Ahora el gradiente es el
tamaño del paso multiplicado por el valor propio y el vector propio, porque el
eigenvector era de los hessianos. Ahora volvemos a calcular el espectro, y seleccionamos el
nueva cresta como la que tiene el mayor producto interno con la anterior, para
preservar la dirección. Luego damos un paso a lo largo de una nueva cresta, para
$theta_{t+2}$.
Entonces, ¿por qué hacemos esto? Bueno, en el periódico mostramos que si el interior
entre la nueva y la vieja cresta es mayor que cero, entonces estamos
teóricamente garantizado para mejorar nuestra pérdida. Lo que esto significa es que RR proporciona
nosotros con un conjunto ortogonal de direcciones de reducción de pérdidas. Esto se opone a
SGD, que casi siempre seguirá a uno solo.
En el siguiente diagrama mostramos el algoritmo completo de Ridge Rider.

Comenzamos con una silla de montar de máxima invariabilidad (MIS) que retiene y respeta todos los
las simetrías del problema subyacente. Nos ramificamos, y seleccionamos una cresta para
que actualizamos hasta llegar a un punto de ruptura donde nos ramificamos de nuevo.
En este punto podemos elegir entre continuar por el camino actual o
seleccione otra cresta del buffer. Esto equivale a elegir entre
amplitud primera búsqueda de profundidad primera búsqueda. Finalmente las hojas del árbol son
las soluciones a nuestro problema, cada una de ellas está definida de manera única por la huella dactilar.
En el lado positivo, el RR nos proporciona un conjunto de ortogonales localmente
direcciones de reducción de pérdidas que pueden ser usadas para abarcar un árbol de soluciones. Se
esencialmente convierte la optimización en un problema de búsqueda, lo que nos permite
introducir nuevos métodos a utilizar para encontrar soluciones. También nos beneficiamos de la
esquema de ordenamiento y agrupamiento natural proporcionado por los valores propios (Huella digital).
Sin embargo, por supuesto, hay muchas preguntas obvias que surgen naturalmente con
este enfoque. Aquí intentamos responder a las preguntas frecuentes:
Q: ¡Esto parece caro! ¿No necesita muchas muestras debido a la alta variabilidad del Hessian?
R: ¡Sí, eso es justo!
Q: ¡Esto parece caro! ¿Necesita reevaluar el espectro completo del Hessian en cada paso temporal?
R: ¡En realidad no! Presentamos una versión aproximada del RR usando el Vector Hessian
Productos. Vamos a entrar en esto a continuación.
Usamos el método Power/Lanczos en GetRidges. En UpdateRidge, después de cada paso
a lo largo de la cresta, encontramos el nuevo par $e_i, lambda_i$ minimizando:
Comenzamos con la aproximación de primer orden a $lambda(|theta)$, donde
$theta’, ~ -lambda’, e_i’$ son los valores anteriores:
¡Estos términos sólo se basan en los productos vectoriales de Hesse!
Q: ¡Esto parece caro! ¿No necesita evaluar cientos o miles de ramas?
R: En realidad no lo hacemos. Mostramos en el periódico que las simetrías conducen a repetidas
Valores propios, lo que reduce el número de ramas que necesitamos explorar.
Una simetría, $phi$, de la función de pérdida es una bijección en el parámetro
espacio de tal manera que
Mostramos que en presencia de simetrías, el hessiano ha repetido
eigenvalores. ¡Esto significa que sólo tenemos que explorar uno de cada conjunto!
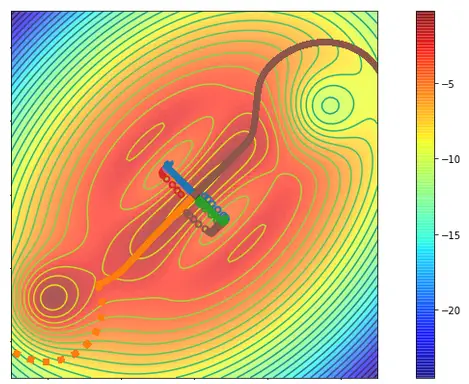
La figura de arriba muestra una superficie de coste 2d, donde empezamos en el medio y queremos
para llegar a las zonas azules. El SGD siempre se queda atascado en los valles que corresponden
a la dirección de descenso más empinada localmente, esto se muestra con los círculos. Cuando
corriendo RR, la primera cresta también sigue esta dirección, como vemos en azul y
verde. Sin embargo, la segunda, la dirección ortogonal (marrón y naranja) evita la
local y llega a las regiones de alto valor.
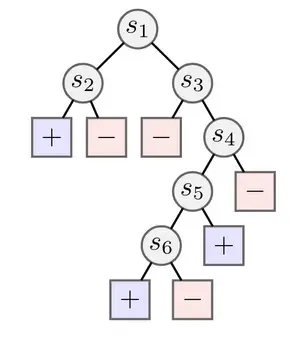
Probamos el RR en el entorno tabular de RL, donde buscamos encontrar diversos
soluciones a una tarea de exploración de árboles. Generamos árboles como el
arriba, que tiene recompensas positivas o negativas en las hojas. En este caso
ver que es mucho más fácil encontrar la recompensa positiva a la izquierda, correspondiente a
una póliza que va a la izquierda a $s_1$ y a la izquierda a $s_2$. Para encontrar la solución en
la parte inferior (yendo a la izquierda de $s_6$) requiere evitar varias recompensas negativas.
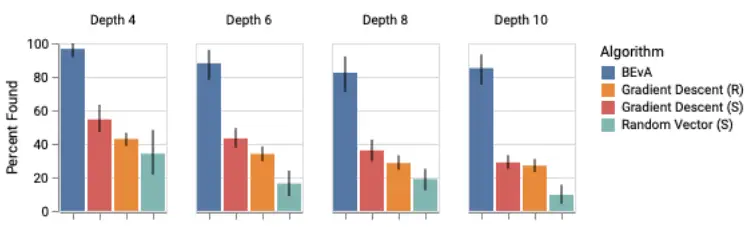
Para evaluar rigurosamente el RR, generamos 20 árboles para cuatro profundidades diferentes, y
corrió el algoritmo cada vez, comparando con el Descenso de Gradiente a partir de
inicializaciones aleatorias o el MIS, y vectores aleatorios del MIS. Los resultados
muestran que el RR en promedio encuentra casi todas las soluciones, mientras que los otros métodos
…ni siquiera encuentran la mitad.
En el documento incluimos ablaciones adicionales, y una primera incursión en
RL basado en una muestra. Le animamos a que lo compruebe.
Queríamos probar el algoritmo RR aproximado en la forma más simple posible
que naturalmente nos llevó al MNIST, el conjunto de datos ML canónico! Usamos
la versión aproximada para entrenar una red neuronal con dos 128 unidades ocultas
capas, y sorprendentemente fuimos capaces de obtener un 98% de precisión. Esto claramente no es un
nuevo SoTA para la visión por ordenador, pero creemos que es un buen resultado que muestra la
la posible escalabilidad de nuestro algoritmo.
Curiosamente, parece que las crestas individuales corresponden al aprendizaje de diferentes
características. En la siguiente figura, mostramos el rendimiento de un clasificador entrenado
siguiendo cada cresta individualmente.
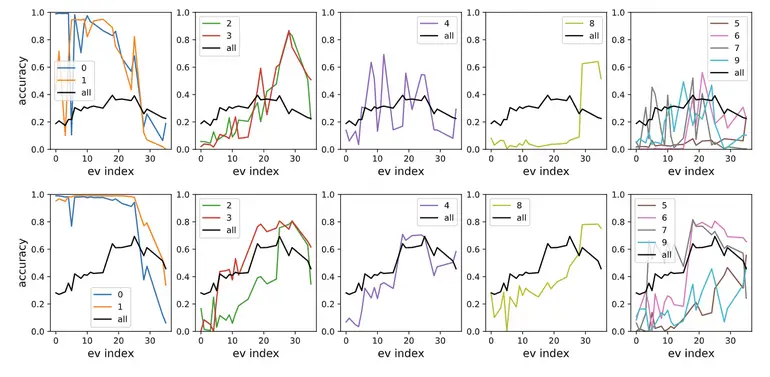
Como vemos, las primeras crestas corresponden al aprendizaje 0 y 1, mientras que las últimas
se aprende a clasificar el dígito 8.
Esto proporciona más pruebas de que el Hessian contiene una estructura que puede
se relacionan con la información causal sobre el problema. A continuación desarrollamos esto
mirando a la generalización de la distribución.
Probamos el RR en el conjunto de datos del MNIST de color, de [2]. El MNIST de color fue
diseñado específicamente para probar la causalidad, ya que cada imagen está coloreada en rojo o
verde de una manera que se correlaciona fuertemente (pero espuria) con la etiqueta de la clase.
Por construcción, la etiqueta está más fuertemente correlacionada con el color que con
el dígito. Cualquier algoritmo que minimice puramente el error de entrenamiento tenderá a explotar
el color.
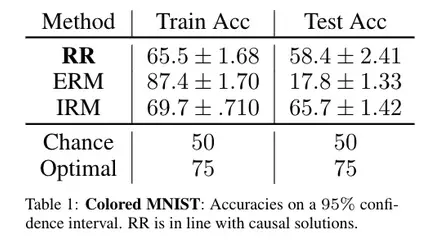
En la siguiente figura, vemos que ERM (optimizando ávidamente la pérdida en el entrenamiento
tiempo) se sobrepone masivamente al problema, y lo hace mal en el momento de la prueba. Por
En contraste, el RR alcanza un respetable 58%, no muy lejos del 66% alcanzado por
el enfoque causal de última generación.
Por último, consideramos el problema de la coordinación de disparo cero. En este escenario, nosotros
desean coordinarse con un socio, pero no pueden ver su política en la formación.
En su lugar, podemos acordar una estrategia de formación, por ejemplo, qué cresta a
seguir.
Utilizamos una versión adaptada del juego de palanca de [3]que se muestra a continuación:
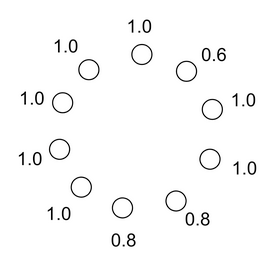
Recordemos que las simetrías conducen a valores propios repetidos. Esto significa que el
las palancas que comparten un pago con otros tendrán el mismo valor propio.
Además, el orden de las crestas correspondientes a los valores propios repetidos
es inconsistente a través de las diferentes carreras. Por lo tanto, sólo podemos coordinarnos de forma fiable en
direcciones únicas. Corrimos RR varias veces, y mostramos el resultado de tres
…corre independiente abajo.
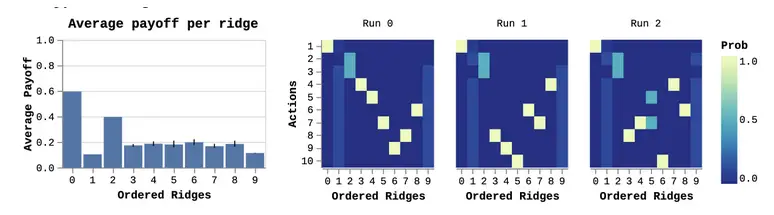
A la derecha, vemos que la primera cresta es siempre la misma acción, que
corresponde a la solución óptima de tiro cero. Los dos siguientes son una apuesta 50-50 a
las dos crestas de 0.8. Las crestas restantes son en gran parte un desorden mezclado,
que corresponden a las palancas con simetrías.
Un gif dice mil palabras:

Papel:
- Ridge Rider: Encontrando diversas soluciones siguiendo los vectores propios del Hessian.
Jack Parker-Holder, Luke Metz, Cinjon Resnick, Hengyuan Hu, Adam Lerer, Alistair Letcher, Alex Peysakhovich, Aldo Pacchiano, Jakob Foerster. NeurIPS 2020.
Enlace de papel
Código:
Referencias:
- [1] Robert Geirhos, Jörn-Henrik Jacobsen, Claudio Michaelis, Richard Zemel, Wieland Brendel, Matthias Bethge, Felix A. Wichmann (2020) Aprendizaje rápido en redes neuronales profundas.
- [2] Martin Arjovsky, Léon Bottou, Ishaan Gulrajani, David López-Paz (2019) Minimización del riesgo invariable. Pre-impresión de Arxiv.
- [3] Hengyuan Hu, Adam Lerer, Alex Peysakhovich y Jakob Foerster. «Other-Play» para la coordinación de tiro cero. Conferencia Internacional sobre Aprendizaje por Máquina (ICML). 2020

