Proponemos una métrica que mide la capacidad de un modelo para aumentar potencialmente la toma de decisiones médicas al reducir la incertidumbre en escenarios clínicos específicos. En la práctica, imaginamos que esta métrica se utilice durante las primeras fases del desarrollo del modelo (es decir, antes de calcular el beneficio neto) para modelos multiclase en entornos de atención dinámica como la atención crítica, que se están volviendo cada vez más comunes en la atención médica.19,20,21,22,23.
Para presentar nuestra métrica matemáticamente, primero sostenemos que la reducción de la incertidumbre en la toma de decisiones médicas podría reflejar las consideraciones de un proceso de decisión de Markov parcialmente observable (POMDP). En un marco POMDP, el médico busca determinar el diagnóstico «correcto» (en su estado de creencia) y el tratamiento «óptimo» mediante la predicción de resultados dada una acción particular tomada. Como tal, hay dos distribuciones de probabilidad clave involucradas: una en la fase de diagnóstico donde el médico busca aclarar la distribución de posibles diagnósticos, y una segunda en la fase de tratamiento donde el médico busca aclarar la distribución de estados futuros dadas acciones (es decir, , tratamientos) elegidos. El aprendizaje automático procesable debería reducir la incertidumbre de estas distribuciones.
El grado de reducción de la incertidumbre en estas distribuciones clave se puede cuantificar sobre la base de la entropía. La entropía es un concepto medible de la teoría de la información que cuantifica el nivel de incertidumbre de los posibles resultados de una variable aleatoria.24. Proponemos que los médicos pueden valorar la reducción de la entropía y, por lo tanto, nuestra métrica de accionabilidad se basa en el principio de que la accionabilidad aumenta con la capacidad de ML para disminuir progresivamente la entropía de las distribuciones de probabilidad centrales para la toma de decisiones médicas (Fig. 1).
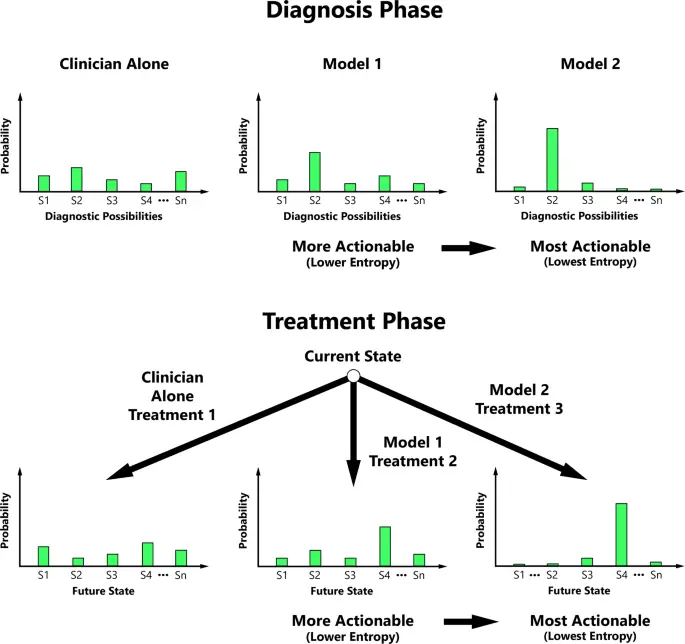
La accionabilidad generalmente aumenta con la disminución de la entropía de la distribución de probabilidad de posibilidad de diagnóstico y/o la distribución de probabilidad de estado futuro condicional durante las fases clave de la toma de decisiones médicas. S1 Estado 1, S2 Estado 2, S3 Estado 3, S4 Estado 4, Sn el N-ésimo Estado.
Volviendo al modelo multiclase que predice el diagnóstico en un paciente crítico con fiebre (entre una lista de posibles diagnósticos como infección, malignidad, insuficiencia cardíaca, fiebre por medicamentos, etc.), un investigador de ML podría usar la siguiente ecuación. La ecuación tiene fines ilustrativos, reconociendo que se necesitan datos adicionales para determinar los diagnósticos razonables en la lista de diagnósticos diferenciales y sus probabilidades de referencia. Este modelo de «médico solo» podría obtenerse pidiendo a una muestra de médicos que evalúen escenarios en tiempo real o retrospectivamente para determinar posibilidades de diagnóstico razonables y sus probabilidades en función de los datos clínicos disponibles.
Para cada muestra en un conjunto de datos de prueba, se calcula la entropía de la salida del modelo candidato (es decir, la distribución de probabilidad de los diagnósticos predichos) y se compara con la entropía de la salida del modelo de referencia, que por defecto es el modelo solo del médico. pero también pueden ser otros modelos ML. Las diferencias se promedian entre todas las muestras para determinar la reducción neta de la entropía (ML—referencia) como se ilustra a continuación utilizando la notación común a los POMDP:
(1) Modelo de médico solo:
$$H^s_c = – mathop {sum}limits_{s_t in S} {p_c(s_t|o_t)log;p_c(s_t|o_t)}$$
(2) Con ML Modelo 1:
$$H^s_{m1} = – mathop {sum}limits_{s_t in S} {p_{m1}(s_t|o_t)log;p_{m1}(s_t|o_t)}$$
(3) Con ML Modelo 2:
$$H^s_{m2} = – mathop {sum}limits_{s_t in S} {p_{m2}(s_t|o_t)log;p_{m2}(s_t|o_t)}$$
Por lo cual, (s_t en S) es el estado subyacente del paciente (p. ej., infección) en el tiempo t dentro de un dominio S correspondiente a un conjunto de todos los estados posibles razonables (p. ej., diferentes causas de fiebre, incluidas, entre otras, las infecciones) y (o_t en O)son las observaciones clínicas (p. ej., diagnósticos previos e historial médico, examen físico actual, datos de laboratorio, datos de imágenes, etc.) en el momento t dentro de un dominio O correspondiente al conjunto de todas las observaciones posibles.
Por lo tanto, la capacidad de acción del modelo de ML candidato en la fase de diagnóstico (es decir, estado actual) (Δs) se puede cuantificar como: (Delta ^{{{s}}} = {{{H}}}^{{{s}}}_{{{0}}} – {{{H}}}^{{{s} }}_{{{metro}}})donde ({{{H}}}_{{{0}}}^{{{s}}}) es la entropía correspondiente a la distribución de referencia (típicamente el modelo clínico solo, correspondiente a ({{{H}}}^{{{s}}}_{{{c}}})).
Básicamente, el modelo aprende la distribución condicional de los diversos diagnósticos subyacentes posibles dadas las observaciones (consulte el ejemplo de cálculo en la Fig. 1 complementaria). El alcance de la capacidad de acción de un modelo es la reducción medible de la entropía cuando se usa el modelo ML en comparación con el modelo de referencia.
Continuando con el ejemplo clínico anterior, el médico debe elegir una acción a realizar, por ejemplo, qué régimen de antibióticos prescribir entre una selección de muchos regímenes de antibióticos razonables. Cada par estado-acción se asigna probabilísticamente a diferentes estados futuros potenciales, que por lo tanto tienen una entropía de distribución. Reconociendo que se necesitan datos adicionales para definir las probabilidades de transición relevantes (p^ ast (s_{t + 1}|s_{t,}a_t)) (es decir, proporciones de beneficio:riesgo) para cada par estado-acción (que idealmente pueden ser estimados por médicos o datos derivados empíricamente de cohortes retrospectivas representativas), un investigador de ML podría realizar una evaluación de capacidad de acción de modelos multiclase candidatos. La evaluación de la capacidad de acción depende de la comparación de las entropías de las distribuciones de estado futuro con y sin ML y se calcula de manera similar a la fase de diagnóstico, donde se calculan las diferencias en la entropía de distribución (modelo de referencia – modelo ML candidato) para cada muestra en la prueba. conjunto de datos y luego se promedia. La siguiente ecuación, o una variación de la misma, podría usarse para determinar la capacidad de acción durante la fase de atención del tratamiento:
Distribución de probabilidad de estado futuro (P (st+1|st)
(4) Sin ML (p. ej., acción/política del médico solo):
$$p_c(s_{t + 1}|s_t) = mathop {sum}limits_{a_t in A} {p^ ast (s_{t + 1}|s_{t,}a_t)pi _c(a_t|s_t)}$$
(5) Con ML (p. ej., la acción/política recomendada por el modelo entrenado):
$$p_m(s_{t + 1}|s_t) = mathop {sum}limits_{a_t in A} {p^ ast (s_{t + 1}|s_{t,}a_t)pi _m(a_t|s_t)}$$
Por lo cual, St+1 es el estado futuro deseado (p. ej., resolución de la infección), St es el estado actual (p. ej., fiebre) en el momento t, (a_t en A) es la acción tomada en el momento t dentro de un dominio A correspondiente a un conjunto de posibles acciones razonables (es decir, diferentes regímenes de antibióticos), (pi _c(a_t|s_t)) es la política elegida por el médico en el momento t (p. ej., tratar con el régimen antibiótico A) y (pi _m(a_t|s_t)) es la política recomendada por ML en el momento t (p. ej., tratar con el régimen antibiótico B).
Entropía (H) de la distribución de probabilidad del estado futuro
Cada distribución de probabilidad de estado futuro proviene de una distribución de posibles estados futuros con entropía asociada, que ilustramos como:
(6) Sin ML:
$$H^a_0 = – mathop {sum}limits_{s_{t + 1} in S} {p_0(s_{t + 1}|s_t)log;p_0(s_{t + 1}| mierda)}$$
(7) Con ML:
$$H^a_m = – mathop {sum}limits_{s_{t + 1} in S} {p_0(s_{t + 1}|s_t)log;p_m(s_{t + 1}| mierda)}$$
Por lo tanto, la accionabilidad del modelo ML candidato en la fase de acción (es decir, estado futuro) (Δa) se puede cuantificar como (Delta ^{{{a}}} = {{{H}}}^{{{a}}}_0 – {{{H}}}^{{a}}_{{{m}} })donde ({{{H}}}_0^{{{a}}}) es la entropía correspondiente a la distribución de referencia (típicamente el modelo clínico solo).
Básicamente, el modelo aprende la distribución condicional de los estados futuros dadas las acciones realizadas en el estado actual, y la capacidad de acción es la reducción medible de la entropía cuando se utiliza el modelo ML frente al modelo de referencia (normalmente solo el médico).
