La optimización de funciones es un campo de estudio que busca una entrada a una función que da como resultado la salida máxima o mínima de la función.
Existe una gran cantidad de algoritmos de optimización y es importante estudiar y desarrollar intuiciones para algoritmos de optimización en funciones de prueba simples y fáciles de visualizar.
Funciones bidimensionales tomar dos valores de entrada (xey) y generar una única evaluación de la entrada. Se encuentran entre los tipos más simples de funciones de prueba para usar al estudiar la optimización de funciones. El beneficio de las funciones bidimensionales es que se pueden visualizar como un gráfico de contorno o gráfico de superficie que muestra la topografía del dominio del problema con los óptimos y las muestras del dominio marcadas con puntos.
En este tutorial, descubrirá funciones bidimensionales estándar que puede utilizar al estudiar la optimización de funciones.
Empecemos.

Funciones de prueba bidimensionales (2D) para la optimización de funciones
Foto de DomWphoto, algunos derechos reservados.
Descripción general del tutorial
Una función bidimensional es una función que toma dos variables de entrada y calcula el valor objetivo.
Podemos pensar en las dos variables de entrada como dos ejes en un gráfico, xey. Cada entrada a la función es un solo punto en el gráfico y el resultado de la función se puede tomar como la altura en el gráfico.
Esto permite conceptualizar la función como una superficie y podemos caracterizar la función en función de la estructura de la superficie. Por ejemplo, colinas para puntos de entrada que dan como resultado grandes resultados relativos de la función objetivo y valles para puntos de entrada que dan como resultado pequeños resultados relativos de la función objetivo.
Una superficie puede tener una característica principal u óptimos globales, o puede tener muchos con muchos lugares para que una optimización se atasque. La superficie puede ser lisa, ruidosa, convexa y todo tipo de otras propiedades que pueden interesarnos al probar los algoritmos de optimización.
Hay muchos tipos diferentes de funciones de prueba bidimensionales simples que podemos utilizar.
Sin embargo, existen funciones de prueba estándar que se utilizan comúnmente en el campo de la optimización de funciones. También hay propiedades específicas de las funciones de prueba que es posible que deseemos seleccionar al probar diferentes algoritmos.
Exploraremos una pequeña cantidad de funciones de prueba bidimensionales simples en este tutorial y las organizaremos por sus propiedades con dos grupos diferentes; son:
- Funciones unimodales
- Función unimodal 1
- Función unimodal 2
- Función unimodal 3
- Funciones multimodales
- Función multimodal 1
- Función multimodal 2
- Función multimodal 3
Cada función se presentará utilizando código Python con una implementación de función de la función objetivo de destino y una muestra de la función que se muestra como un diagrama de superficie.
Todas las funciones se presentan como una función de minimización, p. Ej. encuentre la entrada que dé como resultado la salida mínima (valor más pequeño) de la función. Cualquier función maximizadora se puede convertir en una función de minimización agregando un signo negativo a toda la salida. De manera similar, cualquier función de minimización se puede hacer maximizando de la misma manera.
Yo no inventé estas funciones; se toman de la literatura. Consulte la sección de lectura adicional para obtener referencias.
Luego puede elegir y copiar y pegar el código una o más funciones para usar en su propio proyecto para estudiar o comparar el comportamiento de los algoritmos de optimización.
Funciones unimodales
Unimodal significa que la función tiene un único óptimo global.
Una función unimodal puede ser convexa o no. Una función convexa es una función en la que se puede trazar una línea entre dos puntos cualesquiera en el dominio y la línea permanece en el dominio. Para una función bidimensional mostrada como un contorno o un gráfico de superficie, esto significa que la función tiene forma de cuenco y la línea entre dos permanece arriba o en el cuenco.
Veamos algunos ejemplos de funciones unimodales.
Función unimodal 1
El rango está limitado a -5.0 y 5.0 y un óptimo global en [0.0, 0.0].
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 |
# función de prueba unimodal desde numpy importar arange desde numpy importar rejilla desde matplotlib importar pyplot desde mpl_toolkits.mplot3d importar Ejes3D # función objetiva def objetivo(X, y): regreso X**2.0 + y **2.0 # definir rango para entrada r_min, r_max = –5,0, 5,0 # rango de entrada de muestra uniformemente en incrementos de 0.1 xaxis = arange(r_min, r_max, 0,1) yaxis = arange(r_min, r_max, 0,1) # crea una malla a partir del eje X, y = rejilla(xaxis, yaxis) # calcular objetivos resultados = objetivo(X, y) # crea un gráfico de superficie con el esquema de color jet figura = pyplot.figura() eje = figura.gca(proyección=‘3d’) eje.plot_surface(X, y, resultados, cmap=‘chorro’) # mostrar la trama pyplot.show() |
La ejecución del ejemplo crea un gráfico de superficie de la función.
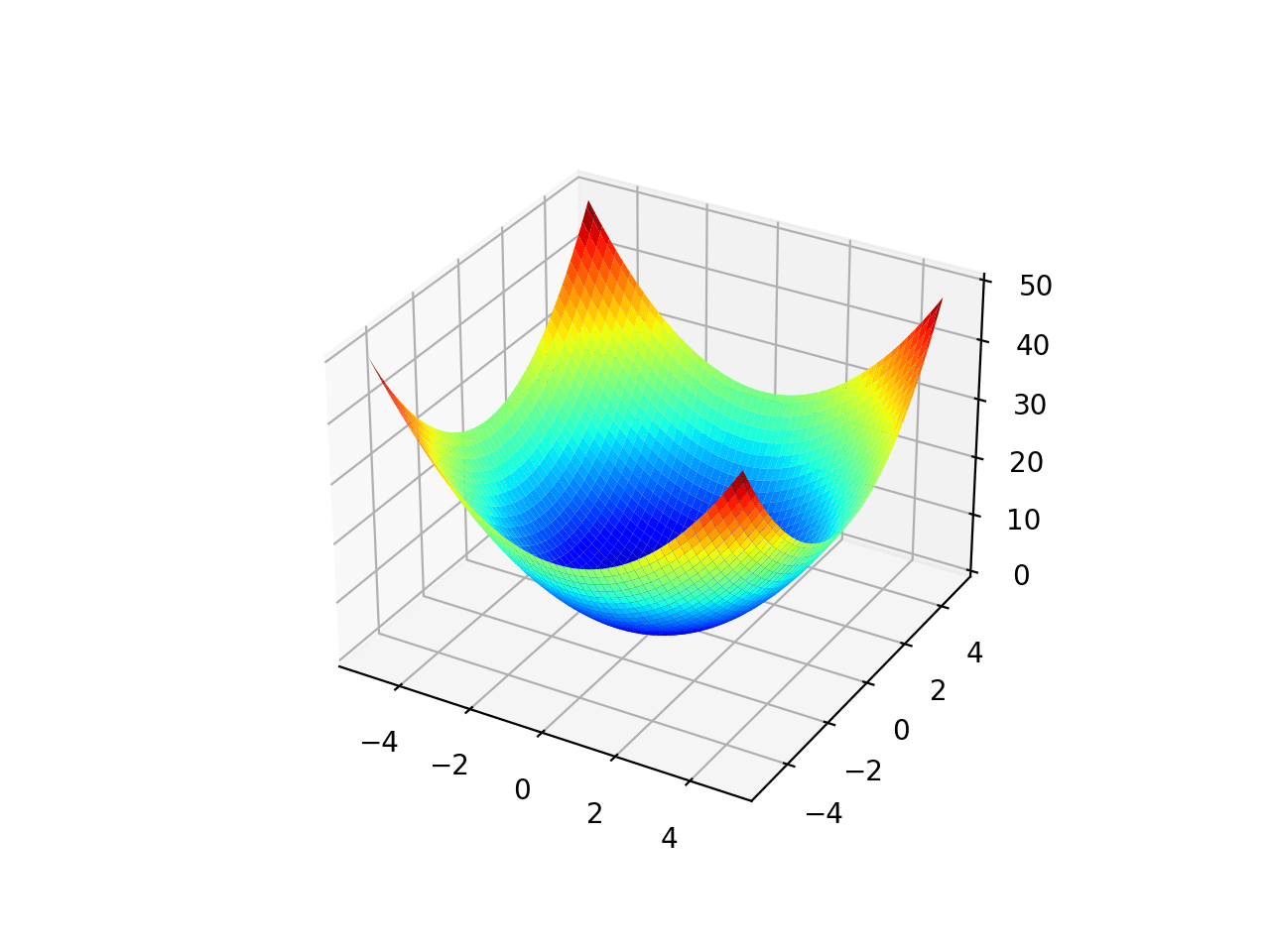
Gráfico de superficie de la función de optimización unimodal 1
Función unimodal 2
El rango está limitado a -10.0 y 10.0 y un óptimo global en [0.0, 0.0].
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 |
# función de prueba unimodal desde numpy importar arange desde numpy importar rejilla desde matplotlib importar pyplot desde mpl_toolkits.mplot3d importar Ejes3D # función objetiva def objetivo(X, y): regreso 0,26 * (X**2 + y **2) – 0,48 * X * y # definir rango para entrada r_min, r_max = –10.0, 10.0 # rango de entrada de muestra uniformemente en incrementos de 0.1 xaxis = arange(r_min, r_max, 0,1) yaxis = arange(r_min, r_max, 0,1) # crea una malla a partir del eje X, y = rejilla(xaxis, yaxis) # calcular objetivos resultados = objetivo(X, y) # crea un gráfico de superficie con el esquema de color jet figura = pyplot.figura() eje = figura.gca(proyección=‘3d’) eje.plot_surface(X, y, resultados, cmap=‘chorro’) # mostrar la trama pyplot.show() |
La ejecución del ejemplo crea un gráfico de superficie de la función.
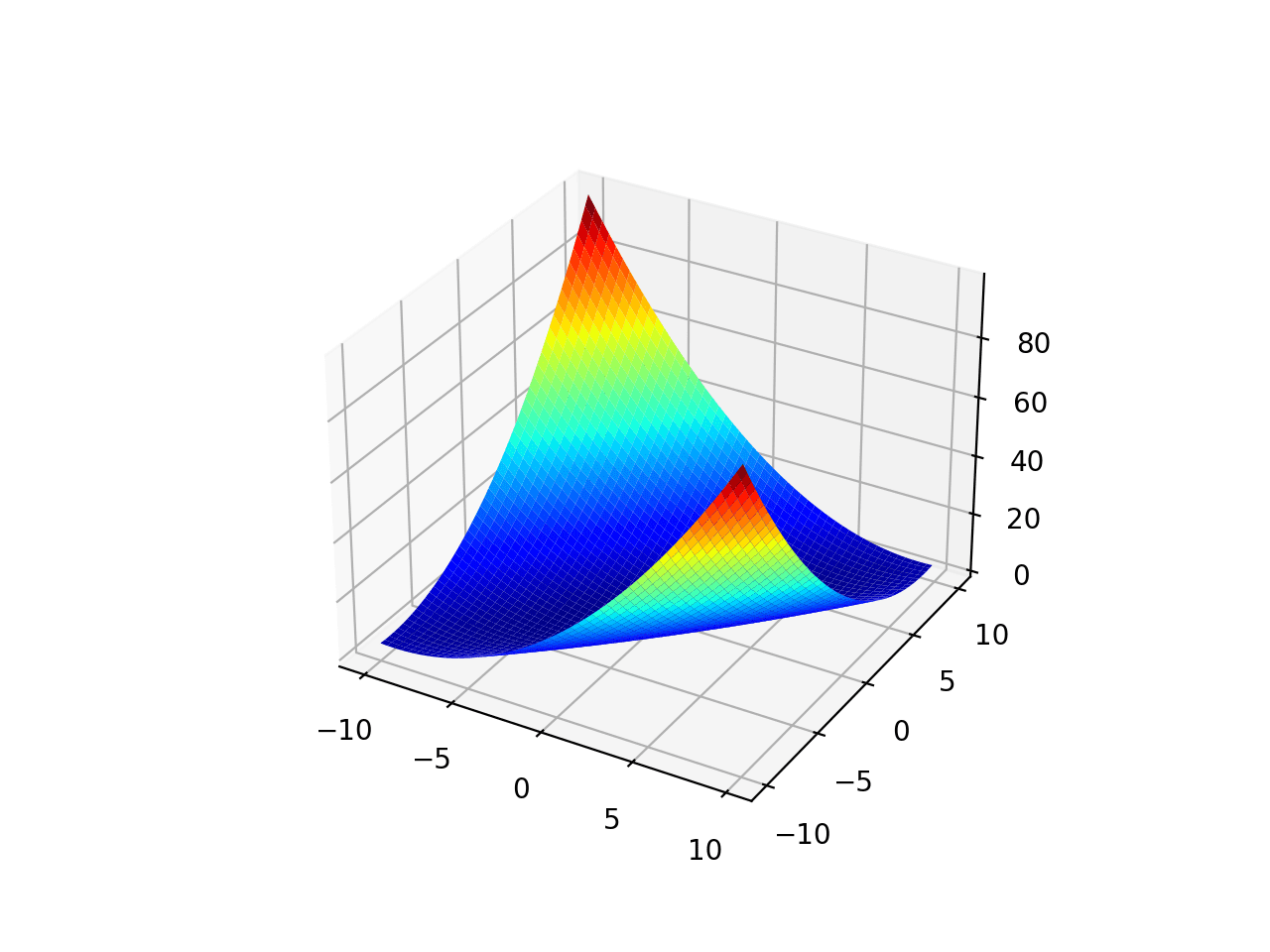
Gráfico de superficie de la función de optimización unimodal 2
Función unimodal 3
El rango está limitado a -10.0 y 10.0 y un óptimo global en [0.0, 0.0]. Esta función se conoce como función de Easom.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 |
# función de prueba unimodal desde numpy importar porque desde numpy importar Exp desde numpy importar Pi desde numpy importar arange desde numpy importar rejilla desde matplotlib importar pyplot desde mpl_toolkits.mplot3d importar Ejes3D # función objetiva def objetivo(X, y): regreso –porque(X) * porque(y) * Exp(–((X – Pi)**2 + (y – Pi)**2)) # definir rango para entrada r_min, r_max = –10, 10 # rango de entrada de muestra uniformemente en incrementos de 0.01 xaxis = arange(r_min, r_max, 0,01) yaxis = arange(r_min, r_max, 0,01) # crea una malla a partir del eje X, y = rejilla(xaxis, yaxis) # calcular objetivos resultados = objetivo(X, y) # crea un gráfico de superficie con el esquema de color jet figura = pyplot.figura() eje = figura.gca(proyección=‘3d’) eje.plot_surface(X, y, resultados, cmap=‘chorro’) # mostrar la trama pyplot.show() |
La ejecución del ejemplo crea un gráfico de superficie de la función.
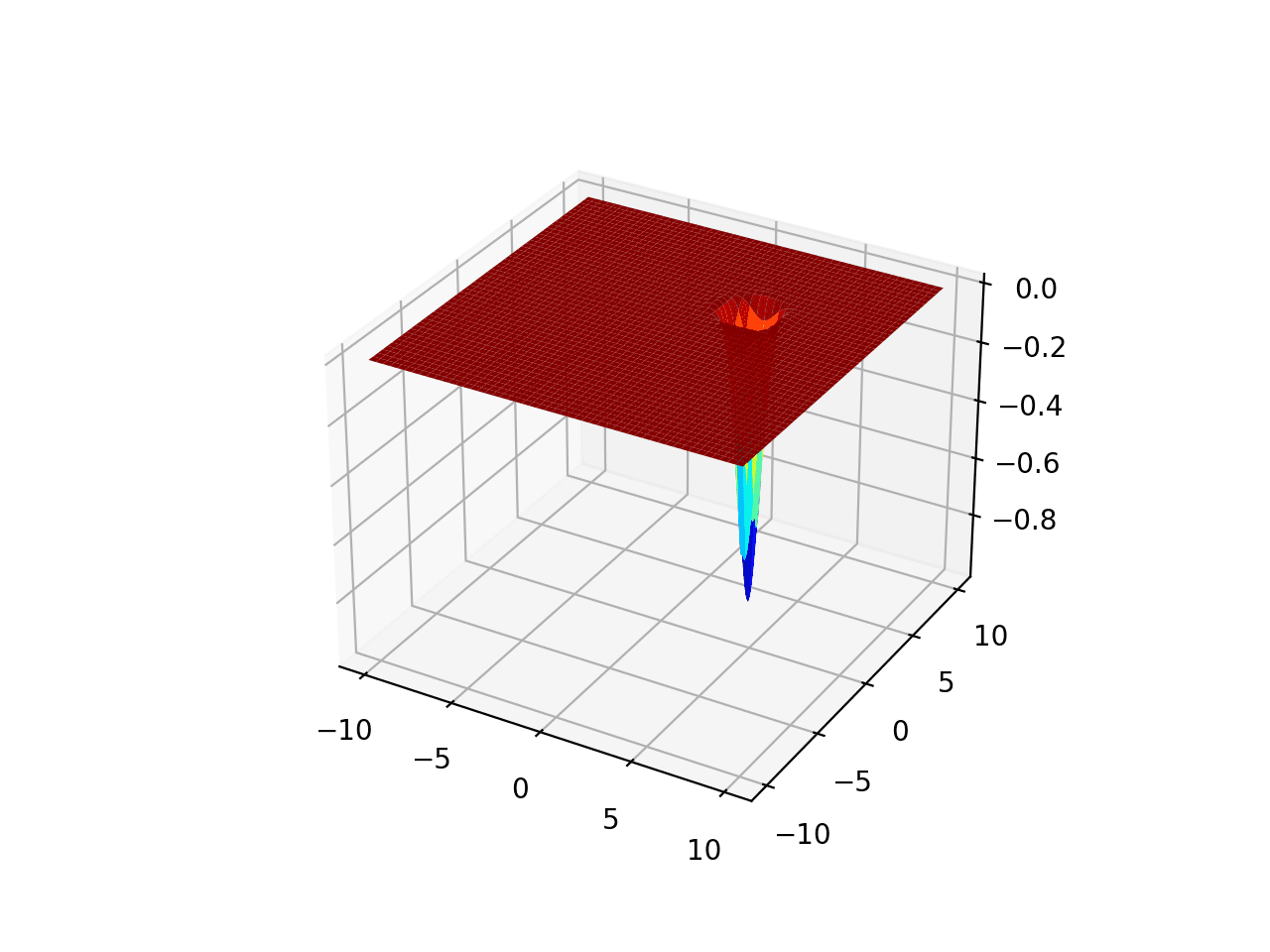
Gráfico de superficie de la función de optimización unimodal 3
Funciones multimodales
Una función multimodal significa una función con más de una «modo”U optima (por ejemplo, valle).
Las funciones multimodales no son convexas.
Puede haber un óptimo global y uno o más óptimos locales o engañosos. Alternativamente, puede haber múltiples óptimos globales, es decir, múltiples entradas diferentes que dan como resultado la misma salida mínima de la función.
Veamos algunos ejemplos de funciones multimodales.
Función multimodal 1
El rango está limitado a -5.0 y 5.0 y un óptimo global en [0.0, 0.0]. Esta función se conoce como función de Ackley.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
# función de prueba multimodal desde numpy importar arange desde numpy importar Exp desde numpy importar sqrt desde numpy importar porque desde numpy importar mi desde numpy importar Pi desde numpy importar rejilla desde matplotlib importar pyplot desde mpl_toolkits.mplot3d importar Ejes3D # función objetiva def objetivo(X, y): regreso –20,0 * Exp(–0,2 * sqrt(0,5 * (X**2 + y **2))) – Exp(0,5 * (porque(2 * Pi * X) + porque(2 * Pi * y))) + mi + 20 # definir rango para entrada r_min, r_max = –5,0, 5,0 # rango de entrada de muestra uniformemente en incrementos de 0.1 xaxis = arange(r_min, r_max, 0,1) yaxis = arange(r_min, r_max, 0,1) # crea una malla a partir del eje X, y = rejilla(xaxis, yaxis) # calcular objetivos resultados = objetivo(X, y) # crea un gráfico de superficie con el esquema de color jet figura = pyplot.figura() eje = figura.gca(proyección=‘3d’) eje.plot_surface(X, y, resultados, cmap=‘chorro’) # mostrar la trama pyplot.show() |
La ejecución del ejemplo crea un gráfico de superficie de la función.
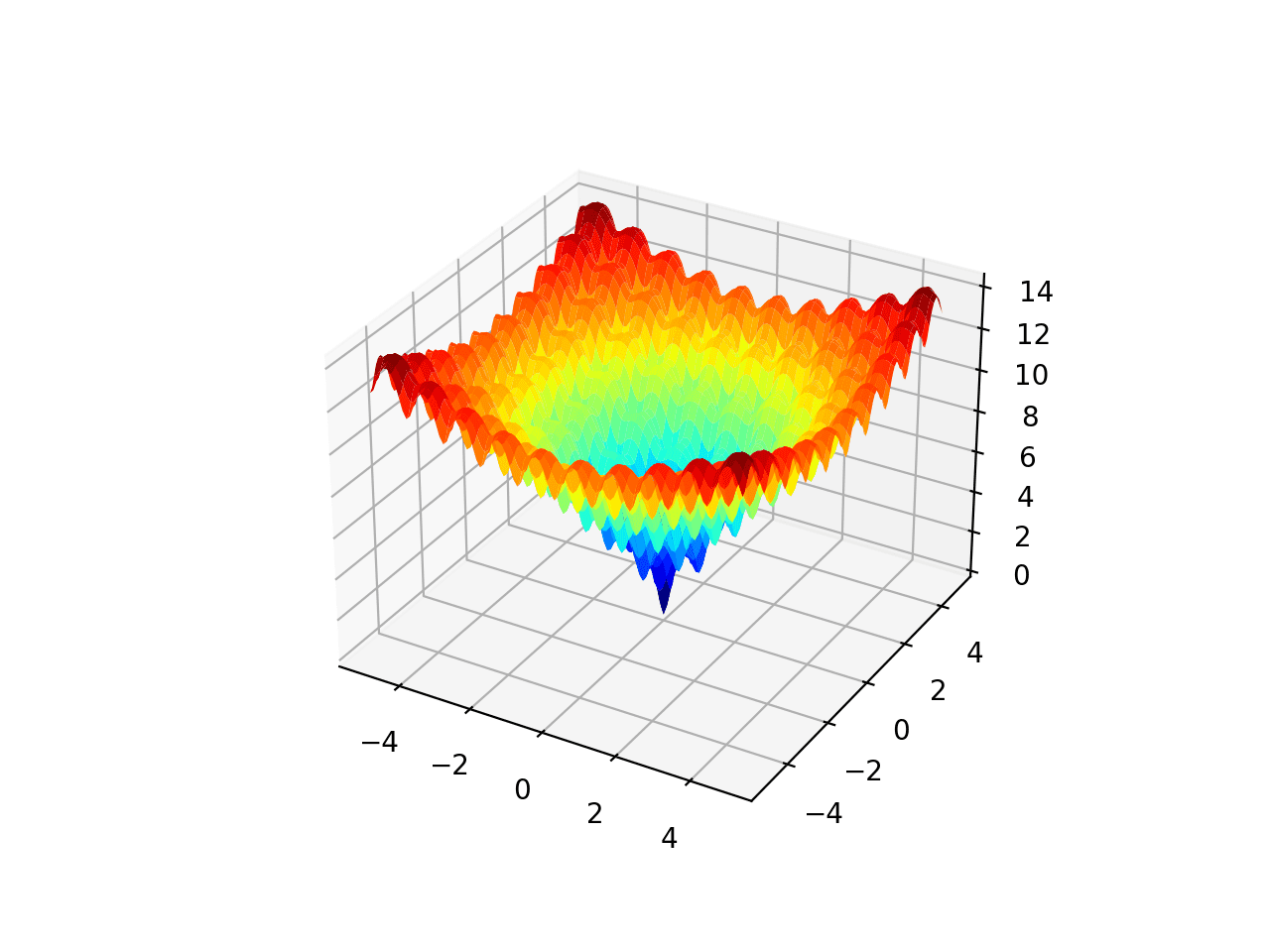
Gráfico de superficie de la función de optimización multimodal 1
Función multimodal 2
El rango está limitado a -5.0 y 5.0 y la función como cuatro óptimos globales en [3.0, 2.0], [-2.805118, 3.131312], [-3.779310, -3.283186], [3.584428, -1.848126]. Esta función se conoce como función de Himmelblau.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 |
# función de prueba multimodal desde numpy importar arange desde numpy importar rejilla desde matplotlib importar pyplot desde mpl_toolkits.mplot3d importar Ejes3D # función objetiva def objetivo(X, y): regreso (X**2 + y – 11)**2 + (X + y **2 –7)**2 # definir rango para entrada r_min, r_max = –5,0, 5,0 # rango de entrada de muestra uniformemente en incrementos de 0.1 xaxis = arange(r_min, r_max, 0,1) yaxis = arange(r_min, r_max, 0,1) # crea una malla a partir del eje X, y = rejilla(xaxis, yaxis) # calcular objetivos resultados = objetivo(X, y) # crea un gráfico de superficie con el esquema de color jet figura = pyplot.figura() eje = figura.gca(proyección=‘3d’) eje.plot_surface(X, y, resultados, cmap=‘chorro’) # mostrar la trama pyplot.show() |
La ejecución del ejemplo crea un gráfico de superficie de la función.
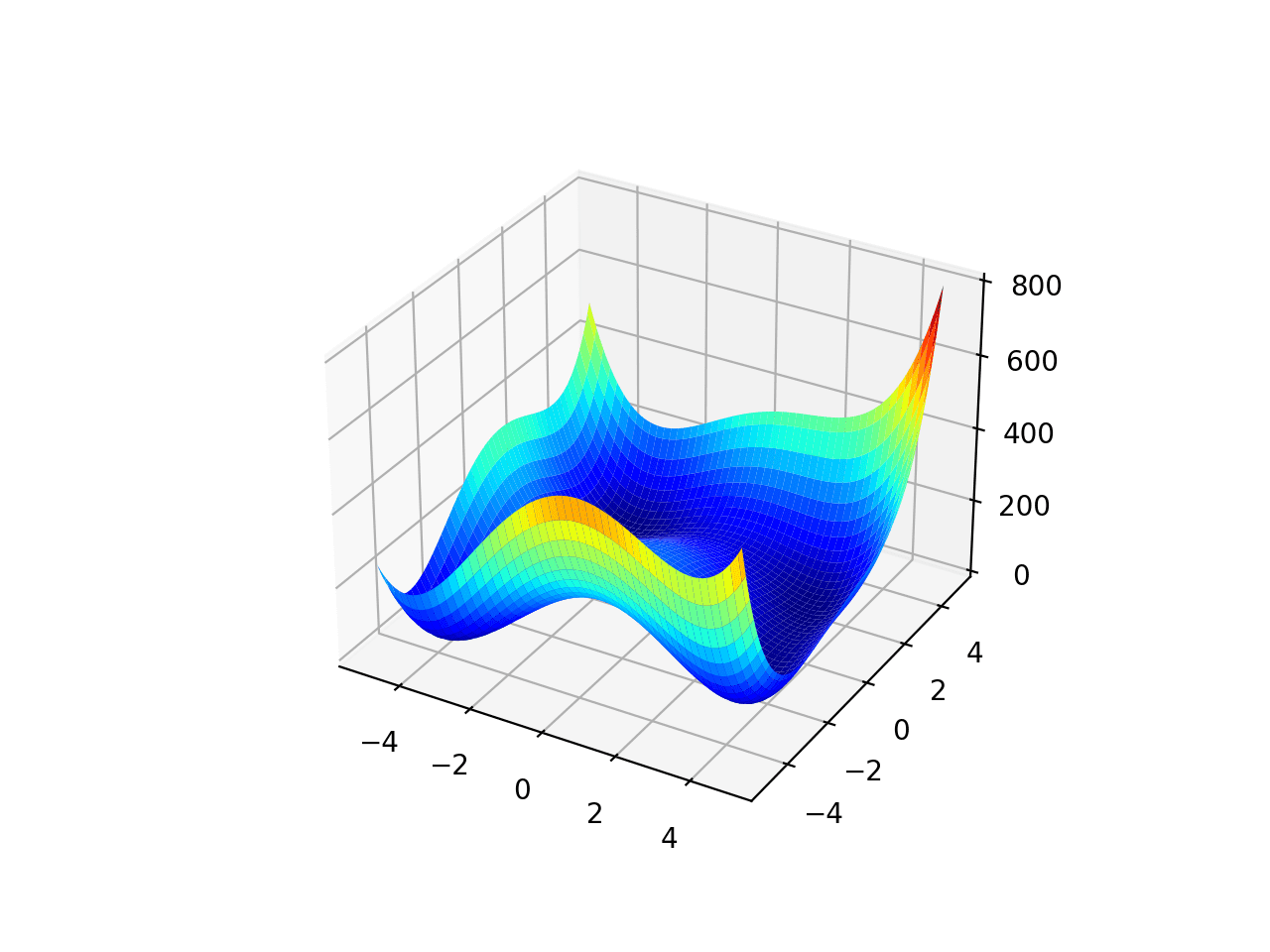
Gráfico de superficie de la función de optimización multimodal 2
Función multimodal 3
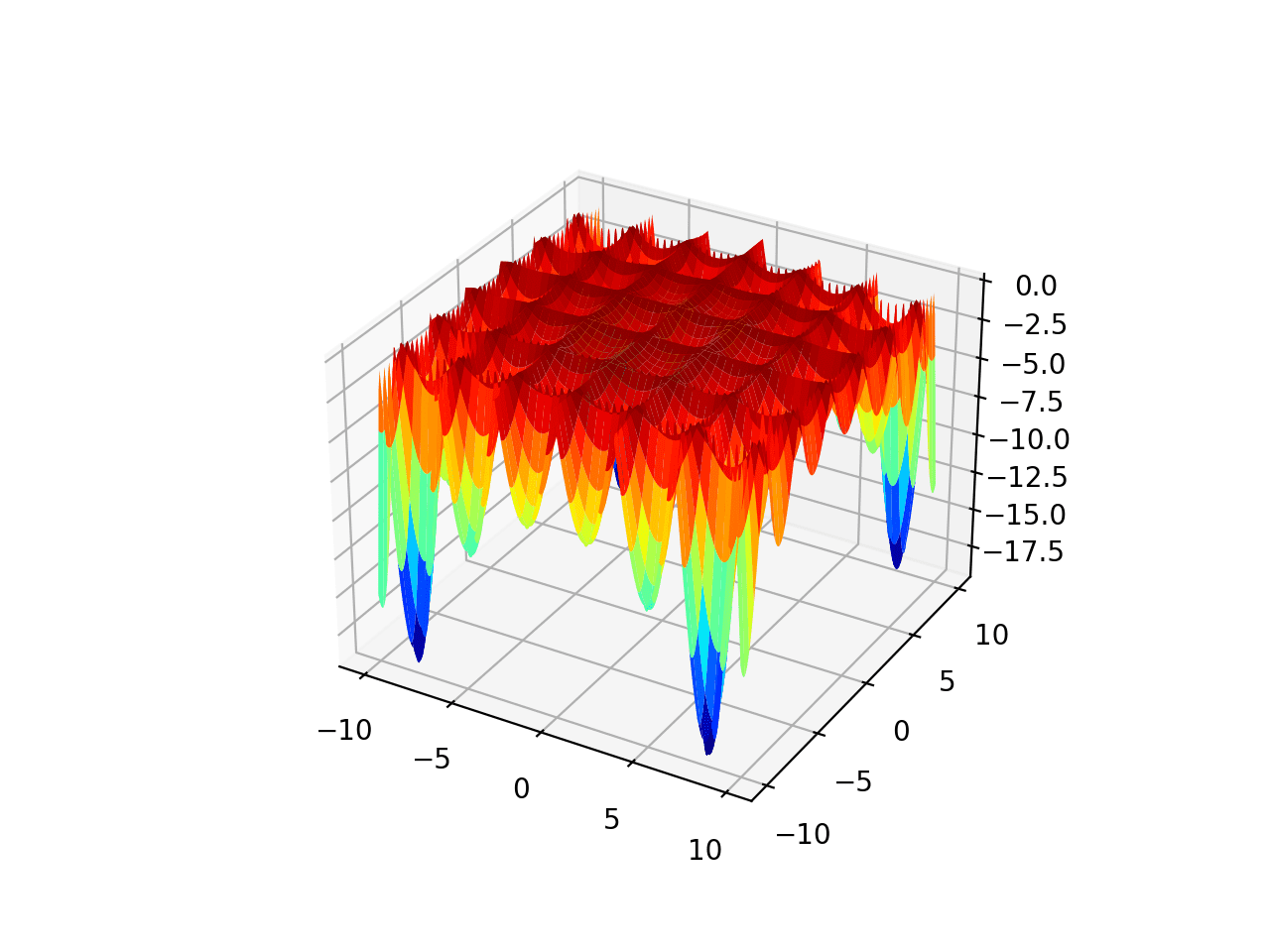
El rango está limitado a -10.0 y 10.0 y la función como cuatro óptimos globales en [8.05502, 9.66459], [-8.05502, 9.66459], [8.05502, -9.66459], [-8.05502, -9.66459]. Esta función se conoce como función de tabla de Holder.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
# función de prueba multimodal desde numpy importar arange desde numpy importar Exp desde numpy importar sqrt desde numpy importar porque desde numpy importar pecado desde numpy importar mi desde numpy importar Pi desde numpy importar absoluto desde numpy importar rejilla desde matplotlib importar pyplot desde mpl_toolkits.mplot3d importar Ejes3D # función objetiva def objetivo(X, y): regreso –absoluto(pecado(X) * porque(y) * Exp(absoluto(1 – (sqrt(X**2 + y **2)/Pi)))) # definir rango para entrada r_min, r_max = –10.0, 10.0 # rango de entrada de muestra uniformemente en incrementos de 0.1 xaxis = arange(r_min, r_max, 0,1) yaxis = arange(r_min, r_max, 0,1) # crea una malla a partir del eje X, y = rejilla(xaxis, yaxis) # calcular objetivos resultados = objetivo(X, y) # crea un gráfico de superficie con el esquema de color jet figura = pyplot.figura() eje = figura.gca(proyección=‘3d’) eje.plot_surface(X, y, resultados, cmap=‘chorro’) # mostrar la trama pyplot.show() |
La ejecución del ejemplo crea un gráfico de superficie de la función.

Gráfico de superficie de la función de optimización multimodal 3
Otras lecturas
Esta sección proporciona más recursos sobre el tema si desea profundizar.
Artículos
Resumen
En este tutorial, descubrió funciones bidimensionales estándar que puede usar al estudiar la optimización de funciones.
¿Está utilizando alguna de las funciones anteriores?
Déjame saber cuál en los comentarios a continuación.
¿Tiene usted alguna pregunta?
Haga sus preguntas en los comentarios a continuación y haré todo lo posible para responder.
