Estrategias de evolución es un algoritmo de optimización global estocástico.
Es un algoritmo evolutivo relacionado con otros, como el algoritmo genético, aunque está diseñado específicamente para la optimización continua de funciones.
En este tutorial, descubrirá cómo implementar el algoritmo de optimización de estrategias de evolución.
Después de completar este tutorial, sabrá:
- Evolution Strategies es un algoritmo estocástico de optimización global inspirado en la teoría biológica de la evolución por selección natural.
- Existe una terminología estándar para las estrategias de evolución y dos versiones comunes del algoritmo denominadas (mu, lambda) -ES y (mu + lambda) -ES.
- Cómo implementar y aplicar el algoritmo Evolution Strategies a funciones objetivas continuas.
Empecemos.

Estrategias de evolución desde cero en Python
Foto de Alexis A. Bermúdez, algunos derechos reservados.
Descripción general del tutorial
Este tutorial se divide en tres partes; son:
- Estrategias de evolución
- Desarrollar un (mu, lambda) -ES
- Desarrollar un (mu + lambda) -ES
Estrategias de evolución
Las estrategias de evolución, a veces denominadas estrategia de evolución (singular) o ES, es un algoritmo de optimización global estocástico.
La técnica fue desarrollada en la década de 1960 para ser implementada manualmente por ingenieros para diseños de arrastre mínimo en un túnel de viento.
La familia de algoritmos conocida como Evolution Strategies (ES) fue desarrollada por Ingo Rechenberg y Hans-Paul Schwefel en la Universidad Técnica de Berlín a mediados de la década de 1960.
– Página 31, Fundamentos de metaheurística, 2011.
Evolution Strategies es un tipo de algoritmo evolutivo y está inspirado en la teoría biológica de la evolución por medio de la selección natural. A diferencia de otros algoritmos evolutivos, no utiliza ninguna forma de cruce; en cambio, la modificación de las soluciones candidatas se limita a los operadores de mutación. De esta manera, las Estrategias de Evolución se pueden considerar como un tipo de escalada estocástica paralela.
El algoritmo involucra una población de soluciones candidatas que inicialmente se generan aleatoriamente. Cada iteración del algoritmo implica primero evaluar la población de soluciones y luego eliminar todas menos un subconjunto de las mejores soluciones, lo que se conoce como selección de truncamiento. Las soluciones restantes (los padres) se utilizan como base para generar una serie de nuevas soluciones candidatas (mutación) que reemplazan o compiten con los padres por una posición en la población para su consideración en la próxima iteración del algoritmo (generación).
Hay una serie de variaciones de este procedimiento y una terminología estándar para resumir el algoritmo. El tamaño de la población se conoce como lambda y el número de padres seleccionados en cada iteración se denomina mu.
El número de hijos creados a partir de cada padre se calcula como (lambda / mu) y los parámetros deben elegirse de modo que la división no tenga resto.
- mu: El número de padres seleccionados en cada iteración.
- lambda: Tamaño de la población.
- lambda / mu: Número de hijos generados por cada padre seleccionado.
Se utiliza una notación entre corchetes para describir la configuración del algoritmo, p. Ej. (mu, lambda) -ES. Por ejemplo, si mu = 5 y lambda = 20, entonces se resumiría como (5, 20) -ES. Una coma (,) que separa el mu y lambda parámetros indica que los hijos reemplazan a los padres directamente en cada iteración del algoritmo.
- (mu, lambda) -ES: Una versión de las estrategias de evolución donde los niños reemplazan a los padres.
Una separación más (+) de los parámetros mu y lambda indica que los niños y los padres juntos definirán la población para la siguiente iteración.
- (mu + lambda) -ES: Una versión de las estrategias de evolución donde los niños y los padres se suman a la población.
Un algoritmo de escalada estocástico se puede implementar como una estrategia de evolución y tendría la notación (1 + 1) -ES.
Este es el algoritmo ES símil o canónico y hay muchas extensiones y variantes descritas en la literatura.
Ahora que estamos familiarizados con Evolution Strategies, podemos explorar cómo implementar el algoritmo.
Desarrollar un (mu, lambda) -ES
En esta sección, desarrollaremos un (mu, lambda) -ES, es decir, una versión del algoritmo donde los niños reemplazan a los padres.
Primero, definamos un problema de optimización desafiante como la base para implementar el algoritmo.
La función Ackley es un ejemplo de una función objetivo multimodal que tiene un único óptimo global y múltiples óptimos locales en los que una búsqueda local puede atascarse.
Como tal, se requiere una técnica de optimización global. Es una función objetivo bidimensional que tiene un óptimo global en [0,0], que se evalúa como 0.0.
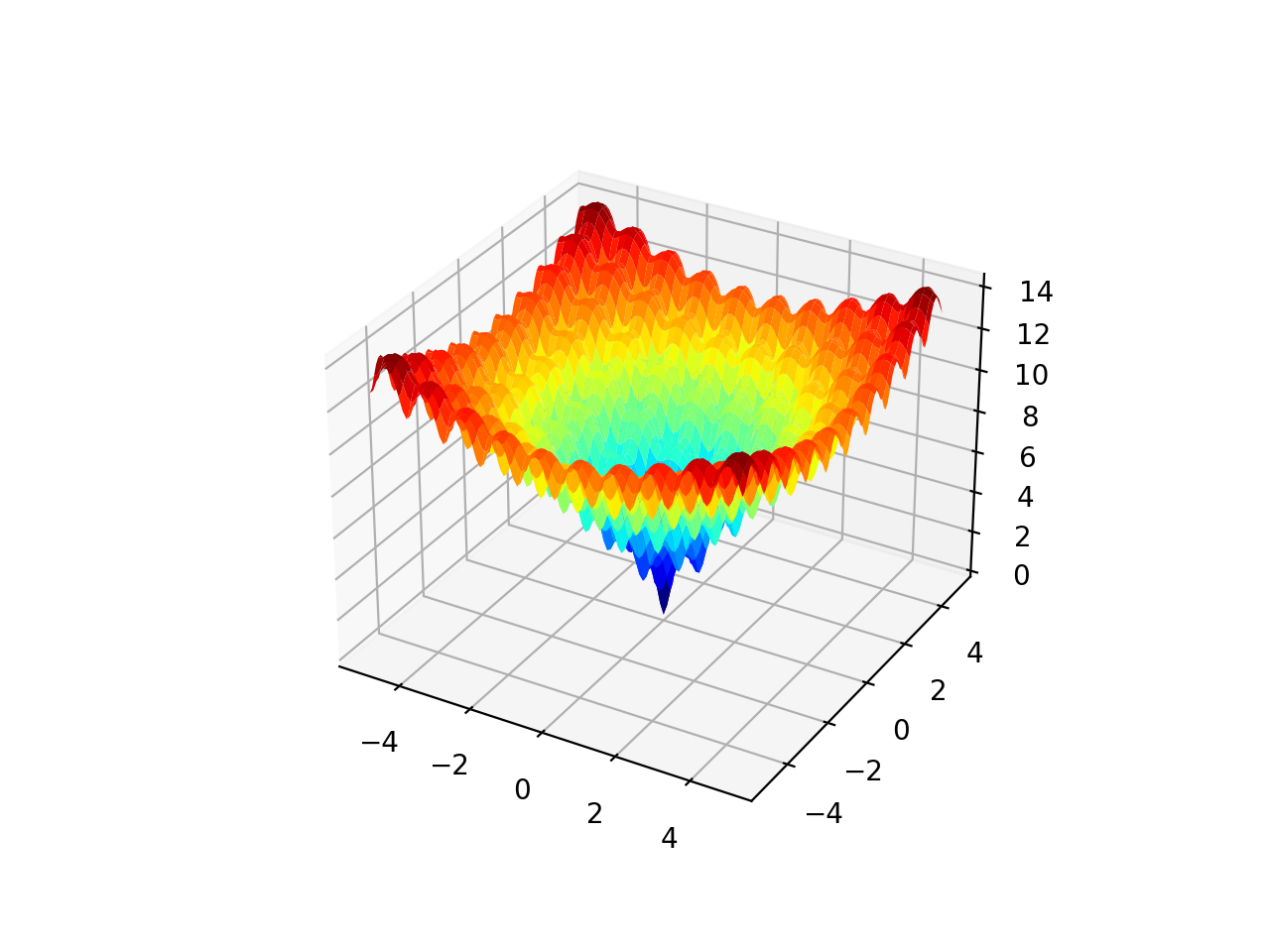
El siguiente ejemplo implementa el Ackley y crea un gráfico de superficie tridimensional que muestra los óptimos globales y múltiples óptimos locales.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
# función multimodal ackley desde numpy importar arange desde numpy importar Exp desde numpy importar sqrt desde numpy importar porque desde numpy importar mi desde numpy importar Pi desde numpy importar rejilla desde matplotlib importar pyplot desde mpl_toolkits.mplot3d importar Ejes3D # función objetiva def objetivo(X, y): regreso –20,0 * Exp(–0,2 * sqrt(0,5 * (X**2 + y **2))) – Exp(0,5 * (porque(2 * Pi * X) + porque(2 * Pi * y))) + mi + 20 # definir rango para entrada r_min, r_max = –5,0, 5,0 # rango de entrada de muestra uniformemente en incrementos de 0.1 xaxis = arange(r_min, r_max, 0,1) yaxis = arange(r_min, r_max, 0,1) # crea una malla desde el eje X, y = rejilla(xaxis, yaxis) # calcular objetivos resultados = objetivo(X, y) # crea un gráfico de superficie con el esquema de color jet figura = pyplot.figura() eje = figura.gca(proyección=‘3d’) eje.plot_surface(X, y, resultados, cmap=‘chorro’) # mostrar la trama pyplot.show() |
La ejecución del ejemplo crea el gráfico de superficie de la función Ackley que muestra la gran cantidad de óptimos locales.

Gráfico de superficie 3D de la función multimodal de Ackley
Generaremos soluciones candidatas aleatorias, así como versiones modificadas de soluciones candidatas existentes. Es importante que todas las soluciones candidatas estén dentro de los límites del problema de búsqueda.
Para lograr esto, desarrollaremos una función para verificar si una solución candidata está dentro de los límites de la búsqueda y luego la descartaremos y generaremos otra solución si no lo está.
los in_bounds () La función siguiente tomará una solución candidata (punto) y la definición de los límites del espacio de búsqueda (límites) y devolverá Verdadero si la solución está dentro de los límites de la búsqueda o Falso en caso contrario.
|
# comprobar si un punto está dentro de los límites de la búsqueda def in_bounds(punto, límites): # enumere todas las dimensiones del punto por D en abarcar(len(límites)): # comprobar si está fuera de los límites de esta dimensión si punto[[D] < límites[[D, 0] o punto[[D] > límites[[D, 1]: regreso Falso regreso Cierto |
Luego podemos usar esta función al generar la población inicial de «justicia» (p.ej. lambda) soluciones candidatas aleatorias.
Por ejemplo:
|
... # población inicial población = lista() por _ en abarcar(justicia): candidato = Ninguno mientras candidato es Ninguno o no in_bounds(candidato, límites): candidato = límites[[:, 0] + rand(len(límites)) * (límites[[:, 1] – límites[[:, 0]) población.adjuntar(candidato) |
A continuación, podemos iterar sobre un número fijo de iteraciones del algoritmo. Cada iteración implica primero evaluar cada solución candidata en la población.
Calcularemos las puntuaciones y las almacenaremos en una lista paralela separada.
|
... # evaluar la aptitud de la población puntuaciones = [[objetivo(C) por C en población] |
A continuación, debemos seleccionar «muLos padres con las mejores puntuaciones, las más bajas en este caso, ya que estamos minimizando la función objetivo.
Haremos esto en dos pasos. Primero, clasificaremos las soluciones candidatas en función de sus puntajes en orden ascendente, de modo que la solución con el puntaje más bajo tenga un rango de 0, la siguiente tenga un rango de 1, y así sucesivamente. Podemos usar una doble llamada de la función argsort para lograr esto.
Luego usaremos los rangos y seleccionaremos aquellos padres que tengan un rango por debajo del valor «mu. » Esto significa que si mu se establece en 5 para seleccionar 5 padres, solo se seleccionarán aquellos padres con un rango entre 0 y 4.
|
... # clasifique las puntuaciones en orden ascendente rangos = argsort(argsort(puntuaciones)) # seleccione los índices para las mejores soluciones clasificadas por mu seleccionado = [[I por I,_ en enumerar(rangos) si rangos[[I] < mu] |
Luego podemos crear hijos para cada padre seleccionado.
Primero, debemos calcular el número total de hijos a crear por padre.
|
... # calcular el número de hijos por padre n_niños = En t(justicia / mu) |
Luego podemos iterar sobre cada padre y crear versiones modificadas de cada uno.
Crearemos niños utilizando una técnica similar a la utilizada en la escalada estocástica. Específicamente, cada variable se muestreará utilizando una distribución gaussiana con el valor actual como la media y la desviación estándar proporcionada como «Numero de pie”Hiperparámetro.
|
... # crear hijos para padres por _ en abarcar(n_niños): niño = Ninguno mientras niño es Ninguno o no in_bounds(niño, límites): niño = población[[I] + randn(len(límites)) * Numero de pie |
También podemos comprobar si cada padre seleccionado es mejor que la mejor solución vista hasta ahora para poder devolver la mejor solución al final de la búsqueda.
|
... # compruebe si este padre es la mejor solución jamás vista si puntuaciones[[I] < best_eval: mejor, best_eval = población[[I], puntuaciones[[I] imprimir(‘% d, mejor: f (% s) =% .5f’ % (época, mejor, best_eval)) |
Los hijos creados se pueden agregar a una lista y podemos reemplazar la población con la lista de hijos al final de la iteración del algoritmo.
|
... # reemplazar población con niños población = niños |
Podemos unir todo esto en una función llamada es_comma () que realiza la versión en coma del algoritmo de estrategia de evolución.
La función toma el nombre de la función objetivo, los límites del espacio de búsqueda, el número de iteraciones, el tamaño del paso y los hiperparámetros mu y lambda y devuelve la mejor solución encontrada durante la búsqueda y su evaluación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
# algoritmo de estrategia de evolución (mu, lambda) def es_comma(objetivo, límites, nitro, Numero de pie, mu, justicia): mejor, best_eval = Ninguno, 1e+10 # calcular el número de hijos por padre n_niños = En t(justicia / mu) # población inicial población = lista() por _ en abarcar(justicia): candidato = Ninguno mientras candidato es Ninguno o no in_bounds(candidato, límites): candidato = límites[[:, 0] + rand(len(límites)) * (límites[[:, 1] – límites[[:, 0]) población.adjuntar(candidato) # realizar la búsqueda por época en abarcar(nitro): # evaluar la aptitud de la población puntuaciones = [[objetivo(C) por C en población] # clasifique las puntuaciones en orden ascendente rangos = argsort(argsort(puntuaciones)) # seleccione los índices para las mejores soluciones clasificadas por mu seleccionado = [[I por I,_ en enumerar(rangos) si rangos[[I] < mu] # crear hijos de los padres niños = lista() por I en seleccionado: # compruebe si este padre es la mejor solución jamás vista si puntuaciones[[I] < best_eval: mejor, best_eval = población[[I], puntuaciones[[I] imprimir(‘% d, mejor: f (% s) =% .5f’ % (época, mejor, best_eval)) # crear hijos para padres por _ en abarcar(n_niños): niño = Ninguno mientras niño es Ninguno o no in_bounds(niño, límites): niño = población[[I] + randn(len(límites)) * Numero de pie niños.adjuntar(niño) # reemplazar población con niños población = niños regreso [[mejor, best_eval] |
A continuación, podemos aplicar este algoritmo a nuestra función objetivo de Ackley.
Ejecutaremos el algoritmo para 5000 iteraciones y usaremos un tamaño de paso de 0.15 en el espacio de búsqueda. Usaremos un tamaño de población (lambda) de 100 padres seleccionados de 20 (mu). Estos hiperparámetros se eligieron después de un poco de prueba y error.
Al final de la búsqueda, informaremos la mejor solución candidata encontrada durante la búsqueda.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 |
... # semilla del generador de números pseudoaleatorios semilla(1) # definir rango para entrada límites = asarray([[[[–5,0, 5,0], [[–5,0, 5,0]]) # definir las iteraciones totales nitro = 5000 # definir el tamaño máximo de paso Numero de pie = 0,15 # número de padres seleccionados mu = 20 # el número de hijos generados por los padres justicia = 100 # realizar la búsqueda de la estrategia de evolución (mu, lambda) mejor, puntaje = es_comma(objetivo, límites, nitro, Numero de pie, mu, justicia) imprimir(‘¡Hecho!’) imprimir(‘f (% s) =% f’ % (mejor, puntaje)) |
Al unir esto, el ejemplo completo de la aplicación de la versión en coma del algoritmo Evolution Strategies a la función objetivo de Ackley se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 sesenta y cinco 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 |
# estrategia de evolución (mu, lambda) de la función objetivo de ackley desde numpy importar asarray desde numpy importar Exp desde numpy importar sqrt desde numpy importar porque desde numpy importar mi desde numpy importar Pi desde numpy importar argsort desde numpy.aleatorio importar randn desde numpy.aleatorio importar rand desde numpy.aleatorio importar semilla # función objetiva def objetivo(v): X, y = v regreso –20,0 * Exp(–0,2 * sqrt(0,5 * (X**2 + y **2))) – Exp(0,5 * (porque(2 * Pi * X) + porque(2 * Pi * y))) + mi + 20 # comprobar si un punto está dentro de los límites de la búsqueda def in_bounds(punto, límites): # enumere todas las dimensiones del punto por D en abarcar(len(límites)): # comprobar si está fuera de los límites de esta dimensión si punto[[D] < límites[[D, 0] o punto[[D] > límites[[D, 1]: regreso Falso regreso Cierto # algoritmo de estrategia de evolución (mu, lambda) def es_comma(objetivo, límites, nitro, Numero de pie, mu, justicia): mejor, best_eval = Ninguno, 1e+10 # calcular el número de hijos por padre n_niños = En t(justicia / mu) # población inicial población = lista() por _ en abarcar(justicia): candidato = Ninguno mientras candidato es Ninguno o no in_bounds(candidato, límites): candidato = límites[[:, 0] + rand(len(límites)) * (límites[[:, 1] – límites[[:, 0]) población.adjuntar(candidato) # realizar la búsqueda por época en abarcar(nitro): # evaluar la aptitud de la población puntuaciones = [[objetivo(C) por C en población] # clasifique las puntuaciones en orden ascendente rangos = argsort(argsort(puntuaciones)) # seleccione los índices para las mejores soluciones clasificadas por mu seleccionado = [[I por I,_ en enumerar(rangos) si rangos[[I] < mu] # crear hijos de los padres niños = lista() por I en seleccionado: # compruebe si este padre es la mejor solución jamás vista si puntuaciones[[I] < best_eval: mejor, best_eval = población[[I], puntuaciones[[I] imprimir(‘% d, mejor: f (% s) =% .5f’ % (época, mejor, best_eval)) # crear hijos para padres por _ en abarcar(n_niños): niño = Ninguno mientras niño is Ninguno o not in_bounds(child, bounds): child = population[[i] + randn(len(bounds)) * step_size children.append(child) # replace population with children population = children return [[mejor, best_eval] # seed the pseudorandom number generator seed(1) # define range for input bounds = asarray([[[[–5.0, 5.0], [[–5.0, 5.0]]) # define the total iterations n_iter = 5000 # define the maximum step size step_size = 0.15 # number of parents selected mu = 20 # the number of children generated by parents lam = 100 # perform the evolution strategy (mu, lambda) search mejor, score = es_comma(objective, bounds, n_iter, step_size, mu, lam) imprimir(‘Done!’) imprimir(‘f(%s) = %f’ % (mejor, score)) |
Running the example reports the candidate solution and scores each time a better solution is found, then reports the best solution found at the end of the search.
Nota: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, we can see that about 22 improvements to performance were seen during the search and the best solution is close to the optima.
No doubt, this solution can be provided as a starting point to a local search algorithm to be further refined, a common practice when using a global optimization algorithm like ES.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 |
0, Best: f([-0.82977995 2.20324493]) = 6.91249 0, Best: f([-1.03232526 0.38816734]) = 4.49240 1, Best: f([-1.02971385 0.21986453]) = 3.68954 2, Best: f([-0.98361735 0.19391181]) = 3.40796 2, Best: f([-0.98189724 0.17665892]) = 3.29747 2, Best: f([-0.07254927 0.67931431]) = 3.29641 3, Best: f([-0.78716147 0.02066442]) = 2.98279 3, Best: f([-1.01026218 -0.03265665]) = 2.69516 3, Best: f([-0.08851828 0.26066485]) = 2.00325 4, Best: f([-0.23270782 0.04191618]) = 1.66518 4, Best: f([-0.01436704 0.03653578]) = 0.15161 7, Best: f([0.01247004 0.01582657]) = 0.06777 9, Best: f([0.00368129 0.00889718]) = 0.02970 25, Best: f([ 0.00666975 -0.0045051 ]) = 0.02449 33, Best: f([-0.00072633 -0.00169092]) = 0.00530 211, Best: f([2.05200123e-05 1.51343187e-03]) = 0.00434 315, Best: f([ 0.00113528 -0.00096415]) = 0.00427 418, Best: f([ 0.00113735 -0.00030554]) = 0.00337 491, Best: f([ 0.00048582 -0.00059587]) = 0.00219 704, Best: f([-6.91643854e-04 -4.51583644e-05]) = 0.00197 1504, Best: f([ 2.83063223e-05 -4.60893027e-04]) = 0.00131 3725, Best: f([ 0.00032757 -0.00023643]) = 0.00115 Done! f([ 0.00032757 -0.00023643]) = 0.001147 |
Now that we are familiar with how to implement the comma version of evolution strategies, let’s look at how we might implement the plus version.
Develop a (mu + lambda)-ES
The plus version of the Evolution Strategies algorithm is very similar to the comma version.
The main difference is that children and the parents comprise the population at the end instead of just the children. This allows the parents to compete with the children for selection in the next iteration of the algorithm.
This can result in a more greedy behavior by the search algorithm and potentially premature convergence to local optima (suboptimal solutions). The benefit is that the algorithm is able to exploit good candidate solutions that were found and focus intently on candidate solutions in the region, potentially finding further improvements.
We can implement the plus version of the algorithm by modifying the function to add parents to the population when creating the children.
|
... # keep the parent children.append(population[[i]) |
The updated version of the function with this addition, and with a new name es_plus() , is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
# evolution strategy (mu + lambda) algorithm def es_plus(objective, bounds, n_iter, step_size, mu, lam): mejor, best_eval = Ninguno, 1e+10 # calculate the number of children per parent n_children = int(lam / mu) # initial population population = list() for _ en range(lam): candidate = Ninguno while candidate is Ninguno o not in_bounds(candidate, bounds): candidate = bounds[[:, 0] + rand(len(bounds)) * (bounds[[:, 1] – bounds[[:, 0]) population.append(candidate) # perform the search for epoch en range(n_iter): # evaluate fitness for the population scores = [[objective(c) for c en population] # rank scores in ascending order ranks = argsort(argsort(scores)) # select the indexes for the top mu ranked solutions selected = [[i for i,_ en enumerate(ranks) if ranks[[i] < mu] # create children from parents children = list() for i en selected: # check if this parent is the best solution ever seen if scores[[i] < best_eval: mejor, best_eval = population[[i], scores[[i] imprimir(‘%d, Best: f(%s) = %.5f’ % (epoch, mejor, best_eval)) # keep the parent children.append(population[[i]) # create children for parent for _ en range(n_children): child = Ninguno while child is Ninguno o not in_bounds(child, bounds): child = population[[i] + randn(len(bounds)) * step_size children.append(child) # replace population with children population = children return [[mejor, best_eval] |
We can apply this version of the algorithm to the Ackley objective function with the same hyperparameters used in the previous section.
The complete example is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 |
# evolution strategy (mu + lambda) of the ackley objective function desde numpy import asarray desde numpy import exp desde numpy import sqrt desde numpy import cos desde numpy import mi desde numpy import pi desde numpy import argsort desde numpy.random import randn desde numpy.random import rand desde numpy.random import seed # objective function def objective(v): x, y = v return –20.0 * exp(–0.2 * sqrt(0.5 * (x**2 + y**2))) – exp(0.5 * (cos(2 * pi * x) + cos(2 * pi * y))) + mi + 20 # check if a point is within the bounds of the search def in_bounds(point, bounds): # enumerate all dimensions of the point for D en range(len(bounds)): # check if out of bounds for this dimension if point[[D] < bounds[[D, 0] o point[[D] > bounds[[D, 1]: return False return True # evolution strategy (mu + lambda) algorithm def es_plus(objective, bounds, n_iter, step_size, mu, lam): mejor, best_eval = Ninguno, 1e+10 # calculate the number of children per parent n_children = int(lam / mu) # initial population population = list() for _ en range(lam): candidate = Ninguno while candidate is Ninguno o not in_bounds(candidate, bounds): candidate = bounds[[:, 0] + rand(len(bounds)) * (bounds[[:, 1] – bounds[[:, 0]) population.append(candidate) # perform the search for epoch en range(n_iter): # evaluate fitness for the population scores = [[objective(c) for c en population] # rank scores in ascending order ranks = argsort(argsort(scores)) # select the indexes for the top mu ranked solutions selected = [[i for i,_ en enumerate(ranks) if ranks[[i] < mu] # create children from parents children = list() for i en selected: # check if this parent is the best solution ever seen if scores[[i] < best_eval: mejor, best_eval = population[[i], scores[[i] imprimir(‘%d, Best: f(%s) = %.5f’ % (epoch, mejor, best_eval)) # keep the parent children.append(population[[i]) # create children for parent for _ en range(n_children): child = Ninguno while child is Ninguno o not in_bounds(child, bounds): child = population[[i] + randn(len(bounds)) * step_size children.append(child) # replace population with children population = children return [[mejor, best_eval] # seed the pseudorandom number generator seed(1) # define range for input bounds = asarray([[[[–5.0, 5.0], [[–5.0, 5.0]]) # define the total iterations n_iter = 5000 # define the maximum step size step_size = 0.15 # number of parents selected mu = 20 # the number of children generated by parents lam = 100 # perform the evolution strategy (mu + lambda) search mejor, score = es_plus(objective, bounds, n_iter, step_size, mu, lam) imprimir(‘Done!’) imprimir(‘f(%s) = %f’ % (mejor, score)) |
Running the example reports the candidate solution and scores each time a better solution is found, then reports the best solution found at the end of the search.
Nota: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, we can see that about 24 improvements to performance were seen during the search. We can also see that a better final solution was found with an evaluation of 0.000532, compared to 0.001147 found with the comma version on this objective function.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 |
0, Best: f([-0.82977995 2.20324493]) = 6.91249 0, Best: f([-1.03232526 0.38816734]) = 4.49240 1, Best: f([-1.02971385 0.21986453]) = 3.68954 2, Best: f([-0.96315064 0.21176994]) = 3.48942 2, Best: f([-0.9524528 -0.19751564]) = 3.39266 2, Best: f([-1.02643442 0.14956346]) = 3.24784 2, Best: f([-0.90172166 0.15791013]) = 3.17090 2, Best: f([-0.15198636 0.42080645]) = 3.08431 3, Best: f([-0.76669476 0.03852254]) = 3.06365 3, Best: f([-0.98979547 -0.01479852]) = 2.62138 3, Best: f([-0.10194792 0.33439734]) = 2.52353 3, Best: f([0.12633886 0.27504489]) = 2.24344 4, Best: f([-0.01096566 0.22380389]) = 1.55476 4, Best: f([0.16241469 0.12513091]) = 1.44068 5, Best: f([-0.0047592 0.13164993]) = 0.77511 5, Best: f([ 0.07285478 -0.0019298 ]) = 0.34156 6, Best: f([-0.0323925 -0.06303525]) = 0.32951 6, Best: f([0.00901941 0.0031937 ]) = 0.02950 32, Best: f([ 0.00275795 -0.00201658]) = 0.00997 109, Best: f([-0.00204732 0.00059337]) = 0.00615 195, Best: f([-0.00101671 0.00112202]) = 0.00434 555, Best: f([ 0.00020392 -0.00044394]) = 0.00139 2804, Best: f([3.86555110e-04 6.42776651e-05]) = 0.00111 4357, Best: f([ 0.00013889 -0.0001261 ]) = 0.00053 Done! f([ 0.00013889 -0.0001261 ]) = 0.000532 |
Further Reading
This section provides more resources on the topic if you are looking to go deeper.
Papers
Books
Articles
Resumen
In this tutorial, you discovered how to implement the evolution strategies optimization algorithm.
Specifically, you learned:
- Evolution Strategies is a stochastic global optimization algorithm inspired by the biological theory of evolution by natural selection.
- There is a standard terminology for Evolution Strategies and two common versions of the algorithm referred to as (mu, lambda)-ES and (mu + lambda)-ES.
- How to implement and apply the Evolution Strategies algorithm to continuous objective functions.
Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.
