Escalada de la colina estocástica es un algoritmo de optimización.
Hace uso de la aleatoriedad como parte del proceso de búsqueda. Esto hace que el algoritmo sea apropiado para funciones objetivas no lineales donde otros algoritmos de búsqueda locales no funcionan bien.
También es un algoritmo de búsqueda local, lo que significa que modifica una solución única y busca el área relativamente local del espacio de búsqueda hasta que se localiza el óptimo local. Esto significa que es apropiado para problemas de optimización unimodal o para su uso después de la aplicación de un algoritmo de optimización global.
En este tutorial, descubrirá el algoritmo de optimización de escalada para la optimización de funciones
Después de completar este tutorial, lo sabrás:
- La escalada de colinas es un algoritmo de búsqueda local estocástico para la optimización de funciones.
- Cómo implementar el algoritmo de escalada de colinas desde cero en Python.
- Cómo aplicar el algoritmo de escalada de colinas e inspeccionar los resultados del algoritmo.
Empecemos.

Escalada de la colina estocástica en Python desde cero
Foto de John, algunos derechos reservados.
Resumen del Tutorial
Este tutorial está dividido en tres partes; son:
- Algoritmo de escalada de colinas
- Aplicación del algoritmo de escalada de colinas
- Ejemplo de aplicación del algoritmo de escalada de colinas
Algoritmo de escalada de colinas
El algoritmo de escalada de colinas estocástico es un algoritmo de optimización de búsqueda local estocástico.
Toma un punto inicial como entrada y un tamaño de paso, donde el tamaño de paso es una distancia dentro del espacio de búsqueda.
El algoritmo toma el punto inicial como la mejor solución candidata actual y genera un nuevo punto dentro de la distancia de tamaño de paso del punto proporcionado. Se evalúa el punto generado, y si es igual o mejor que el punto actual, se toma como el punto actual.
La generación del nuevo punto utiliza la aleatoriedad, a menudo conocida como escalada de colinas estocástica. Esto significa que el algoritmo puede saltar sobre regiones accidentadas, ruidosas, discontinuas o engañosas de la superficie de respuesta como parte de la búsqueda.
La escalada de colinas estocásticas elige al azar entre los movimientos de subida; la probabilidad de selección puede variar con la inclinación del movimiento de subida.
– Página 124, Inteligencia Artificial: Un enfoque moderno, 2009.
Es importante que se acepten diferentes puntos con igual evaluación ya que permite al algoritmo continuar explorando el espacio de búsqueda, por ejemplo a través de regiones planas de la superficie de respuesta. También puede ser útil poner un límite a estas llamadas «de lado«se mueve para evitar un bucle infinito.
Si siempre permitimos movimientos laterales cuando no hay movimientos cuesta arriba, se producirá un bucle infinito cuando el algoritmo alcance un máximo local plano que no sea un hombro. Una solución común es poner un límite al número de movimientos laterales consecutivos permitidos. Por ejemplo, podríamos permitir hasta, digamos, 100 movimientos laterales consecutivos
– Página 123, Inteligencia Artificial: Un enfoque moderno, 2009.
Este proceso continúa hasta que se cumple una condición de parada, como un número máximo de evaluaciones de la función o ninguna mejora dentro de un número determinado de evaluaciones de la función.
El algoritmo toma su nombre del hecho de que subirá (estocásticamente) la colina de la superficie de respuesta al óptico local. Esto no significa que sólo pueda utilizarse para maximizar las funciones objetivas; es sólo un nombre. De hecho, típicamente, minimizamos las funciones en lugar de maximizarlas.
El algoritmo de búsqueda de subida de colinas (versión más empinada) […] es simplemente un bucle que se mueve continuamente en la dirección del aumento del valor, es decir, cuesta arriba. Termina cuando alcanza un «pico» donde ningún vecino tiene un valor más alto.
– Página 122, Inteligencia Artificial: Un enfoque moderno, 2009.
Como algoritmo de búsqueda local, puede atascarse en el óptimo local. Sin embargo, los reinicios múltiples pueden permitir al algoritmo localizar el óptimo global.
La escalada de la colina al azar… […] lleva a cabo una serie de búsquedas de escalada desde los estados iniciales generados aleatoriamente, hasta que se encuentra un objetivo.
– Página 124, Inteligencia Artificial: Un enfoque moderno, 2009.
El tamaño del paso debe ser lo suficientemente grande como para permitir localizar mejores puntos cercanos en el espacio de búsqueda, pero no tan grande como para que la búsqueda salte fuera de la región que contiene el óptico local.
Aplicación del algoritmo de escalada de colinas
En el momento de escribir este artículo, la biblioteca de SciPy no ofrece una implementación de la escalada estocástica de colinas.
Sin embargo, podemos implementarlo nosotros mismos.
Primero, debemos definir nuestra función objetiva y los límites de cada variable de entrada a la función objetiva. La función objetivo es sólo una función de Python que nombraremos objetivo(). Los límites serán una matriz 2D con una dimensión para cada variable de entrada que define el mínimo y el máximo de la variable.
Por ejemplo, una función objetiva unidimensional y los límites se definirían de la siguiente manera:
|
# Función objetiva def objetivo(x): volver 0 # Definir el rango de entrada bounds = asarray([[[[–5.0, 5.0]]) |
A continuación, podemos generar nuestra solución inicial como un punto aleatorio dentro de los límites del problema, y luego evaluarla usando la función objetivo.
|
... # Generar un punto inicial solución = bounds[[:, 0] + rand(len(bounds)) * (bounds[[:, 1] – bounds[[:, 0]) # Evaluar el punto inicial solution_eval = objetivo(solución) |
Ahora podemos hacer un bucle sobre un número predefinido de iteraciones del algoritmo definido como «n_iteraciones«, como 100 o 1.000.
|
... # Corre la subida de la colina para i en rango(n_iteraciones): ... |
El primer paso de la iteración del algoritmo es dar un paso.
Esto requiere una predefinida «tamaño_paso«que es relativo a los límites del espacio de búsqueda. Daremos un paso aleatorio con una distribución Gaussiana donde la media es nuestro punto actual y la desviación estándar está definida por el parámetro «tamaño_paso“. Eso significa que alrededor del 99 por ciento de los pasos dados estarán dentro de (3 * tamaño_paso) del punto actual.
|
... # dar un paso candidato = solución + randn(len(bounds)) * tamaño_paso |
No tenemos que tomar medidas de esta manera. Tal vez quiera usar una distribución uniforme entre 0 y el tamaño del paso. Por ejemplo:
|
... # dar un paso candidato = solución + rand(len(bounds)) * tamaño_paso |
A continuación tenemos que evaluar la nueva solución candidata con la función objetivo.
|
... # Evaluar el punto de candidato candidata_eval = objetivo(candidato) |
Entonces tenemos que comprobar si la evaluación de este nuevo punto es tan buena o mejor que el mejor punto actual, y si lo es, reemplazar nuestro mejor punto actual con este nuevo punto.
|
... # comprobar si debemos mantener el nuevo punto si candidata_eval <= solution_eval: # Almacena el nuevo punto solución, solution_eval = candidato, candidato_eval # Reportar el progreso… imprimir(‘>%d f(%s) = %.5f’ % (i, solución, solution_eval)) |
Y eso es todo.
Podemos implementar este algoritmo de escalada de colinas como una función reutilizable que toma el nombre de la función objetivo, los límites de cada variable de entrada, el total de iteraciones y pasos como argumentos, y devuelve la mejor solución encontrada y su evaluación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# Algoritmo de búsqueda local de escalada de colinas def escalada(objetivo, bounds, n_iteraciones, tamaño_paso): # Generar un punto inicial solución = bounds[[:, 0] + rand(len(bounds)) * (bounds[[:, 1] – bounds[[:, 0]) # Evaluar el punto inicial solution_eval = objetivo(solución) # Corre la subida de la colina para i en rango(n_iteraciones): # dar un paso candidato = solución + randn(len(bounds)) * paso_tamaño # Evaluar el punto de candidato candidata_eval = objetivo(candidato) # comprobar si debemos mantener el nuevo punto si candidata_eval <= solution_eval: # Almacena el nuevo punto solución, solution_eval = candidato, candidato_eval # Reportar el progreso… imprimir(‘>%d f(%s) = %.5f’ % (i, solución, solution_eval)) volver [[solución, solution_eval] |
Ahora que sabemos cómo implementar el algoritmo de escalada de colinas en Python, veamos cómo podríamos usarlo para optimizar una función objetiva.
Ejemplo de aplicación del algoritmo de escalada de colinas
En esta sección, aplicaremos el algoritmo de optimización de escalada a una función objetiva.
Primero, definamos nuestra función objetiva.
Usaremos una simple función objetiva unidimensional x^2 con los límites [-5, 5].
El ejemplo que se presenta a continuación define la función, luego crea un diagrama de líneas de la superficie de respuesta de la función para una cuadrícula de valores de entrada y marca el óptimo en f(0,0) = 0,0 con una línea roja.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
# Función de optimización unimodal convexa de numpy importación arange de matplotlib importación pyplot # Función objetiva def objetivo(x): volver x[[0]**2.0 # Definir el rango de entrada r_min, r_max = –5.0, 5.0 # Rango de entrada de la muestra uniformemente en incrementos de 0.1 aportaciones = arange(r_min, r_max, 0.1) # computar los objetivos resultados = [[objetivo([[x]) para x en aportaciones] # Crear un gráfico de líneas de entrada vs. resultado pyplot.parcela(aportaciones, resultados) # Definir el valor óptimo de entrada x_optima = 0.0 # Dibujar una línea vertical en la entrada óptima pyplot.axvline(x=x_optima, ls=‘–‘, color=«rojo) # mostrar la trama pyplot.mostrar() |
La ejecución del ejemplo crea un trazado lineal de la función objetivo y marca claramente la función óptima.
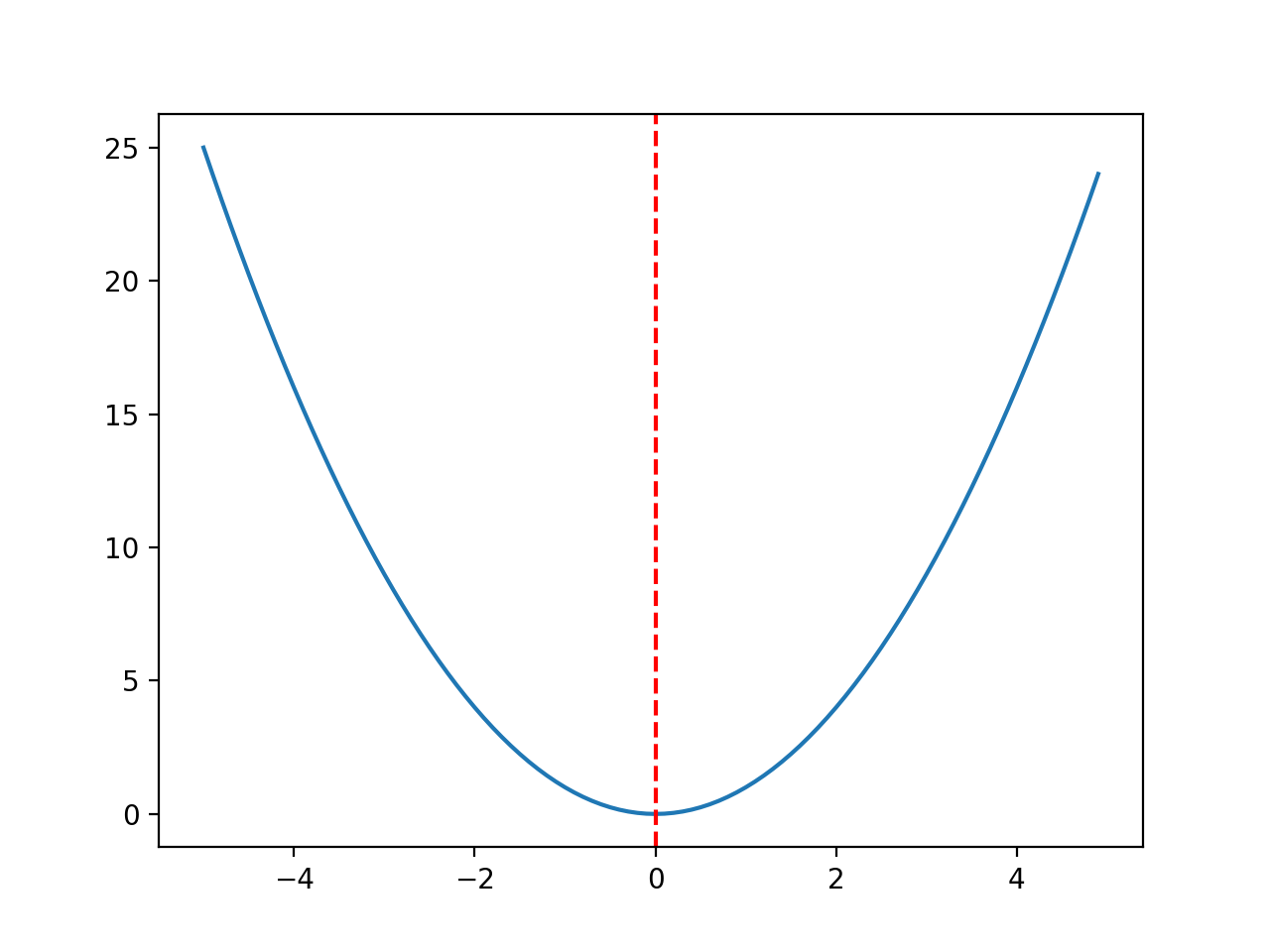
Trazado de la función del objetivo con el Óptimo marcado con una línea roja discontinua
A continuación, podemos aplicar el algoritmo de escalada de colinas a la función objetivo.
Primero, sembraremos el generador de números pseudoaleatorios. Esto no es necesario en general, pero en este caso, quiero asegurarme de que obtenemos los mismos resultados (la misma secuencia de números aleatorios) cada vez que ejecutamos el algoritmo para poder graficar los resultados más tarde.
|
... # Sembrar el generador de números pseudoaleatorios semilla(5) |
A continuación, podemos definir la configuración de la búsqueda.
En este caso, buscaremos 1.000 iteraciones del algoritmo y usaremos un tamaño de paso de 0,1. Dado que estamos utilizando una función gaussiana para generar el paso, esto significa que alrededor del 99 por ciento de todos los pasos dados estarán dentro de una distancia de (0,1 * 3) de un punto dado, por ejemplo, tres desviaciones estándar.
|
... n_iteraciones = 1000 # Definir el tamaño máximo del paso tamaño_paso = 0.1 |
A continuación, podemos realizar la búsqueda y reportar los resultados.
|
... # realizar la búsqueda de la escalada de la colina mejor, puntuación = escalada(objetivo, bounds, n_iteraciones, tamaño_paso) imprimir(«¡Hecho!) imprimir(«f(%s) = %f % (mejor, puntuación)) |
Acoplando todo esto, el ejemplo completo se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
# Subir una colina en busca de una función objetiva unidimensional de numpy importación asarray de numpy.al azar importación randn de numpy.al azar importación rand de numpy.al azar importación semilla # Función objetiva def objetivo(x): volver x[[0]**2.0 # Algoritmo de búsqueda local de escalada de colinas def escalada(objetivo, bounds, n_iteraciones, tamaño_paso): # Generar un punto inicial solución = bounds[[:, 0] + rand(len(bounds)) * (bounds[[:, 1] – bounds[[:, 0]) # Evaluar el punto inicial solution_eval = objetivo(solución) # Corre la subida de la colina para i en rango(n_iteraciones): # dar un paso candidato = solución + randn(len(bounds)) * paso_tamaño # Evaluar el punto de candidato candidata_eval = objetivo(candidato) # comprobar si debemos mantener el nuevo punto si candidata_eval <= solution_eval: # Almacena el nuevo punto solución, solution_eval = candidato, candidato_eval # Reportar el progreso… imprimir(‘>%d f(%s) = %.5f’ % (i, solución, solution_eval)) volver [[solución, solution_eval] # Sembrar el generador de números pseudoaleatorios semilla(5) # Definir el rango de entrada bounds = asarray([[[[–5.0, 5.0]]) # Definir las iteraciones totales n_iteraciones = 1000 # Definir el tamaño máximo del paso tamaño_paso = 0.1 # realizar la búsqueda de la escalada de la colina mejor, puntuación = escalada(objetivo, bounds, n_iteraciones, tamaño_paso) imprimir(«¡Hecho!) imprimir(«f(%s) = %f % (mejor, puntuación)) |
La ejecución del ejemplo informa del progreso de la búsqueda, incluyendo el número de iteración, la entrada de la función y la respuesta de la función objetiva cada vez que se detecta una mejora.
Al final de la búsqueda, se encuentra la mejor solución y se informa de su evaluación.
En este caso podemos ver alrededor de 36 mejoras sobre las 1.000 iteraciones del algoritmo y una solución que está muy cerca de la entrada óptima de 0,0 que evalúa a f(0,0) = 0,0.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
>1 f([-2.74290923]) = 7.52355 >3 f([-2.65873147]) = 7.06885 >4 f([-2.52197291]) = 6.36035 >5 f([-2.46450214]) = 6.07377 >7 f([-2.44740961]) = 5.98981 >9 f([-2.28364676]) = 5.21504 >12 f([-2.19245939]) = 4.80688 >14 f([-2.01001538]) = 4.04016 >15 f([-1.86425287]) = 3.47544 >22 f([-1.79913002]) = 3.23687 >24 f([-1.57525573]) = 2.48143 >25 f([-1.55047719]) = 2.40398 >26 f([-1.51783757]) = 2.30383 >27 f([-1.49118756]) = 2.22364 >28 f([-1.45344116]) = 2.11249 >30 f([-1.33055275]) = 1.77037 >32 f([-1.17805016]) = 1.38780 >33 f([-1.15189314]) = 1.32686 >36 f([-1.03852644]) = 1.07854 >37 f([-0.99135322]) = 0.98278 >38 f([-0.79448984]) = 0.63121 >39 f([-0.69837955]) = 0.48773 >42 f([-0.69317313]) = 0.48049 >46 f([-0.61801423]) = 0.38194 >48 f([-0.48799625]) = 0.23814 >50 f([-0.22149135]) = 0.04906 >54 f([-0.20017144]) = 0.04007 >57 f([-0.15994446]) = 0.02558 >60 f([-0.15492485]) = 0.02400 >61 f([-0.03572481]) = 0.00128 >64 f([-0.03051261]) = 0.00093 >66 f([-0.0074283]) = 0.00006 >78 f([-0.00202357]) = 0.00000 >119 f([0.00128373]) = 0.00000 >120 f([-0.00040911]) = 0.00000 >314 f([-0.00017051]) = 0.00000 ¡Hecho! f([-0.00017051]) = 0.000000 |
Puede ser interesante revisar el progreso de la búsqueda como un gráfico de líneas que muestra el cambio en la evaluación de la mejor solución cada vez que hay una mejora.
Podemos actualizar el escalada de colinas() para hacer un seguimiento de las evaluaciones objetivas de la función cada vez que haya una mejora y devolver esta lista de puntuaciones.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
# Algoritmo de búsqueda local de escalada de colinas def escalada(objetivo, bounds, n_iteraciones, tamaño_paso): # Generar un punto inicial solución = bounds[[:, 0] + rand(len(bounds)) * (bounds[[:, 1] – bounds[[:, 0]) # Evaluar el punto inicial solution_eval = objetivo(solución) # Corre la subida de la colina resultados = lista() resultados.anexar(solution_eval) para i en rango(n_iteraciones): # dar un paso candidato = solución + randn(len(bounds)) * paso_tamaño # Evaluar el punto de candidato candidata_eval = objetivo(candidato) # comprobar si debemos mantener el nuevo punto si candidata_eval <= solution_eval: # Almacena el nuevo punto solución, solution_eval = candidato, candidato_eval # Llevar la cuenta de las puntuaciones resultados.anexar(solution_eval) # Reportar el progreso… imprimir(‘>%d f(%s) = %.5f’ % (i, solución, solution_eval)) volver [[solución, solution_eval, resultados] |
Podemos crear un gráfico de líneas de estas puntuaciones para ver el cambio relativo en la función objetivo para cada mejora encontrada durante la búsqueda.
|
... # Gráfica de línea de las mejores puntuaciones pyplot.parcela(resultados, ‘.-‘) pyplot.xlabel(«Número de la mejora) pyplot.ylabel(«Evaluación f(x)) pyplot.mostrar() |
Enlazando todo esto, a continuación se enumera el ejemplo completo de cómo realizar la búsqueda y trazar las puntuaciones de las funciones objetivas de las soluciones mejoradas durante la búsqueda.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 |
# Subir una colina en busca de una función objetiva unidimensional de numpy importación asarray de numpy.al azar importación randn de numpy.al azar importación rand de numpy.al azar importación semilla de matplotlib importación pyplot # Función objetiva def objetivo(x): volver x[[0]**2.0 # Algoritmo de búsqueda local de escalada de colinas def escalada(objetivo, bounds, n_iteraciones, tamaño_paso): # Generar un punto inicial solución = bounds[[:, 0] + rand(len(bounds)) * (bounds[[:, 1] – bounds[[:, 0]) # Evaluar el punto inicial solution_eval = objetivo(solución) # Corre la subida de la colina resultados = lista() resultados.anexar(solution_eval) para i en rango(n_iteraciones): # dar un paso candidato = solución + randn(len(bounds)) * paso_tamaño # Evaluar el punto de candidato candidata_eval = objetivo(candidato) # comprobar si debemos mantener el nuevo punto si candidata_eval <= solution_eval: # Almacena el nuevo punto solución, solution_eval = candidato, candidato_eval # Llevar la cuenta de las puntuaciones resultados.anexar(solution_eval) # Reportar el progreso… imprimir(‘>%d f(%s) = %.5f’ % (i, solución, solution_eval)) volver [[solución, solution_eval, resultados] # Sembrar el generador de números pseudoaleatorios semilla(5) # Definir el rango de entrada bounds = asarray([[[[–5.0, 5.0]]) # Definir las iteraciones totales n_iteraciones = 1000 # Definir el tamaño máximo del paso tamaño_paso = 0.1 # realizar la búsqueda de la escalada de la colina mejor, puntuación, resultados = escalada(objetivo, bounds, n_iteraciones, tamaño_paso) imprimir(«¡Hecho!) imprimir(«f(%s) = %f % (mejor, puntuación)) # Gráfica de línea de las mejores puntuaciones pyplot.parcela(resultados, ‘.-‘) pyplot.xlabel(«Número de la mejora) pyplot.ylabel(«Evaluación f(x)) pyplot.mostrar() |
Ejecutando el ejemplo se realiza la búsqueda y se reportan los resultados como antes.
Se crea un gráfico de líneas que muestra la evaluación de la función objetiva para cada mejora durante la búsqueda de la escalada de la colina. Podemos ver unos 36 cambios en la evaluación de la función objetiva durante la búsqueda, con grandes cambios inicialmente y cambios muy pequeños a imperceptibles hacia el final de la búsqueda a medida que el algoritmo convergió en el óptimo.
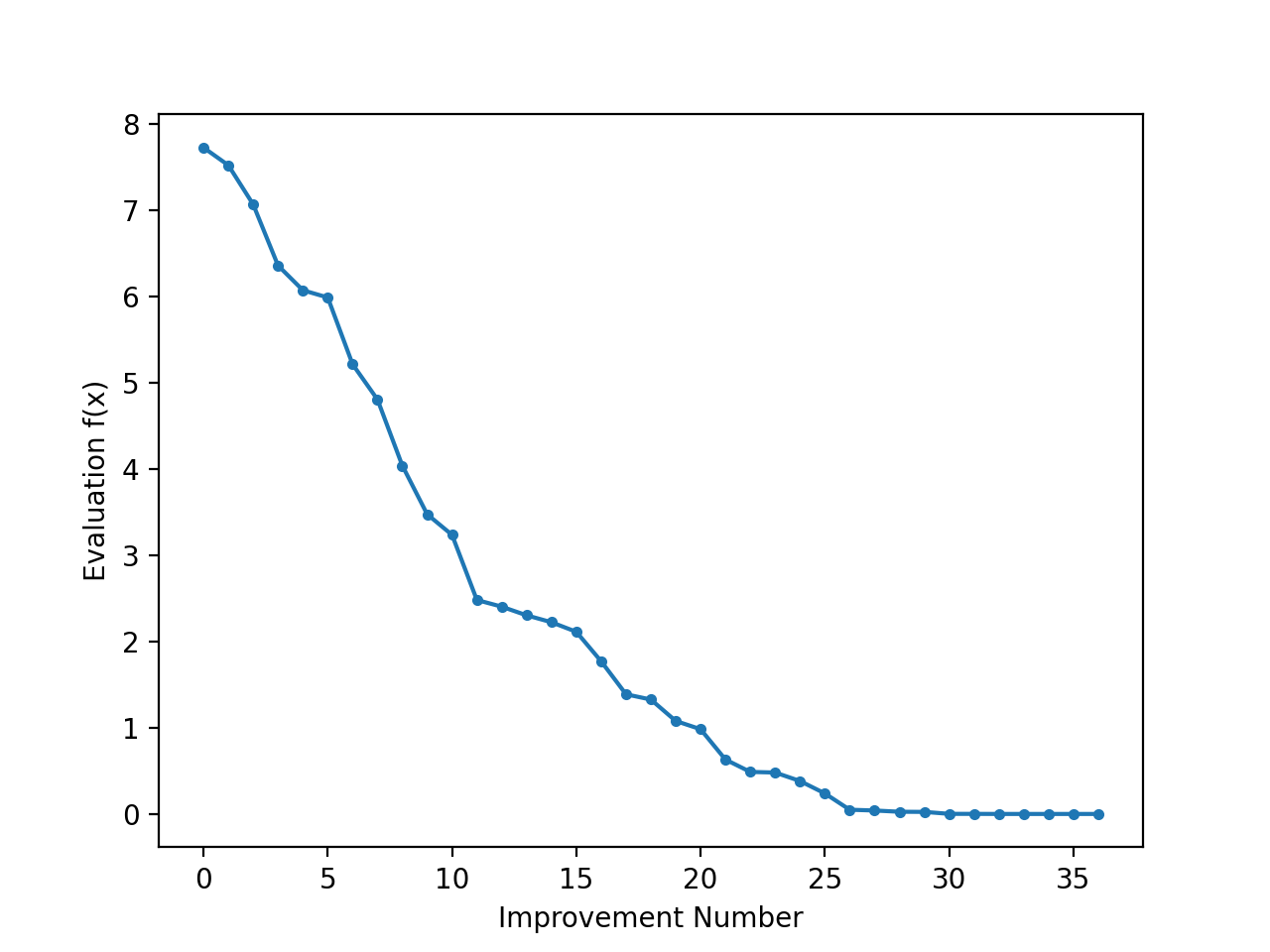
Gráfica de evaluación objetiva de la función para cada mejora durante la búsqueda de la escalada de la colina
Dado que la función del objetivo es unidimensional, es sencillo trazar la superficie de respuesta como hicimos anteriormente.
Puede ser interesante revisar el progreso de la búsqueda trazando las mejores soluciones candidatas encontradas durante la búsqueda como puntos en la superficie de respuesta. Se esperaría una secuencia de puntos que bajaran por la superficie de respuesta hasta el Óptimo.
Esto puede lograrse actualizando primero el escalada de colinas() para hacer un seguimiento de cada una de las mejores soluciones candidatas según se vayan localizando durante la búsqueda, y luego devolver una lista de las mejores soluciones.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
# Algoritmo de búsqueda local de escalada de colinas def escalada(objetivo, bounds, n_iteraciones, tamaño_paso): # Generar un punto inicial solución = bounds[[:, 0] + rand(len(bounds)) * (bounds[[:, 1] – bounds[[:, 0]) # Evaluar el punto inicial solution_eval = objetivo(solución) # Corre la subida de la colina soluciones = lista() soluciones.anexar(solución) para i en rango(n_iteraciones): # dar un paso candidato = solución + randn(len(bounds)) * paso_tamaño # Evaluar el punto de candidato candidata_eval = objetivo(candidato) # comprobar si debemos mantener el nuevo punto si candidata_eval <= solution_eval: # Almacena el nuevo punto solución, solution_eval = candidato, candidato_eval # mantener el seguimiento de las soluciones soluciones.anexar(solución) # Reportar el progreso… imprimir(‘>%d f(%s) = %.5f’ % (i, solución, solution_eval)) volver [[solución, solution_eval, soluciones] |
Podemos entonces crear un gráfico de la superficie de respuesta de la función objetivo y marcar el óptimo como antes.
|
... # Rango de entrada de la muestra uniformemente en incrementos de 0.1 aportaciones = arange(bounds[[0,0], bounds[[0,1], 0.1) # Crear un gráfico de líneas de entrada vs. resultado pyplot.parcela(aportaciones, [[objetivo([[x]) para x en aportaciones], ‘–‘) # Dibujar una línea vertical en la entrada óptima pyplot.axvline(x=[[0.0], ls=‘–‘, color=«rojo) |
Finalmente, podemos trazar la secuencia de soluciones candidatas encontradas por la búsqueda como puntos negros.
|
... # trazar la muestra como círculos negros pyplot.parcela(soluciones, [[objetivo(x) para x en soluciones], ‘o’, color=«negro) |
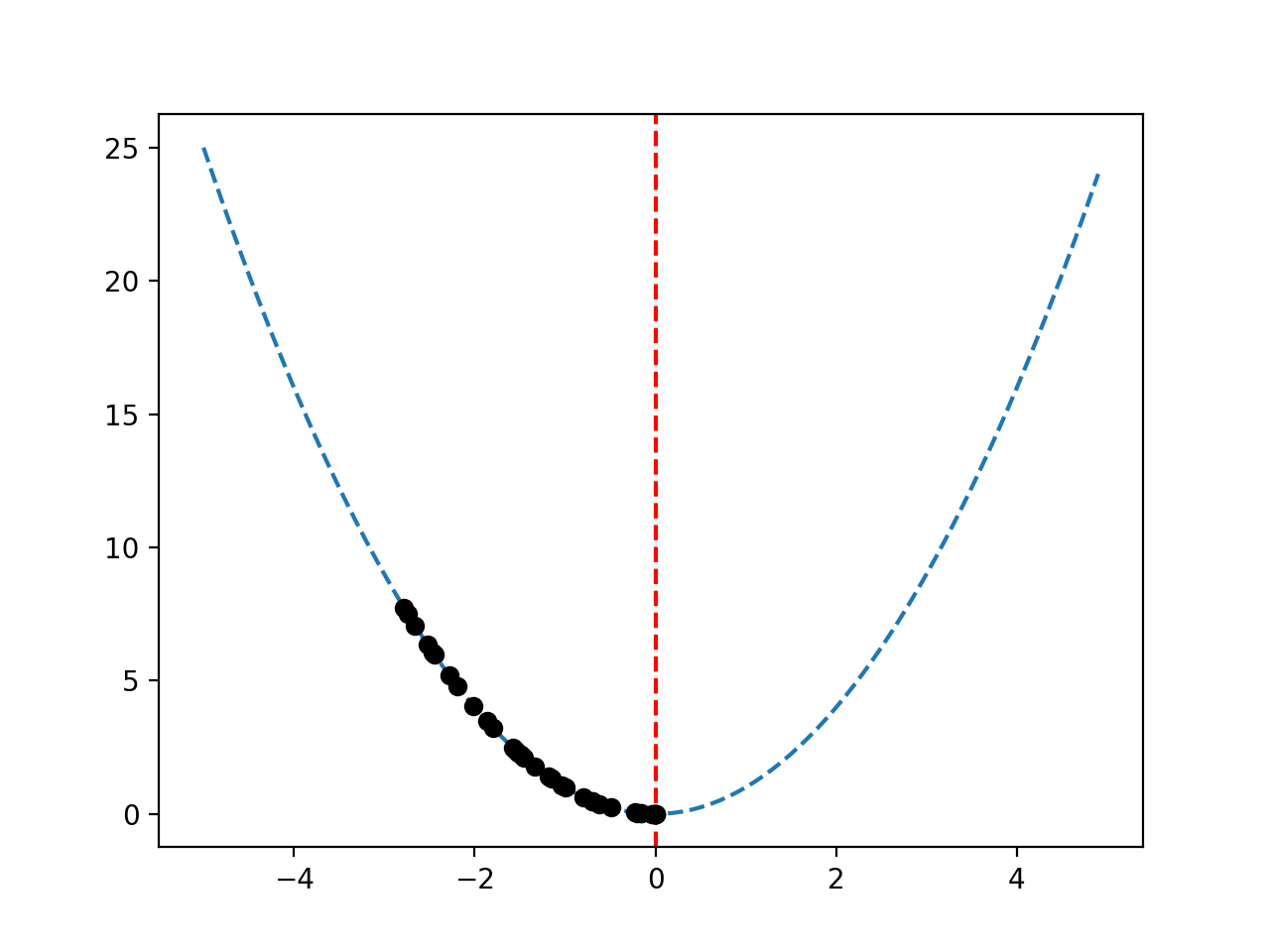
A continuación se presenta el ejemplo completo de la secuencia de soluciones mejoradas en la superficie de respuesta de la función objetivo.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 |
# Subir una colina en busca de una función objetiva unidimensional de numpy importación asarray de numpy importación arange de numpy.al azar importación randn de numpy.al azar importación rand de numpy.al azar importación semilla de matplotlib importación pyplot # Función objetiva def objetivo(x): volver x[[0]**2.0 # Algoritmo de búsqueda local de escalada de colinas def escalada(objetivo, bounds, n_iteraciones, tamaño_paso): # Generar un punto inicial solución = bounds[[:, 0] + rand(len(bounds)) * (bounds[[:, 1] – bounds[[:, 0]) # Evaluar el punto inicial solution_eval = objetivo(solución) # Corre la subida de la colina soluciones = lista() soluciones.anexar(solución) para i en rango(n_iteraciones): # dar un paso candidato = solución + randn(len(bounds)) * paso_tamaño # Evaluar el punto de candidato candidata_eval = objetivo(candidato) # comprobar si debemos mantener el nuevo punto si candidata_eval <= solution_eval: # Almacena el nuevo punto solución, solution_eval = candidato, candidato_eval # mantener el seguimiento de las soluciones soluciones.anexar(solución) # Reportar el progreso… imprimir(‘>%d f(%s) = %.5f’ % (i, solución, solution_eval)) volver [[solución, solution_eval, soluciones] # Sembrar el generador de números pseudoaleatorios semilla(5) # Definir el rango de entrada bounds = asarray([[[[–5.0, 5.0]]) # Definir las iteraciones totales n_iteraciones = 1000 # Definir el tamaño máximo del paso tamaño_paso = 0.1 # realizar la búsqueda de la escalada de la colina mejor, puntuación, soluciones = escalada(objetivo, bounds, n_iteraciones, tamaño_paso) imprimir(«¡Hecho!) imprimir(«f(%s) = %f % (mejor, puntuación)) # Rango de entrada de la muestra uniformemente en incrementos de 0.1 aportaciones = arange(bounds[[0,0], bounds[[0,1], 0.1) # Crear un gráfico de líneas de entrada vs. resultado pyplot.parcela(aportaciones, [[objetivo([[x]) para x en aportaciones], ‘–‘) # Dibujar una línea vertical en la entrada óptima pyplot.axvline(x=[[0.0], ls=‘–‘, color=«rojo) # trazar la muestra como círculos negros pyplot.parcela(soluciones, [[objetivo(x) para x en soluciones], ‘o’, color=«negro) pyplot.mostrar() |
Ejecutando el ejemplo se realiza la búsqueda de escalada de colinas y se reportan los resultados como antes.
Se crea un gráfico de la superficie de respuesta como antes, mostrando la familiar forma de tazón de la función con una línea roja vertical que marca el óptimo de la función.
La secuencia de las mejores soluciones encontradas durante la búsqueda se muestra como puntos negros que recorren la forma del cuenco hasta el óptico.

Superficie de respuesta de la función objetivo con la secuencia de las mejores soluciones trazadas como puntos negros
Más lecturas
Esta sección proporciona más recursos sobre el tema si desea profundizar en él.
Tutoriales
Libros
APIs
Artículos
Resumen
En este tutorial, usted descubrió el algoritmo de optimización de escalada de colinas para la optimización de la función
Específicamente, aprendiste:
- La escalada de colinas es un algoritmo de búsqueda local estocástico para la optimización de funciones.
- Cómo implementar el algoritmo de escalada de colinas desde cero en Python.
- Cómo aplicar el algoritmo de escalada de colinas e inspeccionar los resultados del algoritmo.
¿Tiene alguna pregunta?
Haga sus preguntas en los comentarios de abajo y haré lo posible por responder.
