La arquitectura Tree-3 y los pesos iniciales
La arquitectura Tree-3 (Fig. 1c) consta de M = 16 ramas. La primera capa de cada rama consta de K (6 o 15) filtros de tamaño (5 × 5) para cada uno de los tres canales RGB. Cada canal está convolucionado con su propio conjunto de K filtros, lo que da como resultado 3 × K filtros diferentes. Los filtros de capa convolucional son idénticos entre las ramas M. La primera capa termina con una agrupación máxima que consta de (2 × 2) cuadrados no superpuestos. La segunda capa consiste en un muestreo de árboles. Para el conjunto de datos CIFAR-10, esta capa conecta unidades ocultas de la primera capa utilizando rectángulos de tamaño no superpuestos (2 × 2 × 7), dos filas consecutivas del cuadrado de 14 × 14, sin pesos compartidos, pero con suma sobre la profundidad de los filtros K, lo que produce una salida de (16 × 3 × 7) unidades ocultas. La tercera capa conecta completamente las unidades ocultas (16 × 3 × 7) de la segunda capa con las 10 unidades de salida, que representan las 10 etiquetas diferentes. Para el conjunto de datos MNIST, la entrada es (28 × 28) y después de la convolución (5 × 5), la salida de cada filtro es (24 × 24), que termina como (12 × 12) unidades ocultas después de realizar la agrupación máxima. La capa de muestreo del árbol conecta las unidades ocultas de la primera capa utilizando rectángulos de tamaño (4 × 4 × 3) que no se superponen, sin pesos compartidos, pero con la suma sobre la profundidad de K filtros, lo que da como resultado una capa de (16 × 3 ) unidades ocultas. La tercera capa conecta completamente las unidades ocultas (16 × 3) de la segunda capa con las 10 unidades de salida, que representan las 10 etiquetas diferentes. Para el aprendizaje en línea, se usa la función de activación de ReLU, mientras que Sigmoid se usa para el aprendizaje fuera de línea, excepto para K = 15, M = 80, donde se usa la función de activación de ReLU. Todos los pesos se inicializan utilizando una distribución gaussiana con media cero y desviación estándar de acuerdo con la inicialización normal He26.
Los detalles de los tamaños de peso, entrada y salida para cada capa de la arquitectura Tree-3 se resumen a continuación.
|
Escribe |
Tamaño del peso |
Tamaño de entrada |
Tamaño de salida |
|---|---|---|---|
|
Conv2d |
(3mathrm{ x }mathrm{K x }5mathrm{ x }5) grupos = 3 | (3mathrm{ x }32mathrm{ x }32) | (3mathrm{K x }28mathrm{ x }28) |
|
MaxPool2d |
(2mathrm{ x }2) | (3mathrm{K x }28mathrm{ x }28) | (3mathrm{K x }14mathrm{ x }14) |
|
Muestreo de árboles |
(3mathrm{K x M x }14mathrm{ x }14) | (3mathrm{K x }14mathrm{ x }14) | (3mathrm{M x }7) |
|
FC |
(21matemáticas{M x }10) | (3mathrm{M x }7) | (10) |
Preprocesamiento de datos
Cada píxel de entrada de una imagen se divide por el valor máximo de un píxel, 255, y luego se multiplica por 2 y se resta por 1, de modo que su rango es [− 1, 1]. El rendimiento se mejoró mediante el uso de un aumento de datos simple derivado de las imágenes originales, como el volteo y la traducción de hasta dos píxeles para cada dirección. Para el aprendizaje fuera de línea con K = 15 y M = 80, la traducción fue de hasta cuatro píxeles para cada dirección.
Mejoramiento
La función de costo de entropía cruzada se seleccionó para la tarea de clasificación y se minimizó utilizando el algoritmo de descenso de gradiente estocástico. La precisión máxima se determinó mediante la búsqueda de los hiperparámetros, es decir, la tasa de aprendizaje, la constante de impulso y la caída del peso. La validación cruzada se confirmó utilizando varias bases de datos de validación, cada una de las cuales constaba de 10.000 ejemplos aleatorios como en el conjunto de prueba. Los resultados promediados estuvieron dentro de la desviación estándar (Std) de las tasas de éxito promedio informadas. Impulso de Nésterov27 y método de regularización L228 fueron usados.
Número de rutas: LeNet-5
El número de rutas diferentes entre un peso que emerge de la imagen de entrada a la primera capa oculta y una sola unidad de salida se calcula de la siguiente manera (Fig. 1b). Considere una unidad oculta de salida de la primera capa oculta, que pertenece a una de las unidades ocultas de salida (14 × 14) de un filtro en una rama determinada. Esta unidad oculta contribuye a un máximo de 25 operaciones convolucionales diferentes para cada filtro en la segunda capa convolucional. La salida de esta capa da como resultado 16 × 25 rutas diferentes. La agrupación máxima de la segunda capa reduce el número de rutas diferentes a 16 × 25/4 = 100. Cada una de estas rutas se divide en 120 en la tercera capa totalmente conectada y se divide nuevamente en 84 en la cuarta capa totalmente conectada. Por lo tanto, el número total de rutas es 100 × 120 × 84 = 1 008 000 rutas diferentes.
Hiperparámetros para el aprendizaje fuera de línea (Tabla 1, panel superior)
Los hiperparámetros η (tasa de aprendizaje), μ (constante de momento27) y α (regularización L228), se optimizaron para el aprendizaje fuera de línea con 200 épocas. Para LeNet-5, con un tamaño de minilote de 100, η = 0,1, μ = 0,9 y α = 1e−4. Para el Árbol-3 (K = 6 o 15, M = 16 o M = 80), usando un tamaño de lote mini de 100, η = 0,075, μ = 0,965 y α = 5e−5 y para 10 Árbol-3 (K = 15, M = 80) arquitecturas donde cada una tiene una sola salida, usando un tamaño de mini-batch de 100, η = 0.05, μ = 0.97 y α = 5e−5. El programador de tasa de aprendizaje para LeNet-5, η = 0.01, 0.005, 0.001 para epochs =[0, 100), [100, 150), [150, 200], respectivamente. Para Tree-3 (K = 6, M = 16) η = 0.075, 0.05, 0.01, 0.005, 0.001, 0.0001) para épocas =[0, 50), [50, 70), [70, 100), [100, 150), [150, 175), [175,200], respectivamente. Para Tree-3 (K = 15, M = 16) η = 0.075, 0.05, 0.01, 0.0075, 0.003 para épocas =[0, 50), [50, 70), [70, 100), [100, 150), [150,200], respectivamente. Para Tree-3 (K = 15, M = 80) y 10 Tree-3 (K = 15, M = 80), η decae por un factor de 0,6 cada 20 épocas. Para Tree-3, la constante de caída de peso cambia después de la época 50 a 1e−5. Para el conjunto de datos del MNIST, los hiperparámetros optimizados tenían un tamaño de minilote de 100, η = 0,1, μ = 0,9 y α = 5e−4. El programador de tasa de aprendizaje fue el mismo que para Tree-3 (K = 15, M = 16), en el conjunto de datos CIFAR-10.
Hiperparámetros para el aprendizaje en línea (Tabla 1, panel inferior)
El tamaño del mini lote de hiperparámetros, η (tasa de aprendizaje), μ (constante de impulso27) y α (regularización L228), se optimizaron para el aprendizaje en línea utilizando los siguientes ejemplos de tres tamaños de conjuntos de datos diferentes (50k, 25k, 12,5k). Para LeNet-5, usando tamaños de mini lotes de (100, 100, 50), η = (0.012, 0.017, 0.012), μ = (0.96, 0.96, 0.94) y α = (1e−4, 3e−3, 8e−3), respectivamente. Para Tree-3 (K = 6, M = 16), usando tamaños de mini lotes de (100, 100, 50), η = (0.02, 0.03, 0.02), μ = (0.965, 0.965, 0.965) y α = (5e−7, 5e−6, 5e−5), respectivamente.
Diez arquitecturas Tree-3
Cada arquitectura Tree-3 tiene solo una unidad de salida que representa una clase. Las diez arquitecturas tienen una capa de convolución común y se entrenan en paralelo, donde finalmente se aplica la función softmax en la salida de las diez arquitecturas diferentes.
BP podado
El gradiente de un peso que emerge de una unidad de entrada conectada a una salida a través de una ruta única (arquitectura Tree-3, Fig. 1c), con función de activación ReLU distinta de cero, está dado por (Delta left({W}^{Conv}right)=Entradacdot {W}^{Árbol}cdot {W}^{FC}cdot (Salida{-}Salida{t}_{ deseado}))de lo contrario, su valor es igual a cero.
Estadísticas
Las estadísticas de las tasas de éxito promedio y sus desviaciones estándar para simulaciones de aprendizaje en línea y fuera de línea se obtuvieron utilizando 20 muestras. Las estadísticas del porcentaje de gradientes cero y sus desviaciones estándar en la Fig. 2 se obtuvieron utilizando 10 muestras diferentes, cada una entrenada durante 200 épocas.
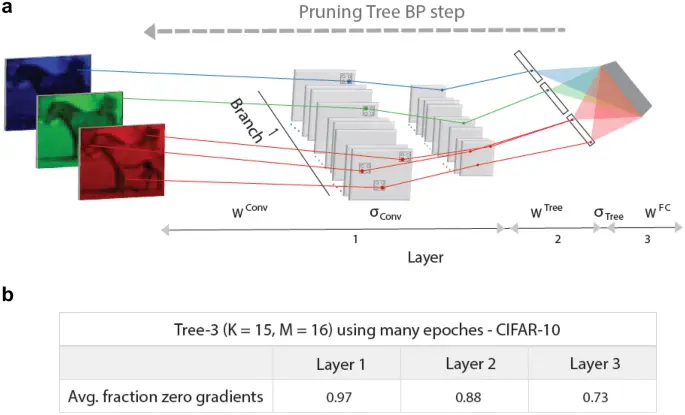
Paso de BP en la arquitectura Tree-3 de alta poda. (a) Esquema de un paso BP en la primera rama de una arquitectura Tree-3 altamente podada (Fig. 1d). Los cuadrados grises en la primera capa representan unidades ocultas convolucionales, ({sigma }_{Conversión}), y unidades ocultas de agrupación máxima que son iguales a cero, excepto varias indicadas por puntos RGB. Las unidades ocultas de salida del árbol distinto de cero, ({sigma }_{Árbol}), se indican con puntos negros. Los pesos actualizados con gradientes distintos de cero, en la primera capa, ({W}^{Conv})segunda capa, ({W}^{Árbol})y tercera capa completamente conectada, ({W}^{FC}), se indican mediante líneas RGB. (b) Fracción de gradientes cero, promediados sobre el conjunto de prueba, y sus desviaciones estándar para las capas de árbol de la arquitectura Tree-3 (K = 15, M = 16), después de muchas épocas (sección «Métodos»).
Hardware y software
Usamos Google Colab Pro y sus GPU disponibles. Usamos Pytorch para todos los procesos de programación.
