Ajuste de la curva es un tipo de optimización que encuentra un conjunto óptimo de parámetros para una función definida que se ajusta mejor a un conjunto determinado de observaciones.
A diferencia del aprendizaje supervisado, el ajuste de la curva requiere que se defina la función que asigna ejemplos de entradas a salidas.
La función de mapeo, también llamada función base, puede tener cualquier forma que se desee, incluyendo una línea recta (regresión lineal), una línea curva (regresión polinómica), y mucho más. Esto proporciona la flexibilidad y el control para definir la forma de la curva, donde se utiliza un proceso de optimización para encontrar los parámetros óptimos específicos de la función.
En este tutorial, descubrirás cómo realizar el ajuste de curvas en Python.
Después de completar este tutorial, lo sabrás:
- El ajuste de la curva consiste en encontrar los parámetros óptimos para una función que asigna ejemplos de entradas a salidas.
- La biblioteca de SciPy Python proporciona una API para ajustar una curva a un conjunto de datos.
- Cómo usar el ajuste de curvas en SciPy para ajustar un rango de diferentes curvas a un conjunto de observaciones.
Empecemos.

Curva que encaja con la pitón
Foto de Gael Varoquaux, algunos derechos reservados.
Resumen del Tutorial
Este tutorial está dividido en tres partes; son:
- Ajuste de la curva
- API de Pitón de ajuste de curva
- Ejemplo de ajuste de la curva trabajada
Ajuste de la curva
El ajuste de la curva es un problema de optimización que encuentra una línea que se ajusta mejor a una colección de observaciones.
Es más fácil pensar en el ajuste de la curva en dos dimensiones, como un gráfico.
Considere que hemos reunido ejemplos de datos del ámbito del problema con entradas y salidas.
El eje x es la variable independiente o la entrada de la función. El eje y es la variable dependiente o la salida de la función. No conocemos la forma de la función que asigna ejemplos de entradas a salidas, pero sospechamos que podemos aproximar la función con una forma de función estándar.
El ajuste de la curva consiste en definir primero la forma funcional de la función cartográfica (también llamada función de base o función objetiva), y luego buscar los parámetros de la función que den como resultado el mínimo error.
El error se calcula utilizando las observaciones del dominio y pasando las entradas a nuestra función de mapeo de candidatos y calculando la salida, y luego comparando la salida calculada con la salida observada.
Una vez ajustado, podemos usar la función de mapeo para interpolar o extrapolar nuevos puntos en el dominio. Es común ejecutar una secuencia de valores de entrada a través de la función de mapeo para calcular una secuencia de salidas, y luego crear un gráfico lineal del resultado para mostrar cómo varía la salida con la entrada y qué tan bien se ajusta la línea a los puntos observados.
La clave para el ajuste de la curva es la forma de la función de mapeo.
Una línea recta entre las entradas y las salidas puede definirse como sigue:
Donde y es la salida calculada, x es la entrada, y a y b son parámetros de la función de mapeo que se encuentran usando un algoritmo de optimización.
Se llama ecuación lineal porque es una suma ponderada de las entradas.
En un modelo de regresión lineal, estos parámetros se denominan coeficientes; en una red neuronal, se denominan pesos.
Esta ecuación puede generalizarse a cualquier número de entradas, lo que significa que la noción de ajuste de la curva no se limita a dos dimensiones (una de entrada y otra de salida), sino que podría tener muchas variables de entrada.
Por ejemplo, una función de mapeo de líneas para dos variables de entrada puede tener el siguiente aspecto:
- y = a1 * x1 + a2 * x2 + b
La ecuación no tiene que ser una línea recta.
Podemos añadir curvas en la función de mapeo añadiendo exponentes. Por ejemplo, podemos añadir una versión cuadrada de la entrada ponderada por otro parámetro:
Esto se llama regresión polinómica, y el término cuadrado significa que es un polinomio de segundo grado.
Hasta ahora, las ecuaciones lineales de este tipo pueden ser ajustadas minimizando los mínimos cuadrados y pueden ser calculadas analíticamente. Esto significa que podemos encontrar los valores óptimos de los parámetros usando un poco de álgebra lineal.
También podríamos querer añadir otras funciones matemáticas a la ecuación, como el seno, el coseno y más. Cada término se pondera con un parámetro y se añade al conjunto para dar el resultado; por ejemplo:
Añadir funciones matemáticas arbitrarias a nuestra función de mapeo generalmente significa que no podemos calcular los parámetros analíticamente, y en su lugar, necesitaremos usar un algoritmo de optimización iterativo.
Esto se llama mínimos cuadrados no lineales, ya que la función objetiva ya no es convexa (no es lineal) y no es tan fácil de resolver.
Ahora que estamos familiarizados con el ajuste de curvas, veamos cómo podríamos realizar el ajuste de curvas en Python.
API de Pitón de ajuste de curva
Podemos realizar el ajuste de la curva para nuestro conjunto de datos en Python.
La biblioteca de código abierto de SciPy proporciona la función curve_fit() para el ajuste de la curva mediante mínimos cuadrados no lineales.
La función toma los mismos datos de entrada y salida como argumentos, así como el nombre de la función de mapeo a utilizar.
La función de mapeo debe tomar ejemplos de datos de entrada y algún número de argumentos. Estos argumentos restantes serán los coeficientes o constantes de peso que se optimizarán mediante un proceso de optimización de mínimos cuadrados no lineales.
Por ejemplo, podemos tener algunas observaciones de nuestro dominio cargadas como variables de entrada x y las variables de salida y.
|
... # Cargar las variables de entrada de un archivo x_valores = ... y_valores = ... |
A continuación, necesitamos diseñar una función de mapeo para ajustar una línea a los datos e implementarla como una función de Python que toma los datos de entrada y los argumentos.
Puede ser una línea recta, en cuyo caso se vería así:
|
# Función objetiva def objetivo(x, a, b, c): volver a * x + b |
Podemos entonces llamar a la función curve_fit() para ajustar una línea recta al conjunto de datos usando nuestra función definida.
La función curve_fit() devuelve los valores óptimos para la función de mapeo, por ejemplo, los valores de los coeficientes. También devuelve una matriz de covarianza para los parámetros estimados, pero podemos ignorar eso por ahora.
|
... # Curva de ajuste popt, _ = curve_fit(objetivo, x_valores, y_valores) |
Una vez ajustado, podemos usar los parámetros óptimos y nuestra función de mapeo objetivo() para calcular la salida de cualquier entrada arbitraria.
Esto podría incluir el resultado de los ejemplos que ya hemos recogido del dominio, podría incluir nuevos valores que interpolen los valores observados, o podría incluir valores extrapolados fuera de los límites de lo observado.
|
... # Definir nuevos valores de entrada x_nuevo = ... # Desempaquetar los parámetros óptimos para la función objetivo a, b, c = popt # Usar parámetros óptimos para calcular nuevos valores y_nuevo = objetivo(x_nuevo, a, b, c) |
Ahora que estamos familiarizados con el uso de la API de ajuste de curvas, veamos un ejemplo trabajado.
Ejemplo de ajuste de la curva trabajada
Desarrollaremos una curva para ajustar algunas observaciones del mundo real de los datos económicos.
En este ejemplo, usaremos el llamado «La regresión económica de Longley«; puedes aprender más sobre ello aquí:
Descargaremos el conjunto de datos automáticamente como parte del ejemplo trabajado.
Hay siete variables de entrada y 16 filas de datos, en las que cada fila define un resumen de los detalles económicos de un año entre 1947 y 1962.
En este ejemplo, exploraremos el ajuste de una línea entre el tamaño de la población y el número de personas empleadas para cada año.
El siguiente ejemplo carga el conjunto de datos de la URL, selecciona la variable de entrada como «poblacióny la variable de salida como «empleado«…y crea una trama de dispersión.
|
# Trama «Población» vs «Empleados» de pandas importación read_csv de matplotlib importación pyplot # Cargar el conjunto de datos url = ‘https://raw.githubusercontent.com/jbrownlee/Datasets/master/longley.csv’ dataframe = read_csv(url, encabezado=Ninguno) datos = dataframe.valores # Elegir las variables de entrada y salida x, y = datos[[:, 4], datos[[:, –1] # trazar la entrada contra la salida pyplot.Dispersión(x, y) pyplot.mostrar() |
Ejecutando el ejemplo se carga el conjunto de datos, se seleccionan las variables y se crea un gráfico de dispersión.
Podemos ver que hay una relación entre las dos variables. Específicamente, que a medida que la población aumenta, el número total de empleados aumenta.
No es descabellado pensar que podemos ajustar una línea a estos datos.
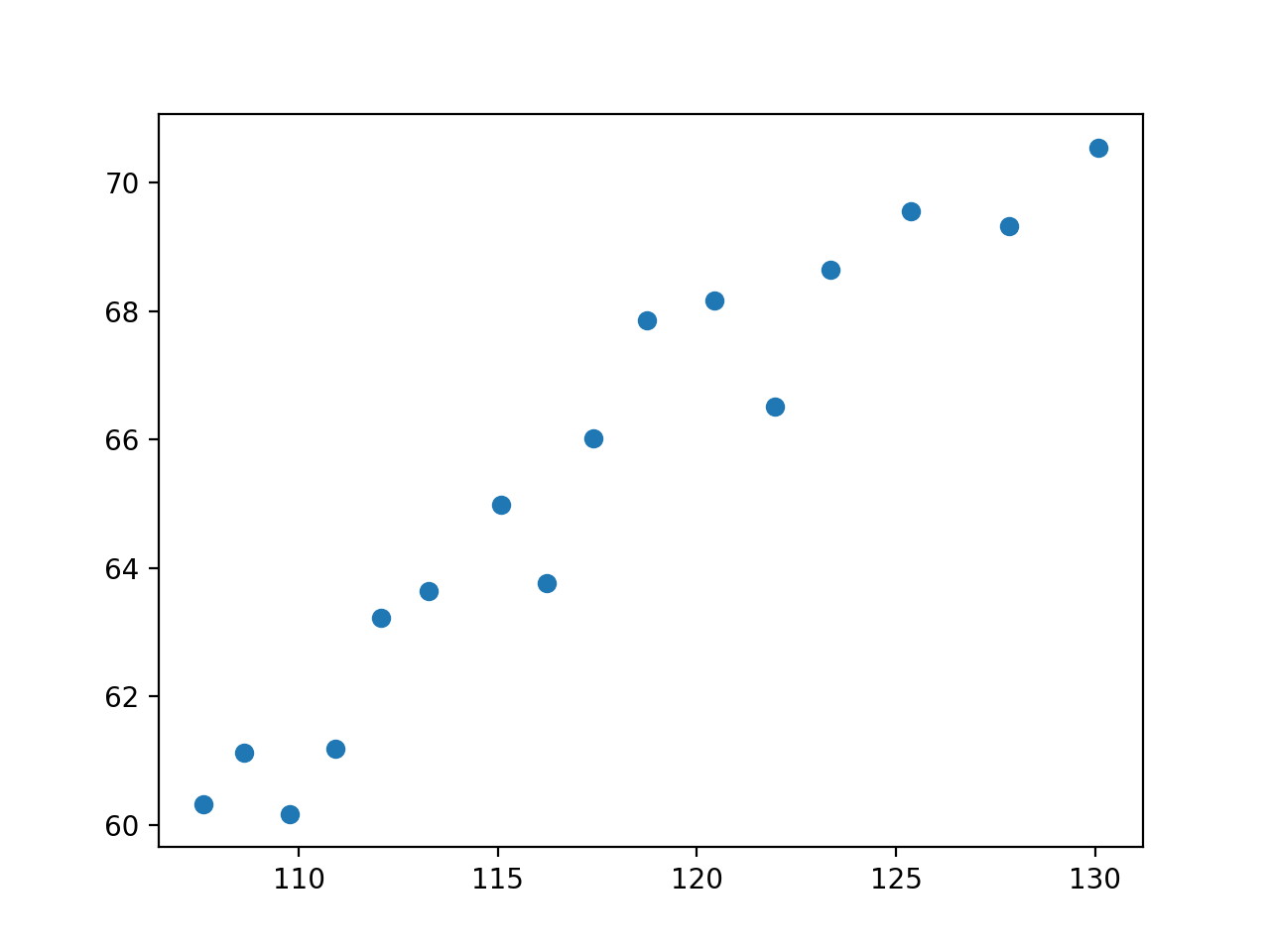
Diagrama de dispersión de la población vs. total de empleados
Primero, intentaremos ajustar una línea recta a estos datos, como sigue:
|
# Definir la verdadera función objetiva def objetivo(x, a, b): volver a * x + b |
Podemos usar el ajuste de la curva para encontrar los valores óptimos de «a«y»b» y resumir los valores que se encontraron:
|
... # Ajuste curvo popt, _ = curve_fit(objetivo, x, y) # resumir los valores de los parámetros a, b = popt imprimir(«y = %.5f * x + %.5f % (a, b)) |
Entonces podemos crear una trama de dispersión como antes.
|
... # trazar la entrada contra la salida pyplot.Dispersión(x, y) |
En la parte superior del diagrama de dispersión, podemos dibujar una línea para la función con los valores de los parámetros optimizados.
Esto implica en primer lugar definir una secuencia de valores de entrada entre los valores mínimo y máximo observados en el conjunto de datos (por ejemplo, entre unos 120 y unos 130).
|
... # Definir una secuencia de entradas entre las más pequeñas y las más grandes entradas conocidas x_line = arange(min(x), max(x), 1) |
Podemos entonces calcular el valor de salida para cada valor de entrada.
|
... # Calcular la salida para el rango y_line = objetivo(x_line, a, b) |
Entonces crea un gráfico de líneas de las entradas contra las salidas para ver una línea:
|
... # Crear un trazado de líneas para la función de mapeo pyplot.parcela(x_line, y_line, ‘–‘, color=«rojo) |
Uniendo todo esto, el siguiente ejemplo utiliza el ajuste de la curva para encontrar los parámetros de una línea recta para nuestros datos económicos.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
# ajustar una línea recta a los datos económicos de numpy importación arange de pandas importación read_csv de scipy.Optimizar importación curve_fit de matplotlib importación pyplot # Definir la verdadera función objetiva def objetivo(x, a, b): volver a * x + b # Cargar el conjunto de datos url = ‘https://raw.githubusercontent.com/jbrownlee/Datasets/master/longley.csv’ dataframe = read_csv(url, encabezado=Ninguno) datos = dataframe.valores # Elegir las variables de entrada y salida x, y = datos[[:, 4], datos[[:, –1] # Ajuste curvo popt, _ = curve_fit(objetivo, x, y) # resumir los valores de los parámetros a, b = popt imprimir(«y = %.5f * x + %.5f % (a, b)) # trazar la entrada contra la salida pyplot.Dispersión(x, y) # Definir una secuencia de entradas entre las más pequeñas y las más grandes entradas conocidas x_line = arange(min(x), max(x), 1) # Calcular la salida para el rango y_line = objetivo(x_line, a, b) # Crear un trazado de líneas para la función de mapeo pyplot.parcela(x_line, y_line, ‘–‘, color=«rojo) pyplot.mostrar() |
Ejecutando el ejemplo se realiza el ajuste de la curva y se encuentran los parámetros óptimos para nuestra función objetivo.
En primer lugar, se informa de los valores de los parámetros.
|
y = 0.48488 * x + 8.38067 |
A continuación, se crea un gráfico que muestra los datos originales y la línea que se ajustaba a los datos.
Podemos ver que es un ajuste razonablemente bueno.
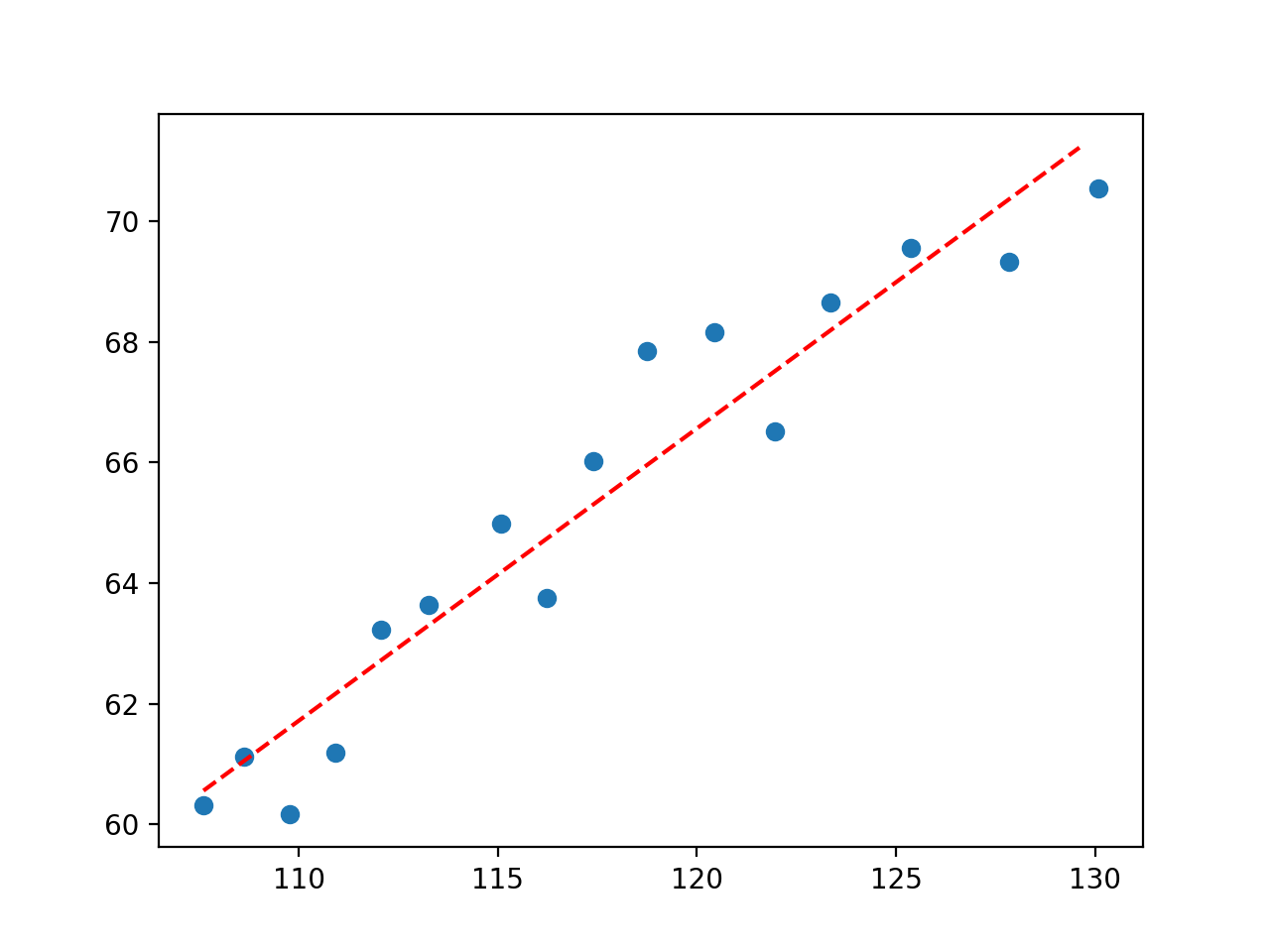
La trama de la línea recta se ajusta al conjunto de datos económicos
Hasta ahora, esto no es muy emocionante ya que podríamos lograr el mismo efecto ajustando un modelo de regresión lineal en el conjunto de datos.
Intentemos un modelo de regresión polinómica añadiendo términos cuadrados a la función objetivo.
|
# Definir la verdadera función objetiva def objetivo(x, a, b, c): volver a * x + b * x**2 + c |
A continuación se muestra el ejemplo completo.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
# ajustar un polinomio de segundo grado a los datos económicos de numpy importación arange de pandas importación read_csv de scipy.Optimizar importación curve_fit de matplotlib importación pyplot # Definir la verdadera función objetiva def objetivo(x, a, b, c): volver a * x + b * x**2 + c # Cargar el conjunto de datos url = ‘https://raw.githubusercontent.com/jbrownlee/Datasets/master/longley.csv’ dataframe = read_csv(url, encabezado=Ninguno) datos = dataframe.valores # Elegir las variables de entrada y salida x, y = datos[[:, 4], datos[[:, –1] # Ajuste curvo popt, _ = curve_fit(objetivo, x, y) # resumir los valores de los parámetros a, b, c = popt imprimir(«y = %.5f * x + %.5f * x^2 + %.5f % (a, b, c)) # trazar la entrada contra la salida pyplot.Dispersión(x, y) # Definir una secuencia de entradas entre las más pequeñas y las más grandes entradas conocidas x_line = arange(min(x), max(x), 1) # Calcular la salida para el rango y_line = objetivo(x_line, a, b, c) # Crear un trazado de líneas para la función de mapeo pyplot.parcela(x_line, y_line, ‘–‘, color=«rojo) pyplot.mostrar() |
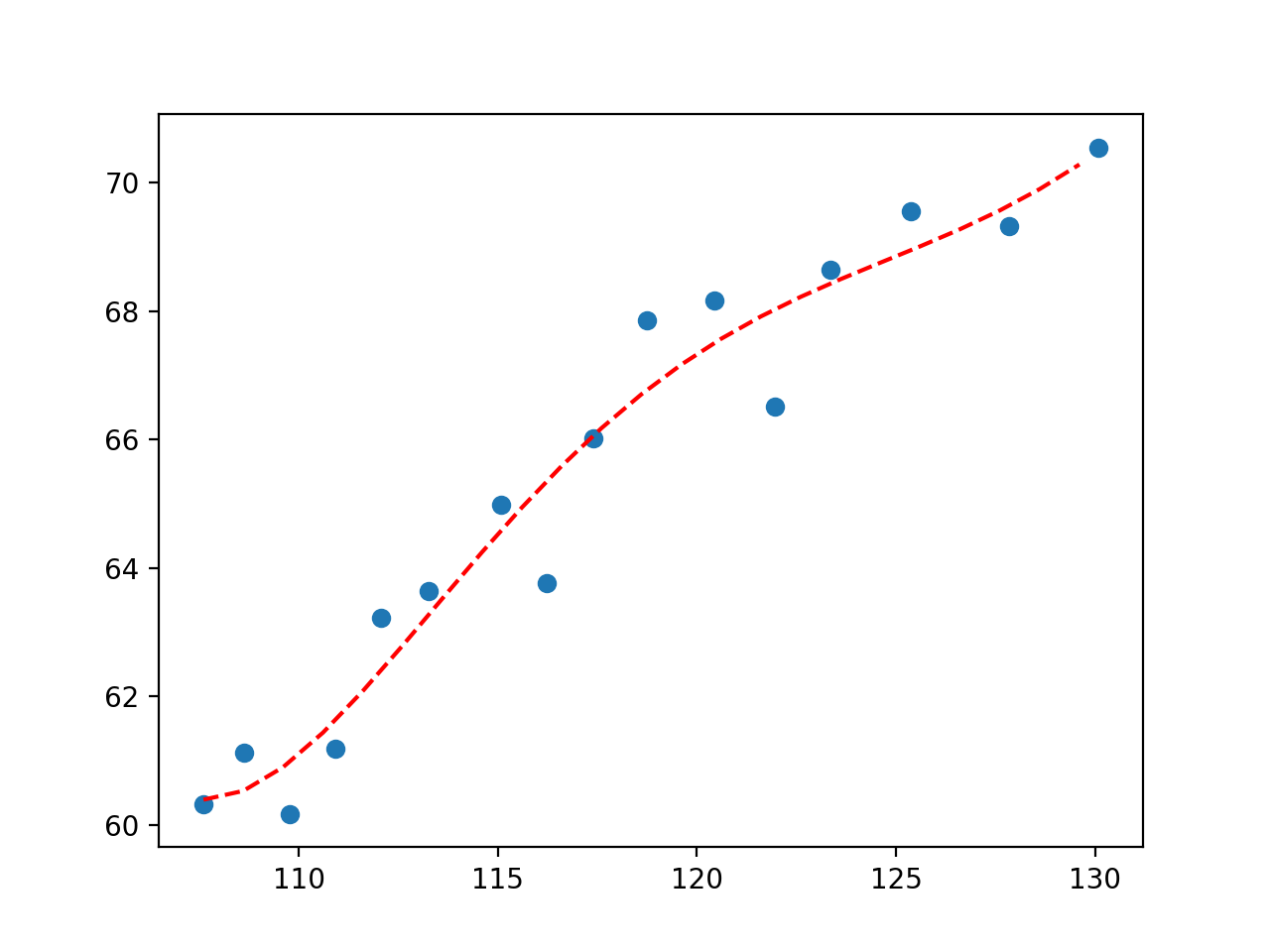
Primero se informa de los parámetros óptimos.
|
y = 3.25443 * x + -0.01170 * x^2 + -155.02783 |
A continuación, se crea una trama que muestra la línea en el contexto de los valores observados del dominio.
Podemos ver que la ecuación polinómica de segundo grado que definimos es visualmente más adecuada para los datos que la línea recta que probamos primero.

Parcela de polinomio de segundo grado para el conjunto de datos económicos
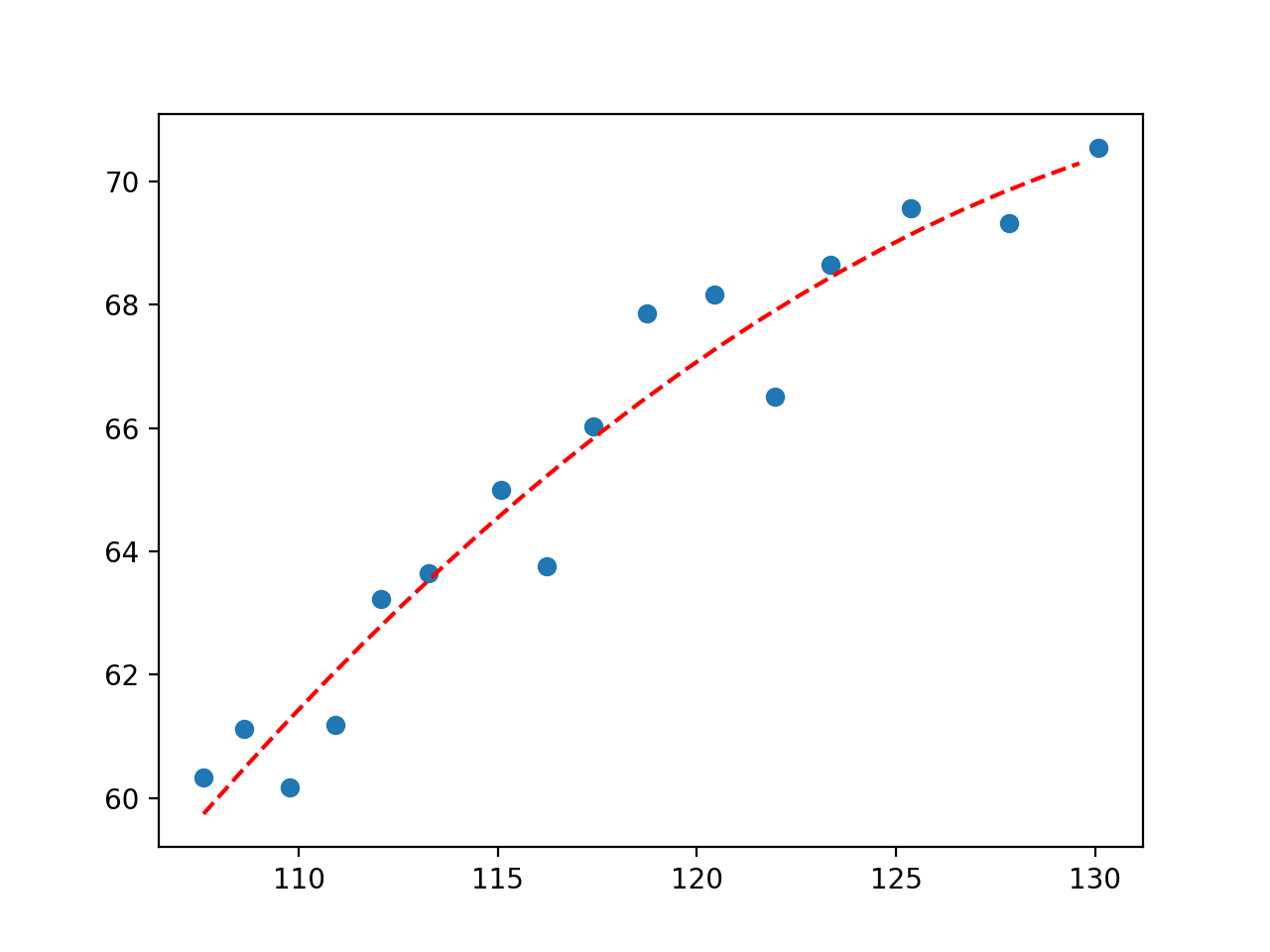
Podríamos seguir adelante y añadir más términos polinómicos a la ecuación para ajustar mejor la curva.
Por ejemplo, a continuación se presenta un ejemplo de un ajuste polinómico de quinto grado a los datos.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
# ajustar un polinomio de quinto grado a los datos económicos de numpy importación arange de pandas importación read_csv de scipy.Optimizar importación curve_fit de matplotlib importación pyplot # Definir la verdadera función objetiva def objetivo(x, a, b, c, d, e, f): volver (a * x) + (b * x**2) + (c * x**3) + (d * x**4) + (e * x**5) + f # Cargar el conjunto de datos url = ‘https://raw.githubusercontent.com/jbrownlee/Datasets/master/longley.csv’ dataframe = read_csv(url, encabezado=Ninguno) datos = dataframe.valores # Elegir las variables de entrada y salida x, y = datos[[:, 4], datos[[:, –1] # Ajuste curvo popt, _ = curve_fit(objetivo, x, y) # resumir los valores de los parámetros a, b, c, d, e, f = popt # trazar la entrada contra la salida pyplot.Dispersión(x, y) # Definir una secuencia de entradas entre las más pequeñas y las más grandes entradas conocidas x_line = arange(min(x), max(x), 1) # Calcular la salida para el rango y_line = objetivo(x_line, a, b, c, d, e, f) # Crear un trazado de líneas para la función de mapeo pyplot.parcela(x_line, y_line, ‘–‘, color=«rojo) pyplot.mostrar() |
Al ejecutar el ejemplo se ajusta la curva y se traza el resultado, capturando de nuevo un poco más de matiz en la forma en que la relación en los datos cambia con el tiempo.
Parcela de la polinomia de quinto grado que se ajusta al conjunto de datos económicos
Es importante que no nos limitemos a la regresión lineal o a la regresión polinómica. Podemos usar cualquier función de base arbitraria.
Por ejemplo, tal vez queramos una línea que se contonee para capturar el movimiento a corto plazo en la observación. Podríamos añadir una curva sinusoidal a la ecuación y encontrar los parámetros que mejor integran este elemento en la ecuación.
Por ejemplo, a continuación se enumera una función arbitraria que utiliza una onda sinusoidal y un polinomio de segundo grado:
|
# Definir la verdadera función objetiva def objetivo(x, a, b, c, d): volver a * sin(b – x) + c * x**2 + d |
El ejemplo completo de ajuste de una curva utilizando esta función de base se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
# ajustar una línea a los datos económicos de numpy importación sin de numpy importación sqrt de numpy importación arange de pandas importación read_csv de scipy.Optimizar importación curve_fit de matplotlib importación pyplot # Definir la verdadera función objetiva def objetivo(x, a, b, c, d): volver a * sin(b – x) + c * x**2 + d # Cargar el conjunto de datos url = ‘https://raw.githubusercontent.com/jbrownlee/Datasets/master/longley.csv’ dataframe = read_csv(url, encabezado=Ninguno) datos = dataframe.valores # Elegir las variables de entrada y salida x, y = datos[[:, 4], datos[[:, –1] # Ajuste curvo popt, _ = curve_fit(objetivo, x, y) # resumir los valores de los parámetros a, b, c, d = popt imprimir(popt) # trazar la entrada contra la salida pyplot.Dispersión(x, y) # Definir una secuencia de entradas entre las más pequeñas y las más grandes entradas conocidas x_line = arange(min(x), max(x), 1) # Calcular la salida para el rango y_line = objetivo(x_line, a, b, c, d) # Crear un trazado de líneas para la función de mapeo pyplot.parcela(x_line, y_line, ‘–‘, color=«rojo) pyplot.mostrar() |
Ejecutando el ejemplo se ajusta una curva y se traza el resultado.
Podemos ver que la adición de una onda sinusoidal tiene el efecto deseado mostrando un contoneo periódico con una tendencia ascendente que proporciona otra forma de capturar las relaciones en los datos.
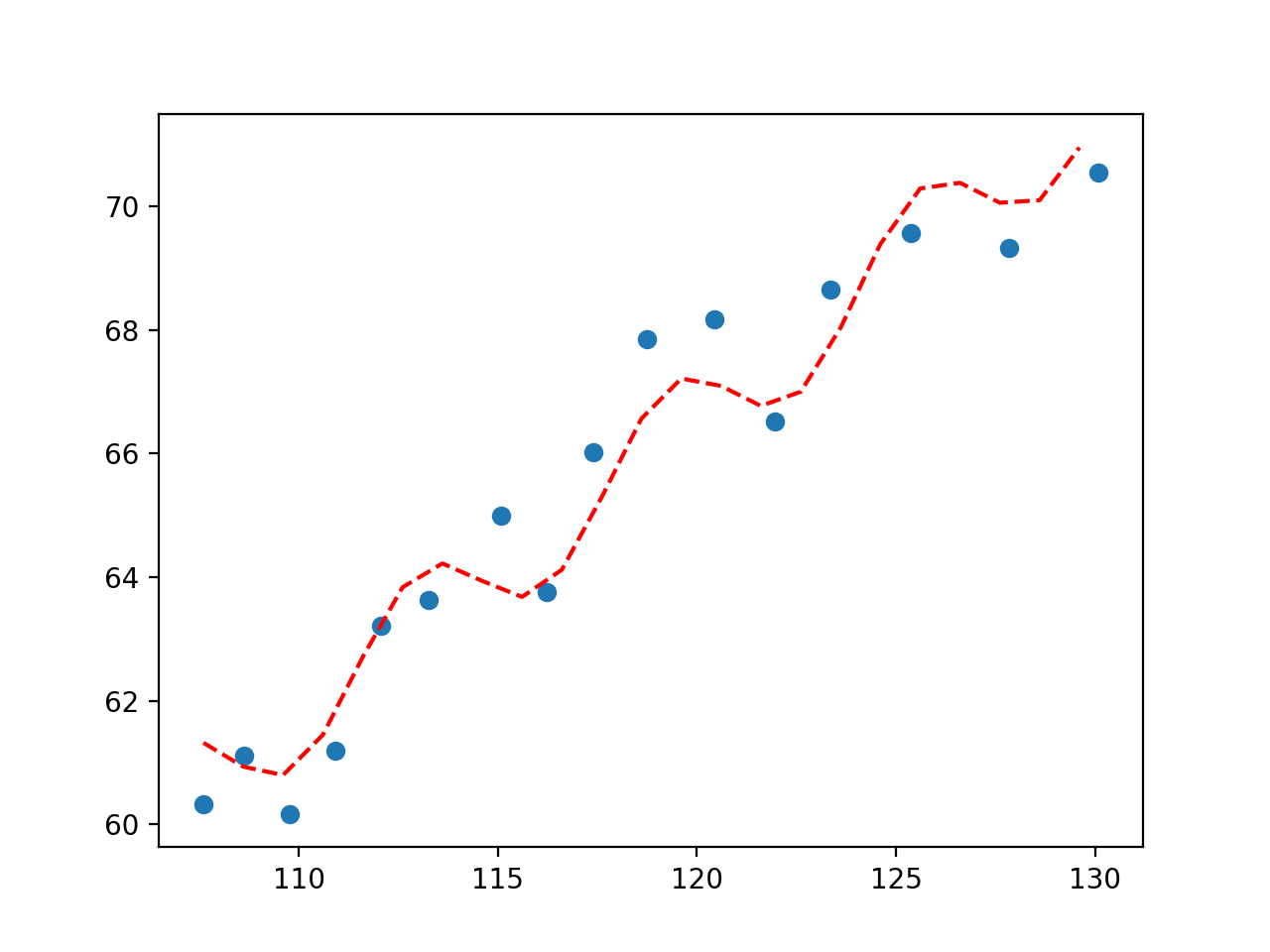
La trama de la onda sinusoidal se ajusta al conjunto de datos económicos
¿Cómo se elige el mejor ajuste?
Si quiere el mejor ajuste, modelaría el problema como un problema de aprendizaje supervisado de regresión y probaría un conjunto de algoritmos para descubrir cuál es el mejor para minimizar el error.
En este caso, el ajuste de la curva es apropiado cuando se quiere definir la función explícitamente, y luego descubrir los parámetros de su función que mejor se ajustan a una línea de los datos.
Más lecturas
Esta sección proporciona más recursos sobre el tema si desea profundizar en él.
Libros
APIs
Artículos
Resumen
En este tutorial, descubriste cómo realizar el ajuste de curvas en Python.
Específicamente, aprendiste:
- El ajuste de la curva consiste en encontrar los parámetros óptimos para una función que asigna ejemplos de entradas a salidas.
- A diferencia del aprendizaje supervisado, el ajuste de la curva requiere que se defina la función que asigna ejemplos de entradas a salidas.
- Cómo usar el ajuste de curvas en SciPy para ajustar un rango de diferentes curvas a un conjunto de observaciones.
¿Tiene alguna pregunta?
Haga sus preguntas en los comentarios de abajo y haré lo posible por responder.
