La selección de miembros del conjunto se refiere a algoritmos que optimizan la composición de un conjunto.
Esto puede implicar hacer crecer un conjunto a partir de modelos disponibles o podar miembros de un conjunto completamente definido.
El objetivo a menudo es reducir el modelo o la complejidad computacional de un conjunto con poco o ningún efecto en el rendimiento de un conjunto y, en algunos casos, encontrar una combinación de miembros del conjunto que resulte en un mejor rendimiento que usar ciegamente todos los modelos que contribuyen directamente.
En este tutorial, descubrirá cómo desarrollar algoritmos de selección de conjuntos desde cero.
Después de completar este tutorial, sabrá:
- La selección del conjunto implica elegir un subconjunto de miembros del conjunto que resulta en una menor complejidad que el uso de todos los miembros y, a veces, un mejor rendimiento.
- Cómo desarrollar y evaluar un algoritmo de poda de conjunto codicioso para la clasificación.
- Cómo desarrollar y evaluar un algoritmo para hacer crecer con avidez un conjunto desde cero.
Pon en marcha tu proyecto con mi nuevo libro Ensemble Learning Algorithms With Python, que incluye tutoriales paso a paso y el Código fuente de Python archivos para todos los ejemplos.
Empecemos.

Cultivo y poda de conjuntos en Python
Foto de FaBio C, algunos derechos reservados.
Descripción general del tutorial
Este tutorial se divide en cuatro partes; ellos son:
- Selección de miembros del conjunto
- Votación y modelos de referencia
- Ejemplo de poda de conjunto
- Ejemplo de cultivo en conjunto
Selección de miembros del conjunto
Los conjuntos de votación y apilamiento suelen combinar las predicciones de un grupo heterogéneo de tipos de modelos.
Aunque el conjunto puede tener una gran cantidad de miembros del conjunto, es difícil saber si el conjunto está utilizando la mejor combinación de miembros. Por ejemplo, en lugar de simplemente usar todos los miembros, es posible que se obtengan mejores resultados agregando un tipo de modelo más diferente o eliminando uno o más modelos.
Esto se puede abordar utilizando un conjunto de promedios ponderados y un algoritmo de optimización para encontrar una ponderación adecuada para cada miembro, lo que permite que algunos miembros tengan un peso cero, lo que los elimina efectivamente del conjunto. El problema con un conjunto de promedios ponderados es que todos los modelos siguen siendo parte del conjunto, tal vez requiriendo un conjunto de mayor complejidad de lo que se requiere para desarrollar y mantener.
Un enfoque alternativo es optimizar la composición del conjunto en sí. El enfoque general de elegir u optimizar automáticamente los miembros de los conjuntos se denomina selección de conjuntos.
Dos enfoques comunes incluyen el cultivo en conjunto y la poda en conjunto.
- Crecimiento del conjunto: Agregue miembros al conjunto hasta que no se observe ninguna mejora adicional.
- Poda de conjunto: Retire los miembros del conjunto hasta que no se observe ninguna mejora adicional.
Crecimiento de conjunto es una técnica en la que el modelo comienza sin miembros e implica agregar nuevos miembros hasta que no se observe ninguna mejora adicional. Esto podría realizarse de una manera codiciosa donde los miembros se agregan uno a la vez solo si dan como resultado una mejora en el rendimiento del modelo.
Poda de conjunto es una técnica en la que el modelo comienza con todos los miembros posibles que se están considerando y los elimina del conjunto hasta que no se observa ninguna mejora adicional. Esto podría realizarse de una manera codiciosa donde los miembros se eliminan uno a la vez y solo si su eliminación da como resultado un aumento en el rendimiento del conjunto en general.
Dado un conjunto de alumnos individuales capacitados, en lugar de combinarlos a todos, la poda por conjuntos intenta seleccionar un subconjunto de alumnos individuales para formar el conjunto.
– Página 119, Métodos de conjunto: fundamentos y algoritmos, 2012.
Una ventaja de la poda y el cultivo en conjunto es que puede resultar en un conjunto con un tamaño más pequeño (menor complejidad) y / o un conjunto con un mejor rendimiento predictivo. A veces, es deseable una pequeña caída en el rendimiento si se puede lograr en una gran caída en la complejidad del modelo y la carga de mantenimiento resultante. Alternativamente, en algunos proyectos, la habilidad predictiva es más importante que todas las demás preocupaciones, y la selección de conjuntos proporciona una estrategia más para intentar aprovechar al máximo los modelos contribuyentes.
Hay dos razones principales para reducir el tamaño del conjunto: a) Reducir la sobrecarga computacional: los conjuntos más pequeños requieren menos sobrecarga computacional yb) Mejorar la precisión: algunos miembros del conjunto pueden reducir el rendimiento predictivo del todo.
– Página 119, Clasificación de patrones utilizando métodos de conjunto, 2010.
El crecimiento del conjunto podría ser preferido por razones de eficiencia computacional en los casos en que se espera que un pequeño número de miembros del conjunto se desempeñe mejor, mientras que la poda del conjunto sería más eficiente en los casos en que se espera que un gran número de miembros del conjunto se desempeñe mejor.
El cultivo y la poda simples y codiciosos en conjunto tienen mucho en común con las técnicas de selección de características escalonadas, como las que se utilizan en la regresión (por ejemplo, la llamada regresión escalonada).
Se pueden usar técnicas más sofisticadas, como seleccionar miembros para agregar o eliminar del conjunto en función de su desempeño independiente en el conjunto de datos, o incluso mediante el uso de un procedimiento de búsqueda global que intenta encontrar una combinación de miembros del conjunto que resulte en el mejor rendimiento general.
… Uno puede realizar una búsqueda heurística en el espacio de los posibles subconjuntos de conjuntos diferentes mientras se evalúa el mérito colectivo de un subconjunto candidato.
– Página 123, Clasificación de patrones utilizando métodos de conjuntos, 2010.
Ahora que estamos familiarizados con los métodos de selección de conjuntos, exploremos cómo podemos implementar la poda de conjuntos y el crecimiento de conjuntos en scikit-learn.
¿Quiere comenzar con el aprendizaje por conjuntos?
Realice ahora mi curso intensivo gratuito de 7 días por correo electrónico (con código de muestra).
Haga clic para registrarse y obtener también una versión gratuita en formato PDF del curso.
Descarga tu minicurso GRATIS
Votación y modelos de referencia
Antes de sumergirnos en el desarrollo de conjuntos de poda y cultivo, primero establezcamos un conjunto de datos y una línea de base.
Usaremos un problema de clasificación binario sintético como base para esta investigación, definido por la función make_classification () con 5,000 ejemplos y 20 características de entrada numérica.
El siguiente ejemplo define el conjunto de datos y resume su tamaño.
|
# conjunto de datos de clasificación de prueba de sklearn.conjuntos de datos importar fabricar_clasificación # definir conjunto de datos X, y = make_classification(n_samples=5000, n_features=20, n_informativo=10, n_redundante=10, estado_aleatorio=1) # resumir el conjunto de datos impresión(X.forma, y.forma) |
Al ejecutar el ejemplo, se crea el conjunto de datos de manera repetible e informa el número de filas y características de entrada, que coinciden con nuestras expectativas.
A continuación, podemos elegir algunos modelos candidatos que proporcionarán la base para nuestro conjunto.
Usaremos cinco modelos de aprendizaje automático estándar, que incluyen regresión logística, Bayes ingenuo, árbol de decisiones, máquina de vectores de soporte y un algoritmo de vecino k-más cercano.
Primero, podemos definir una función que creará cada modelo con hiperparámetros predeterminados. Cada modelo se definirá como una tupla con un nombre y el objeto del modelo, y luego se agregará a una lista. Esta es una estructura útil tanto para enumerar los modelos con sus nombres para una evaluación independiente como para su uso posterior en un conjunto.
La get_models () La función siguiente implementa esto y devuelve la lista de modelos a considerar.
|
# obtener una lista de modelos para evaluar def get_models(): modelos = lista() modelos.adjuntar((‘lr’, Regresión logística())) modelos.adjuntar((‘knn’, KNeighborsClassifier())) modelos.adjuntar((‘árbol’, DecisionTreeClassifier())) modelos.adjuntar((‘nótese bien’, GaussianNB())) modelos.adjuntar((‘svm’, SVC(probabilidad=Cierto))) regreso modelos |
Luego, podemos definir una función que toma un solo modelo y el conjunto de datos y evalúa el rendimiento del modelo en el conjunto de datos. Evaluaremos un modelo utilizando la validación cruzada estratificada repetida de k veces con 10 pliegues y tres repeticiones, una buena práctica en el aprendizaje automático.
La evaluar_modelo () La función siguiente implementa esto y devuelve una lista de puntuaciones en todos los pliegues y repeticiones.
|
# evaluar un modelo dado mediante validación cruzada def evaluar_modelo(modelo, X, y): # definir el procedimiento de evaluación del modelo CV = Repetido Estratificado KFold(n_splits=10, n_repeats=3, estado_aleatorio=1) # evaluar el modelo puntuaciones = cross_val_score(modelo, X, y, puntuación=‘precisión’, CV=CV, n_jobs=–1) regreso puntuaciones |
Luego, podemos crear la lista de modelos y enumerarlos, informando el desempeño de cada uno en el conjunto de datos sintéticos a su vez.
Uniendo esto, el ejemplo completo se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 |
# evaluar modelos estándar en el conjunto de datos sintéticos de numpy importar significar de numpy importar std de sklearn.conjuntos de datos importar make_classification de sklearn.model_selection importar cross_val_score de sklearn.model_selection importar Repetido Estratificado KFold de sklearn.Modelo lineal importar Regresión logística de sklearn.vecinos importar KNeighborsClassifier de sklearn.árbol importar DecisionTreeClassifier de sklearn.svm importar SVC de sklearn.naive_bayes importar GaussianNB de matplotlib importar pyplot # obtener el conjunto de datos def get_dataset(): X, y = make_classification(n_samples=5000, n_features=20, n_informativo=10, n_redundante=10, estado_aleatorio=1) regreso X, y # obtener una lista de modelos para evaluar def get_models(): modelos = lista() modelos.adjuntar((‘lr’, Regresión logística())) modelos.adjuntar((‘knn’, KNeighborsClassifier())) modelos.adjuntar((‘árbol’, DecisionTreeClassifier())) modelos.adjuntar((‘nótese bien’, GaussianNB())) modelos.adjuntar((‘svm’, SVC(probabilidad=Cierto))) regreso modelos # evaluar un modelo dado mediante validación cruzada def evaluar_modelo(modelo, X, y): # definir el procedimiento de evaluación del modelo CV = Repetido Estratificado KFold(n_splits=10, n_repeats=3, estado_aleatorio=1) # evaluar el modelo puntuaciones = cross_val_score(modelo, X, y, puntuación=‘precisión’, CV=CV, n_jobs=–1) regreso puntuaciones # definir conjunto de datos X, y = get_dataset() # obtener los modelos para evaluar modelos = get_models() # evaluar los modelos y almacenar los resultados resultados, nombres = lista(), lista() por nombre, modelo en modelos: # evaluar modelo puntuaciones = evaluar_modelo(modelo, X, y) # resultados de la tienda resultados.adjuntar(puntuaciones) nombres.adjuntar(nombre) # resumir resultado impresión(‘>% s% .3f (% .3f)’ % (nombre, significar(puntuaciones), std(puntuaciones))) # trazar el rendimiento del modelo para comparar pyplot.diagrama de caja(resultados, etiquetas=nombres, mostrar significa=Cierto) pyplot.show() |
La ejecución del ejemplo evalúa cada algoritmo de aprendizaje automático independiente en el conjunto de datos de clasificación binaria sintética.
Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o procedimiento de evaluación, o las diferencias en la precisión numérica. Considere ejecutar el ejemplo varias veces y compare el resultado promedio.
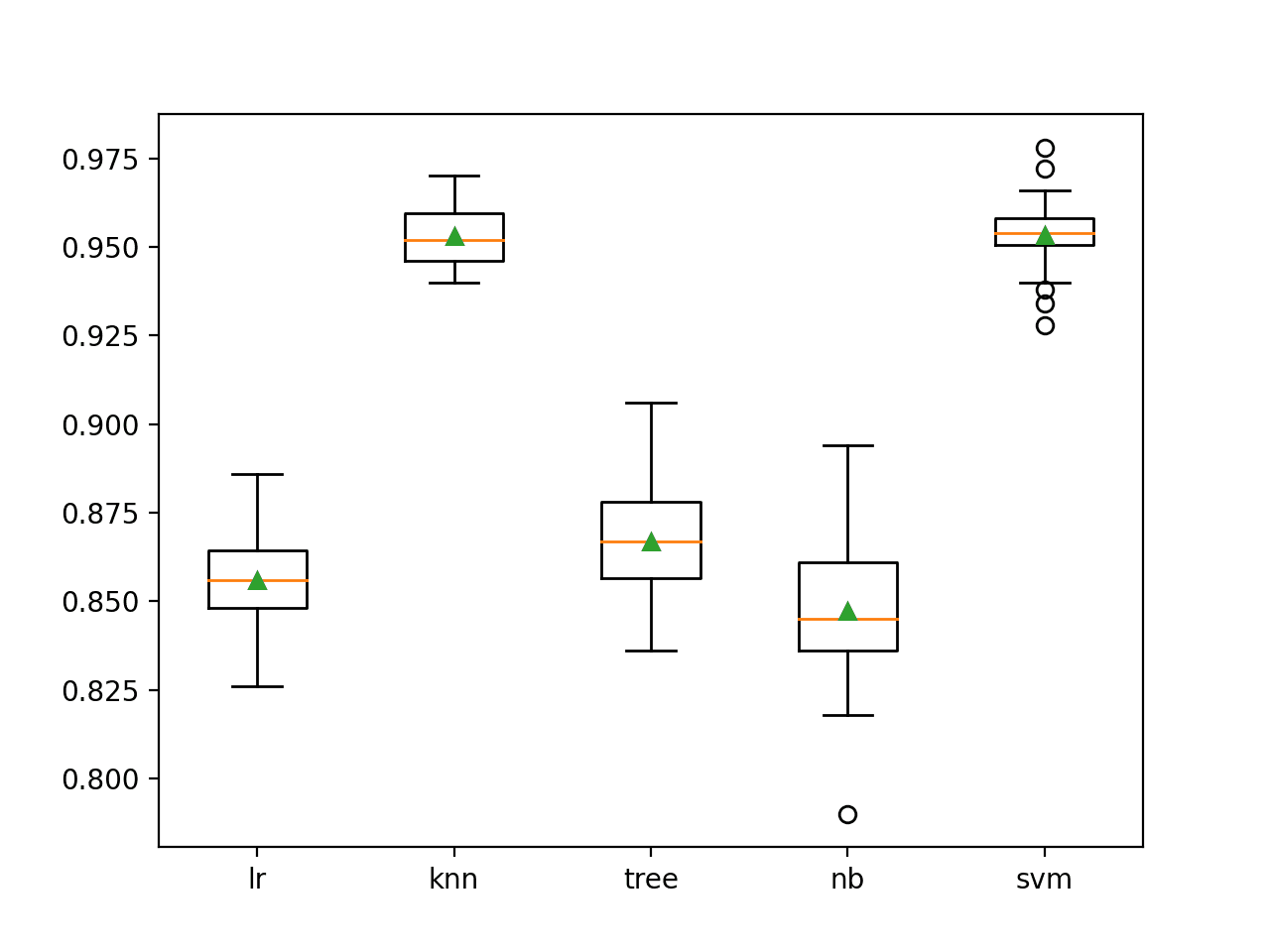
En este caso, podemos ver que los modelos KNN y SVM funcionan mejor en este conjunto de datos, logrando una precisión de clasificación media de alrededor del 95,3 por ciento.
Estos resultados proporcionan una línea de base en el rendimiento que requerimos que cualquier conjunto supere para que se considere útil en este conjunto de datos.
|
> lr 0,856 (0,014) > knn 0,953 (0,008) > árbol 0.867 (0.014) > nb 0,847 (0,021) > svm 0,953 (0,010) |
Se crea una figura que muestra diagramas de caja y bigotes de la distribución de las puntuaciones de precisión para cada algoritmo.
Podemos ver que los algoritmos KNN y SVM funcionan mucho mejor que los otros algoritmos, aunque todos los algoritmos son hábiles de diferentes maneras. Esto puede convertirlos en buenos candidatos a considerar en un conjunto.

Gráficos de caja y bigotes de precisión de clasificación para modelos autónomos de aprendizaje automático
A continuación, necesitamos establecer un conjunto de línea de base que use todos los modelos. Esto proporcionará un punto de comparación con los métodos de cultivo y poda que buscan un mejor rendimiento con un subconjunto más pequeño de modelos.
En este caso, usaremos un conjunto de votación con votación suave. Esto significa que cada modelo predecirá probabilidades y el modelo de conjunto sumará las probabilidades para elegir una predicción de salida final para cada muestra de entrada.
Esto se puede lograr usando la clase VotingClassifier donde los miembros se establecen a través de «estimadores”, Que espera una lista de modelos donde cada modelo es una tupla con un nombre y objeto de modelo configurado, tal y como definimos en la sección anterior.
A continuación, podemos establecer el tipo de votación que se realizará mediante la opción «votación«Argumento, que en este caso se establece en»suave. «
|
... # crea el conjunto conjunto = VotingClassifier(estimadores=modelos, votación=‘suave’) |
Al unir esto, el siguiente ejemplo evalúa un conjunto de votación de los cinco modelos en el conjunto de datos de clasificación binaria sintética.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
# ejemplo de un conjunto de votaciones con votación suave de los miembros del conjunto de numpy importar significar de numpy importar std de sklearn.conjuntos de datos importar make_classification de sklearn.model_selection importar cross_val_score de sklearn.model_selection importar Repetido Estratificado KFold de sklearn.Modelo lineal importar Regresión logística de sklearn.vecinos importar KNeighborsClassifier de sklearn.árbol importar DecisionTreeClassifier de sklearn.svm importar SVC de sklearn.naive_bayes importar GaussianNB de sklearn.conjunto importar VotingClassifier # obtener el conjunto de datos def get_dataset(): X, y = make_classification(n_samples=5000, n_features=20, n_informativo=10, n_redundante=10, estado_aleatorio=1) regreso X, y # obtener una lista de modelos para evaluar def get_models(): modelos = lista() modelos.adjuntar((‘lr’, Regresión logística())) modelos.adjuntar((‘knn’, KNeighborsClassifier())) modelos.adjuntar((‘árbol’, DecisionTreeClassifier())) modelos.adjuntar((‘nótese bien’, GaussianNB())) modelos.adjuntar((‘svm’, SVC(probabilidad=Cierto))) regreso modelos # definir conjunto de datos X, y = get_dataset() # obtener los modelos para evaluar modelos = get_models() # crea el conjunto conjunto = VotingClassifier(estimadores=modelos, votación=‘suave’) # definir el procedimiento de evaluación CV = Repetido Estratificado KFold(n_splits=10, n_repeats=3, estado_aleatorio=1) # evaluar el conjunto puntuaciones = cross_val_score(conjunto, X, y, puntuación=‘precisión’, CV=CV, n_jobs=–1) # resumir el resultado impresión(‘Precisión media:% .3f (% .3f)’ % (significar(puntuaciones), std(puntuaciones))) |
La ejecución del ejemplo evalúa el conjunto de votación suave de todos los modelos mediante la validación cruzada estratificada repetida de k-veces e informa la precisión media en todos los pliegues y repeticiones.
Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o procedimiento de evaluación, o las diferencias en la precisión numérica. Considere ejecutar el ejemplo varias veces y compare el resultado promedio.
En este caso, podemos ver que el conjunto de votación logró una precisión media de alrededor del 92,8 por ciento. Esto es más bajo que los modelos SVM y KNN usados solos que lograron una precisión de aproximadamente el 95,3 por ciento.
Este resultado destaca que un conjunto de votación simple de todos los modelos da como resultado un modelo con mayor complejidad y peor desempeño en este caso. Quizás podamos encontrar un subconjunto de miembros que funcione mejor que cualquier modelo individual y tenga una complejidad menor que simplemente usar todos los modelos.
|
Precisión media: 0,928 (0,012) |
A continuación, exploraremos los miembros de poda del conjunto.
Ejemplo de poda de conjunto
En esta sección, exploraremos cómo desarrollar un algoritmo de poda de conjunto codicioso desde cero.
Usaremos un algoritmo codicioso en este caso, que es sencillo de implementar. Esto implica sacar a un miembro del conjunto y evaluar la interpretación y repetir esto para cada miembro del conjunto. El miembro que, si se elimina, da como resultado la mejor mejora en el rendimiento, se elimina permanentemente del conjunto y el proceso se repite. Esto continúa hasta que no se puedan lograr más mejoras.
Se lo conoce como «avaro”Algoritmo porque busca la mejor mejora en cada paso. Es posible que la mejor combinación de miembros no esté en el camino de las mejoras codiciosas, en cuyo caso el algoritmo codicioso no la encontrará y se podría utilizar un algoritmo de optimización global en su lugar.
Primero, podemos definir una función para evaluar una lista de candidatos de modelos. Esta función tomará la lista de modelos y el conjunto de datos y construirá un conjunto de votación a partir de la lista de modelos y evaluará su desempeño utilizando la validación cruzada estratificada repetida de k-veces, devolviendo la precisión de clasificación media.
Esta función se puede utilizar para evaluar la eliminación de cada candidato del conjunto. La evaluar_ensemble () función a continuación implementa esto.
|
# evaluar una lista de modelos def evalu_ensemble(modelos, X, y): # comprobar si no hay modelos Si len(modelos) == 0: regreso 0.0 # crea el conjunto conjunto = VotingClassifier(estimadores=modelos, votación=‘suave’) # definir el procedimiento de evaluación CV = Repetido Estratificado KFold(n_splits=10, n_repeats=3, estado_aleatorio=1) # evaluar el conjunto puntuaciones = cross_val_score(conjunto, X, y, puntuación=‘precisión’, CV=CV, n_jobs=–1) # devuelve la puntuación media regreso significar(puntuaciones) |
A continuación, podemos definir una función que realice una sola ronda de poda.
Primero, se establece una línea de base en el desempeño con todos los modelos que se encuentran actualmente en el conjunto. Luego, se enumera la lista de modelos y cada uno se elimina por turno, y se evalúa el efecto de eliminar el modelo en el conjunto. Si la eliminación da como resultado una mejora en el rendimiento, se registra la nueva puntuación y el modelo específico que se eliminó.
Es importante destacar que la eliminación de prueba se realiza en una copia de la lista de modelos, no en la lista principal de modelos en sí. Esto es para asegurarnos de que solo eliminemos un miembro del conjunto de la lista una vez que sepamos que dará como resultado la mejor mejora posible de todos los miembros que podrían eliminarse en el paso actual.
La prune_round () function below implements this given the list of current models in the ensemble and dataset, and returns the improvement in score (if any) and the best model to remove to achieve that score.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 |
# perform a single round of pruning the ensemble def prune_round(models_in, X, y): # establish a baseline baseline = evaluate_ensemble(models_in, X, y) best_score, removed = baseline, None # enumerate removing each candidate and see if we can improve performance por metro in models_in: # copy the list of chosen models dup = models_in.Copiar() # remove this model dup.remove(metro) # evaluate new ensemble result = evaluate_ensemble(dup, X, y) # check for new best if result > best_score: # store the new best best_score, removed = result, metro return best_score, removed |
Next, we need to drive the pruning process.
This involves running a round of pruning until no further improvement in accuracy is achieved by calling the prune_round() function repeatedly.
If the function returns None for the model to be removed, we know that no single greedy improvement is possible and we can return the final list of models. Otherwise, the chosen model is removed from the ensemble and the process continues.
La prune_ensemble() function below implements this and returns the models to use in the final ensemble and the score that it achieved via our evaluation procedure.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 |
# prune an ensemble from scratch def prune_ensemble(models, X, y): best_score = 0.0 # prune ensemble until no further improvement while True: # remove one model to the ensemble score, removed = prune_round(models, X, y) # check for no improvement if removed is None: print(‘>no further improvement’) break # keep track of best score best_score = score # remove model from the list models.remove(removed) # report results along the way print(‘>%.3f (removed: %s)’ % (score, removed[[0])) return best_score, models |
We can tie all of this together into an example of ensemble pruning on the synthetic binary classification dataset.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 sesenta y cinco 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 |
# example of ensemble pruning for classification de numpy import mean de numpy import std de sklearn.datasets import make_classification de sklearn.model_selection import cross_val_score de sklearn.model_selection import RepeatedStratifiedKFold de sklearn.linear_model import LogisticRegression de sklearn.neighbors import KNeighborsClassifier de sklearn.tree import DecisionTreeClassifier de sklearn.svm import SVC de sklearn.naive_bayes import GaussianNB de sklearn.ensemble import VotingClassifier de matplotlib import pyplot # get the dataset def get_dataset(): X, y = make_classification(n_samples=5000, n_features=20, n_informative=10, n_redundant=10, random_state=1) return X, y # get a list of models to evaluate def get_models(): models = list() models.append((‘lr’, LogisticRegression())) models.append((‘knn’, KNeighborsClassifier())) models.append((‘tree’, DecisionTreeClassifier())) models.append((‘nb’, GaussianNB())) models.append((‘svm’, SVC(probability=True))) return models # evaluate a list of models def evaluate_ensemble(models, X, y): # check for no models if len(models) == 0: return 0.0 # create the ensemble ensemble = VotingClassifier(estimators=models, voting=‘soft’) # define the evaluation procedure cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) # evaluate the ensemble scores = cross_val_score(ensemble, X, y, scoring=‘accuracy’, cv=cv, n_jobs=–1) # return mean score return mean(scores) # perform a single round of pruning the ensemble def prune_round(models_in, X, y): # establish a baseline baseline = evaluate_ensemble(models_in, X, y) best_score, removed = baseline, None # enumerate removing each candidate and see if we can improve performance por metro in models_in: # copy the list of chosen models dup = models_in.Copiar() # remove this model dup.remove(metro) # evaluate new ensemble result = evaluate_ensemble(dup, X, y) # check for new best if result > best_score: # store the new best best_score, removed = result, metro return best_score, removed # prune an ensemble from scratch def prune_ensemble(models, X, y): best_score = 0.0 # prune ensemble until no further improvement while True: # remove one model to the ensemble score, removed = prune_round(models, X, y) # check for no improvement if removed is None: print(‘>no further improvement’) break # keep track of best score best_score = score # remove model from the list models.remove(removed) # report results along the way print(‘>%.3f (removed: %s)’ % (score, removed[[0])) return best_score, models # define dataset X, y = get_dataset() # get the models to evaluate models = get_models() # prune the ensemble score, model_list = prune_ensemble(models, X, y) names = ‘,’.join([[n por n,_ in model_list]) print(‘Models: %s’ % names) print(‘Final Mean Accuracy: %.3f’ % score) |
Running the example performs the ensemble pruning process, reporting which model was removed each round and the accuracy of the model once the model was removed.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, we can see that three rounds of pruning were performed, removing the naive Bayes, decision tree, and logistic regression algorithms, leaving only the SVM and KNN algorithms that achieved a mean classification accuracy of about 95.7 percent. This is better than the 95.3 percent achieved by SVM and KNN used in a standalone manner, and clearly better than combining all models together.
The final list of models could then be used in a new final voting ensemble model via the “estimators” argument, fit on the entire dataset and used to make a prediction on new data.
|
>0.939 (removed: nb) >0.948 (removed: tree) >0.957 (removed: lr) >no further improvement Models: knn,svm Final Mean Accuracy: 0.957 |
Now that we are familiar with developing and evaluating an ensemble pruning method, let’s look at the reverse case of growing the ensemble members.
Ensemble Growing Example
In this section, we will explore how to develop a greedy ensemble growing algorithm from scratch.
The structure of greedily growing an ensemble is much like the greedy pruning of members, although in reverse. We start with an ensemble with no models and add a single model that has the best performance. Models are then added one by one only if they result in a lift in performance over the ensemble before the model was added.
Much of the code is the same as the pruning case so we can focus on the differences.
First, we must define a function to perform one round of growing the ensemble. This involves enumerating all candidate models that could be added and evaluating the effect of adding each in turn to the ensemble. The single model that results in the biggest improvement is then returned by the function, along with its score.
La grow_round() function below implements this behavior.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 |
# perform a single round of growing the ensemble def grow_round(models_in, models_candidate, X, y): # establish a baseline baseline = evaluate_ensemble(models_in, X, y) best_score, addition = baseline, None # enumerate adding each candidate and see if we can improve performance por metro in models_candidate: # copy the list of chosen models dup = models_in.Copiar() # add the candidate dup.append(metro) # evaluate new ensemble result = evaluate_ensemble(dup, X, y) # check for new best if result > best_score: # store the new best best_score, addition = result, metro return best_score, addition |
Next, we need a function to drive the growing procedure.
This involves a loop that runs rounds of growing until no further additions can be made resulting in an improvement in model performance. For each addition that can be made, the main list of models in the ensemble is updated and the list of models currently in the ensemble is reported along with the performance.
La grow_ensemble() function implements this and returns the list of models greedily determined to result in the best performance along with the expected mean accuracy.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 |
# grow an ensemble from scratch def grow_ensemble(models, X, y): best_score, best_list = 0.0, list() # grow ensemble until no further improvement while True: # add one model to the ensemble score, addition = grow_round(best_list, models, X, y) # check for no improvement if addition is None: print(‘>no further improvement’) break # keep track of best score best_score = score # remove new model from the list of candidates models.remove(addition) # add new model to the list of models in the ensemble best_list.append(addition) # report results along the way names = ‘,’.join([[n por n,_ in best_list]) print(‘>%.3f (%s)’ % (score, names)) return best_score, best_list |
Tying this together, the complete example of greedy ensemble growing on the synthetic binary classification dataset is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 sesenta y cinco 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 |
# example of ensemble growing for classification de numpy import mean de numpy import std de sklearn.datasets import make_classification de sklearn.model_selection import cross_val_score de sklearn.model_selection import RepeatedStratifiedKFold de sklearn.linear_model import LogisticRegression de sklearn.neighbors import KNeighborsClassifier de sklearn.tree import DecisionTreeClassifier de sklearn.svm import SVC de sklearn.naive_bayes import GaussianNB de sklearn.ensemble import VotingClassifier de matplotlib import pyplot # get the dataset def get_dataset(): X, y = make_classification(n_samples=5000, n_features=20, n_informative=10, n_redundant=10, random_state=1) return X, y # get a list of models to evaluate def get_models(): models = list() models.append((‘lr’, LogisticRegression())) models.append((‘knn’, KNeighborsClassifier())) models.append((‘tree’, DecisionTreeClassifier())) models.append((‘nb’, GaussianNB())) models.append((‘svm’, SVC(probability=True))) return models # evaluate a list of models def evaluate_ensemble(models, X, y): # check for no models if len(models) == 0: return 0.0 # create the ensemble ensemble = VotingClassifier(estimators=models, voting=‘soft’) # define the evaluation procedure cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) # evaluate the ensemble scores = cross_val_score(ensemble, X, y, scoring=‘accuracy’, cv=cv, n_jobs=–1) # return mean score return mean(scores) # perform a single round of growing the ensemble def grow_round(models_in, models_candidate, X, y): # establish a baseline baseline = evaluate_ensemble(models_in, X, y) best_score, addition = baseline, None # enumerate adding each candidate and see if we can improve performance por metro in models_candidate: # copy the list of chosen models dup = models_in.Copiar() # add the candidate dup.append(metro) # evaluate new ensemble result = evaluate_ensemble(dup, X, y) # check for new best if result > best_score: # store the new best best_score, addition = result, metro return best_score, addition # grow an ensemble from scratch def grow_ensemble(models, X, y): best_score, best_list = 0.0, list() # grow ensemble until no further improvement while True: # add one model to the ensemble score, addition = grow_round(best_list, models, X, y) # check for no improvement if addition is None: print(‘>no further improvement’) break # keep track of best score best_score = score # remove new model from the list of candidates models.remove(addition) # add new model to the list of models in the ensemble best_list.append(addition) # report results along the way names = ‘,’.join([[n por n,_ in best_list]) print(‘>%.3f (%s)’ % (score, names)) return best_score, best_list # define dataset X, y = get_dataset() # get the models to evaluate models = get_models() # grow the ensemble score, model_list = grow_ensemble(models, X, y) names = ‘,’.join([[n por n,_ in model_list]) print(‘Models: %s’ % names) print(‘Final Mean Accuracy: %.3f’ % score) |
Running the example incrementally adds one model at a time to the ensemble and reports the mean classification accuracy of the ensemble of the models.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, we can see that ensemble growing found the same solution as greedy ensemble pruning where an ensemble of SVM and KNN achieved a mean classification accuracy of about 95.6 percent, an improvement over any single standalone model and over combining all models.
|
>0.953 (svm) >0.956 (svm,knn) >no further improvement Models: svm,knn Final Mean Accuracy: 0.956 |
Further Reading
This section provides more resources on the topic if you are looking to go deeper.
Tutorials
Books
APIs
Summary
In this tutorial, you discovered how to develop ensemble selection algorithms from scratch.
Specifically, you learned:
- Ensemble selection involves choosing a subset of ensemble members that results in lower complexity than using all members and sometimes better performance.
- How to develop and evaluate a greedy ensemble pruning algorithm for classification.
- How to develop and evaluate an algorithm for greedily growing an ensemble from scratch.
Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.

