
los Optimización de Nelder-Mead El algoritmo es un enfoque ampliamente utilizado para funciones objetivas no diferenciables.
Como tal, generalmente se lo conoce como un algoritmo de búsqueda de patrones y se usa como un procedimiento de búsqueda local o global, desafiando los problemas de optimización de funciones no lineales y potencialmente ruidosos y multimodales.
En este tutorial, descubrirá el algoritmo de optimización de Nelder-Mead.
Después de completar este tutorial, sabrá:
- El algoritmo de optimización de Nelder-Mead es un tipo de búsqueda de patrones que no utiliza gradientes de función.
- Cómo aplicar el algoritmo de Nelder-Mead para la optimización de funciones en Python.
- Cómo interpretar los resultados del algoritmo Nelder-Mead en funciones objetivas ruidosas y multimodales.
Empecemos.

Cómo utilizar la optimización de Nelder-Mead en Python
Foto de Don Graham, algunos derechos reservados.
Descripción general del tutorial
Este tutorial se divide en tres partes; son:
- Algoritmo de Nelder-Mead
- Ejemplo de Nelder-Mead en Python
- Nelder-Mead sobre funciones desafiantes
- Problema de optimización ruidoso
- Problema de optimización multimodal
Algoritmo de Nelder-Mead
Nelder-Mead es un algoritmo de optimización que lleva el nombre de los desarrolladores de la técnica, John Nelder y Roger Mead.
El algoritmo fue descrito en su artículo de 1965 titulado «Un método simplex para la minimización de funciones» y se ha convertido en una técnica estándar y ampliamente utilizada para la optimización de funciones.
Es apropiado para funciones unidimensionales o multidimensionales con entradas numéricas.
Nelder-Mead es un algoritmo de optimización de búsqueda de patrones, lo que significa que requiere o usa información de gradiente de función y es apropiado para problemas de optimización donde el gradiente de la función es desconocido o no se puede calcular razonablemente.
A menudo se utiliza para problemas de optimización de funciones no lineales multidimensionales, aunque puede atascarse en óptimos locales.
El rendimiento práctico del algoritmo de Nelder-Mead suele ser razonable, aunque se ha observado que se produce un estancamiento en puntos no óptimos. El reinicio se puede utilizar cuando se detecta un estancamiento.
– Página 239, Optimización numérica, 2006.
Se debe proporcionar un punto de partida al algoritmo, que puede ser el punto final de otro algoritmo de optimización global o un punto aleatorio extraído del dominio.
Dado que el algoritmo puede atascarse, puede beneficiarse de varios reinicios con diferentes puntos de partida.
El método simplex de Nelder-Mead utiliza un simplex para atravesar el espacio en busca de un mínimo.
– Página 105, Algoritmos de optimización, 2019.
El algoritmo funciona usando una estructura de forma (llamada simplex) compuesta de norte + 1 puntos (vértices), donde norte es el número de dimensiones de entrada a la función.
Por ejemplo, en un problema bidimensional que se puede trazar como una superficie, la estructura de la forma estaría compuesta por tres puntos representados como un triángulo.
El método Nelder-Mead utiliza una serie de reglas que dictan cómo se actualiza el símplex en función de las evaluaciones de la función objetivo en sus vértices.
– Página 106, Algoritmos de optimización, 2019.
Los puntos de la estructura de la forma se evalúan y se utilizan reglas simples para decidir cómo mover los puntos de la forma en función de su evaluación relativa. Esto incluye operaciones como «reflexión, «»expansión, «»contracción, «Y»contracción”De la forma simplex en la superficie de la función objetivo.
En una sola iteración del algoritmo de Nelder-Mead, buscamos eliminar el vértice con el peor valor de función y reemplazarlo con otro punto con un mejor valor. El nuevo punto se obtiene reflejando, expandiendo o contrayendo el símplex a lo largo de la línea que une el peor vértice con el centroide de los vértices restantes. Si no podemos encontrar un punto mejor de esta manera, retenemos solo el vértice con el mejor valor de función y encogemos el simplex moviendo todos los demás vértices hacia este valor.
– Página 238, Optimización numérica, 2006.
La búsqueda se detiene cuando los puntos convergen en un óptimo, cuando se observa una diferencia mínima entre evaluaciones o cuando se realiza un número máximo de evaluaciones de funciones.
Ahora que tenemos una idea de alto nivel de cómo funciona el algoritmo, veamos cómo podríamos usarlo en la práctica.
Ejemplo de Nelder-Mead en Python
El algoritmo de optimización Nelder-Mead se puede utilizar en Python a través de la función minimizar ().
Esta función requiere que el «método«Argumento se establece en»nelder-mead”Para utilizar el algoritmo de Nelder-Mead. Se necesita la función objetivo a minimizar y un punto inicial para la búsqueda.
|
... # realizar la búsqueda resultado = minimizar(objetivo, pt, método=‘nelder-mead’) |
El resultado es un objeto OptimizeResult que contiene información sobre el resultado de la optimización accesible mediante claves.
Por ejemplo, el «éxito«Booleano indica si la búsqueda se completó correctamente o no, el»mensaje«Proporciona un mensaje legible por humanos sobre el éxito o el fracaso de la búsqueda, y el»nfevLa tecla ”indica el número de evaluaciones de funciones que se realizaron.
Es importante destacar que el «XLa tecla ”especifica los valores de entrada que indican los óptimos encontrados por la búsqueda, si tiene éxito.
|
... # resumir el resultado impresión(‘Estado:% s’ % resultado[[‘mensaje’]) impresión(‘Total de evaluaciones:% d’ % resultado[[‘nfev’]) impresión(‘Solución:% s’ % resultado[[‘X’]) |
Podemos demostrar el algoritmo de optimización de Nelder-Mead en una función con buen comportamiento para demostrar que puede encontrar los óptimos de forma rápida y eficiente sin utilizar información derivada de la función.
En este caso, usaremos la función x ^ 2 en dos dimensiones, definida en el rango de -5.0 a 5.0 con el óptimo conocido en [0.0, 0.0].
Podemos definir el objetivo() función a continuación.
|
# función objetiva def objetivo(X): regreso X[[0]**2.0 + X[[1]**2.0 |
Usaremos un punto aleatorio en el dominio definido como punto de partida para la búsqueda.
|
... # definir rango para entrada r_min, r_max = –5,0, 5,0 # definir el punto de partida como una muestra aleatoria del dominio pt = r_min + rand(2) * (r_max – r_min) |
Entonces se puede realizar la búsqueda. Usamos el número máximo predeterminado de evaluaciones de funciones establecido a través del «maxiter”Y establecido en N * 200, donde N es el número de variables de entrada, que es dos en este caso, p. Ej. 400 evaluaciones.
|
... # realizar la búsqueda resultado = minimizar(objetivo, pt, método=‘nelder-mead’) |
Una vez finalizada la búsqueda, informaremos las evaluaciones de funciones totales utilizadas para encontrar los óptimos y el mensaje de éxito de la búsqueda, que esperamos sean positivos en este caso.
|
... # resumir el resultado impresión(‘Estado:% s’ % resultado[[‘mensaje’]) impresión(‘Total de evaluaciones:% d’ % resultado[[‘nfev’]) |
Finalmente, recuperaremos los valores de entrada para los óptimos localizados, los evaluaremos usando la función objetivo y reportaremos ambos de una manera legible por humanos.
|
... # evaluar la solución solución = resultado[[‘X’] evaluación = objetivo(solución) impresión(‘Solución: f (% s) =% .5f’ % (solución, evaluación)) |
Uniendo esto, el ejemplo completo del uso del algoritmo de optimización de Nelder-Mead en una función objetiva convexa simple se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 |
# optimización nelder-mead de una función convexa desde scipy.optimizar importar minimizar desde numpy.aleatorio importar rand # función objetiva def objetivo(X): regreso X[[0]**2.0 + X[[1]**2.0 # definir rango para entrada r_min, r_max = –5,0, 5,0 # definir el punto de partida como una muestra aleatoria del dominio pt = r_min + rand(2) * (r_max – r_min) # realizar la búsqueda resultado = minimizar(objetivo, pt, método=‘nelder-mead’) # resumir el resultado impresión(‘Estado:% s’ % resultado[[‘mensaje’]) impresión(‘Total de evaluaciones:% d’ % resultado[[‘nfev’]) # evaluar la solución solución = resultado[[‘X’] evaluación = objetivo(solución) impresión(‘Solución: f (% s) =% .5f’ % (solución, evaluación)) |
La ejecución del ejemplo ejecuta la optimización y luego informa los resultados.
Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o procedimiento de evaluación, o las diferencias en la precisión numérica. Considere ejecutar el ejemplo varias veces y compare el resultado promedio.
En este caso, podemos ver que la búsqueda fue exitosa, como esperábamos, y se completó después de 88 evaluaciones de funciones.
Podemos ver que el optima se ubicó con entradas muy cercanas a [0,0], que evalúa el valor objetivo mínimo de 0.0.
|
Estado: la optimización finalizó correctamente. Total de valoraciones: 88 Solución: f ([ 2.25680716e-05 -3.87021351e-05]) = 0,00000 |
Ahora que hemos visto cómo utilizar el algoritmo de optimización de Nelder-Mead con éxito, veamos algunos ejemplos en los que no funciona tan bien.
Nelder-Mead sobre funciones desafiantes
El algoritmo de optimización de Nelder-Mead funciona bien para una gama de funciones objetivas desafiantes no lineales y no diferenciables.
Sin embargo, puede atascarse en problemas de optimización multimodal y problemas ruidosos.
Para hacer esto concreto, veamos un ejemplo de cada uno.
Problema de optimización ruidoso
Una función objetiva ruidosa es una función que da diferentes respuestas cada vez que se evalúa la misma entrada.
Podemos hacer que una función objetivo sea artificialmente ruidosa agregando pequeños números aleatorios gaussianos a las entradas antes de su evaluación.
Por ejemplo, podemos definir una versión unidimensional de la función x ^ 2 y usar la función randn () para agregar pequeños números aleatorios gaussianos a la entrada con una media de 0.0 y una desviación estándar de 0.3.
|
# función objetiva def objetivo(X): regreso (X + randn(len(X))*0,3)**2.0 |
El ruido hará que la función sea difícil de optimizar para el algoritmo y es muy probable que no ubique el óptimo en x = 0.0.
El ejemplo completo del uso de Nelder-Mead para optimizar la función de objetivo ruidoso se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 |
# optimización nelder-mead de función convexa unidimensional ruidosa desde scipy.optimizar importar minimizar desde numpy.aleatorio importar rand desde numpy.aleatorio importar randn # función objetiva def objetivo(X): regreso (X + randn(len(X))*0,3)**2.0 # definir rango para entrada r_min, r_max = –5,0, 5,0 # definir el punto de partida como una muestra aleatoria del dominio pt = r_min + rand(1) * (r_max – r_min) # realizar la búsqueda resultado = minimizar(objetivo, pt, método=‘nelder-mead’) # resumir el resultado impresión(‘Estado:% s’ % resultado[[‘mensaje’]) impresión(‘Total de evaluaciones:% d’ % resultado[[‘nfev’]) # evaluar la solución solución = resultado[[‘X’] evaluación = objetivo(solución) impresión(‘Solución: f (% s) =% .5f’ % (solución, evaluación)) |
La ejecución del ejemplo ejecuta la optimización y luego informa los resultados.
Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o procedimiento de evaluación, o las diferencias en la precisión numérica. Considere ejecutar el ejemplo varias veces y compare el resultado promedio.
En este caso, el algoritmo no converge y en su lugar utiliza el número máximo de evaluaciones de funciones, que es 200.
|
Estado: se ha superado el número máximo de evaluaciones de funciones. Total de evaluaciones: 200 Solución: f ([-0.6918238]) = 0,79431 |
El algoritmo puede converger en algunas ejecuciones del código, pero llegará en un punto alejado del óptimo.
Problema de optimización multimodal
Muchas funciones objetivas no lineales pueden tener múltiples óptimos, denominados problemas multimodales.
El problema puede estar estructurado de manera que tenga múltiples óptimos globales que tengan una evaluación de función equivalente, o un único óptimo global y múltiples óptimos locales donde algoritmos como el Nelder-Mead pueden atascarse en busca de los óptimos locales.
La función Ackley es un ejemplo de esto último. Es una función objetivo bidimensional que tiene un óptimo global en [0,0] pero tiene muchos óptimos locales.
El siguiente ejemplo implementa el Ackley y crea un gráfico tridimensional que muestra los óptimos globales y múltiples óptimos locales.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
# función multimodal ackley desde numpy importar arange desde numpy importar Exp desde numpy importar sqrt desde numpy importar porque desde numpy importar mi desde numpy importar Pi desde numpy importar rejilla desde matplotlib importar pyplot desde mpl_toolkits.mplot3d importar Ejes3D # función objetiva def objetivo(X, y): regreso –20,0 * Exp(–0,2 * sqrt(0,5 * (X**2 + y **2))) – Exp(0,5 * (porque(2 * Pi * X) + porque(2 * Pi * y))) + mi + 20 # definir rango para entrada r_min, r_max = –5,0, 5,0 # rango de entrada de muestra uniformemente en incrementos de 0.1 xaxis = arange(r_min, r_max, 0,1) yaxis = arange(r_min, r_max, 0,1) # crea una malla desde el eje X, y = rejilla(xaxis, yaxis) # calcular objetivos resultados = objetivo(X, y) # crea un gráfico de superficie con el esquema de color jet figura = pyplot.figura() eje = figura.gca(proyección=‘3d’) eje.plot_surface(X, y, resultados, cmap=‘chorro’) # mostrar la trama pyplot.show() |
La ejecución del ejemplo crea el gráfico de superficie de la función Ackley que muestra la gran cantidad de óptimos locales.
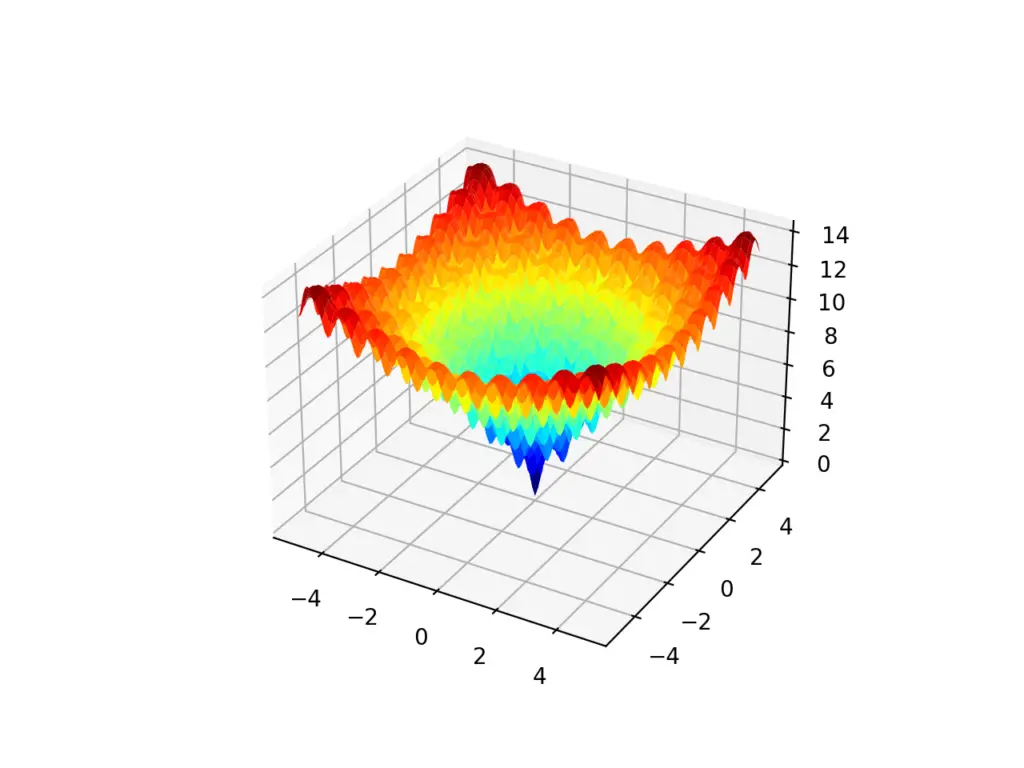
Gráfico de superficie 3D de la función multimodal de Ackley
Es de esperar que la función Nelder-Mead se atasque en uno de los óptimos locales mientras buscamos los óptimos globales.
Inicialmente, cuando el simplex es grande, el algoritmo puede saltar sobre muchos óptimos locales, pero a medida que se contrae, se atasca.
Podemos explorar esto con el siguiente ejemplo que demuestra el algoritmo de Nelder-Mead en la función Ackley.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 |
# nelder-mead para la optimización de funciones multimodales desde scipy.optimizar importar minimizar desde numpy.aleatorio importar rand desde numpy importar Exp desde numpy importar sqrt desde numpy importar porque desde numpy importar mi desde numpy importar Pi # función objetiva def objetivo(v): X, y = v regreso –20,0 * Exp(–0,2 * sqrt(0,5 * (X**2 + y **2))) – Exp(0,5 * (porque(2 * Pi * X) + porque(2 * Pi * y))) + mi + 20 # definir rango para entrada r_min, r_max = –5,0, 5,0 # definir el punto de partida como una muestra aleatoria del dominio pt = r_min + rand(2) * (r_max – r_min) # realizar la búsqueda resultado = minimizar(objetivo, pt, método=‘nelder-mead’) # resumir el resultado impresión(‘Estado:% s’ % resultado[[‘mensaje’]) impresión(‘Total de evaluaciones:% d’ % resultado[[‘nfev’]) # evaluar la solución solución = resultado[[‘X’] evaluación = objetivo(solución) impresión(‘Solución: f (% s) =% .5f’ % (solución, evaluación)) |
La ejecución del ejemplo ejecuta la optimización y luego informa los resultados.
Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o procedimiento de evaluación, o las diferencias en la precisión numérica. Considere ejecutar el ejemplo varias veces y compare el resultado promedio.
En este caso, podemos ver que la búsqueda se completó con éxito pero no localizó los óptimos globales. Se atascó y encontró un óptimo local.
Cada vez que ejecutamos el ejemplo, encontraremos un óptimo local diferente dado el punto de partida aleatorio diferente para la búsqueda.
|
Estado: la optimización finalizó correctamente. Total de valoraciones: 62 Solución: f ([-4.9831427 -3.98656015]) = 11,90126 |
Otras lecturas
Esta sección proporciona más recursos sobre el tema si está buscando profundizar.
Documentos
Libros
API
Artículos
Resumen
En este tutorial, descubrió el algoritmo de optimización de Nelder-Mead.
Específicamente, aprendiste:
- El algoritmo de optimización de Nelder-Mead es un tipo de búsqueda de patrones que no utiliza gradientes de función.
- Cómo aplicar el algoritmo de Nelder-Mead para la optimización de funciones en Python.
- Cómo interpretar los resultados del algoritmo de Nelder-Mead en funciones objetivas ruidosas y multimodales.
¿Tiene usted alguna pregunta?
Haga sus preguntas en los comentarios a continuación y haré todo lo posible para responder.
