El aprendizaje de refuerzo profundo ha hecho progresos significativos en los últimos años, con historias de éxito en el control robótico, el juego y los problemas de la ciencia. Si bien los métodos de RL presentan un paradigma general en el que un agente aprende de su propia interacción con un entorno, este requisito de recopilación «activa» de datos es también un obstáculo importante en la aplicación de los métodos de RL a los problemas del mundo real, ya que la recopilación activa de datos suele ser costosa y potencialmente insegura. Una alternativa «impulsado por datos» paradigma de RL, llamado RL fuera de línea (o lote RL) ha recuperado recientemente su popularidad como un camino viable hacia una efectiva LR en el mundo real. Como se muestra en la figura siguiente, la LR fuera de línea requiere el aprendizaje de habilidades únicamente a partir de conjuntos de datos recogidos previamente, sin ninguna interacción activa con el entorno. Proporciona una forma de utilizar conjuntos de datos previamente recogidos de una variedad de fuentes, incluidas las demostraciones humanas, los experimentos anteriores, las soluciones específicas del dominio e incluso los datos de problemas diferentes pero relacionados, para construir complejos motores de toma de decisiones.
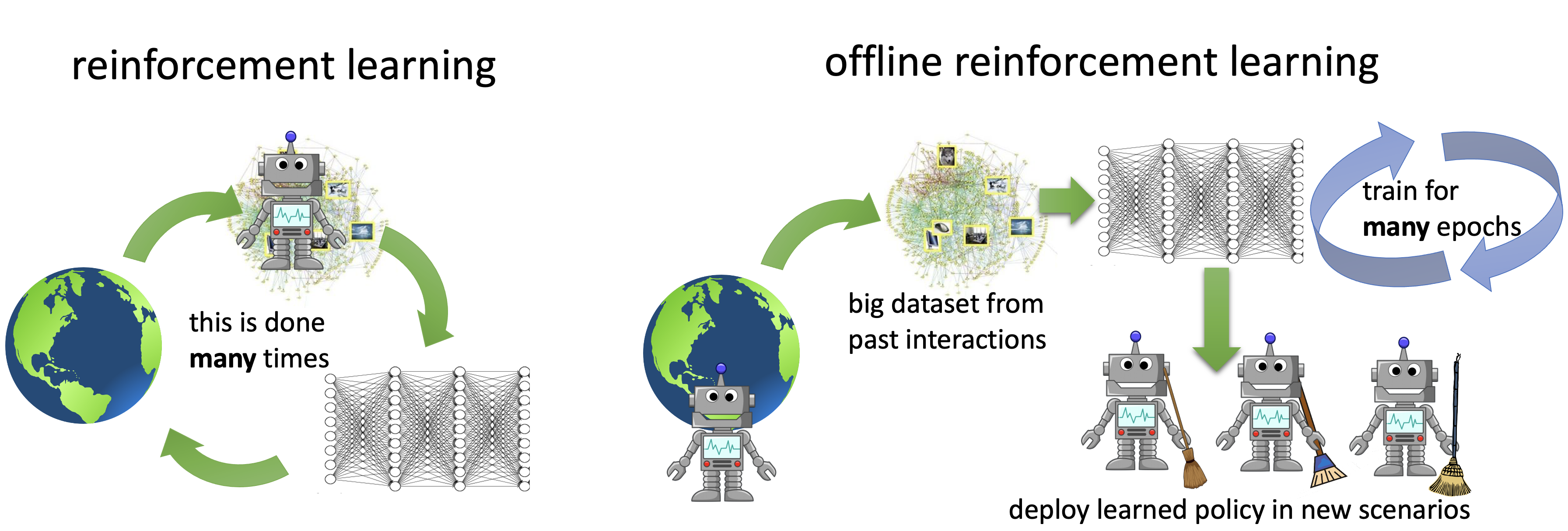
Varios documentos recientes [1] [2] [3] [4] [5] [6]incluyendo nuestro trabajo anterior [7] [8]han discutido que la RL fuera de línea es un problema difícil – requiere manejar los cambios de distribución, que en conjunto con la aproximación de la función y el error de muestreo puede hacer imposible que los métodos estándar de RL [9] [10] …para aprender efectivamente de un conjunto de datos estáticos. Sin embargo, en el último año se han propuesto varios métodos para abordar este problema, y se han hecho progresos sustanciales en este ámbito, tanto en el desarrollo de nuevos algoritmos como en las aplicaciones a problemas del mundo real. En esta entrada del blog, discutiremos dos de nuestros trabajos que avanzan las fronteras de la LR fuera de línea – el aprendizaje conservador de Q (CQL), un algoritmo simple y efectivo para la LR y el COG fuera de línea, un marco de trabajo para el aprendizaje robótico que aprovecha los métodos efectivos de LR fuera de línea como el CQL, para permitir a los agentes conectar los datos del pasado con la experiencia reciente, permitiendo una especie de generalización de «sentido común» cuando el robot tiene la tarea de realizar una tarea bajo una variedad de nuevos escenarios o condiciones iniciales. El principio en el marco del COG también puede aplicarse a otros dominios y no es específico de la robótica.
El principal desafío en la LR fuera de línea es manejar con éxito cambio de distribuciónEl aprendizaje de habilidades efectivas requiere desviarse del comportamiento en el conjunto de datos y hacer predicciones contrafactuales (es decir, responder a preguntas del tipo «qué pasaría si») sobre resultados no vistos. Sin embargo, las predicciones contrafácticas para las decisiones que se desvían demasiado del comportamiento en el conjunto de datos no se pueden hacer de manera fiable. En virtud del procedimiento de actualización estándar de los algoritmos de RL (por ejemplo, la función Q de aprendizaje consulta la función Q en entradas fuera de distribución para calcular el objetivo de arranque durante el entrenamiento), los algoritmos estándar de RL profundos fuera de política tienden a sobrestimar los valores de esos resultados no vistos (como se muestra en la figura siguiente), desviándose así del conjunto de datos para obtener un resultado aparentemente prometedor, pero en realidad terminan fallando como resultado.
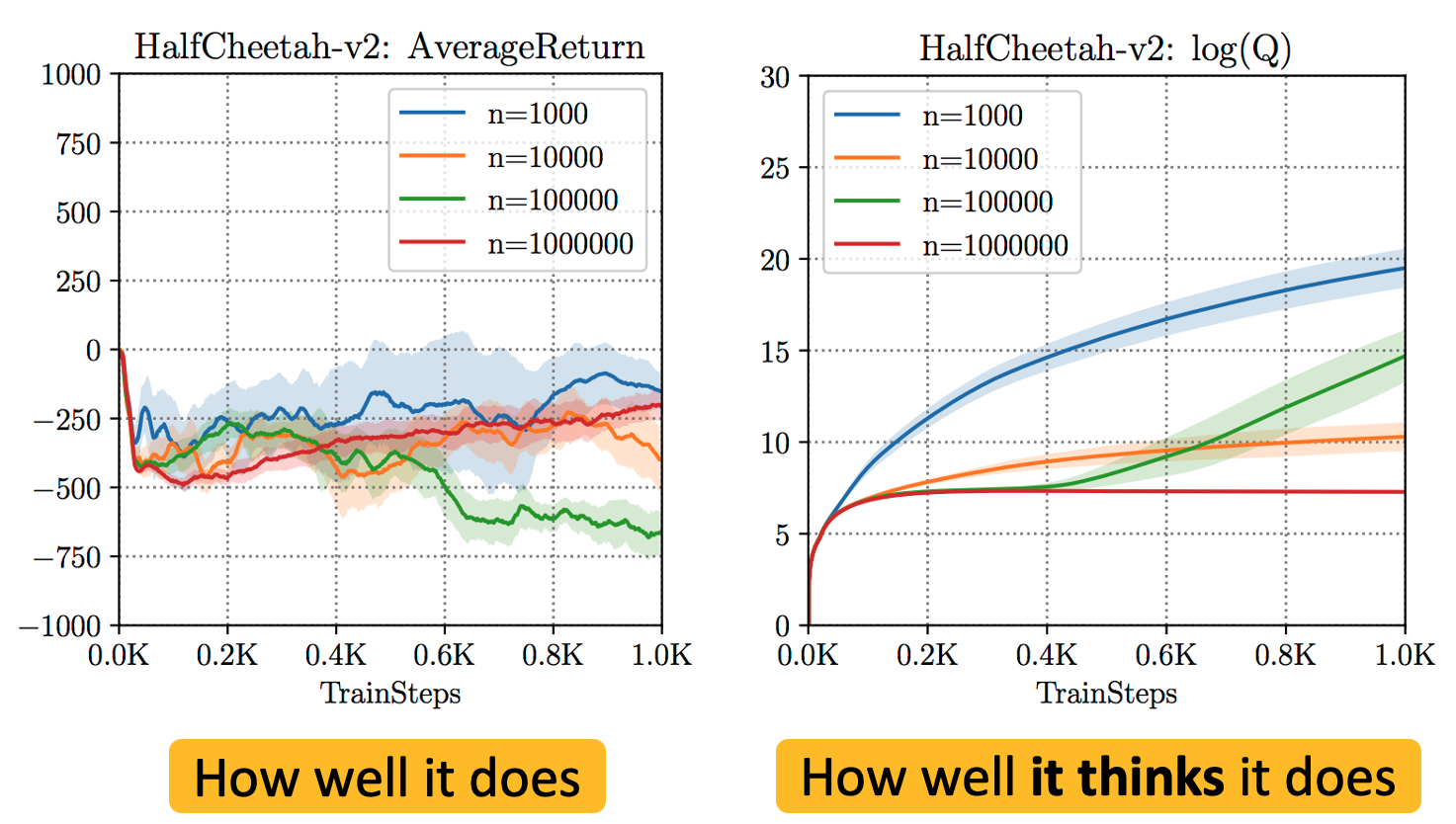
Figura 1: Sobreestimación de los resultados no vistos y no distribuidos cuando los algoritmos estándar de RL profunda fuera de la política (por ejemplo, SAC) se entrenan en conjuntos de datos fuera de línea. Obsérvese que, si bien el rendimiento de la política es negativo en todos los casos, la estimación de la función Q, que es la creencia del algoritmo en su rendimiento, es extremadamente alta ($sim 10^{10}$ en algunos casos).
Funciones Q conservadoras de aprendizaje
Una estrategia «segura» ante tal cambio distributivo es ser conservadorsi estimamos explícitamente el valor de los resultados no vistos de forma conservadora (es decir, les asignamos un valor bajo), entonces el valor estimado o el rendimiento de la política que ejecuta los comportamientos no vistos está garantizado que es pequeño. El uso de tales estimaciones conservadoras para la optimización de la política evitará que la política ejecute acciones no vistas y se desempeñará de manera confiable. El aprendizaje conservador de Q (CQL) hace exactamente esto: aprende una función de valor tal que el rendimiento estimado de la política bajo esta función de valor aprendida baja hasta su valor real. Como se muestra en la figura a continuación, esta propiedad de límite inferior garantiza que no se sobrevalore ningún resultado no visto, lo que evita el principal problema de la LR fuera de línea.
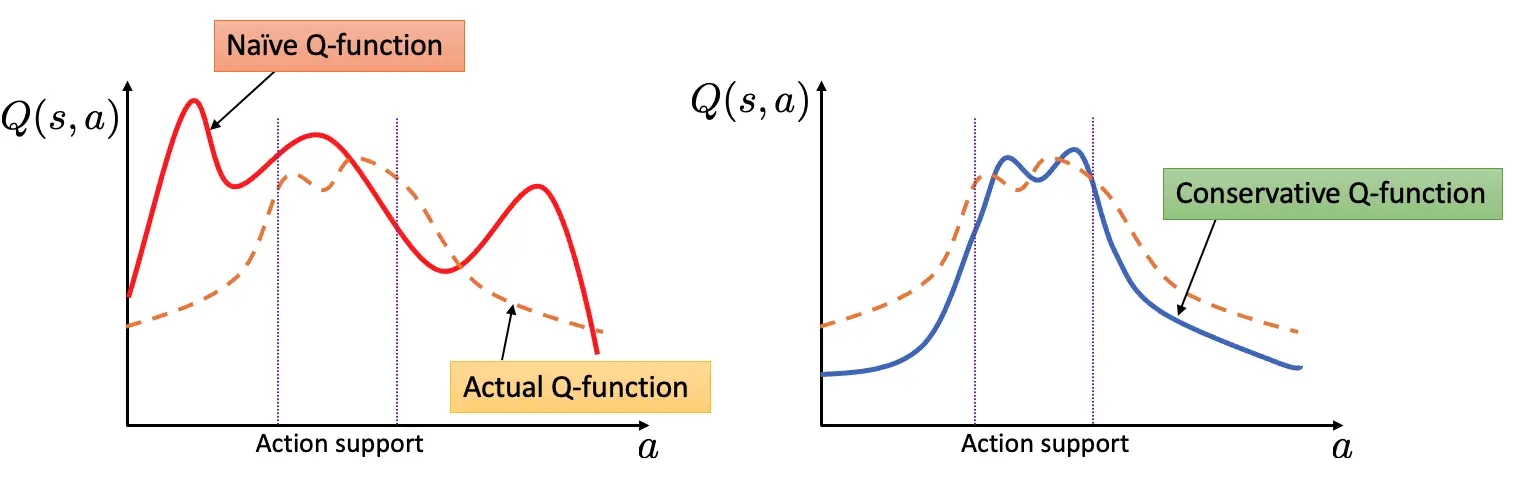
Figura 2: El entrenamiento ingenuo de la función Q puede conducir a la sobreestimación de acciones no vistas (es decir, acciones no en apoyo) que pueden hacer que el comportamiento de bajo rendimiento parezca falsamente prometedor. Al subestimar la función del valor Q para las acciones no vistas en un estado, el CQL asegura que los valores de los comportamientos no vistos no se sobreestimen, dando lugar a la propiedad de bajo rendimiento.
Para obtener este límite inferior en la función de valor Q real de la política, el CQL entrena la función Q utilizando una suma de dos objetivos: el error estándar de TD y un regularizador que minimiza los valores Q en acciones no vistas con valores sobreestimados, mientras que simultáneamente maximiza el valor Q esperado en el conjunto de datos:
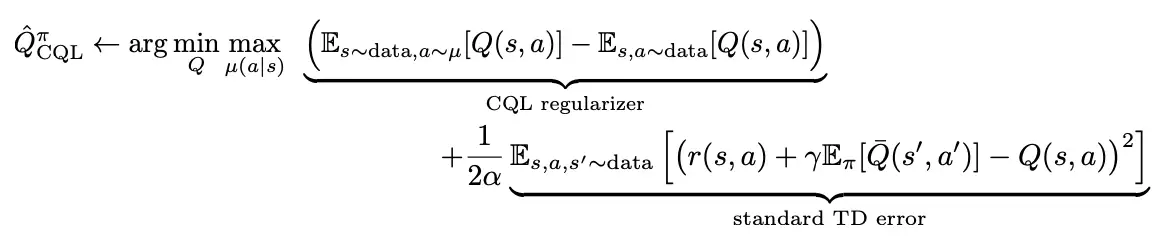
Podemos entonces garantizar que el retorno-estimación de la política aprendida $pi$ bajo $Q^^pi_{\N-texto{CQL}}$ es un límite inferior en el desempeño real de la política:
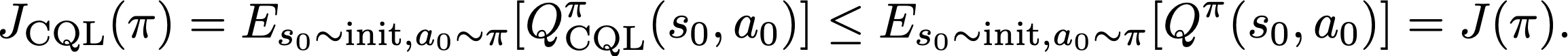
Esto significa que, mediante la adición de un simple regularizador durante el entrenamiento, podemos obtener funciones Q no sobreestimadas, y utilizarlas para la optimización de políticas. El regularizador puede ser estimado usando muestras en el conjunto de datos, y por lo tanto no hay necesidad de una estimación explícita de la política de comportamiento que es requerida por trabajos previos [11] [12] [13]. La estimación de la política de comportamiento no sólo necesita más maquinaria, sino que los errores de estimación inducidos (por ejemplo, cuando la distribución de los datos es difícil de modelar) pueden perjudicar a la RL fuera de línea que utiliza esta estimación [Nair et al. 2020, Ghasemipour et al. 2020]. Además, se puede derivar una amplia familia de instanciamientos algorítmicos de CQL ajustando la forma del regularizador, siempre y cuando se evite la sobreestimación de acciones no vistas.
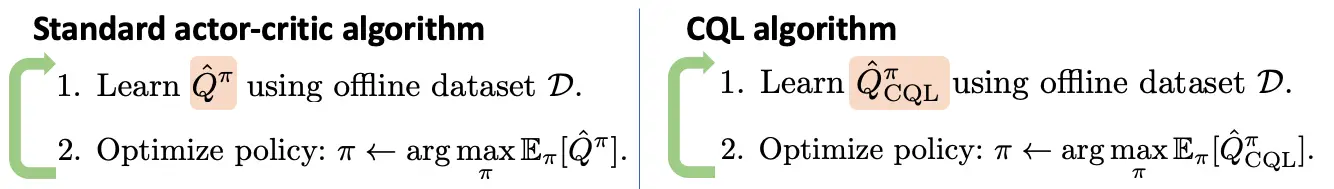
Figura 3: El único cambio introducido en el CQL es un objetivo de entrenamiento modificado para la función Q como se ha destacado anteriormente. Esto hace que sea sencillo utilizar el CQL directamente encima de cualquier implementación estándar de Q-learning profundo o de crítica de actores.
Una vez que se obtiene una estimación conservadora del valor de la política $Q^pi_{text{CQL}}$, CQL simplemente conecta esta estimación en un método de aprendizaje de actor crítico o Q-learning, como se muestra arriba, y actualiza $pi$ hacia la maximización de la función Q conservadora.
Entonces, ¿qué tan bien se desempeña el CQL?
Evaluamos el CQL en varios dominios, incluyendo los juegos Atari basados en imágenes y también varias tareas del benchmark D4RL. Aquí presentamos los resultados del dominio Ant Maze del benchmark D4RL. El objetivo de estas tareas es navegar la hormiga desde un estado inicial hasta un estado final. El conjunto de datos fuera de línea consiste en movimientos aleatorios de la hormiga, pero no hay una sola trayectoria que resuelva la tarea. Cualquier algoritmo exitoso necesita «coser» diferentes sub-trayectorias para lograr el éxito. Mientras que los métodos anteriores (BC, SAC, BCQ, BEAR, BRAC, AWR, AlgaeDICE) funcionan razonablemente en el fácil laberinto en U, son incapaces de coser trayectorias en los laberintos más difíciles. De hecho, el CQL es el único algoritmo que hace progresos no triviales y obtiene >50% y >14% tasas de éxito en laberintos medianos y grandes. Esto se debe a que la limitación de la política aprendida al conjunto de datos de forma explícita, como se hizo en los métodos anteriores, tiende a ser demasiado conservadora: no es necesario limitar las acciones a los datos si las acciones no vistas tienen bajos valores Q aprendidos. Dado que el CQL impone un regularizador «consciente del valor», evita este exceso de conservadurismo.
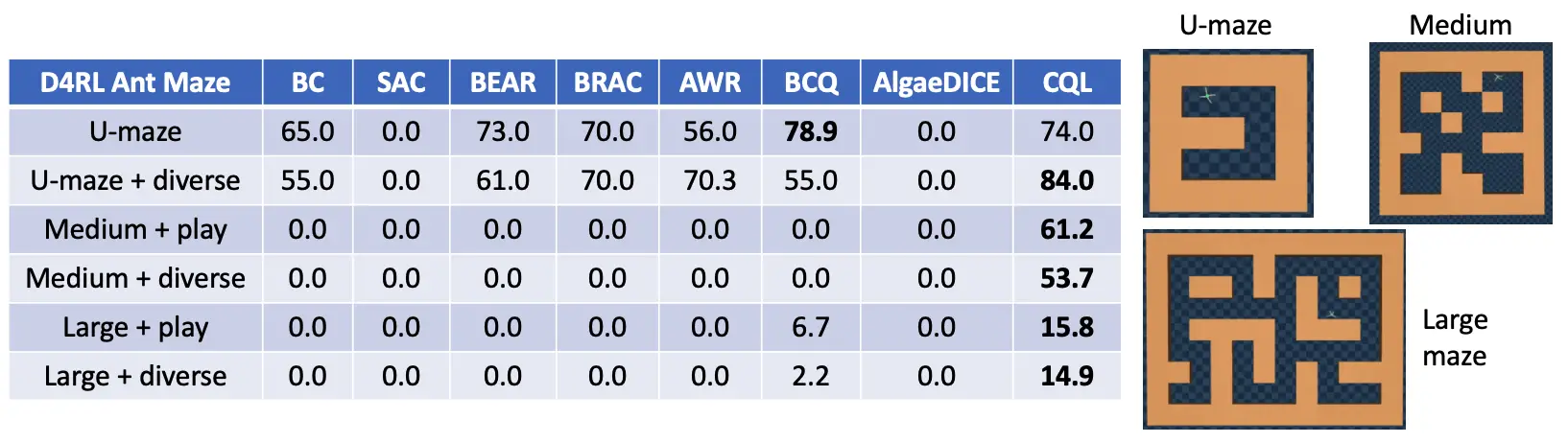
Figura 4: Rendimiento del CQL y otros algoritmos de RL fuera de línea medidos en términos de tasa de éxito (rango [0, 100]) en la tarea de navegación de la hormiga de D4RL. Observe que el CQL supera los métodos anteriores en los dominios de laberinto más duros por márgenes no triviales.
En los juegos Atari basados en imágenes, observamos que el CQL supera a los métodos anteriores (QR-DQN, REM) en algunos casos por enormes márgenes, por ejemplo por un factor de 5x y 36x en Breakout y Q$^*$bert respectivamente, indicando que el CQL es un algoritmo prometedor tanto para el control continuo como para las tareas de acción discreta, y funciona no sólo desde el estado de baja dimensión, sino también desde las observaciones de imagen en bruto.
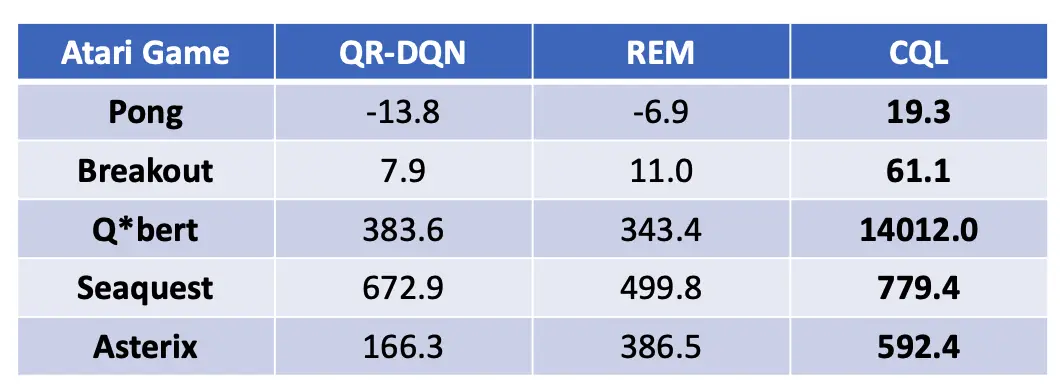
Figura 5: Rendimiento del CQL en cinco juegos Atari. Tenga en cuenta que el CQL supera los métodos anteriores: QR-DQN y REM que se han aplicado en esta configuración por 36x en Q*bert y 5x en Breakout.
La mayoría de los avances en la LR fuera de línea han sido evaluados en los puntos de referencia estándar de la LR (incluyendo CQL, como se discutió anteriormente), pero ¿están estos algoritmos listos para abordar el tipo de problemas del mundo real que motivan la investigación en la LR fuera de línea en primer lugar? Una importante capacidad que la LR fuera de línea promete sobre otros enfoques para la toma de decisiones es la capacidad de ingerir grandes y diversos conjuntos de datos y producir soluciones que se generalizan ampliamente a nuevos escenarios. Por ejemplo, las políticas que son eficaces para recomendar videos a un nuevo usuario o políticas que pueden ejecutar tareas robóticas en nuevo escenarios. La capacidad de generalizar es esencial en casi cualquier sistema de aprendizaje de máquinas que podamos construir, pero las típicas tareas de referencia de RL no ponen a prueba esta propiedad. Damos un paso adelante para abordar este tema y mostramos que principios simples y agnósticos de dominio aplicados sobre métodos efectivos de RL fuera de línea, pueden ser muy efectivos para permitir “sentido común” generalización en los sistemas de IA.
El COG es un marco algorítmico para utilizar grandes conjuntos de datos no etiquetados de comportamiento diverso para aprender políticas generalizables a través de RL fuera de línea. Como ejemplo motivador, consideremos un robot que ha sido entrenado para sacar un objeto de un cajón abierto (mostrado abajo). Es probable que este robot falle cuando se lo coloque en una escena en la que el cajón esté en cambio cerrado, ya que no ha visto este escenario (o condición inicial) antes.


Figura 6: Izquierda: Vemos un robot que ha aprendido a sacar un objeto de un cajón abierto. Derecha: Sin embargo, el mismo robot no realiza la tarea si el cajón está cerrado al principio del episodio.
Sin embargo, nos gustaría que nuestra política aprendida permitiera ejecutar la tarea a partir de tantas condiciones iniciales diferentes como sea posible. Una simple condición nueva podría consistir en un cajón cerrado, mientras que condiciones nuevas más complicadas en las que el cajón está bloqueado por un objeto, o por otro cajón también son posibles. ¿Podemos aprender políticas que puedan realizar tareas a partir de condiciones iniciales variadas?



Figura 7: De L a R: cajón cerrado, cajón bloqueado por un objeto, cajón bloqueado por otro cajón.
Formalizando el ajuste: Aprovechar la experiencia del pasado de las tareas agnósticas
De manera similar a los escenarios del mundo real en los que se dispone de grandes conjuntos de datos sin etiquetar junto con datos limitados de tareas específicas, nuestro agente dispone de dos tipos de conjuntos de datos. El conjunto de datos específicos de la tarea consiste en el comportamiento relevante para la tarea, pero el conjunto de datos anterior puede consistir en un número de comportamientos aleatorios o de guión que se ejecutan en el mismo entorno/juego. Si un subconjunto de este conjunto de datos previo es útil para ampliar nuestra habilidad (que se muestra en azul más abajo), podemos aprovecharlo para aprender una política que pueda resolver la tarea a partir de nuevas condiciones iniciales. Obsérvese que no todos los datos anteriores tienen que ser útiles para la tarea posterior (que se muestra en rojo a continuación), y tampoco necesitamos que este conjunto de datos anteriores tenga etiquetas o recompensas explícitas. Nuestro objetivo es utilizar tanto los datos previos como los datos específicos de la tarea para aprender una política que pueda ejecutar la tarea a partir de las condiciones iniciales que no se vieron en los datos de la tarea.
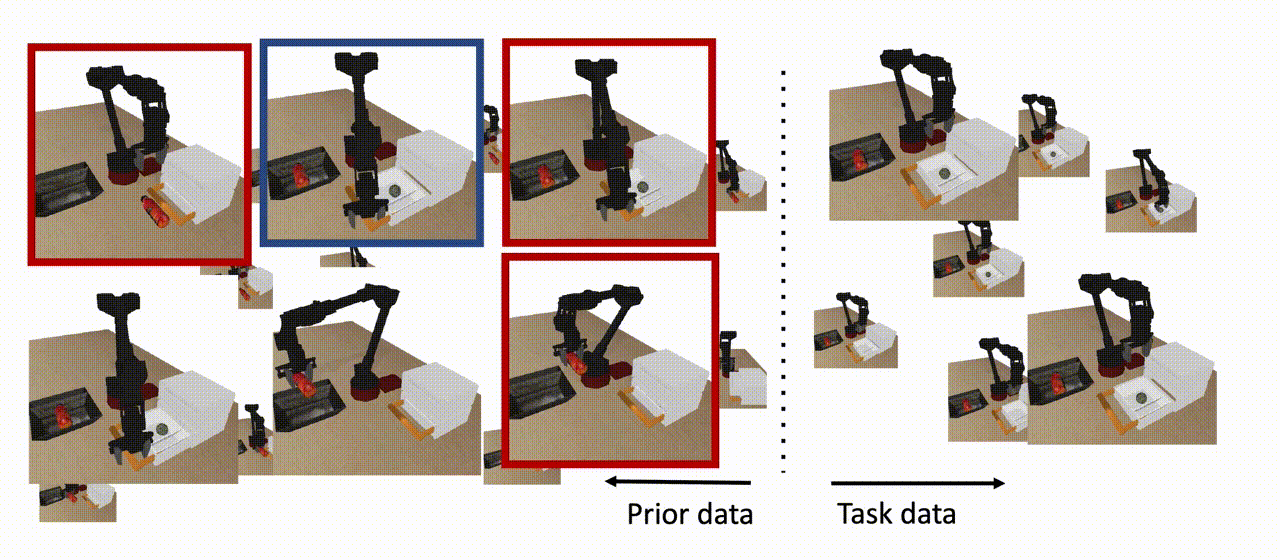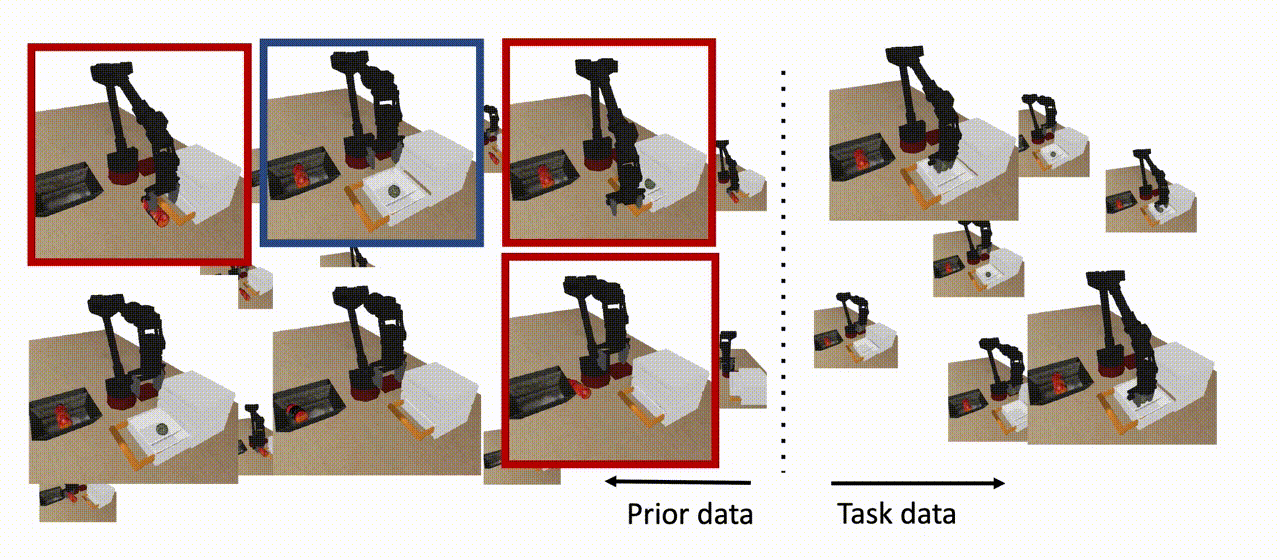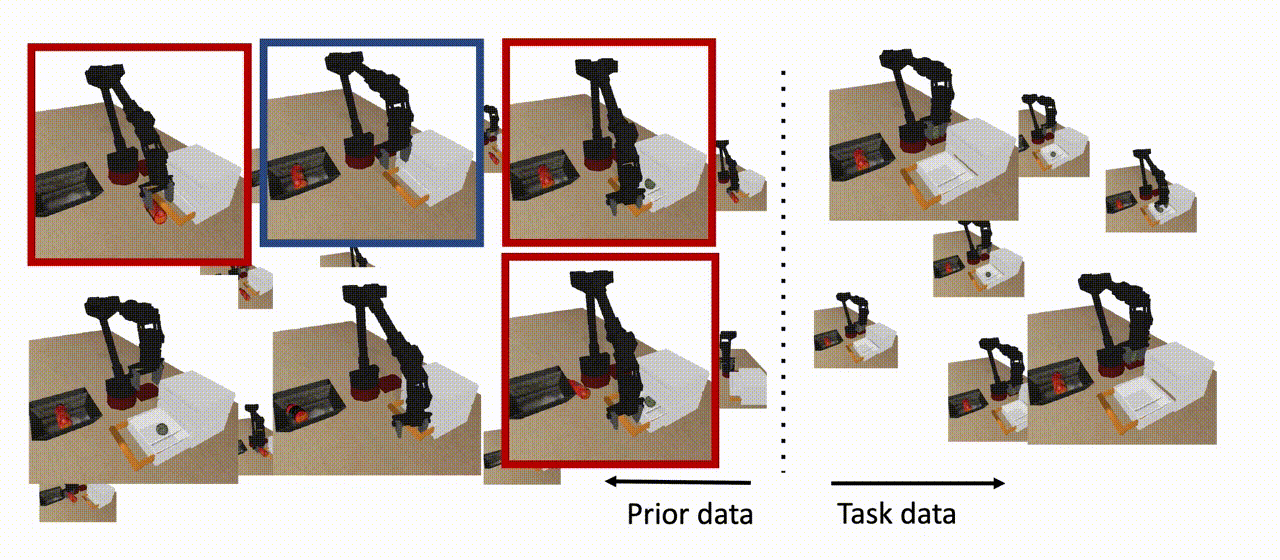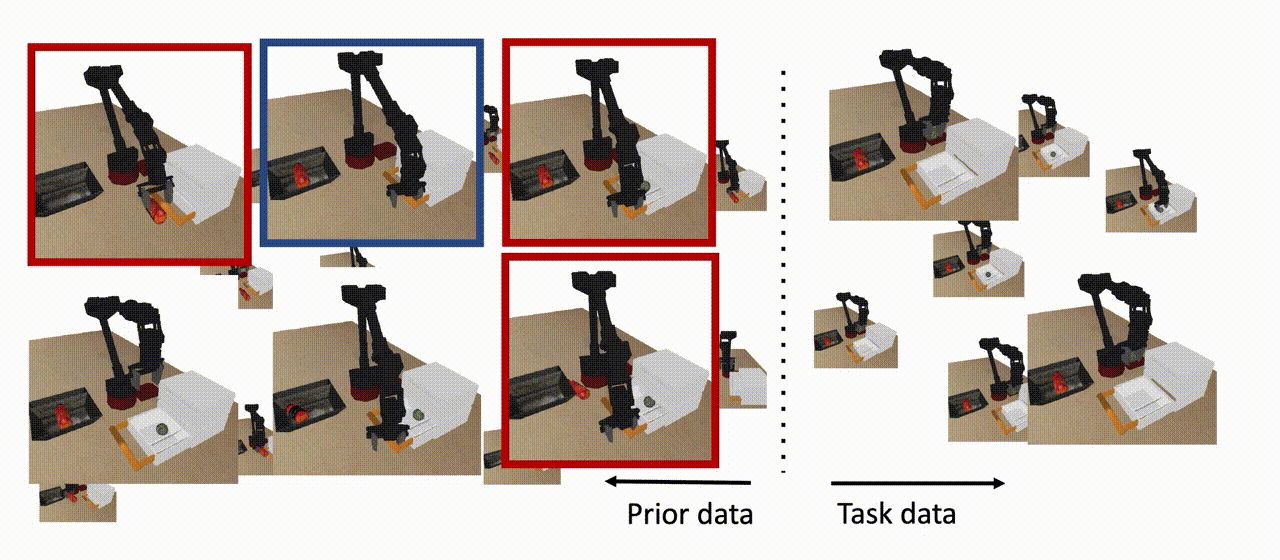
Figura 8: El COG utiliza datos previos para aprender una política que pueda resolver la tarea a partir de condiciones iniciales que no se vieron en los datos de la tarea, siempre y cuando un subconjunto de los datos previos contenga un comportamiento que ayude a extender la habilidad (se muestra en azul). Nótese que no todos los datos previos necesitan estar en apoyo de la habilidad descendente (mostrados en rojo), y tampoco necesitamos ninguna etiqueta de recompensa para este conjunto de datos.
Conectando habilidades a través de RL fuera de línea
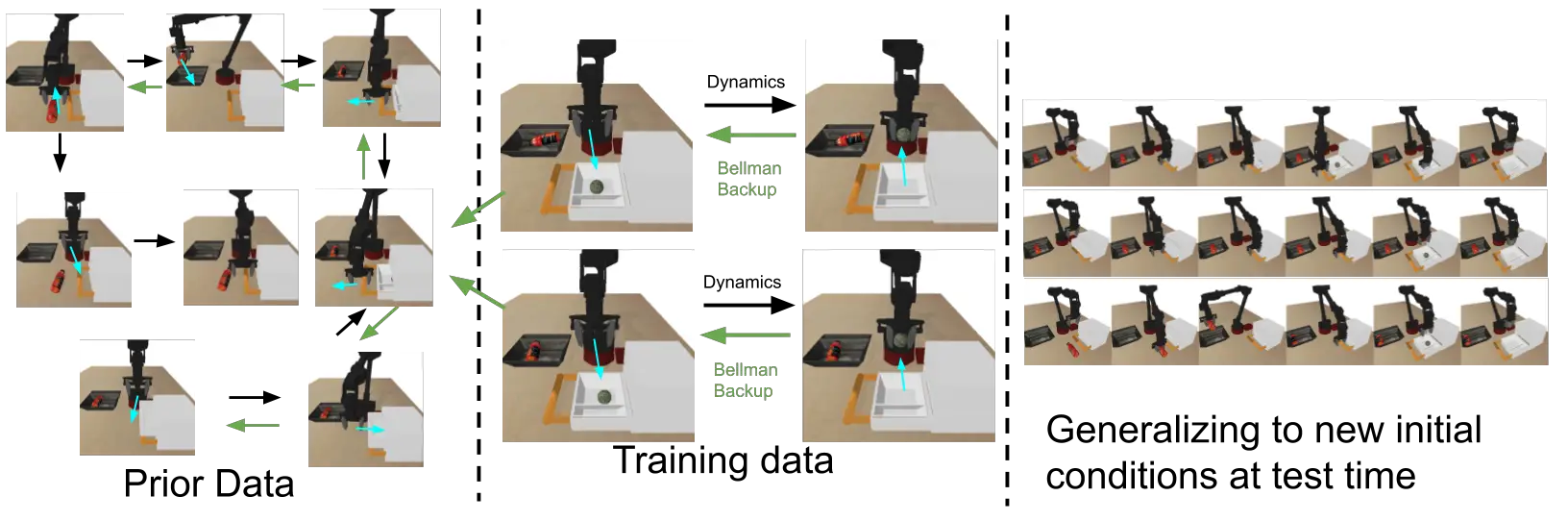
Figura 9: Las flechas negras denotan la dinámica del MDP. Las flechas verdes denotan la propagación de los valores Q desde los estados de alta recompensa a los estados más alejados de la meta.
Comenzamos ejecutando el aprendizaje de Q fuera de línea (CQL) en los datos de la tarea, lo que permite que los valores Q se propaguen desde los estados de alta recompensa a los estados más alejados de la meta. Luego añadimos el conjunto de datos anterior al buffer de entrenamiento, asignando a todas las transiciones una recompensa cero. La programación dinámica adicional (fuera de línea) en este conjunto de datos ampliado permite que los valores Q se propaguen a condiciones iniciales que no se vieron en los datos de la tarea, dando lugar a políticas que son exitosas a partir de nuevas condiciones iniciales. Nótese que no hay una sola trayectoria en nuestro conjunto de datos que resuelva toda la tarea a partir de estas nuevas condiciones iniciales, pero el aprendizaje de Q fuera de línea nos permite «coser» subtrayectorias relevantes a partir de los datos anteriores y de la tarea, sin ninguna supervisión adicional. Encontramos que los métodos eficaces de RL fuera de línea (por ejemplo, CQL) son esenciales para obtener un buen rendimiento, y que los métodos anteriores fuera de línea o fuera de línea (por ejemplo, BEAR, AWR) no funcionaban bien en estas tareas. A continuación se muestran algunos ejemplos de nuestra política aprendida para la tarea de agarre de cajones. Nuestro método es capaz de unir varios comportamientos para resolver la tarea de abajo. Por ejemplo, en el segundo vídeo de abajo: la política es capaz de elegir un objeto de bloqueo, guardarlo, abrir el cajón y sacar un objeto. Obsérvese que el agente está realizando esta tarea a partir de observaciones de imágenes (que se muestran en la esquina superior derecha), y recibe una recompensa de +1 sólo después de terminar el último paso (las recompensas son iguales a cero en todas las demás).



Figura 10: El desempeño de nuestra política aprendida para condiciones iniciales novedosas.
Un resultado real del robot
También evaluamos nuestro método en un robot real, donde vemos que nuestra política aprendida es capaz de abrir un cajón y sacar un objeto, aunque nunca vio una sola trayectoria ejecutando toda la tarea durante el entrenamiento. Nuestro método tiene éxito en 7 de 8 mientras que nuestra línea de base más fuerte basada en la clonación de comportamiento fue incapaz de resolver la tarea ni siquiera para un solo ensayo. Aquí hay algunos ejemplos de nuestra política de aprendizaje.



En el último año, hemos tomado medidas para desarrollar algoritmos de RL fuera de línea que puedan manejar mejor las complejidades del mundo real, como las distribuciones de datos multimodales, observaciones de imágenes en bruto, conjuntos de datos previos diversos y agnósticos de tareas, etc. Sin embargo, siguen abiertos varios problemas difíciles. Al igual que los métodos de aprendizaje supervisado, los algoritmos de RL fuera de línea también pueden «sobreajustarse» como resultado de un entrenamiento excesivo en el conjunto de datos. La naturaleza de esta «sobrecarga» es compleja, puede manifestarse como una solución demasiado conservadora y demasiado optimista. En varios casos, este fenómeno de «sobreajuste» da lugar a redes neuronales mal acondicionadas (por ejemplo, redes que sobrevaloran las predicciones) y actualmente falta una comprensión exacta de este fenómeno. Así pues, una interesante vía para la labor futura es concebir métodos de selección de modelos que puedan utilizarse para la selección de los puntos de control de las políticas o la detención temprana, mitigando así esta cuestión. Otra vía es comprender las causas del origen de este problema de «sobreajuste» y utilizar los conocimientos adquiridos para mejorar directamente la estabilidad de los algoritmos de RL fuera de línea.
Por último, a medida que avanzamos gradualmente hacia los entornos del mundo real, las áreas relacionadas de aprendizaje auto-supervisado, aprendizaje de representación, aprendizaje de transferencia, meta-aprendizaje, etc., serán esenciales para aplicarlas conjuntamente con los algoritmos de RL fuera de línea, especialmente en entornos con datos limitados. Esto motiva naturalmente varias cuestiones teóricas y empíricas: ¿Qué esquemas de aprendizaje de representación son óptimos para los métodos de RL fuera de línea? ¿Qué tan bien funcionan los métodos de RL fuera de línea cuando se utilizan las funciones de recompensa aprendidas de los datos? ¿Qué constituye un conjunto de tareas susceptibles de ser transferidas en la RL fuera de línea? Esperamos con interés los progresos en esta área durante el próximo año.
Agradecemos a Sergey Levine, George Tucker, Glen Berseth, Marvin Zhang, Dhruv Shah y Gaoyoue Zhou por sus valiosos comentarios en las versiones anteriores de este post.
Esta entrada en el blog se basa en dos documentos que aparecerán en la conferencia/talleres de NeurIPS este año. Le invitamos a venir y discutir estos temas con nosotros en NeurIPS.
-
Q-Learning conservador para el aprendizaje de refuerzo fuera de línea
Aviral KumarAurick Zhou, George Tucker, Sergey Levine.
En Avances en los Sistemas de Procesamiento de Información Neural (NeurIPS), 2020.
[paper] [code] [project page] -
COG: Conectando las nuevas habilidades con la experiencia pasada con el aprendizaje de refuerzo fuera de línea
Avi Singh…Albert Yu, Jonathan Yang, Jesse Zhang, Aviral KumarSergey Levine.
En la Conferencia sobre Aprendizaje Robótico (CDR) 2020.
Contribuyó a la charla en el Taller de RL Offline, NeurIPS 2020.
[paper] [code] [project page]
