Última actualización el 27 de abril de 2021
Descenso de gradiente es un algoritmo de optimización que sigue el gradiente negativo de una función objetivo para localizar el mínimo de la función.
Es una técnica simple y efectiva que se puede implementar con solo unas pocas líneas de código. También proporciona la base para muchas extensiones y modificaciones que pueden resultar en un mejor rendimiento. El algoritmo también proporciona la base para la extensión ampliamente utilizada llamada descenso de gradiente estocástico, que se utiliza para entrenar redes neuronales de aprendizaje profundo.
En este tutorial, descubrirá cómo implementar la optimización del descenso de gradientes desde cero.
Después de completar este tutorial, sabrá:
- El descenso de gradiente es un procedimiento general para optimizar una función objetivo diferenciable.
- Cómo implementar el algoritmo de descenso de gradientes desde cero en Python.
- Cómo aplicar el algoritmo de descenso de gradiente a una función objetivo.
Empecemos.

Cómo implementar la optimización del descenso de gradientes desde cero
Foto de Bernd Thaller, algunos derechos reservados.
Descripción general del tutorial
Este tutorial se divide en tres partes; ellos son:
- Descenso de gradiente
- Algoritmo de descenso de gradiente
- Ejemplo resuelto de descenso de gradiente
Optimización del descenso de gradientes
El descenso de gradientes es un algoritmo de optimización.
Técnicamente se le conoce como un algoritmo de optimización de primer orden, ya que hace uso explícito de la derivada de primer orden de la función objetivo de destino.
Los métodos de primer orden se basan en la información del gradiente para ayudar a dirigir la búsqueda de un mínimo …
– Página 69, Algoritmos de optimización, 2019.
La derivada de primer orden, o simplemente la «derivada», es la tasa de cambio o pendiente de la función objetivo en un punto específico, p. Ej. para una entrada específica.
Si la función de destino toma múltiples variables de entrada, se denomina función multivariante y las variables de entrada se pueden considerar como un vector. A su vez, la derivada de una función objetivo multivariante también se puede tomar como un vector y se denomina generalmente «gradiente».
- Degradado: Derivada de primer orden para una función objetivo multivariante.
La derivada o el gradiente apunta en la dirección del ascenso más pronunciado de la función de destino para una entrada.
El gradiente apunta en la dirección del ascenso más pronunciado del hiperplano tangente …
– Página 21, Algoritmos de optimización, 2019.
Específicamente, el signo del gradiente le dice si la función de destino está aumentando o disminuyendo en ese punto.
- Gradiente positivo: La función está aumentando en ese punto.
- Gradiente negativo: La función está disminuyendo en ese punto.
El descenso de gradiente se refiere a un algoritmo de optimización de minimización que sigue el negativo del gradiente cuesta abajo de la función objetivo para localizar el mínimo de la función.
De manera similar, podemos referirnos al ascenso de gradiente para la versión de maximización del algoritmo de optimización que sigue el gradiente cuesta arriba hasta el máximo de la función objetivo.
- Descenso de gradiente: Optimización de minimización que sigue el negativo del gradiente al mínimo de la función objetivo.
- Ascenso en gradiente: Optimización de maximización que sigue el gradiente al máximo de la función objetivo.
Un aspecto fundamental de los algoritmos de descenso de gradientes es la idea de seguir el gradiente de la función objetivo.
Por definición, el algoritmo de optimización solo es apropiado para funciones de destino donde la función derivada está disponible y se puede calcular para todos los valores de entrada. Esto no se aplica a todas las funciones de destino, solo a las llamadas funciones diferenciables.
El principal beneficio del algoritmo de descenso de gradiente es que es fácil de implementar y eficaz en una amplia gama de problemas de optimización.
Los métodos de degradado son simples de implementar y, a menudo, funcionan bien.
– Página 115, Introducción a la optimización, 2001.
El descenso de gradiente se refiere a una familia de algoritmos que utilizan la derivada de primer orden para navegar al óptimo (mínimo o máximo) de una función objetivo.
Hay muchas extensiones del enfoque principal que normalmente reciben el nombre de la característica agregada al algoritmo, como el descenso de gradiente con impulso, el descenso de gradiente con gradientes adaptativos, etc.
El descenso de gradiente también es la base del algoritmo de optimización utilizado para entrenar redes neuronales de aprendizaje profundo, denominado descenso de gradiente estocástico o SGD. En esta variación, la función objetivo es una función de error y el gradiente de la función se aproxima a partir del error de predicción en muestras del dominio del problema.
Ahora que estamos familiarizados con una idea de alto nivel de la optimización del descenso de gradientes, veamos cómo podríamos implementar el algoritmo.
Algoritmo de descenso de gradiente
En esta sección, veremos más de cerca el algoritmo de descenso de gradiente.
El algoritmo de descenso de gradiente requiere una función objetivo que se está optimizando y la función derivada para la función objetivo.
La función objetivo F() devuelve una puntuación para un conjunto dado de entradas y la función derivada F'() da la derivada de la función objetivo para un conjunto dado de entradas.
- Función objetiva: Calcula una puntuación para un conjunto determinado de parámetros de entrada.
Función derivada: Calcula la derivada (gradiente) de la función objetivo para un conjunto de entradas dado.
El algoritmo de descenso de gradiente requiere un punto de partida (X) en el problema, como un punto seleccionado al azar en el espacio de entrada.
Luego se calcula la derivada y se da un paso en el espacio de entrada que se espera que resulte en un movimiento cuesta abajo en la función objetivo, asumiendo que estamos minimizando la función objetivo.
Un movimiento cuesta abajo se realiza calculando primero qué tan lejos moverse en el espacio de entrada, calculado como el tamaño del paso (llamado alfa o la tasa de aprendizaje) multiplicado por el gradiente. Esto luego se resta del punto actual, asegurando que nos movemos contra el gradiente o hacia abajo de la función de destino.
- x_nuevo = x – alfa * f ‘(x)
Cuanto más pronunciada sea la función objetivo en un punto dado, mayor será la magnitud del gradiente y, a su vez, mayor será el paso dado en el espacio de búsqueda.
El tamaño del paso realizado se escala mediante un hiperparámetro de tamaño de paso.
- Numero de pie (alfa): Hiperparámetro que controla qué tan lejos moverse en el espacio de búsqueda contra el gradiente en cada iteración del algoritmo.
Si el tamaño del paso es demasiado pequeño, el movimiento en el espacio de búsqueda será pequeño y la búsqueda llevará mucho tiempo. Si el tamaño del paso es demasiado grande, la búsqueda puede rebotar en el espacio de búsqueda y omitir los óptimos.
Tenemos la opción de dar pasos muy pequeños y reevaluar el gradiente en cada paso, o podemos dar pasos grandes cada vez. El primer enfoque da como resultado un método laborioso para llegar al minimizador, mientras que el segundo enfoque puede resultar en un camino más en zigzag hacia el minimizador.
– Página 114, Introducción a la optimización, 2001.
Encontrar un buen tamaño de paso puede requerir algo de prueba y error para la función de destino específica.
La dificultad de elegir el tamaño del paso puede dificultar la búsqueda del óptimo exacto de la función de destino. Muchas extensiones implican adaptar la tasa de aprendizaje a lo largo del tiempo para dar pasos más pequeños o pasos de diferentes tamaños en diferentes dimensiones y así sucesivamente para permitir que el algoritmo se concentre en la función óptima.
El proceso de calcular la derivada de un punto y calcular un nuevo punto en el espacio de entrada se repite hasta que se cumple alguna condición de parada. Esto podría ser un número fijo de pasos o evaluaciones de la función objetivo, una falta de mejora en la evaluación de la función objetivo durante cierto número de iteraciones o la identificación de un área plana (estacionaria) del espacio de búsqueda representada por un gradiente de cero.
- Condición de parada: Decisión de cuándo finalizar el procedimiento de búsqueda.
Veamos cómo podríamos implementar el algoritmo de descenso de gradientes en Python.
Primero, podemos definir un punto inicial como un punto seleccionado al azar en el espacio de entrada definido por límites.
Los límites se pueden definir junto con una función objetivo como una matriz con un valor mínimo y máximo para cada dimensión. La función rand () NumPy se puede utilizar para generar un vector de números aleatorios en el rango 0-1.
|
... # generar un punto inicial solución = límites[[:, 0] + rand(len(límites)) * (límites[[:, 1] – límites[[:, 0]) |
Luego podemos calcular la derivada del punto usando una función llamada derivado().
|
... # calcular gradiente degradado = derivado(solución) |
Y da un paso en el espacio de búsqueda hacia un nuevo punto cuesta abajo del punto actual.
La nueva posición se calcula utilizando el gradiente calculado y la Numero de pie hiperparámetro.
|
... # Da un paso solución = solución – Numero de pie * degradado |
Luego podemos evaluar este punto e informar el desempeño.
|
... # evaluar el punto candidato solution_eval = objetivo(solución) |
Este proceso se puede repetir para un número fijo de iteraciones controladas mediante un nitro hiperparámetro.
|
... # ejecutar el descenso de gradiente por I en distancia(nitro): # calcular gradiente degradado = derivado(solución) # Da un paso solución = solución – Numero de pie * degradado # evaluar el punto candidato solution_eval = objetivo(solución) # informe de progreso impresión(‘>% d f (% s) =% .5f’ % (I, solución, solution_eval)) |
Podemos unir todo esto en una función llamada descenso de gradiente().
La función toma el nombre de las funciones objetivo y de gradiente, así como los límites de las entradas de la función objetivo, el número de iteraciones y el tamaño del paso, luego devuelve la solución y su evaluación al final de la búsqueda.
El algoritmo de optimización de descenso de gradiente completo implementado como una función se enumera a continuación.
|
# algoritmo de descenso de gradiente def descenso de gradiente(objetivo, derivado, límites, nitro, Numero de pie): # generar un punto inicial solución = límites[[:, 0] + rand(len(límites)) * (límites[[:, 1] – límites[[:, 0]) # ejecutar el descenso de gradiente por I en distancia(nitro): # calcular gradiente degradado = derivado(solución) # Da un paso solución = solución – Numero de pie * degradado # evaluar el punto candidato solution_eval = objetivo(solución) # informe de progreso impresión(‘>% d f (% s) =% .5f’ % (I, solución, solution_eval)) regreso [[solución, solution_eval] |
Ahora que estamos familiarizados con el algoritmo de descenso de gradientes, veamos un ejemplo trabajado.
Ejemplo resuelto de descenso de gradiente
En esta sección, trabajaremos a través de un ejemplo de aplicación de descenso de gradiente a una función de optimización de prueba simple.
Primero, definamos una función de optimización.
Usaremos una función unidimensional simple que cuadra la entrada y define el rango de entradas válidas de -1.0 a 1.0.
La objetivo() función a continuación implementa esta función.
|
# función objetiva def objetivo(X): regreso X**2.0 |
Luego, podemos muestrear todas las entradas en el rango y calcular el valor de la función objetivo para cada una.
|
... # definir rango para entrada r_min, r_max = –1.0, 1.0 # rango de entrada de muestra uniformemente en incrementos de 0.1 entradas = arange(r_min, r_max+0,1, 0,1) # calcular objetivos resultados = objetivo(entradas) |
Finalmente, podemos crear una gráfica de línea de las entradas (eje x) versus los valores de la función objetivo (eje y) para obtener una intuición de la forma de la función objetivo que buscaremos.
|
... # crear una gráfica de línea de entrada vs resultado pyplot.gráfico(entradas, resultados) # mostrar la trama pyplot.show() |
El siguiente ejemplo une esto y proporciona un ejemplo de cómo trazar la función de prueba unidimensional.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 |
# gráfico de función simple de numpy importar arange de matplotlib importar pyplot # función objetiva def objetivo(X): regreso X**2.0 # definir rango para entrada r_min, r_max = –1.0, 1.0 # rango de entrada de muestra uniformemente en incrementos de 0.1 entradas = arange(r_min, r_max+0,1, 0,1) # calcular objetivos resultados = objetivo(entradas) # crear una gráfica de línea de entrada vs resultado pyplot.gráfico(entradas, resultados) # mostrar la trama pyplot.show() |
La ejecución del ejemplo crea un gráfico de líneas de las entradas de la función (eje x) y la salida calculada de la función (eje y).
Podemos ver la familiar forma de U llamada parábola.
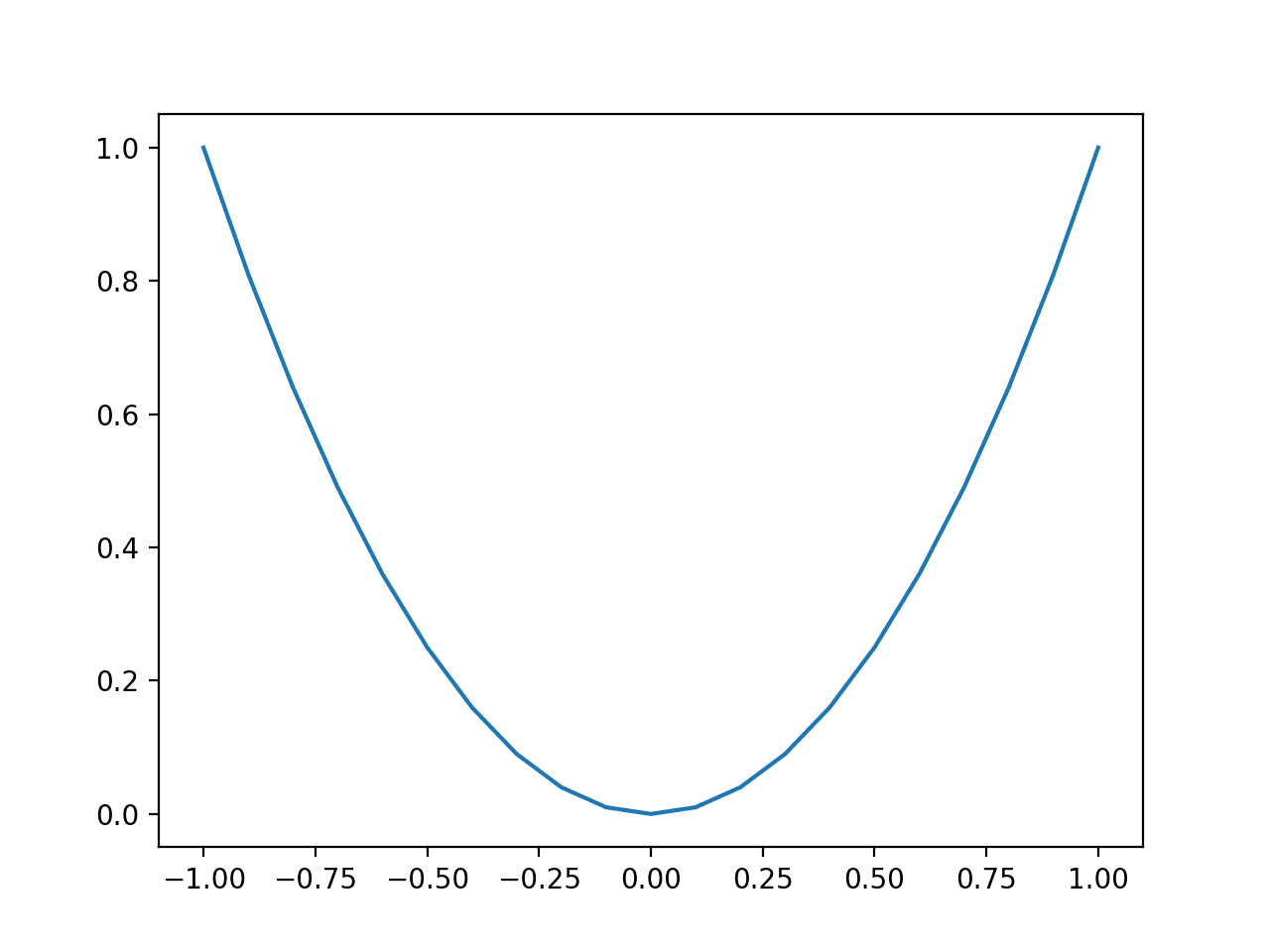
Gráfico de línea de función unidimensional simple
A continuación, podemos aplicar el algoritmo de descenso de gradiente al problema.
Primero, necesitamos una función que calcule la derivada de esta función.
La derivada de x ^ 2 es x * 2 y la derivado() La función implementa esto a continuación.
|
# derivada de la función objetivo def derivado(X): regreso X * 2.0 |
Luego podemos definir los límites de la función objetivo, el tamaño del paso y el número de iteraciones del algoritmo.
Usaremos un tamaño de paso de 0.1 y 30 iteraciones, ambas encontradas después de un poco de experimentación.
|
... # definir rango para entrada límites = asarray([[[[–1.0, 1.0]]) # definir las iteraciones totales nitro = 30 # definir el tamaño máximo de paso Numero de pie = 0,1 # realizar la búsqueda de descenso de gradiente mejor, puntaje = descenso de gradiente(objetivo, derivado, límites, nitro, Numero de pie) |
Uniendo esto, el ejemplo completo de aplicación de la optimización del descenso de gradiente a nuestra función de prueba unidimensional se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
# ejemplo de descenso de gradiente para una función unidimensional de numpy importar asarray de numpy.aleatorio importar rand # función objetiva def objetivo(X): regreso X**2.0 # derivada de la función objetivo def derivado(X): regreso X * 2.0 # algoritmo de descenso de gradiente def descenso de gradiente(objetivo, derivado, límites, nitro, Numero de pie): # generar un punto inicial solución = límites[[:, 0] + rand(len(límites)) * (límites[[:, 1] – límites[[:, 0]) # ejecutar el descenso de gradiente por I en distancia(nitro): # calcular gradiente degradado = derivado(solución) # Da un paso solución = solución – Numero de pie * degradado # evaluar el punto candidato solution_eval = objetivo(solución) # informe de progreso impresión(‘>% d f (% s) =% .5f’ % (I, solución, solution_eval)) regreso [[solución, solution_eval] # definir rango para entrada límites = asarray([[[[–1.0, 1.0]]) # definir las iteraciones totales nitro = 30 # definir el tamaño del paso Numero de pie = 0,1 # realizar la búsqueda de descenso de gradiente mejor, puntaje = descenso de gradiente(objetivo, derivado, límites, nitro, Numero de pie) impresión(‘¡Hecho!’) impresión(‘f (% s) =% f’ % (mejor, puntaje)) |
La ejecución del ejemplo comienza con un punto aleatorio en el espacio de búsqueda y luego aplica el algoritmo de descenso de gradiente, informando el rendimiento a lo largo del camino.
Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o procedimiento de evaluación, o las diferencias en la precisión numérica. Considere ejecutar el ejemplo varias veces y compare el resultado promedio.
En este caso, podemos ver que el algoritmo encuentra una buena solución después de aproximadamente 20-30 iteraciones con una evaluación de función de aproximadamente 0.0. Tenga en cuenta que el óptimo para esta función está en f (0.0) = 0.0.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
> 0 f ([-0.36308639]) = 0,13183 > 1 f ([-0.29046911]) = 0.08437 > 2 f ([-0.23237529]) = 0.05400 > 3 f ([-0.18590023]) = 0.03456 > 4 f ([-0.14872018]) = 0.02212 > 5 f ([-0.11897615]) = 0.01416 > 6 f ([-0.09518092]) = 0,00906 > 7 f ([-0.07614473]) = 0,00580 > 8 f ([-0.06091579]) = 0,00371 > 9 f ([-0.04873263]) = 0,00237 > 10 f ([-0.0389861]) = 0,00152 > 11 f ([-0.03118888]) = 0,00097 > 12 f ([-0.02495111]) = 0,00062 > 13 f ([-0.01996089]) = 0,00040 > 14 f ([-0.01596871]) = 0,00025 > 15 f ([-0.01277497]) = 0,00016 > 16 f ([-0.01021997]) = 0,00010 > 17 f ([-0.00817598]) = 0,00007 > 18 f ([-0.00654078]) = 0,00004 > 19 f ([-0.00523263]) = 0,00003 > 20 f ([-0.0041861]) = 0,00002 > 21 f ([-0.00334888]) = 0,00001 > 22 f ([-0.0026791]) = 0,00001 > 23 f ([-0.00214328]) = 0,00000 > 24 f ([-0.00171463]) = 0,00000 > 25 f ([-0.0013717]) = 0,00000 > 26 f ([-0.00109736]) = 0,00000 > 27 f ([-0.00087789]) = 0,00000 > 28 f ([-0.00070231]) = 0,00000 > 29 f ([-0.00056185]) = 0,00000 ¡Hecho! F([-0.00056185]) = 0,000000 |
Ahora, permítanos sentir la importancia de un buen tamaño de paso.
Establezca el tamaño del paso en un valor grande, como 1.0, y vuelva a ejecutar la búsqueda.
|
... # definir el tamaño del paso Numero de pie = 1.0 |
Ejecute el ejemplo con el tamaño de paso más grande e inspeccione los resultados.
Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o procedimiento de evaluación, o las diferencias en la precisión numérica. Considere ejecutar el ejemplo varias veces y compare el resultado promedio.
Podemos ver que la búsqueda no encuentra los óptimos, sino que rebota alrededor del dominio, en este caso entre los valores 0,64820935 y -0,64820935.
|
… > 25 f ([0.64820935]) = 0.42018 > 26 f ([-0.64820935]) = 0.42018 > 27 f ([0.64820935]) = 0.42018 > 28 f ([-0.64820935]) = 0.42018 > 29 f ([0.64820935]) = 0.42018 ¡Hecho! F([0.64820935]) = 0,420175 |
Ahora, pruebe con un tamaño de paso mucho más pequeño, como 1e-8.
|
... # definir el tamaño del paso Numero de pie = 1e–5 |
Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o procedimiento de evaluación, o las diferencias en la precisión numérica. Considere ejecutar el ejemplo varias veces y compare el resultado promedio.
Al volver a ejecutar la búsqueda, podemos ver que el algoritmo se mueve muy lentamente por la pendiente de la función objetivo desde el punto de partida.
|
… > 25 f ([-0.87315153]) = 0,76239 > 26 f ([-0.87313407]) = 0,76236 > 27 f ([-0.8731166]) = 0,76233 > 28 f ([-0.87309914]) = 0,76230 > 29 f ([-0.87308168]) = 0,76227 ¡Hecho! F([-0.87308168]) = 0,762272 |
Estos dos ejemplos rápidos resaltan los problemas al seleccionar un tamaño de paso que es demasiado grande o demasiado pequeño y la importancia general de probar muchos valores de tamaño de paso diferentes para una función objetivo determinada.
Por último, podemos volver a cambiar la tasa de aprendizaje a 0,1 y visualizar el progreso de la búsqueda en un gráfico de la función objetivo.
Primero, podemos actualizar el descenso de gradiente() función para almacenar todas las soluciones y su puntuación encontradas durante la optimización como listas y devolverlas al final de la búsqueda en lugar de la mejor solución encontrada.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 |
# algoritmo de descenso de gradiente def descenso de gradiente(objetivo, derivado, límites, nitro, Numero de pie): # rastrear todas las soluciones soluciones, puntuaciones = lista(), lista() # generar un punto inicial solución = límites[[:, 0] + rand(len(límites)) * (límites[[:, 1] – límites[[:, 0]) # ejecutar el descenso de gradiente por I en distancia(nitro): # calcular gradiente degradado = derivado(solución) # Da un paso solución = solución – Numero de pie * degradado # evaluar el punto candidato solution_eval = objetivo(solución) # solución de tienda soluciones.adjuntar(solución) puntuaciones.adjuntar(solution_eval) # informe de progreso impresión(‘>% d f (% s) =% .5f’ % (I, solución, solution_eval)) regreso [[soluciones, puntuaciones] |
Se puede llamar a la función y podemos obtener las listas de las soluciones y sus puntuaciones encontradas durante la búsqueda.
|
... # realizar la búsqueda de descenso de gradiente soluciones, puntuaciones = descenso de gradiente(objetivo, derivado, límites, nitro, Numero de pie) |
Podemos crear una gráfica lineal de la función objetivo, como antes.
|
... # sample input range uniformly at 0.1 increments inputs = arange(bounds[[0,0], bounds[[0,1]+0.1, 0.1) # compute targets results = objective(inputs) # create a line plot of input vs result pyplot.plot(inputs, results) |
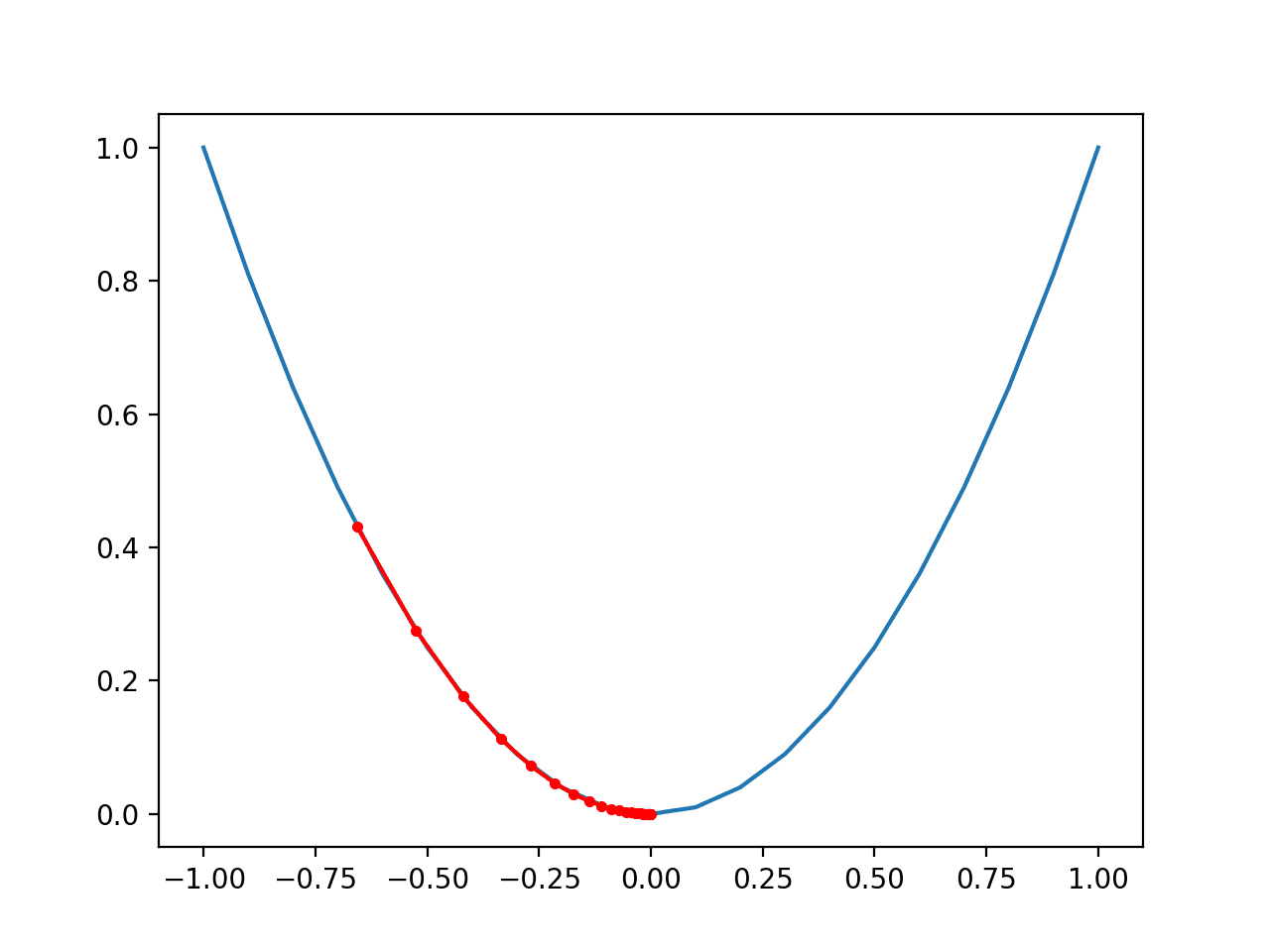
Finally, we can plot each solution found as a red dot and connect the dots with a line so we can see how the search moved downhill.
|
... # plot the solutions found pyplot.plot(solutions, scores, ‘.-‘, color=‘red’) |
Tying this all together, the complete example of plotting the result of the gradient descent search on the one-dimensional test function is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 |
# example of plotting a gradient descent search on a one-dimensional function de numpy import asarray de numpy import arange de numpy.random import rand de matplotlib import pyplot # objective function def objective(X): regreso x**2.0 # derivative of objective function def derivative(X): regreso x * 2.0 # gradient descent algorithm def gradient_descent(objective, derivative, bounds, n_iter, step_size): # track all solutions solutions, scores = list(), list() # generate an initial point solution = bounds[[:, 0] + rand(len(bounds)) * (bounds[[:, 1] – bounds[[:, 0]) # run the gradient descent for i in range(n_iter): # calculate gradient gradient = derivative(solution) # take a step solution = solution – step_size * gradient # evaluate candidate point solution_eval = objective(solution) # store solution solutions.append(solution) scores.append(solution_eval) # report progress print(‘>%d f(%s) = %.5f’ % (i, solution, solution_eval)) regreso [[solutions, scores] # define range for input bounds = asarray([[[[–1.0, 1.0]]) # define the total iterations n_iter = 30 # define the step size step_size = 0.1 # perform the gradient descent search solutions, scores = gradient_descent(objective, derivative, bounds, n_iter, step_size) # sample input range uniformly at 0.1 increments inputs = arange(bounds[[0,0], bounds[[0,1]+0.1, 0.1) # compute targets results = objective(inputs) # create a line plot of input vs result pyplot.plot(inputs, results) # plot the solutions found pyplot.plot(solutions, scores, ‘.-‘, color=‘red’) # show the plot pyplot.show() |
Running the example performs the gradient descent search on the objective function as before, except in this case, each point found during the search is plotted.
Nota: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, we can see that the search started about halfway up the left part of the function and stepped downhill to the bottom of the basin.
We can see that in the parts of the objective function with the larger curve, the derivative (gradient) is larger, and in turn, larger steps are taken. Similarly, the gradient is smaller as we get closer to the optima, and in turn, smaller steps are taken.
This highlights that the step size is used as a scale factor on the magnitude of the gradient (curvature) of the objective function.

Plot of the Progress of Gradient Descent on a One Dimensional Objective Function
Further Reading
This section provides more resources on the topic if you are looking to go deeper.
Books
APIs
Articles
Summary
In this tutorial, you discovered how to implement gradient descent optimization from scratch.
Specifically, you learned:
- Gradient descent is a general procedure for optimizing a differentiable objective function.
- How to implement the gradient descent algorithm from scratch in Python.
- How to apply the gradient descent algorithm to an objective function.
Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.
