Sobrecarga es una explicación común para el pobre desempeño de un modelo de predicción.
Un análisis de la dinámica de aprendizaje puede ayudar a identificar si un modelo ha superado el conjunto de datos de capacitación y puede sugerir una configuración alternativa para su uso que podría dar lugar a un mejor rendimiento predictivo.
Realizar un análisis de la dinámica de aprendizaje es sencillo para los algoritmos que aprenden de forma incremental, como las redes neuronales, pero está menos claro cómo podríamos realizar el mismo análisis con otros algoritmos que no aprenden de forma incremental, como los árboles de decisión, los vecinos más cercanos y otros algoritmos generales de la biblioteca de aprendizaje de la máquina Scikit-learn.
En este tutorial, descubrirá cómo identificar la sobrecarga de los modelos de aprendizaje de máquinas en Python.
Después de completar este tutorial, lo sabrás:
- El exceso de equipamiento es una posible causa de un pobre rendimiento de generalización de un modelo predictivo.
- La adaptación puede ser analizada para los modelos de aprendizaje de la máquina variando los hiperparámetros clave del modelo.
- Aunque la sobreadaptación es una herramienta útil para el análisis, no debe confundirse con la selección de modelos.
Empecemos.

Identificar los modelos de aprendizaje de la máquina de sobreajuste con Scikit-Learn
Foto de Bonnie Moreland, algunos derechos reservados.
Resumen del Tutorial
Este tutorial está dividido en cinco partes; son:
- ¿Qué es la sobrecarga
- Cómo realizar un análisis de sobreajuste
- Ejemplo de sobreajuste en Scikit-Learn
- Contra-ejemplo de la adaptación en Scikit-Learn
- Separar el análisis de la adaptación de la selección del modelo
¿Qué es la sobrecarga
El sobreajuste se refiere a un comportamiento no deseado de un algoritmo de aprendizaje de la máquina utilizado para el modelado predictivo.
Se da el caso de que el rendimiento del modelo en el conjunto de datos de entrenamiento se mejora a costa de un peor rendimiento en los datos no vistos durante el entrenamiento, como un conjunto de datos de prueba de retención o nuevos datos.
Podemos identificar si un modelo de aprendizaje de una máquina se ha sobreajustado evaluando primero el modelo en el conjunto de datos de entrenamiento y luego evaluando el mismo modelo en un conjunto de datos de prueba de retención.
Si el rendimiento del modelo en el conjunto de datos de entrenamiento es significativamente mejor que el rendimiento en el conjunto de datos de prueba, entonces el modelo puede haber superado el conjunto de datos de entrenamiento.
Nos preocupamos por el exceso de equipamiento porque es una causa común para «generalización deficiente«del modelo, medido por el alto»error de generalización.” Ese es un error del modelo al hacer predicciones sobre nuevos datos.
Esto significa que si nuestro modelo tiene un rendimiento pobre, tal vez sea porque tiene un exceso de equipamiento.
Pero, ¿qué significa si la actuación de una modelo es «significativamente mejor«en el set de entrenamiento comparado con el set de prueba?
Por ejemplo, es común y quizás normal que el modelo tenga un mejor rendimiento en el set de entrenamiento que en el set de prueba.
Como tal, podemos realizar un análisis del algoritmo en el conjunto de datos para exponer mejor el comportamiento de sobrecarga.
Cómo realizar un análisis de sobreajuste
Un análisis de adaptación es un enfoque para explorar cómo y cuándo un modelo específico se adapta a un conjunto de datos específico.
Es una herramienta que puede ayudarte a aprender más sobre la dinámica de aprendizaje de un modelo de aprendizaje de una máquina.
Esto podría lograrse revisando el comportamiento del modelo durante una sola ejecución para algoritmos como las redes neuronales que se ajustan al conjunto de datos de entrenamiento de forma incremental.
Se puede calcular un gráfico del rendimiento del modelo en el tren y el conjunto de pruebas en cada punto durante el entrenamiento y se pueden crear gráficos. Este gráfico se denomina a menudo gráfico de curva de aprendizaje, y muestra una curva para el rendimiento del modelo en el conjunto de entrenamiento y una curva para el conjunto de pruebas para cada incremento de aprendizaje.
Si desea saber más sobre las curvas de aprendizaje de los algoritmos que aprenden de forma incremental, consulte el tutorial:
El patrón común de sobreajuste puede verse en los gráficos de la curva de aprendizaje, en los que el rendimiento del modelo en el conjunto de datos de entrenamiento sigue mejorando (por ejemplo, la pérdida o el error sigue disminuyendo o la precisión sigue aumentando) y el rendimiento en el conjunto de pruebas o validación mejora hasta un punto y luego empieza a empeorar.
Si se observa este patrón, entonces el entrenamiento debe detenerse en el punto en que el rendimiento empeora en el conjunto de entrenamiento para los algoritmos que aprenden de forma incremental
Esto tiene sentido para los algoritmos que aprenden de forma incremental como las redes neuronales, pero ¿qué pasa con otros algoritmos?
- ¿Cómo se realiza un análisis de sobreajuste para los algoritmos de aprendizaje de máquina en scikit-learn?
Un enfoque para realizar un análisis de sobreajuste en algoritmos que no aprenden de forma incremental es variar un hiperparámetro clave del modelo y evaluar el rendimiento del modelo en el tren y los conjuntos de pruebas para cada configuración.
Para dejarlo claro, vamos a explorar un caso de análisis de un modelo para la adaptación en la siguiente sección.
Ejemplo de sobreajuste en Scikit-Learn
En esta sección, veremos un ejemplo de la adaptación de un modelo de aprendizaje de una máquina a un conjunto de datos de entrenamiento.
Primero, definamos un conjunto de datos de clasificación sintética.
Utilizaremos la función make_classification() para definir un problema de predicción de clasificación binaria (de dos clases) con 10.000 ejemplos (filas) y 20 características de entrada (columnas).
En el ejemplo que figura a continuación se crea el conjunto de datos y se resume la forma de los componentes de entrada y salida.
|
# Conjunto de datos de clasificación sintética de sklearn.conjuntos de datos importación hacer_clasificación # Definir el conjunto de datos X, y = make_classification(n_muestras=10000, n_funciones=20, n_informativo=5, n_redundante=15, estado_aleatorio=1) # resumir el conjunto de datos imprimir(X.forma, y.forma) |
Ejecutando el ejemplo se crea el conjunto de datos y se informa de la forma, confirmando nuestras expectativas.
A continuación, necesitamos dividir el conjunto de datos en subconjuntos de tren y de prueba.
Utilizaremos la función train_test_split() y dividiremos los datos en un 70 por ciento para entrenar un modelo y un 30 por ciento para evaluarlo.
|
# Dividir un conjunto de datos en trenes y conjuntos de pruebas de sklearn.conjuntos de datos importación make_classification de sklearn.model_selection importación prueba_de_trenes_split # Crear un conjunto de datos X, y = make_classification(n_muestras=10000, n_funciones=20, n_informativo=5, n_redundante=15, estado_aleatorio=1) # Dividido en conjuntos de prueba de trenes X_tren, X_test, y_tren, y_test = prueba_de_trenes_split(X, y, tamaño_de_prueba=0.3) # Resumir la forma del tren y los juegos de prueba imprimir(X_tren.forma, X_test.forma, y_tren.forma, y_test.forma) |
La ejecución del ejemplo divide el conjunto de datos y podemos confirmar que tenemos 70k ejemplos para el entrenamiento y 30k para la evaluación de un modelo.
|
(7000, 20) (3000, 20) (7000,) (3000,) |
A continuación, podemos explorar un modelo de aprendizaje de la máquina que sobrepase el conjunto de datos de entrenamiento.
Usaremos un árbol de decisión a través del Clasificador de Árbol de Decisión y probaremos diferentes profundidades de árbol con el «max_depth«argumento».
Los árboles de decisión poco profundos (por ejemplo, de pocos niveles) generalmente no se sobreponen, pero tienen un rendimiento deficiente (alto sesgo, baja varianza). Mientras que los árboles profundos (por ejemplo, muchos niveles) generalmente se sobreponen y tienen un buen rendimiento (bajo sesgo, alta varianza). Un árbol deseable es aquel que no es tan superficial como para tener poca habilidad y no es tan profundo como para sobreajustar el conjunto de datos de entrenamiento.
Evaluamos las profundidades de los árboles de decisión de 1 a 20.
|
... # Definir las profundidades de los árboles para evaluar valores = [[i para i en rango(1, 21)] |
Enumeraremos cada profundidad de árbol, ajustaremos un árbol con una profundidad dada en el conjunto de datos de entrenamiento, y luego evaluaremos el árbol tanto en el tren como en los conjuntos de pruebas.
La expectativa es que a medida que la profundidad del árbol aumente, el rendimiento en el entrenamiento y las pruebas mejorará hasta cierto punto, y a medida que el árbol se haga demasiado profundo, comenzará a superar el conjunto de datos de entrenamiento a expensas de un peor rendimiento en el conjunto de pruebas de retención.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
... # Evaluar un árbol de decisión para cada profundidad para i en valores: # Configurar el modelo modelo = DecisionTreeClassifier(max_depth=i) # Modelo de ajuste en el conjunto de datos de entrenamiento modelo.encajar(X_tren, y_tren) # Evaluar en el conjunto de datos del tren train_yhat = modelo.predecir(X_tren) train_acc = accuracy_score(y_tren, train_yhat) puntajes del tren.anexar(train_acc) # Evaluar en el conjunto de datos de la prueba test_yhat = modelo.predecir(X_test) test_acc = accuracy_score(y_test, test_yhat) test_scores.anexar(test_acc) # Resumir el progreso… imprimir(«>%d, tren: %.3f, prueba: %.3f % (i, train_acc, test_acc)) |
Al final de la carrera, trazaremos todos los resultados de la precisión del modelo en el tren y los juegos de prueba para la comparación visual.
|
... # Gráfica de puntajes de trenes y pruebas contra la profundidad de los árboles pyplot.parcela(valores, puntajes del tren, ‘-o’, etiqueta=«Tren) pyplot.parcela(valores, test_scores, ‘-o’, etiqueta=«Prueba) pyplot.leyenda() pyplot.mostrar() |
Enlazando esto, el ejemplo completo de la exploración de diferentes profundidades de árboles en el conjunto de datos de la clasificación binaria sintética se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
# Evaluar el rendimiento del árbol de decisiones en el tren y probar conjuntos con diferentes profundidades de árbol de sklearn.conjuntos de datos importación make_classification de sklearn.model_selection importación prueba_de_trenes_split de sklearn.métrica importación accuracy_score de sklearn.árbol importación DecisionTreeClassifier de matplotlib importación pyplot # Crear un conjunto de datos X, y = make_classification(n_muestras=10000, n_funciones=20, n_informativo=5, n_redundante=15, estado_aleatorio=1) # Dividido en conjuntos de prueba de trenes X_tren, X_test, y_tren, y_test = prueba_de_trenes_split(X, y, tamaño_de_prueba=0.3) # Definir listas para recoger las puntuaciones puntajes del tren, test_scores = lista(), lista() # Definir las profundidades de los árboles para evaluar valores = [[i para i en rango(1, 21)] # Evaluar un árbol de decisión para cada profundidad para i en valores: # Configurar el modelo modelo = DecisionTreeClassifier(max_depth=i) # Modelo de ajuste en el conjunto de datos de entrenamiento modelo.encajar(X_tren, y_tren) # Evaluar en el conjunto de datos del tren train_yhat = modelo.predecir(X_tren) train_acc = accuracy_score(y_tren, train_yhat) puntajes del tren.anexar(train_acc) # Evaluar en el conjunto de datos de la prueba test_yhat = modelo.predecir(X_test) test_acc = accuracy_score(y_test, test_yhat) test_scores.anexar(test_acc) # Resumir el progreso… imprimir(«>%d, tren: %.3f, prueba: %.3f % (i, train_acc, test_acc)) # Gráfica de puntajes de trenes y pruebas contra la profundidad de los árboles pyplot.parcela(valores, puntajes del tren, ‘-o’, etiqueta=«Tren) pyplot.parcela(valores, test_scores, ‘-o’, etiqueta=«Prueba) pyplot.leyenda() pyplot.mostrar() |
Al ejecutar el ejemplo se ajusta y evalúa un árbol de decisión en el tren y conjuntos de pruebas para cada profundidad del árbol y se informa de los resultados de la precisión.
Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o el procedimiento de evaluación, o las diferencias en la precisión numérica. Considere ejecutar el ejemplo unas cuantas veces y compare el resultado promedio.
En este caso, podemos ver una tendencia a aumentar la precisión del conjunto de datos de entrenamiento con la profundidad del árbol hasta un punto alrededor de una profundidad de 19-20 niveles donde el árbol encaja perfectamente en el conjunto de datos de entrenamiento.
También podemos ver que la precisión del equipo de prueba mejora con la profundidad de los árboles hasta una profundidad de unos ocho o nueve niveles, después de lo cual la precisión comienza a empeorar con cada aumento de la profundidad de los árboles.
Esto es exactamente lo que esperaríamos ver en un patrón de sobreajuste.
Elegiríamos una profundidad de ocho o nueve árboles antes de que el modelo empiece a sobrecargar el conjunto de datos de entrenamiento.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
>1, tren: 0.769, prueba: 0.761 >2, tren: 0.808, prueba: 0.804 >3, tren: 0.879, prueba: 0.878 >4, tren: 0.902, prueba: 0.896 >5, tren: 0.915, prueba: 0.903 >6, tren: 0.929, prueba: 0.918 >7, tren: 0.942, prueba: 0.921 >8, tren: 0.951, prueba: 0.924 >9, tren: 0.959, prueba: 0.926 >10, tren: 0.968, prueba: 0.923 >11, tren: 0.977, prueba: 0.925 >12, tren: 0.983, prueba: 0.925 >13, tren: 0.987, prueba: 0.926 >14, tren: 0.992, prueba: 0.921 >15, tren: 0.995, prueba: 0.920 >16, tren: 0.997, prueba: 0.913 >17, tren: 0.999, prueba: 0.918 >18, tren: 0.999, prueba: 0.918 >19, tren: 1.000, prueba: 0.914 >20, tren: 1.000, prueba: 0.913 |
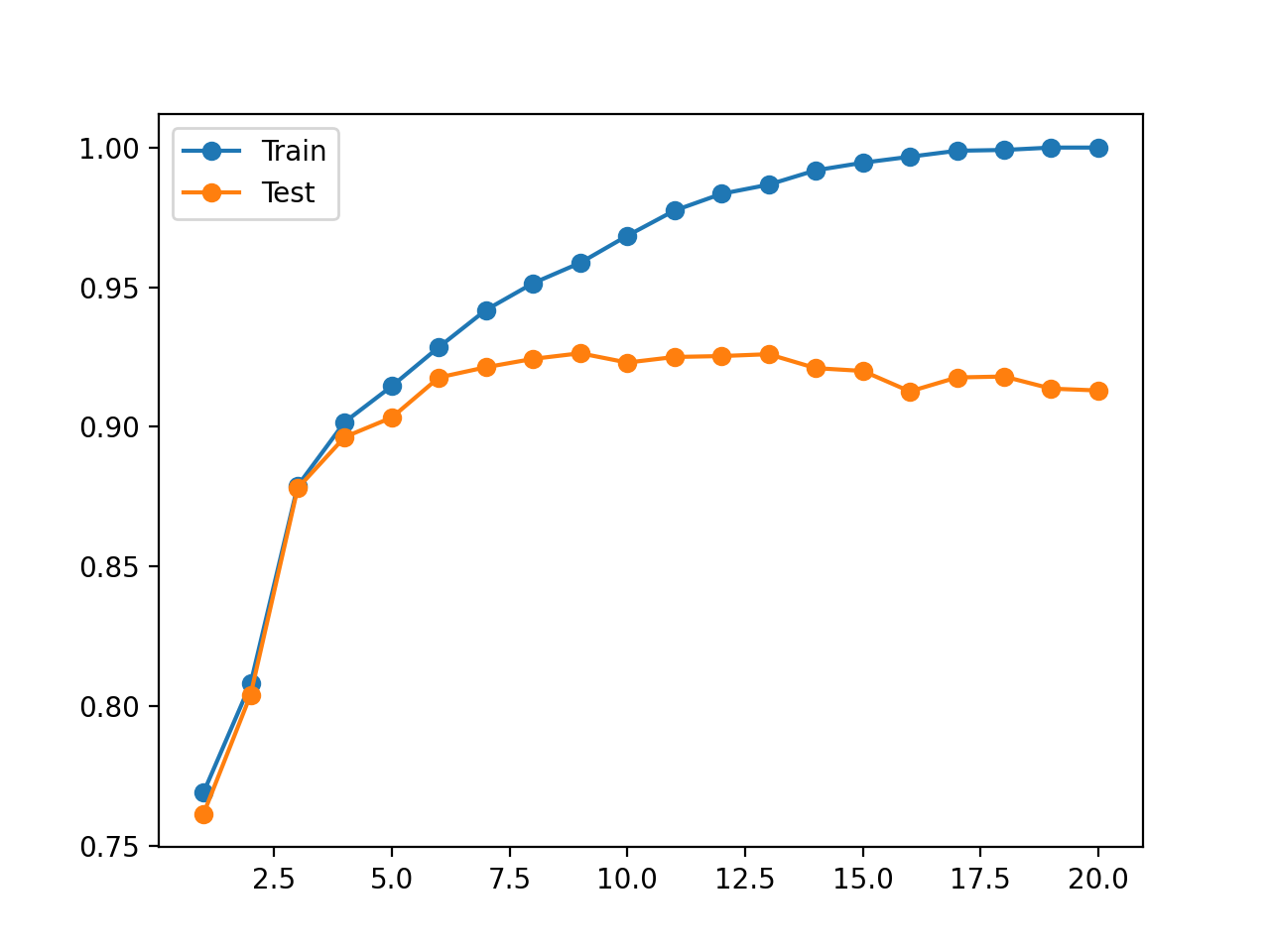
También se crea una figura que muestra gráficos lineales de la precisión del modelo en el tren y conjuntos de prueba con diferentes profundidades de árboles.
El gráfico muestra claramente que el aumento de la profundidad de los árboles en las primeras etapas resulta en una mejora correspondiente tanto en el tren como en los conjuntos de prueba.
Esto continúa hasta una profundidad de alrededor de 10 niveles, después de lo cual se muestra que el modelo se sobrepone al conjunto de datos de entrenamiento a costa de un peor rendimiento en el conjunto de datos de retención.

Trazado de líneas de precisión del árbol de decisión en el tren y conjuntos de datos de prueba para diferentes profundidades de árbol
Este análisis es interesante. Muestra por qué el modelo tiene un peor desempeño en el conjunto de pruebas de retención cuando…max_depth» se establece en grandes valores.
Pero no es necesario.
Podemos elegir fácilmente un «max_depth«utilizando una búsqueda de cuadrícula sin realizar un análisis de por qué algunos valores resultan en un mejor rendimiento y otros en un peor rendimiento.
De hecho, en la siguiente sección, mostraremos dónde este análisis puede ser engañoso.
Contra-ejemplo de la adaptación en Scikit-Learn
A veces, podemos realizar un análisis del comportamiento del modelo de aprendizaje de la máquina y ser engañados por los resultados.
Un buen ejemplo de esto es variar el número de vecinos para los algoritmos de vecinos más cercanos, que podemos implementar usando la clase KNeighborsClassifier y configurar a través de la clase «n_vecinos«argumento».
Olvidemos cómo funciona KNN por el momento.
Podemos realizar el mismo análisis del algoritmo KNN que hicimos en la sección anterior para el árbol de decisión y ver si nuestro modelo se ajusta a diferentes valores de configuración. En este caso, variaremos el número de vecinos de 1 a 50 para obtener más del efecto.
El ejemplo completo figura a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
# Evaluar el rendimiento de los knn en el tren y probar conjuntos con diferentes números de vecinos de sklearn.conjuntos de datos importación make_classification de sklearn.model_selection importación prueba_de_trenes_split de sklearn.métrica importación accuracy_score de sklearn.vecinos importación KNeighborsClassifier de matplotlib importación pyplot # Crear un conjunto de datos X, y = make_classification(n_muestras=10000, n_funciones=20, n_informativo=5, n_redundante=15, estado_aleatorio=1) # Dividido en conjuntos de prueba de trenes X_tren, X_test, y_tren, y_test = prueba_de_trenes_split(X, y, tamaño_de_prueba=0.3) # Definir listas para recoger las puntuaciones puntajes del tren, test_scores = lista(), lista() # Definir las profundidades de los árboles para evaluar valores = [[i para i en rango(1, 51)] # Evaluar un árbol de decisión para cada profundidad para i en valores: # Configurar el modelo modelo = KNeighborsClassifier(n_vecinos=i) # Modelo de ajuste en el conjunto de datos de entrenamiento modelo.encajar(X_tren, y_tren) # Evaluar en el conjunto de datos del tren train_yhat = modelo.predecir(X_tren) train_acc = accuracy_score(y_tren, train_yhat) puntajes del tren.anexar(train_acc) # Evaluar en el conjunto de datos de la prueba test_yhat = modelo.predecir(X_test) test_acc = accuracy_score(y_test, test_yhat) test_scores.anexar(test_acc) # Resumir el progreso… imprimir(«>%d, tren: %.3f, prueba: %.3f % (i, train_acc, test_acc)) # Trama del tren y resultados de la prueba vs número de vecinos pyplot.parcela(valores, puntajes del tren, ‘-o’, etiqueta=«Tren) pyplot.parcela(valores, test_scores, ‘-o’, etiqueta=«Prueba) pyplot.leyenda() pyplot.mostrar() |
Ejecutando el ejemplo se ajusta y evalúa un modelo KNN en el tren y conjuntos de pruebas para cada número de vecinos y reporta los resultados de precisión.
Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o el procedimiento de evaluación, o las diferencias en la precisión numérica. Considere ejecutar el ejemplo unas cuantas veces y compare el resultado promedio.
Recordemos que buscamos un patrón en el que el rendimiento en el conjunto de pruebas mejora y luego comienza a empeorar, y el rendimiento en el conjunto de entrenamiento sigue mejorando.
No vemos este patrón.
En cambio, vemos que la precisión en el conjunto de datos de entrenamiento comienza con una precisión perfecta y disminuye con casi cada aumento en el número de vecinos.
También vemos que el rendimiento del modelo en la prueba de retención mejora hasta un valor de unos cinco vecinos, se mantiene nivelado y comienza una tendencia descendente después de eso.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 |
>1, tren: 1.000, prueba: 0.919 >2, tren: 0.965, prueba: 0.916 >3, tren: 0.962, prueba: 0.932 >4, tren: 0.957, prueba: 0.932 >5, tren: 0.954, prueba: 0.935 >6, tren: 0.953, prueba: 0.934 >7, tren: 0.952, prueba: 0.932 >8, tren: 0.951, prueba: 0.933 >9, tren: 0.949, prueba: 0.933 >10, tren: 0.950, prueba: 0.935 >11, tren: 0.947, prueba: 0.934 >12, tren: 0.947, prueba: 0.933 >13, tren: 0.945, prueba: 0.932 >14, tren: 0.945, prueba: 0.932 >15, tren: 0.944, prueba: 0.932 >16, tren: 0.944, prueba: 0.934 >17, tren: 0.943, prueba: 0.932 >18, tren: 0.943, prueba: 0.935 >19, tren: 0.942, prueba: 0.933 >20, tren: 0.943, prueba: 0.935 >21, tren: 0.942, prueba: 0.933 >22, tren: 0.943, prueba: 0.933 >23, tren: 0.941, prueba: 0.932 >24, tren: 0.942, prueba: 0.932 >25, tren: 0.942, prueba: 0.931 >26, tren: 0.941, prueba: 0.930 >27, tren: 0.941, prueba: 0.932 >28, tren: 0.939, prueba: 0.932 >29, tren: 0.938, prueba: 0.931 >30, tren: 0.938, prueba: 0.931 >31, tren: 0.937, prueba: 0.931 >32, tren: 0.938, prueba: 0.931 >33, tren: 0.937, prueba: 0.930 >34, tren: 0.938, prueba: 0.931 >35, tren: 0.937, prueba: 0.930 >36, tren: 0.937, prueba: 0.928 >37, tren: 0.936, prueba: 0.930 >38, tren: 0.937, prueba: 0.930 >39, tren: 0.935, prueba: 0.929 >40, tren: 0.936, prueba: 0.929 >41, tren: 0.936, prueba: 0.928 >42, tren: 0.936, prueba: 0.929 >43, tren: 0.936, prueba: 0.930 >44, tren: 0.935, prueba: 0.929 >45, tren: 0.935, prueba: 0.929 >46, tren: 0.934, prueba: 0.929 >47, tren: 0.935, prueba: 0.929 >48, tren: 0.934, prueba: 0.929 >49, tren: 0.934, prueba: 0.929 >50, tren: 0.934, prueba: 0.929 |
También se crea una figura que muestra gráficos lineales de la precisión del modelo en el tren y conjuntos de prueba con diferentes números de vecinos.
Las tramas aclaran la situación. Parece que el gráfico de líneas para el conjunto de entrenamiento está cayendo para converger con la línea para el conjunto de prueba. De hecho, esto es exactamente lo que está sucediendo.
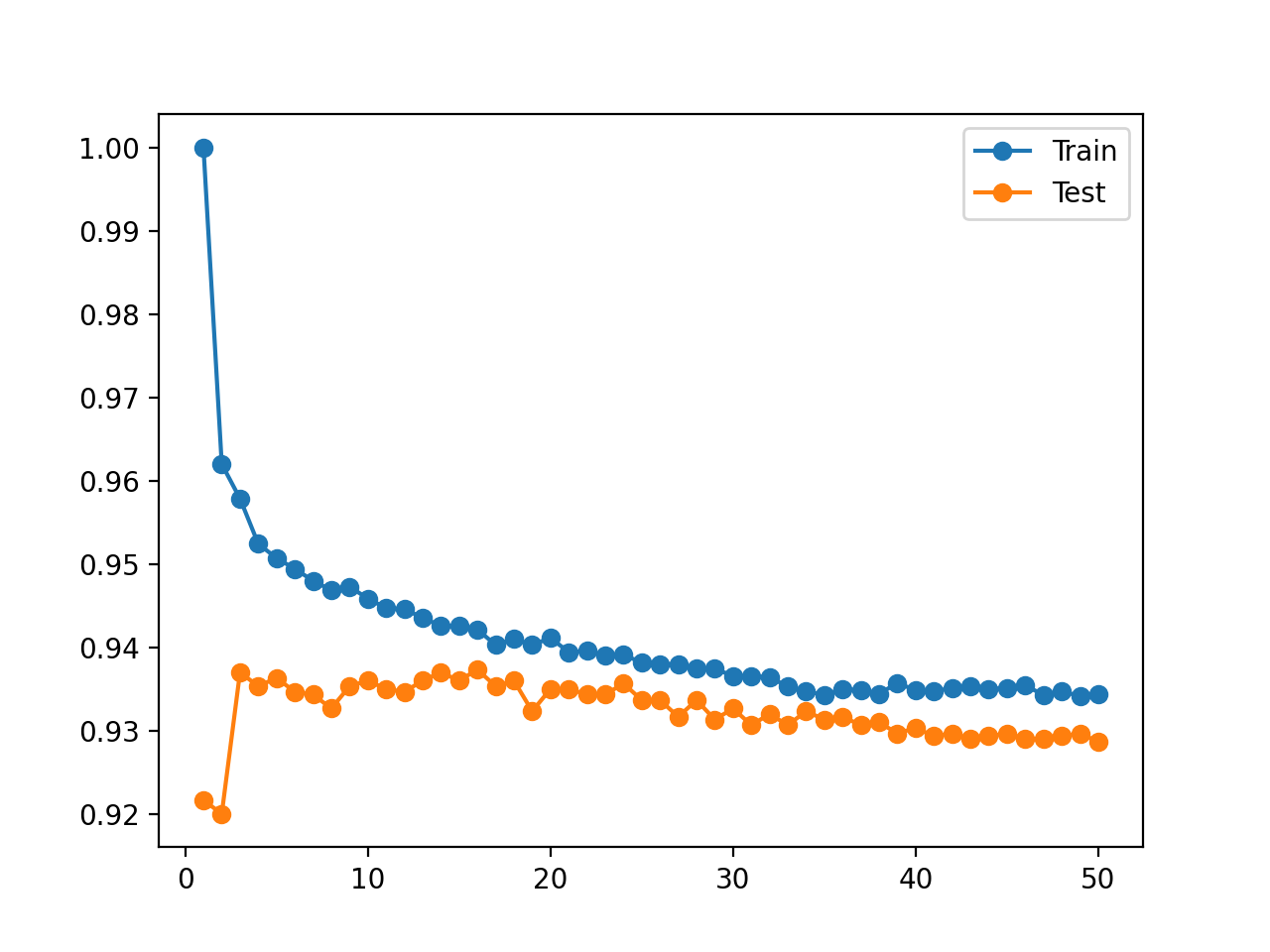
Trazado de la línea de precisión de KNN en el tren y los datos de prueba para diferentes números de vecinos
Ahora, recuerda cómo funciona KNN.
El «modelo» es en realidad todo el conjunto de datos de entrenamiento almacenados en una estructura de datos eficiente. La habilidad para el «modelo«en el conjunto de datos de entrenamiento debe ser del 100 por ciento y cualquier otra cosa es imperdonable.
De hecho, este argumento es válido para cualquier algoritmo de aprendizaje de máquina y corta hasta la médula la confusión en torno a la sobrecarga para los principiantes.
Separar el análisis de la adaptación de la selección del modelo
El exceso de equipamiento puede ser una explicación para el pobre desempeño de un modelo predictivo.
La creación de gráficos de curvas de aprendizaje que muestren la dinámica de aprendizaje de un modelo en el tren y el conjunto de datos de prueba es un análisis útil para aprender más sobre un modelo en un conjunto de datos.
Pero el overfitting no debe confundirse con la selección de modelos.
Elegimos un modelo predictivo o una configuración de modelo basada en su rendimiento fuera de muestra. Es decir, su rendimiento sobre nuevos datos no vistos durante el entrenamiento.
La razón por la que hacemos esto es que en el modelado predictivo, estamos interesados principalmente en un modelo que haga predicciones hábiles. Queremos el modelo que pueda hacer las mejores predicciones posibles dado el tiempo y los recursos computacionales que tenemos disponibles.
Esto podría significar que elegimos un modelo que parece que ha superado el conjunto de datos de entrenamiento. En cuyo caso, un análisis de sobreajuste podría ser engañoso.
También podría significar que el modelo tiene un rendimiento pobre o terrible en el conjunto de datos de entrenamiento.
En general, si nos preocupamos por el rendimiento del modelo en el conjunto de datos de entrenamiento en la selección del modelo, entonces esperamos que un modelo tenga un rendimiento perfecto en el conjunto de datos de entrenamiento. Son datos que tenemos disponibles; no deberíamos tolerar nada menos.
Como vimos con el ejemplo de KNN arriba, podemos lograr un rendimiento perfecto en el conjunto de entrenamiento almacenando el conjunto de entrenamiento directamente y devolviendo las predicciones con un vecino a costa de un rendimiento pobre en cualquier dato nuevo.
- ¿No sería mejor un modelo que funcione bien tanto en el tren como en los datos de prueba?
Tal vez. Pero, tal vez no.
Este argumento se basa en la idea de que un modelo que funciona bien tanto en el tren como en las pruebas tiene una mejor comprensión del problema subyacente.
El corolario es que un modelo que tiene un buen rendimiento en el conjunto de pruebas pero que es malo en el conjunto de entrenamiento es afortunado (por ejemplo, una casualidad estadística) y un modelo que tiene un buen rendimiento en el conjunto de trenes pero que es malo en el conjunto de pruebas es un exceso de equipamiento.
Creo que este es el punto de fricción para los principiantes que a menudo preguntan cómo arreglar el equipamiento para su modelo de aprendizaje de la máquina de ciencias.
La preocupación es que un modelo debe funcionar bien tanto en el tren como en las pruebas, de lo contrario, están en problemas.
No es así..
El rendimiento del equipo de entrenamiento no es relevante durante la selección del modelo. Debe concentrarse en el rendimiento fuera de la muestra sólo cuando elija un modelo predictivo.
Más lecturas
Esta sección proporciona más recursos sobre el tema si desea profundizar en él.
Tutoriales
APIs
Artículos
Resumen
En este tutorial, descubriste cómo identificar la adaptación de los modelos de aprendizaje de máquinas en Python.
Específicamente, aprendiste:
- El exceso de equipamiento es una posible causa de un pobre rendimiento de generalización de un modelo predictivo.
- La adaptación puede ser analizada para los modelos de aprendizaje de la máquina variando los hiperparámetros clave del modelo.
- Aunque la sobreadaptación es una herramienta útil para el análisis, no debe confundirse con la selección de modelos.
¿Tiene alguna pregunta?
Haga sus preguntas en los comentarios de abajo y haré lo posible por responder.

