Muchos modelos de aprendizaje de máquinas funcionan mejor cuando las variables de entrada se transforman o escalan cuidadosamente antes del modelado.
Es conveniente, y por lo tanto común, aplicar las mismas transformaciones de datos, como la normalización y la estandarización, por igual a todas las variables de entrada. Esto puede lograr buenos resultados en muchos problemas. No obstante, se pueden obtener mejores resultados si se aplica cuidadosamente seleccionando qué datos se transforman para aplicarlos a cada variable de entrada antes del modelado.
En este tutorial, descubrirá cómo aplicar el escalado selectivo de las variables de entrada numérica.
Después de completar este tutorial, lo sabrás:
- Cómo cargar y calcular una línea base de rendimiento predictivo para el conjunto de datos de clasificación de la diabetes.
- Cómo evaluar la modelización de tuberías con transformaciones de datos aplicadas a ciegas a todas las variables de entrada numéricas.
- Cómo evaluar la modelización de tuberías con normalización y estandarización selectivas aplicadas a subconjuntos de variables de entrada.
Descubre la limpieza de datos, la selección de características, la transformación de datos, la reducción de la dimensionalidad y mucho más en mi nuevo libro, con 30 tutoriales paso a paso y el código fuente completo en Python.
Empecemos.

Cómo escalar selectivamente las variables de entrada numérica para el aprendizaje automático
Resumen del Tutorial
Este tutorial está dividido en tres partes; son:
- Conjunto de datos numéricos sobre la diabetes
- Escalado no selectivo de los insumos numéricos
- Normalizar todas las variables de entrada
- Estandarizar todas las variables de entrada
- Escalado selectivo de los insumos numéricos
- Normalizar sólo las variables de entrada no gausianas
- Estandarizar sólo las variables de entrada de tipo gaussiano
- Normalizar y estandarizar selectivamente las variables de entrada
Conjunto de datos numéricos sobre la diabetes
Como base de este tutorial, utilizaremos el llamado conjunto de datos de «diabetes» que ha sido ampliamente estudiado como un conjunto de datos de aprendizaje automático desde la década de 1990.
El conjunto de datos clasifica los datos de los pacientes como un inicio de diabetes dentro de cinco años o no. Hay 768 ejemplos y ocho variables de entrada. Es un problema de clasificación binaria.
Puedes aprender más sobre el conjunto de datos aquí:
No es necesario descargar el conjunto de datos; lo descargaremos automáticamente como parte de los ejemplos trabajados que siguen.
Mirando los datos, podemos ver que las nueve variables de entrada son numéricas.
|
6,148,72,35,0,33.6,0.627,50,1 1,85,66,29,0,26.6,0.351,31,0 8,183,64,0,0,23.3,0.672,32,1 1,89,66,23,94,28.1,0.167,21,0 0,137,40,35,168,43.1,2.288,33,1 … |
Podemos cargar este conjunto de datos en la memoria usando la biblioteca de Pandas.
El siguiente ejemplo descarga y resume el conjunto de datos sobre la diabetes.
|
# Cargar y resumir el conjunto de datos de la diabetes de pandas importación read_csv de pandas.trazando importación scatter_matrix de matplotlib importación pyplot # Cargar conjunto de datos url = «https://raw.githubusercontent.com/jbrownlee/Datasets/master/pima-indians-diabetes.csv» dataset = read_csv(url, encabezado=Ninguno) # resumir la forma del conjunto de datos imprimir(dataset.forma) # Histogramas de las variables dataset.hist() pyplot.mostrar() |
Ejecutando el ejemplo primero descarga el conjunto de datos y lo carga como un DataFrame.
Se imprime la forma del conjunto de datos, confirmando el número de filas, y nueve variables, ocho de entrada y un objetivo.
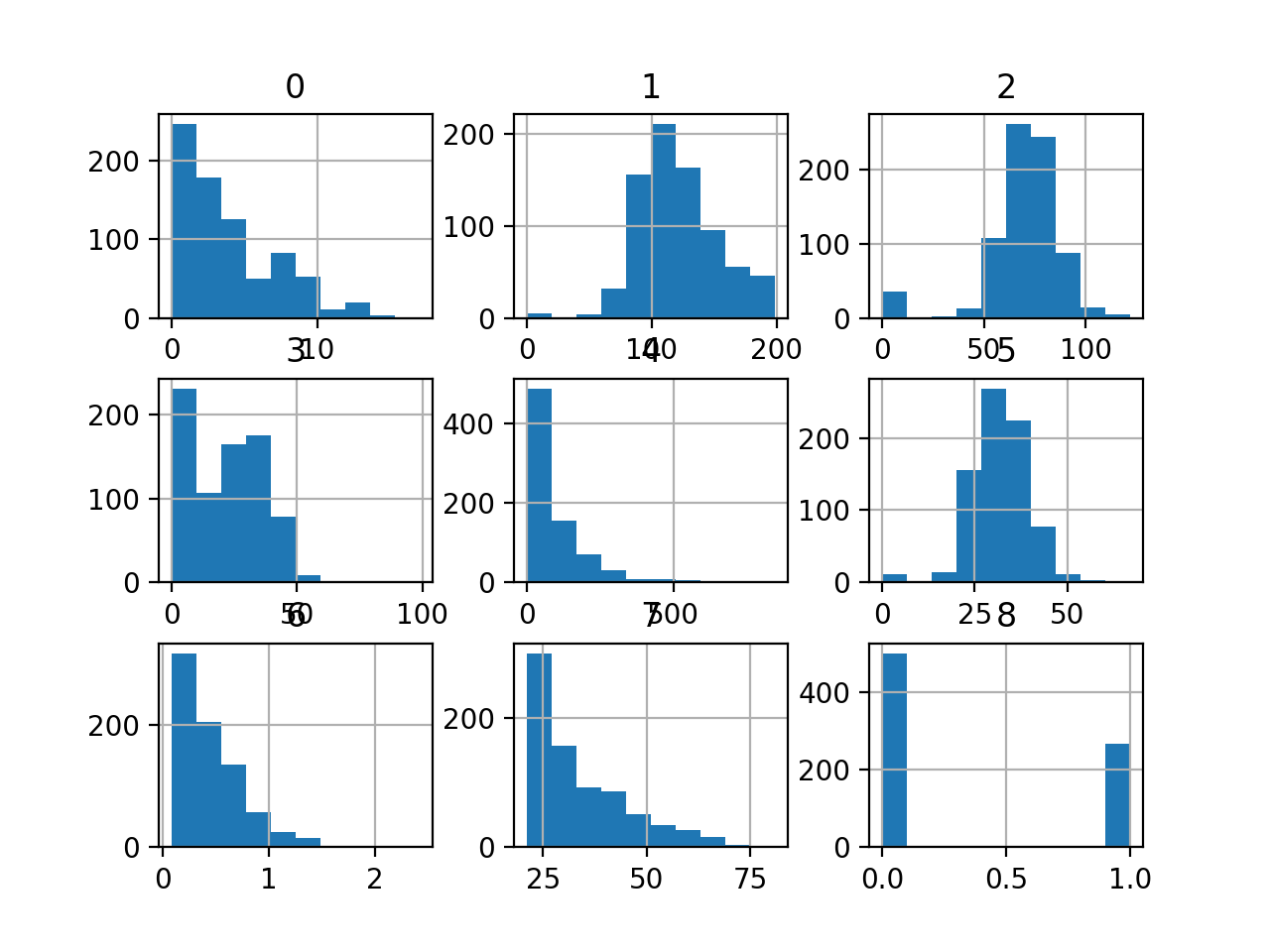
Finalmente, se crea un gráfico que muestra un histograma para cada variable del conjunto de datos.
Esto es útil, ya que podemos ver que algunas variables tienen una distribución de tipo gaussiano o gaussiano (1, 2, 5) y otras tienen una distribución de tipo exponencial (0, 3, 4, 6, 7). Esto puede sugerir la necesidad de diferentes transformaciones de datos numéricos para los diferentes tipos de variables de entrada.

Histograma de cada variable en el conjunto de datos de la clasificación de la diabetes
Ahora que estamos un poco familiarizados con el conjunto de datos, intentemos ajustar y evaluar un modelo en el conjunto de datos en bruto.
Utilizaremos un modelo de regresión logística ya que son un modelo lineal robusto y efectivo para las tareas de clasificación binaria. Evaluaremos el modelo usando la validación cruzada estratificada repetida k, una mejor práctica, y usaremos 10 pliegues y tres repeticiones.
El ejemplo completo figura a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
# Evaluar un modelo de regresión logística en el conjunto de datos brutos de la diabetes de numpy importación significa de numpy importación std de pandas importación read_csv de sklearn.preprocesamiento importación LabelEncoder de sklearn.model_selection importación puntaje_valor_cruzado de sklearn.model_selection importación RepeatedStratifiedKFold de sklearn.modelo_lineal importación LogisticRegression # Cargar conjunto de datos url = ‘https://raw.githubusercontent.com/jbrownlee/Datasets/master/pima-indians-diabetes.csv’ dataframe = read_csv(url, encabezado=Ninguno) datos = dataframe.valores # Separados en elementos de entrada y salida X, y = datos[[:, :–1], datos[[:, –1] # Preparar mínimamente el conjunto de datos X = X.astype(«flotar) y = LabelEncoder().fit_transform(y.astype(«str)) # Definir el modelo modelo = LogisticRegression(solver=«Liberal»…) # Definir el procedimiento de evaluación cv = RepeatedStratifiedKFold(n_splits=10, n_repeticiones=3, estado_aleatorio=1) # Evaluar el modelo m_scores = puntaje_valor_cruzado(modelo, X, y, puntuación=«exactitud, cv=cv, n_jobs=–1) # resumir el resultado imprimir(«Precisión: %.3f (%.3f) % (significa(m_scores), std(m_scores))) |
La ejecución del ejemplo evalúa el modelo e informa de la precisión de la media y la desviación estándar para ajustar un modelo de regresión logística en el conjunto de datos en bruto.
Sus resultados específicos pueden diferir dada la naturaleza estocástica del algoritmo de aprendizaje, la naturaleza estocástica del procedimiento de evaluación y las diferencias de precisión entre las máquinas y las versiones de las bibliotecas. Intente ejecutar el ejemplo unas cuantas veces.
En este caso, podemos ver que el modelo alcanzó una precisión de alrededor del 76,8 por ciento.
Ahora que hemos establecido una línea de base en el rendimiento del conjunto de datos, veamos si podemos mejorar el rendimiento utilizando el escalado de datos.
¿Quieres empezar a preparar los datos?
Toma mi curso intensivo gratuito de 7 días por correo electrónico ahora (con código de muestra).
Haga clic para inscribirse y también para obtener una versión gratuita del curso en formato PDF.
Descargue su minicurso GRATUITO
Escalado no selectivo de los insumos numéricos
Muchos algoritmos prefieren o requieren que las variables de entrada se escalen a un rango consistente antes de ajustar un modelo.
Esto incluye el modelo de regresión logística que supone que las variables de entrada tienen una distribución de probabilidad gaussiana. También puede proporcionar un modelo más estable numéricamente si las variables de entrada están estandarizadas. No obstante, incluso cuando se violan esas expectativas, la regresión logística puede funcionar bien o mejor para un conjunto de datos determinado, como puede ser el caso del conjunto de datos sobre la diabetes.
Dos técnicas comunes para escalar las variables de entrada numérica son la normalización y la estandarización.
La normalización escala cada variable de entrada al rango 0-1 y puede ser implementada usando la clase MinMaxScaler en scikit-learn. La normalización escala cada variable de entrada para tener una media de 0,0 y una desviación estándar de 1,0 y puede implementarse usando la clase StandardScaler en scikit-learn.
Para obtener más información sobre la normalización, la estandarización y cómo utilizar estos métodos en el aprendizaje científico, consulte el tutorial:
Un enfoque ingenuo del escalamiento de datos aplica una sola transformación a todas las variables de entrada, independientemente de su escala o distribución de probabilidad. Y esto es a menudo efectivo.
Intentemos normalizar y estandarizar todas las variables de entrada directamente y comparemos el rendimiento con el ajuste del modelo de regresión logística de la línea de base en los datos en bruto.
Normalizar todas las variables de entrada
Podemos actualizar el ejemplo de código de base para utilizar un conducto de modelado donde el primer paso es aplicar un escalador y el paso final es ajustar el modelo.
Esto garantiza que la operación de escalado se ajuste o prepare sólo en el conjunto de entrenamiento y luego se aplique al tren y a los conjuntos de pruebas durante el proceso de validación cruzada, evitando la fuga de datos. La fuga de datos puede dar lugar a una estimación optimista del rendimiento del modelo.
Esto puede lograrse utilizando la clase Pipeline, en la que cada paso de la tubería se define como una tupla con un nombre y la instancia de la transformación o modelo a utilizar.
|
... # Definir la tubería de modelación scaler = MinMaxScaler() modelo = LogisticRegression(solver=«Liberal»…) tubería = Oleoducto([[(‘s’,scaler),(‘m’,modelo)]) |
Enlazando todo esto, a continuación se enumera el ejemplo completo de la evaluación de una regresión logística en un conjunto de datos sobre la diabetes con todas las variables de entrada normalizadas.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
# Evaluar un modelo de regresión logística en el conjunto de datos normalizados de la diabetes de numpy importación significa de numpy importación std de pandas importación read_csv de sklearn.preprocesamiento importación LabelEncoder de sklearn.model_selection importación puntaje_valor_cruzado de sklearn.model_selection importación RepeatedStratifiedKFold de sklearn.tubería importación Oleoducto de sklearn.modelo_lineal importación LogisticRegression de sklearn.preprocesamiento importación MinMaxScaler # Cargar conjunto de datos url = ‘https://raw.githubusercontent.com/jbrownlee/Datasets/master/pima-indians-diabetes.csv’ dataframe = read_csv(url, encabezado=Ninguno) datos = dataframe.valores # Separados en elementos de entrada y salida X, y = datos[[:, :–1], datos[[:, –1] # Preparar mínimamente el conjunto de datos X = X.astype(«flotar) y = LabelEncoder().fit_transform(y.astype(«str)) # Definir la tubería de modelación modelo = LogisticRegression(solver=«Liberal»…) scaler = MinMaxScaler() tubería = Oleoducto([[(‘s’,scaler),(‘m’,modelo)]) # Definir el procedimiento de evaluación cv = RepeatedStratifiedKFold(n_splits=10, n_repeticiones=3, estado_aleatorio=1) # Evaluar el modelo m_scores = puntaje_valor_cruzado(tubería, X, y, puntuación=«exactitud, cv=cv, n_jobs=–1) # resumir el resultado imprimir(«Precisión: %.3f (%.3f) % (significa(m_scores), std(m_scores))) |
Al ejecutar el ejemplo se evalúa la tubería de modelación y se informa de la precisión de la media y la desviación estándar para ajustar un modelo de regresión logística en el conjunto de datos normalizados.
Sus resultados específicos pueden diferir dada la naturaleza estocástica del algoritmo de aprendizaje, la naturaleza estocástica del procedimiento de evaluación y las diferencias de precisión entre las máquinas y las versiones de las bibliotecas. Intente ejecutar el ejemplo unas cuantas veces.
En este caso, podemos ver que la normalización de las variables de entrada ha dado lugar a una disminución de la precisión de la clasificación media del 76,8% con un ajuste del modelo en los datos brutos a alrededor del 76,4% para el oleoducto con normalización.
A continuación, intentemos estandarizar todas las variables de entrada.
Estandarizar todas las variables de entrada
Podemos actualizar la tubería de modelación para usar la estandarización en lugar de la normalización para todas las variables de entrada antes de ajustar y evaluar el modelo de regresión logística.
Esta podría ser una transformación apropiada para aquellas variables de entrada con una distribución similar a la de Gauss, pero quizás no para las otras variables.
|
... # Definir la tubería de modelación scaler = StandardScaler() modelo = LogisticRegression(solver=«Liberal»…) tubería = Oleoducto([[(‘s’,scaler),(‘m’,modelo)]) |
Enlazando todo esto, el ejemplo completo de la evaluación de un modelo de regresión logística sobre el conjunto de datos de la diabetes con todas las variables de entrada estandarizadas se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
# Evaluar un modelo de regresión logística en el conjunto de datos estandarizados de la diabetes de numpy importación significa de numpy importación std de pandas importación read_csv de sklearn.preprocesamiento importación LabelEncoder de sklearn.model_selection importación puntaje_valor_cruzado de sklearn.model_selection importación RepeatedStratifiedKFold de sklearn.tubería importación Oleoducto de sklearn.modelo_lineal importación LogisticRegression de sklearn.preprocesamiento importación StandardScaler # Cargar conjunto de datos url = ‘https://raw.githubusercontent.com/jbrownlee/Datasets/master/pima-indians-diabetes.csv’ dataframe = read_csv(url, encabezado=Ninguno) datos = dataframe.valores # Separados en elementos de entrada y salida X, y = datos[[:, :–1], datos[[:, –1] # Preparar mínimamente el conjunto de datos X = X.astype(«flotar) y = LabelEncoder().fit_transform(y.astype(«str)) # Definir la tubería de modelación scaler = StandardScaler() modelo = LogisticRegression(solver=«Liberal»…) tubería = Oleoducto([[(‘s’,scaler),(‘m’,modelo)]) # Definir el procedimiento de evaluación cv = RepeatedStratifiedKFold(n_splits=10, n_repeticiones=3, estado_aleatorio=1) # Evaluar el modelo m_scores = puntaje_valor_cruzado(tubería, X, y, puntuación=«exactitud, cv=cv, n_jobs=–1) # resumir el resultado imprimir(«Precisión: %.3f (%.3f) % (significa(m_scores), std(m_scores))) |
Al ejecutar el ejemplo se evalúa la tubería de modelación y se informa de la precisión de la media y la desviación estándar para ajustar un modelo de regresión logística en el conjunto de datos estandarizados.
Sus resultados específicos pueden diferir dada la naturaleza estocástica del algoritmo de aprendizaje, la naturaleza estocástica del procedimiento de evaluación y las diferencias de precisión entre las máquinas y las versiones de las bibliotecas. Intente ejecutar el ejemplo unas cuantas veces.
En este caso, podemos ver que la estandarización de todas las variables de entrada numéricas ha dado lugar a un aumento de la precisión de la clasificación media del 76,8 por ciento con un modelo evaluado en el conjunto de datos en bruto a alrededor del 77,2 por ciento para un modelo evaluado en el conjunto de datos con variables de entrada estandarizadas.
Hasta ahora, hemos aprendido que normalizar todas las variables no ayuda al rendimiento, pero normalizar todas las variables de entrada sí ayuda al rendimiento.
A continuación, exploremos si la aplicación selectiva de escalamiento a las variables de entrada puede ofrecer más mejoras.
Escalado selectivo de los insumos numéricos
Las transformaciones de datos pueden aplicarse selectivamente a las variables de entrada utilizando la clase de Transformador de Columna en scikit-learn.
Permite especificar la transformación (o tubería de transformaciones) a aplicar y los índices de las columnas a los que se aplican. Esto puede ser usado como parte de un modelo de tubería y evaluado usando validación cruzada.
Puedes aprender más sobre cómo usar el Transformador de Columna en el tutorial:
Podemos explorar el uso del Transformador de Columna para aplicar selectivamente la normalización y la estandarización a las variables de entrada numérica del conjunto de datos sobre la diabetes, a fin de ver si podemos lograr más mejoras en el rendimiento.
Normalizar sólo las variables de entrada no gausianas
En primer lugar, intentemos normalizar sólo las variables de entrada que no tienen una distribución de probabilidad de tipo gaussiano y dejemos el resto de las variables de entrada en estado bruto.
Podemos definir dos grupos de variables de entrada utilizando los índices de las columnas, uno para las variables con una distribución similar a la de Gauss y otro para las variables de entrada con una distribución similar a la exponencial.
|
... # Definir índices de columna para las variables con distribuciones «normales» y «exponenciales». norma_ix = [[1, 2, 5] exp_ix = [[0, 3, 4, 6, 7] |
Podemos entonces normalizar selectivamente el «exp_ix» y dejar que las otras variables de entrada pasen sin ninguna preparación de datos.
|
... # Definir las transformaciones selectivas t = [[(‘e’, MinMaxScaler(), exp_ix)] selectivo = Transformador de columna(transformadores=t, resto=«paso a través de) |
La transformación selectiva puede entonces ser usada como parte de nuestra tubería de modelación.
|
... # Definir la tubería de modelación modelo = LogisticRegression(solver=«Liberal»…) tubería = Oleoducto([[(‘s’,selectivo),(‘m’,modelo)]) |
Enlazando todo esto, a continuación se enumera el ejemplo completo de evaluación de un modelo de regresión logística de datos con normalización selectiva de algunas variables de entrada.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
# Evaluar un modelo de regresión logística en el conjunto de datos de la diabetes con normalización selectiva de numpy importación significa de numpy importación std de pandas importación read_csv de sklearn.preprocesamiento importación LabelEncoder de sklearn.model_selection importación puntaje_valor_cruzado de sklearn.model_selection importación RepeatedStratifiedKFold de sklearn.tubería importación Oleoducto de sklearn.modelo_lineal importación LogisticRegression de sklearn.preprocesamiento importación MinMaxScaler de sklearn.componer importación Transformador de columna # Cargar conjunto de datos url = ‘https://raw.githubusercontent.com/jbrownlee/Datasets/master/pima-indians-diabetes.csv’ dataframe = read_csv(url, encabezado=Ninguno) datos = dataframe.valores # Separados en elementos de entrada y salida X, y = datos[[:, :–1], datos[[:, –1] # Preparar mínimamente el conjunto de datos X = X.astype(«flotar) y = LabelEncoder().fit_transform(y.astype(«str)) # Definir índices de columna para las variables con distribuciones «normales» y «exponenciales». norma_ix = [[1, 2, 5] exp_ix = [[0, 3, 4, 6, 7] # Definir las transformaciones selectivas t = [[(‘e’, MinMaxScaler(), exp_ix)] selectivo = Transformador de columna(transformadores=t, resto=«paso a través de) # Definir la tubería de modelación modelo = LogisticRegression(solver=«Liberal»…) tubería = Oleoducto([[(‘s’,selectivo),(‘m’,modelo)]) # Definir el procedimiento de evaluación cv = RepeatedStratifiedKFold(n_splits=10, n_repeticiones=3, estado_aleatorio=1) # Evaluar el modelo m_scores = puntaje_valor_cruzado(tubería, X, y, puntuación=«exactitud, cv=cv, n_jobs=–1) # resumir el resultado imprimir(«Precisión: %.3f (%.3f) % (significa(m_scores), std(m_scores))) |
Al ejecutar el ejemplo se evalúa la tubería de modelación y se informa de la precisión de la media y la desviación estándar.
Sus resultados específicos pueden diferir dada la naturaleza estocástica del algoritmo de aprendizaje, la naturaleza estocástica del procedimiento de evaluación y las diferencias de precisión entre las máquinas y las versiones de las bibliotecas. Intente ejecutar el ejemplo unas cuantas veces.
En este caso, podemos ver un rendimiento ligeramente mejor, aumentando la precisión media con el ajuste del modelo base en el conjunto de datos en bruto con un 76,8 por ciento a cerca de 76,9 con la normalización selectiva de algunas variables de entrada.
Sin embargo, los resultados no son tan buenos como la estandarización de todas las variables de entrada.
Estandarizar sólo las variables de entrada de tipo gaussiano
Podemos repetir el experimento de la sección anterior, aunque en este caso, estandarizar selectivamente las variables de entrada que tienen una distribución similar a la de Gauss y dejar las restantes variables de entrada sin tocar.
|
... # Definir las transformaciones selectivas t = [[(‘n’, StandardScaler(), norma_ix)] selectivo = Transformador de columna(transformadores=t, resto=«paso a través de) |
Enlazando todo esto, a continuación se enumera el ejemplo completo de la evaluación de un modelo de regresión logística de datos con estandarización selectiva de algunas variables de entrada.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
# Evaluar un modelo de regresión logística en el conjunto de datos de la diabetes con estandarización selectiva de numpy importación significa de numpy importación std de pandas importación read_csv de sklearn.preprocesamiento importación LabelEncoder de sklearn.model_selection importación puntaje_valor_cruzado de sklearn.model_selection importación RepeatedStratifiedKFold de sklearn.tubería importación Oleoducto de sklearn.modelo_lineal importación LogisticRegression de sklearn.preprocesamiento importación StandardScaler de sklearn.componer importación Transformador de columna # Cargar conjunto de datos url = ‘https://raw.githubusercontent.com/jbrownlee/Datasets/master/pima-indians-diabetes.csv’ dataframe = read_csv(url, encabezado=Ninguno) datos = dataframe.valores # Separados en elementos de entrada y salida X, y = datos[[:, :–1], datos[[:, –1] # Preparar mínimamente el conjunto de datos X = X.astype(«flotar) y = LabelEncoder().fit_transform(y.astype(«str)) # Definir índices de columna para las variables con distribuciones «normales» y «exponenciales». norma_ix = [[1, 2, 5] exp_ix = [[0, 3, 4, 6, 7] # Definir las transformaciones selectivas t = [[(‘n’, StandardScaler(), norma_ix)] selectivo = Transformador de columna(transformadores=t, resto=«paso a través de) # Definir la tubería de modelación modelo = LogisticRegression(solver=«Liberal»…) tubería = Oleoducto([[(‘s’,selectivo),(‘m’,modelo)]) # Definir el procedimiento de evaluación cv = RepeatedStratifiedKFold(n_splits=10, n_repeticiones=3, estado_aleatorio=1) # Evaluar el modelo m_scores = puntaje_valor_cruzado(tubería, X, y, puntuación=«exactitud, cv=cv, n_jobs=–1) # resumir el resultado imprimir(«Precisión: %.3f (%.3f) % (significa(m_scores), std(m_scores))) |
Al ejecutar el ejemplo se evalúa la tubería de modelación y se informa de la precisión de la media y la desviación estándar.
Sus resultados específicos pueden diferir dada la naturaleza estocástica del algoritmo de aprendizaje, la naturaleza estocástica del procedimiento de evaluación y las diferencias de precisión entre las máquinas y las versiones de las bibliotecas. Intente ejecutar el ejemplo unas cuantas veces.
En este caso, podemos ver que logramos un aumento en el rendimiento tanto sobre el ajuste del modelo de base en el conjunto de datos en bruto con un 76,8% como sobre la estandarización de todas las variables de entrada que alcanzó un 77,2%. Con la estandarización selectiva, hemos logrado una precisión media de alrededor del 77,3 por ciento, un aumento modesto pero medible.
Normalizar y estandarizar selectivamente las variables de entrada
Los resultados obtenidos hasta ahora plantean la cuestión de si podemos conseguir un nuevo impulso combinando el uso de la normalización selectiva y la estandarización en el conjunto de datos al mismo tiempo.
Esto puede lograrse definiendo ambas transformaciones y sus respectivos índices de columna para la clase Transformador de Columna, sin que se pasen las variables restantes.
|
... # Definir las transformaciones selectivas t = [[(‘e’, MinMaxScaler(), exp_ix), (‘n’, StandardScaler(), norma_ix)] selectivo = Transformador de columna(transformadores=t) |
Enlazando todo esto, a continuación se enumera el ejemplo completo de evaluación de un modelo de regresión logística de datos con normalización selectiva y estandarización de las variables de entrada.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
# Evaluar un modelo de regresión logística en el conjunto de datos de la diabetes con escalamiento selectivo de numpy importación significa de numpy importación std de pandas importación read_csv de sklearn.preprocesamiento importación LabelEncoder de sklearn.model_selection importación puntaje_valor_cruzado de sklearn.model_selection importación RepeatedStratifiedKFold de sklearn.tubería importación Oleoducto de sklearn.modelo_lineal importación LogisticRegression de sklearn.preprocesamiento importación MinMaxScaler de sklearn.preprocesamiento importación StandardScaler de sklearn.componer importación Transformador de columna # Cargar conjunto de datos url = ‘https://raw.githubusercontent.com/jbrownlee/Datasets/master/pima-indians-diabetes.csv’ dataframe = read_csv(url, encabezado=Ninguno) datos = dataframe.valores # Separados en elementos de entrada y salida X, y = datos[[:, :–1], datos[[:, –1] # Preparar mínimamente el conjunto de datos X = X.astype(«flotar) y = LabelEncoder().fit_transform(y.astype(«str)) # Definir índices de columna para las variables con distribuciones «normales» y «exponenciales». norma_ix = [[1, 2, 5] exp_ix = [[0, 3, 4, 6, 7] # Definir las transformaciones selectivas t = [[(‘e’, MinMaxScaler(), exp_ix), (‘n’, StandardScaler(), norma_ix)] selectivo = Transformador de columna(transformadores=t) # Definir la tubería de modelación modelo = LogisticRegression(solver=«Liberal»…) tubería = Oleoducto([[(‘s’,selectivo),(‘m’,modelo)]) # Definir el procedimiento de evaluación cv = RepeatedStratifiedKFold(n_splits=10, n_repeticiones=3, estado_aleatorio=1) # Evaluar el modelo m_scores = puntaje_valor_cruzado(tubería, X, y, puntuación=«exactitud, cv=cv, n_jobs=–1) # resumir el resultado imprimir(«Precisión: %.3f (%.3f) % (significa(m_scores), std(m_scores))) |
Al ejecutar el ejemplo se evalúa la tubería de modelación y se informa de la precisión de la media y la desviación estándar.
Sus resultados específicos pueden diferir dada la naturaleza estocástica del algoritmo de aprendizaje, la naturaleza estocástica del procedimiento de evaluación y las diferencias de precisión entre las máquinas y las versiones de las bibliotecas. Intente ejecutar el ejemplo unas cuantas veces.
En este caso, curiosamente, podemos ver que hemos logrado el mismo rendimiento que al estandarizar todas las variables de entrada con un 77,2 por ciento.
Además, los resultados sugieren que el modelo elegido funciona mejor cuando las variables no similares a las de Gauss se dejan tal como están, que cuando se estandarizan o normalizan.
No habría adivinado este hallazgo, que pone de relieve la importancia de una cuidadosa experimentación.
¿Puedes hacerlo mejor?
Pruebe otras transformaciones o combinaciones de transformaciones y vea si puede lograr mejores resultados.
Comparta sus hallazgos en los comentarios siguientes.
Más lecturas
Esta sección proporciona más recursos sobre el tema si desea profundizar en él.
Tutoriales
APIs
Resumen
En este tutorial, descubriste cómo aplicar el escalado selectivo de las variables de entrada numérica.
Específicamente, aprendiste:
- Cómo cargar y calcular una línea base de rendimiento predictivo para el conjunto de datos de clasificación de la diabetes.
- Cómo evaluar la modelización de las tuberías con las transformaciones de datos aplicadas a ciegas a todas las variables de entrada numéricas.
- Cómo evaluar la modelización de tuberías con normalización y estandarización selectivas aplicadas a subconjuntos de variables de entrada.
