Cómo configurar la validación cruzada de k-Fold

El procedimiento de validación cruzada de pliegue k es un método estándar para estimar el rendimiento de un algoritmo de aprendizaje automático en un conjunto de datos.

Un valor común para k es 10, aunque ¿cómo sabemos que esta configuración es apropiada para nuestro conjunto de datos y nuestros algoritmos?

Un enfoque es explorar el efecto de diferentes k en la estimación del rendimiento del modelo y compararlo con una condición de prueba ideal. Esto puede ayudar a elegir un valor apropiado para k.

Una vez que un k-se elige el valor, puede utilizarse para evaluar un conjunto de diferentes algoritmos en el conjunto de datos y la distribución de los resultados puede compararse con una evaluación de los mismos algoritmos utilizando una condición de prueba ideal para ver si están altamente correlacionados o no. Si están correlacionados, confirma que la configuración elegida es una aproximación robusta para la condición de prueba ideal.

En este tutorial, descubrirá cómo configurar y evaluar configuraciones de validación cruzada de pliegue k.

Después de completar este tutorial, lo sabrás:

Cómo evaluar un algoritmo de aprendizaje de una máquina usando la validación cruzada de k-fold en un conjunto de datos.
Cómo realizar un análisis de sensibilidad de los valores k para la validación cruzada de k.
Cómo calcular la correlación entre un arnés de prueba de validación cruzada y una condición de prueba ideal.

Empecemos.

Cómo configurar la validación cruzada de k-Fold

Resumen del Tutorial

Este tutorial está dividido en tres partes; son:

Validación cruzada de k-Fold
Análisis de sensibilidad para k

Correlación del arnés de prueba con el objetivo

Validación cruzada de k-Fold

Es común evaluar los modelos de aprendizaje de las máquinas en un conjunto de datos utilizando la validación cruzada del pliegue k.

El procedimiento de validación cruzada de pliegues k divide un conjunto limitado de datos en pliegues k no superpuestos. Cada uno de los pliegues k tiene la oportunidad de ser utilizado como un conjunto de pruebas de retención, mientras que todos los demás pliegues colectivamente se utilizan como un conjunto de datos de entrenamiento. Un total de k modelos son ajustados y evaluados en los conjuntos de pruebas de retención k y se informa del rendimiento medio.

Para más información sobre el procedimiento de validación cruzada de k-fold, vea el tutorial:

El procedimiento de validación cruzada de k-fold puede ser implementado fácilmente usando la biblioteca de aprendizaje de la máquina scikit-learn.

Primero, definamos un conjunto de datos de clasificación sintética que podamos usar como base de este tutorial.

La función make_classification() puede utilizarse para crear un conjunto de datos de clasificación binaria sintética. La configuraremos para generar 100 muestras cada una con 20 características de entrada, 15 de las cuales contribuyen a la variable objetivo.

El ejemplo que figura a continuación crea y resume el conjunto de datos.

# Conjunto de datos de clasificación de pruebas de sklearn.datasets importar make_classification # Definir el conjunto de datos X, y = make_classification(n_samples=100, n_features=20, n_informative=15, n_redundant=5, random_state=1) # resumir el conjunto de datos impresión (forma X, forma Y)

# Conjunto de datos de clasificación de pruebas

de sklearn.conjuntos de datos importación hacer_clasificación

# Definir el conjunto de datos

X, y = make_classification(n_muestras=100, n_funciones=20, n_informativo=15, n_redundante=5, estado_aleatorio=1)

# resumir el conjunto de datos

imprimir(X.forma, y.forma)

Ejecutando el ejemplo se crea el conjunto de datos y se confirma que contiene 100 muestras y 10 variables de entrada.

La semilla fija para el generador de números pseudoaleatorios asegura que obtengamos las mismas muestras cada vez que se genera el conjunto de datos.

A continuación, podemos evaluar un modelo en este conjunto de datos utilizando la validación cruzada del pliegue k.

Evaluaremos un modelo de LogisticRegression y usaremos la clase KFold para realizar la validación cruzada, configurada para barajar el conjunto de datos y establecer k=10, un valor predeterminado popular.

La función cross_val_score() se utilizará para realizar la evaluación, tomando la configuración del conjunto de datos y la validación cruzada y devolviendo una lista de las puntuaciones calculadas para cada pliegue.

El ejemplo completo figura a continuación.

# Evaluar un modelo de regresión logística usando validación cruzada de pliegue k de la importación numérica significa de numpy import std de sklearn.datasets importar make_classification de sklearn.model_selection import KFold de sklearn.model_selection import cross_val_score de sklearn.linear_model import LogisticRegression # Crear un conjunto de datos X, y = make_classification(n_samples=100, n_features=20, n_informative=15, n_redundant=5, random_state=1) # Preparar el procedimiento de validación cruzada cv = KFold(n_splits=10, random_state=1, shuffle=True) # Crear un modelo modelo = LogisticRegression() # Evaluar el modelo puntuación = cross_val_score(modelo, X, y, puntuación=’precisión’, cv=cv, n_jobs=-1) # Informe de rendimiento print(‘Precisión: %.3f (%.3f)’ % (media(puntuaciones), std(puntuaciones))

# Evaluar un modelo de regresión logística usando validación cruzada de pliegue k

de numpy importación significa

de numpy importación std

de sklearn.conjuntos de datos importación make_classification

de sklearn.model_selection importación KFold

de sklearn.model_selection importación puntaje_valor_cruzado

de sklearn.modelo_lineal importación LogisticRegression

# Crear un conjunto de datos

X, y = make_classification(n_muestras=100, n_funciones=20, n_informativo=15, n_redundante=5, estado_aleatorio=1)

# Preparar el procedimiento de validación cruzada

cv = KFold(n_splits=10, estado_aleatorio=1, shuffle=Verdadero)

# Crear un modelo

modelo = LogisticRegression()

# Evaluar el modelo

resultados = puntaje_valor_cruzado(modelo, X, y, puntuación=«exactitud, cv=cv, n_jobs=–1)

# Informe de rendimiento

imprimir(«Precisión: %.3f (%.3f) % (significa(resultados), std(resultados)))

Ejecutando el ejemplo se crea el conjunto de datos, y luego se evalúa un modelo de regresión logística en él usando una validación cruzada de 10 veces. La precisión de la clasificación media en el conjunto de datos es entonces reportada.

Sus resultados específicos pueden variar dada la naturaleza estocástica del algoritmo de aprendizaje. Intente ejecutar el ejemplo unas cuantas veces.

En este caso, podemos ver que el modelo alcanzó una precisión de clasificación estimada de alrededor del 85,0 por ciento.

Ahora que estamos familiarizados con la validación cruzada del pliegue K, veamos cómo podríamos configurar el procedimiento.

Análisis de sensibilidad para k

El parámetro clave de configuración para la validación cruzada de pliegues k es k, que define el número de pliegues en el que se puede dividir un conjunto de datos determinado.

Los valores comunes son k=3, k=5 y k=10, y con mucho el valor más popular usado en el aprendizaje aplicado de la máquina para evaluar los modelos es k=10. La razón de esto es que se realizaron estudios y se encontró que k=10 proporciona un buen equilibrio entre el bajo costo computacional y el bajo sesgo en una estimación del rendimiento del modelo.

¿Cómo sabemos qué valor de k usar cuando evaluamos modelos en nuestro propio conjunto de datos?

Puedes elegir k=10, pero ¿cómo sabes que esto tiene sentido para tu conjunto de datos?

Una forma de responder a esta pregunta es realizar un análisis de sensibilidad para diferentes valores de k. Es decir, evaluar el rendimiento del mismo modelo en el mismo conjunto de datos con diferentes valores de k y ver cómo se comparan.

Se espera que los valores bajos de k den como resultado una estimación ruidosa del rendimiento del modelo y que los valores grandes de k den como resultado una estimación menos ruidosa del rendimiento del modelo.

¿Pero ruidoso comparado con qué?

No conocemos el verdadero rendimiento del modelo al hacer predicciones sobre datos nuevos/no vistos, ya que no tenemos acceso a los datos nuevos/no vistos. Si lo supiéramos, lo utilizaríamos en la evaluación del modelo.

Sin embargo, podemos elegir una condición de prueba que represente un «ideal«o como mejor podamos conseguir»ideal» estimación del rendimiento del modelo.

Un enfoque sería entrenar el modelo con todos los datos disponibles y estimar el rendimiento en un conjunto de datos separado, grande y representativo. El rendimiento en este conjunto de datos de reserva representaría el «modelo de la vida».verdadero«El rendimiento del modelo y cualquier rendimiento de validación cruzada en el conjunto de datos de entrenamiento representaría una estimación de este resultado.

Esto es raramente posible ya que a menudo no tenemos suficientes datos para retener algunos y utilizarlos como un conjunto de pruebas. Las competiciones de aprendizaje de máquinas de kaggle son una excepción a esto, donde tenemos un conjunto de pruebas de retención, una muestra de las cuales se evalúa a través de presentaciones.

En su lugar, podemos simular este caso usando la validación cruzada de no hacer nada (LOOCV), una versión computacionalmente costosa de la validación cruzada en la que k=N…y… N es el número total de ejemplos en el conjunto de datos de entrenamiento. Es decir, cada muestra del conjunto de capacitación recibe un ejemplo para ser utilizado solo como el conjunto de datos de evaluación de la prueba. Rara vez se utiliza para conjuntos de datos grandes, ya que es costoso desde el punto de vista computacional, aunque puede proporcionar una buena estimación del rendimiento del modelo, dados los datos disponibles.

Podemos entonces comparar la precisión de la clasificación media para diferentes valores k con la precisión de la clasificación media de LOOCV en el mismo conjunto de datos. La diferencia entre las puntuaciones proporciona una aproximación aproximada de lo bien que un valor k se aproxima a la condición ideal de la prueba de evaluación del modelo.

Exploremos cómo implementar un análisis de sensibilidad de validación cruzada de pliegue k.

Primero, definamos una función para crear el conjunto de datos. Esto te permite cambiar el conjunto de datos a tu propio conjunto si lo deseas.

# Crear el conjunto de datos def get_dataset(n_samples=100): X, y = make_classification(n_samples=n_samples, n_features=20, n_informative=15, n_redundant=5, random_state=1) devuelve X, y

# Crear el conjunto de datos

def get_dataset(n_muestras=100):

X, y = make_classification(n_muestras=n_muestras, n_funciones=20, n_informativo=15, n_redundante=5, estado_aleatorio=1)

volver X, y

A continuación, podemos definir un conjunto de datos para crear el modelo a evaluar.

Una vez más, esta separación le permite cambiar el modelo a su propio modelo si lo desea.

# Recuperar el modelo a evaluar def get_model(): model = LogisticRegression() modelo de retorno

# Recuperar el modelo a evaluar

def get_model():

modelo = LogisticRegression()

volver modelo

A continuación, puede definir una función para evaluar el modelo en el conjunto de datos dada una condición de prueba. La condición de prueba podría ser una instancia del KFold configurada con un valor k dado, o podría ser una instancia del LeaveOneOut que representa nuestra condición de prueba ideal.

La función devuelve la precisión de la clasificación media así como la precisión mínima y máxima de los pliegues. Podemos usar el mínimo y el máximo para resumir la distribución de las puntuaciones.

# Evaluar el modelo usando una condición de prueba dada def evaluate_model(cv): # Obtener el conjunto de datos X, y = get_dataset() # Consigue el modelo modelo = get_model() # Evaluar el modelo puntuación = cross_val_score(modelo, X, y, puntuación=’precisión’, cv=cv, n_jobs=-1) # devuelve las puntuaciones devuelve media(puntuaciones), puntuaciones.min(), puntuaciones.max()

# Evaluar el modelo usando una condición de prueba dada

def evaluate_model(cv):

# Obtener el conjunto de datos

X, y = get_dataset()

# Consigue el modelo

modelo = get_model()

# Evaluar el modelo

resultados = puntaje_valor_cruzado(modelo, X, y, puntuación=«exactitud, cv=cv, n_jobs=–1)

# devuelve las puntuaciones

volver significa(resultados), resultados.min(), resultados.max()

A continuación, podemos calcular el rendimiento del modelo usando el procedimiento LOOCV.

… # Calcular la condición ideal de la prueba ideal, _, _ = evaluar_modelo(LeaveOneOut()) print(‘Ideal: %.3f’ % ideal)

...

# Calcular la condición ideal de la prueba

ideal, _, _ = evaluate_model(LeaveOneOut())

imprimir(«Ideal: %.3f % ideal)

Podemos entonces definir los valores k a evaluar. En este caso, probaremos valores entre 2 y 30.

… # Definir los pliegues para probar pliegues = rango(2,31)

...

# Definir los pliegues para probar

pliegues = rango(2,31)

Podemos entonces evaluar cada valor a su vez y almacenar los resultados a medida que avanzamos.

… # Registrar la media y el min/max de cada conjunto de resultados significa, mins, maxs = list(),list(),list() # Evaluar cada valor de k por k en los pliegues: # definir la condición de prueba cv = KFold(n_splits=k, shuffle=True, random_state=1) # Evaluar el valor de k k_mean, k_min, k_max = evaluate_model(cv) # Informe de rendimiento print(‘> folds=%d, accuracy=%.3f (%.3f,%.3f)’ % (k, k_mean, k_min, k_max)) # Almacenar la precisión media means.append(k_mean) # Almacena los mínimos y máximos relativos a la media mins.append(k_mean – k_min) maxs.append(k_max – k_mean)

...

# Registrar la media y el min/max de cada conjunto de resultados

significa, mins, maxs = lista(),lista(),lista()

# Evaluar cada valor de k

para k en pliegues:

# Definir la condición de la prueba

cv = KFold(n_splits=k, shuffle=Verdadero, estado_aleatorio=1)

# Evaluar el valor de k

k_mean, k_min, k_max = evaluate_model(cv)

# Informe de rendimiento

imprimir(‘> pliegues=%d, precisión=%.3f (%.3f,%.3f)’ % (k, k_mean, k_min, k_max))

# Almacenar la precisión media

significa.anexar(k_mean)

# Almacena los mínimos y máximos relativos a la media

mins.anexar(k_mean – k_min)

maxs.anexar(k_max – k_mean)

Finalmente, podemos trazar los resultados para su interpretación.

… # Gráfica de línea de valores medios de k con barras de error mínimo/máximo pyplot.errorbar(folds, means, yerr=[mins, maxs], fmt=»o») # Trama el caso ideal en un color separado pyplot.plot(pliegues, [ideal for _ in range(len(folds))], color=»r») # mostrar la trama pyplot.show()

...

# Gráfica de línea de valores medios de k con barras de error min/max

pyplot.barra de error(pliegues, significa, yerr=[[mins, maxs], fmt=‘o’)

# Trama el caso ideal en un color separado

pyplot.parcela(pliegues, [[ideal para _ en rango(len(pliegues))], color=‘r’)

# mostrar la trama

pyplot.mostrar()

A continuación se muestra el ejemplo completo.

# Análisis de sensibilidad de k en validación cruzada de k de la importación numérica significa de sklearn.datasets importar make_classification de sklearn.model_selection import LeaveOneOut de sklearn.model_selection import KFold de sklearn.model_selection import cross_val_score de sklearn.linear_model import LogisticRegression de matplotlib import pyplot # Crear el conjunto de datos def get_dataset(n_samples=100): X, y = make_classification(n_samples=n_samples, n_features=20, n_informative=15, n_redundant=5, random_state=1) devuelve X, y # Recuperar el modelo a evaluar def get_model(): model = LogisticRegression() modelo de retorno # Evaluar el modelo usando una condición de prueba dada def evaluate_model(cv): # Obtener el conjunto de datos X, y = get_dataset() # Consigue el modelo modelo = get_model() # Evaluar el modelo puntuación = cross_val_score(modelo, X, y, puntuación=’precisión’, cv=cv, n_jobs=-1) # devuelve las puntuaciones devuelve media(puntuaciones), puntuaciones.min(), puntuaciones.max() # Calcular la condición ideal de la prueba ideal, _, _ = evaluar_modelo(LeaveOneOut()) print(‘Ideal: %.3f’ % ideal) # Definir los pliegues para probar pliegues = rango(2,31) # Registra la media y el min/max de cada conjunto de resultados significa, mins, maxs = list(),list(),list() # Evaluar cada valor de k por k en los pliegues: # definir la condición de prueba cv = KFold(n_splits=k, shuffle=True, random_state=1) # Evaluar el valor de k k_mean, k_min, k_max = evaluate_model(cv) # Informe de rendimiento print(‘> folds=%d, accuracy=%.3f (%.3f,%.3f)’ % (k, k_mean, k_min, k_max)) # Almacenar la precisión media means.append(k_mean) # Almacena los mínimos y máximos relativos a la media mins.append(k_mean – k_min) maxs.append(k_max – k_mean) # Gráfica de línea de valores medios de k con barras de error min/max pyplot.errorbar(folds, means, yerr=[mins, maxs], fmt=»o») # Trama el caso ideal en un color separado pyplot.plot(pliegues, [ideal for _ in range(len(folds))], color=»r») # mostrar la trama pyplot.show()

# Análisis de sensibilidad de k en validación cruzada de k

de numpy importación significa

de sklearn.conjuntos de datos importación make_classification

de sklearn.model_selection importación LeaveOneOut

de sklearn.model_selection importación KFold

de sklearn.model_selection importación puntaje_valor_cruzado

de sklearn.modelo_lineal importación LogisticRegression

de matplotlib importación pyplot

# Crear el conjunto de datos

def get_dataset(n_muestras=100):

X, y = make_classification(n_muestras=n_muestras, n_funciones=20, n_informativo=15, n_redundante=5, estado_aleatorio=1)

volver X, y

# Recuperar el modelo a evaluar

def get_model():

modelo = LogisticRegression()

volver modelo

# Evaluar el modelo usando una condición de prueba dada

def evaluate_model(cv):

# Obtener el conjunto de datos

X, y = get_dataset()

# Consigue el modelo

modelo = get_model()

# Evaluar el modelo

resultados = puntaje_valor_cruzado(modelo, X, y, puntuación=«exactitud, cv=cv, n_jobs=–1)

# devuelve las puntuaciones

volver significa(resultados), resultados.min(), resultados.max()

# Calcular la condición ideal de la prueba

ideal, _, _ = evaluate_model(LeaveOneOut())

imprimir(«Ideal: %.3f % ideal)

# Definir los pliegues para probar

pliegues = rango(2,31)

# Registrar la media y el min/max de cada conjunto de resultados

significa, mins, maxs = lista(),lista(),lista()

# Evaluar cada valor de k

para k en pliegues:

# Definir la condición de la prueba

cv = KFold(n_splits=k, shuffle=Verdadero, estado_aleatorio=1)

# Evaluar el valor de k

k_mean, k_min, k_max = evaluate_model(cv)

# Informe de rendimiento

imprimir(‘> pliegues=%d, precisión=%.3f (%.3f,%.3f)’ % (k, k_mean, k_min, k_max))

# Almacenar la precisión media

significa.anexar(k_mean)

# Almacena los mínimos y máximos relativos a la media

mins.anexar(k_mean – k_min)

maxs.anexar(k_max – k_mean)

# Gráfica de línea de valores medios de k con barras de error min/max

pyplot.barra de error(pliegues, significa, yerr=[[mins, maxs], fmt=‘o’)

# Trama el caso ideal en un color separado

pyplot.parcela(pliegues, [[ideal para _ en rango(len(pliegues))], color=‘r’)

# mostrar la trama

pyplot.mostrar()

Ejecutando el ejemplo primero se reporta el LOOCV, luego la media, min, y máxima precisión para cada valor k que fue evaluado.

Sus resultados específicos pueden variar dada la naturaleza estocástica del algoritmo de aprendizaje. Intente ejecutar el ejemplo unas cuantas veces.

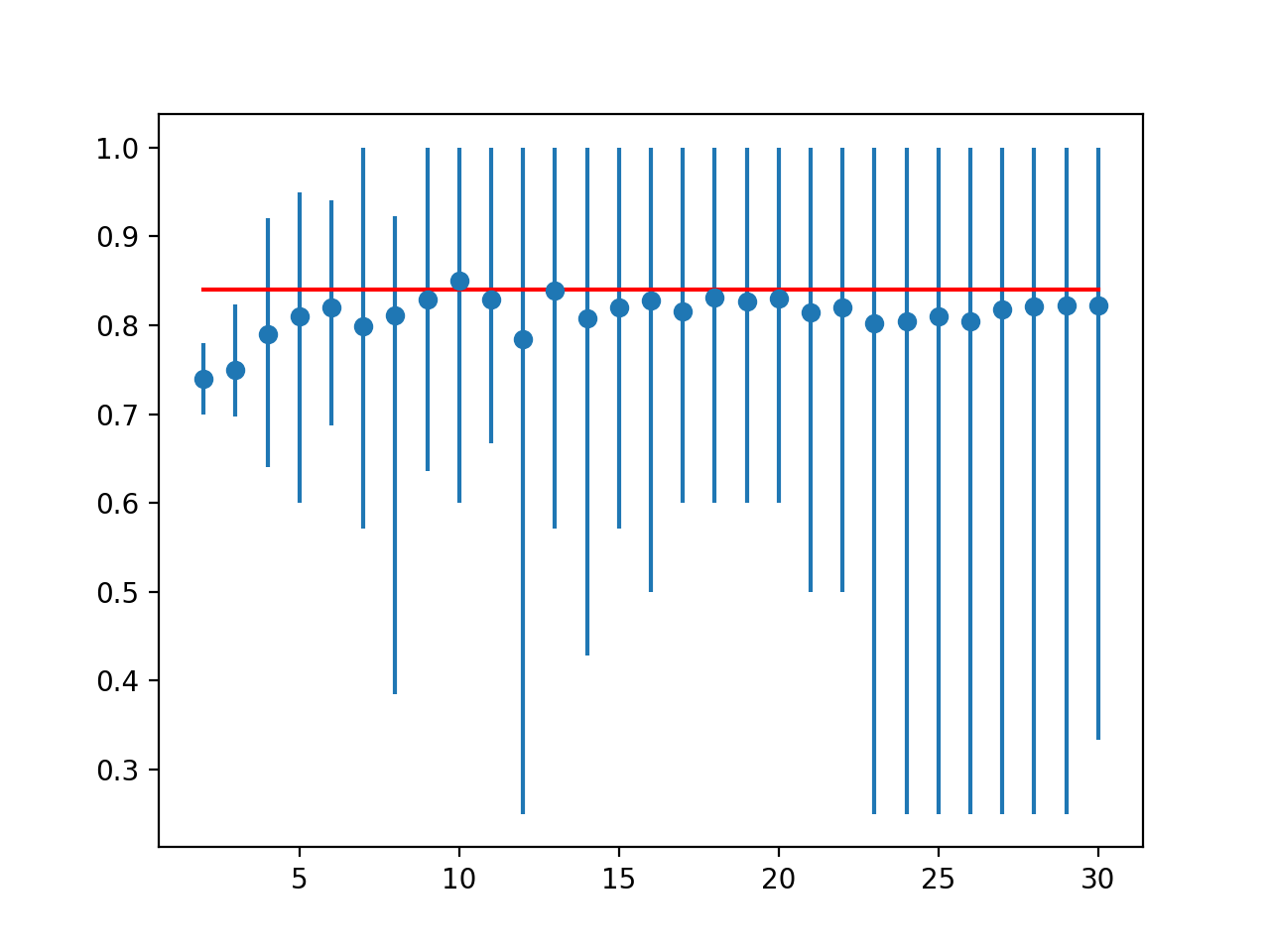
En este caso, podemos ver que el resultado del LOOCV fue de alrededor del 84 por ciento, ligeramente inferior al resultado k=10 del 85 por ciento.

Ideal: 0.840 > pliegues=2, precisión=0,740 (0,700,0,780) > pliegues=3, precisión=0,749 (0,697,0,824) > pliegues=4, precisión=0,790 (0,640,0,920) > pliegues=5, precisión=0,810 (0,600,0,950) > pliegues=6, precisión=0,820 (0,688,0,941) > pliegues=7, precisión=0.799 (0.571,1.000) > pliegues=8, precisión=0,811 (0,385,0,923) > pliegues=9, precisión=0.829 (0.636,1.000) > pliegues=10, precisión=0.850 (0.600,1.000) > pliegues=11, precisión=0.829 (0.667,1.000) > pliegues=12, precisión=0.785 (0.250,1.000) > pliegues=13, precisión=0.839 (0.571,1.000) > pliegues=14, precisión=0.807 (0.429,1.000) > pliegues=15, precisión=0.821 (0.571,1.000) > pliegues=16, precisión=0.827 (0.500,1.000) > pliegues=17, precisión=0.816 (0.600,1.000) > pliegues=18, precisión=0.831 (0.600,1.000) > pliegues=19, precisión=0.826 (0.600,1.000) > pliegues=20, precisión=0.830 (0.600,1.000) > pliegues=21, precisión=0.814 (0.500,1.000) > pliegues=22, precisión=0.820 (0.500,1.000) > pliegues=23, precisión=0.802 (0.250,1.000) > pliegues=24, precisión=0.804 (0.250,1.000) > pliegues=25, precisión=0.810 (0.250,1.000) > pliegues=26, precisión=0.804 (0.250,1.000) > pliegues=27, precisión=0.818 (0.250,1.000) > pliegues=28, precisión=0.821 (0.250,1.000) > pliegues=29, precisión=0.822 (0.250,1.000) > pliegues=30, precisión=0.822 (0.333,1.000)

Ideal: 0.840

> pliegues=2, precisión=0,740 (0,700,0,780)

> pliegues=3, precisión=0,749 (0,697,0,824)

> pliegues=4, precisión=0,790 (0,640,0,920)

> pliegues=5, precisión=0,810 (0,600,0,950)

> pliegues=6, precisión=0,820 (0,688,0,941)

> pliegues=7, precisión=0.799 (0.571,1.000)

> pliegues=8, precisión=0,811 (0,385,0,923)

> pliegues=9, precisión=0.829 (0.636,1.000)

> pliegues=10, precisión=0.850 (0.600,1.000)

> pliegues=11, precisión=0.829 (0.667,1.000)

> pliegues=12, precisión=0.785 (0.250,1.000)

> pliegues=13, precisión=0.839 (0.571,1.000)

> pliegues=14, precisión=0.807 (0.429,1.000)

> pliegues=15, precisión=0.821 (0.571,1.000)

> pliegues=16, precisión=0.827 (0.500,1.000)

> pliegues=17, precisión=0.816 (0.600,1.000)

> pliegues=18, precisión=0.831 (0.600,1.000)

> pliegues=19, precisión=0.826 (0.600,1.000)

> pliegues=20, precisión=0.830 (0.600,1.000)

> pliegues=21, precisión=0.814 (0.500,1.000)

> pliegues=22, precisión=0.820 (0.500,1.000)

> pliegues=23, precisión=0.802 (0.250,1.000)

> pliegues=24, precisión=0.804 (0.250,1.000)

> pliegues=25, precisión=0.810 (0.250,1.000)

> pliegues=26, precisión=0.804 (0.250,1.000)

> pliegues=27, precisión=0.818 (0.250,1.000)

> pliegues=28, precisión=0.821 (0.250,1.000)

> pliegues=29, precisión=0.822 (0.250,1.000)

> pliegues=30, precisión=0.822 (0.333,1.000)

Se crea un gráfico de líneas que compara las puntuaciones medias de precisión con el resultado de la LOOCV con el mínimo y el máximo de cada distribución de resultados indicada mediante barras de error.

Los resultados sugieren que para este modelo en este conjunto de datos, la mayoría de los valores k subestiman el rendimiento del modelo en comparación con el caso ideal. Los resultados sugieren que quizás k=10 por sí solo es ligeramente optimista y quizás k=13 podría ser una estimación más precisa.

Trazado de líneas de precisión media para la validación cruzada de los valores k con barras de error (azul) contra el caso ideal (rojo)

Esto proporciona una plantilla que puede utilizarse para realizar un análisis de sensibilidad de los valores k de su modelo elegido en su conjunto de datos contra una condición de prueba ideal dada.

Correlación del arnés de prueba con el objetivo

Una vez que se elige un arnés de prueba, otra consideración es cuán bien se ajusta a la condición de prueba ideal a través de los diferentes algoritmos.

Es posible que para algunos algoritmos y algunas configuraciones, la validación cruzada del pliegue k sea una mejor aproximación de la condición de prueba ideal en comparación con otros algoritmos y configuraciones de algoritmos.

Podemos evaluar e informar sobre esta relación explícitamente. Esto puede lograrse calculando cuán bien los resultados de la validación cruzada de k en un rango de algoritmos coinciden con la evaluación de los mismos algoritmos en la condición de prueba ideal.

El coeficiente de correlación de Pearson puede calcularse entre los dos grupos de puntuaciones para medir cuán cerca están. Es decir, ¿cambian juntos de la misma manera: cuando un algoritmo se ve mejor que otro a través de la validación cruzada de pliegues k, ¿se mantiene la condición ideal de la prueba?

Esperamos ver una fuerte correlación positiva entre las puntuaciones, como 0,5 o más. Una baja correlación sugiere la necesidad de cambiar el arnés de pruebas de validación cruzada de k para que se ajuste mejor a la condición de prueba ideal.

Primero, podemos definir una función que creará una lista de modelos estándar de aprendizaje de máquinas para evaluar a través de cada arnés de prueba.

# Obtener una lista de modelos para evaluar def get_models(): models = list() models.append(LogisticRegression()) models.append(RidgeClassifier()) models.append(SGDClassifier()) models.append(PassiveAggressiveClassifier()) models.append(KNeighborsClassifier()) models.append(DecisionTreeClassifier()) models.append(ExtraTreeClassifier()) models.append(LinearSVC()) models.append(SVC()) models.append(GaussianNB()) models.append(AdaBoostClassifier()) models.append(BaggingClassifier()) models.append(RandomForestClassifier()) models.append(ExtraTreesClassifier()) models.append(GaussianProcessClassifier()) models.append(GradientBoostingClassifier()) models.append(LinearDiscriminantAnalysis()) models.append(QuadraticDiscriminantAnalysis()) modelos de retorno

# Obtener una lista de modelos para evaluar

def get_models():

modelos = lista()

modelos.anexar(LogisticRegression())

modelos.anexar(RidgeClassifier())

modelos.anexar(Clasificador SGDC())

modelos.anexar(Clasificador Pasivo-Agresivo())

modelos.anexar(KNeighborsClassifier())

modelos.anexar(DecisionTreeClassifier())

modelos.anexar(ExtraTreeClassifier())

modelos.anexar(LinearSVC())

modelos.anexar(SVC())

modelos.anexar(GaussianNB())

modelos.anexar(AdaBoostClassifier())

modelos.anexar(BaggingClassifier())

modelos.anexar(RandomForestClassifier())

modelos.anexar(ExtraTreesClassifier())

modelos.anexar(GaussianProcessClassifier())

modelos.anexar(GradientBoostingClassifier())

modelos.anexar(LinearDiscriminantAnalysis())

modelos.anexar(QuadraticDiscriminantAnalysis())

volver modelos

Usaremos k=10 para el arnés de prueba elegido.

Podemos enumerar cada modelo y evaluarlo usando una validación cruzada de 10 veces y nuestra condición de prueba ideal, en este caso, LOOCV.

… # Definir las condiciones de la prueba ideal_cv = LeaveOneOut() cv = KFold(n_splits=10, shuffle=True, random_state=1) # Obtener la lista de modelos a considerar modelos = get_models() # recoger los resultados ideal_results, cv_results = list(), list() # Evaluar cada modelo para modelo en modelos: # Evaluar el modelo usando cada condición de prueba cv_mean = evaluate_model(cv, model) medio_ideal = evaluate_model(ideal_cv, model) # Revisar si hay resultados inválidos si es isan(cv_significado) o isan(ideal_significado): Continuar # Almacenar los resultados cv_results.append(cv_mean) ideal_results.append(ideal_significado) # Resumir el progreso… print(‘>%s: ideal=%.3f, cv=%.3f’ % (type(model).__name__, ideal_mean, cv_mean))

...

# Definir las condiciones de la prueba

ideal_cv = LeaveOneOut()

cv = KFold(n_splits=10, shuffle=Verdadero, estado_aleatorio=1)

# Obtener la lista de modelos a considerar

modelos = get_models()

# recoger los resultados

resultados_ideales, cv_resultados = lista(), lista()

# Evaluar cada modelo

para modelo en modelos:

# Evaluar el modelo usando cada condición de prueba

cv_mean = evaluate_model(cv, modelo)

medio_ideal = evaluate_model(ideal_cv, modelo)

# Revisar si hay resultados inválidos

si isan(cv_mean) o isan(medio_ideal):

Continúa

# Almacenar los resultados

cv_resultados.anexar(cv_mean)

resultados_ideales.anexar(medio_ideal)

# Resumir el progreso…

imprimir(‘>%s: ideal=%.3f, cv=%.3f’ % (escriba(modelo).__nombre__, medio_ideal, cv_mean))

Podemos entonces calcular la correlación entre la precisión de la clasificación media del arnés de prueba de validación cruzada de 10 veces y el arnés de prueba de LOOCV.

… # Calcular la correlación entre cada condición de prueba corr, _ = pearsonr(cv_results, ideal_results) print(‘Correlación: %.3f’ % corr)

...

# Calcular la correlación entre cada condición de prueba

corr, _ = pearsonr(cv_resultados, resultados_ideales)

imprimir(Correlación: %.3f’. % corr)

Finalmente, podemos crear un gráfico de dispersión de los dos conjuntos de resultados y dibujar una línea de mejor ajuste para ver visualmente lo bien que cambian juntos.

… # Gráfica de dispersión de resultados pyplot.scatter(cv_results, ideal_results) # trazar la línea de mejor ajuste coeficiente, sesgo = polyfit(cv_resultados, resultados_ideales, 1) line = coeff * asarray(cv_results) + bias pyplot.plot(cv_results, line, color=»r») # mostrar la trama pyplot.show()

...

# Gráfica de dispersión de resultados

pyplot.Dispersión(cv_resultados, resultados_ideales)

# trazar la línea de mejor ajuste

coeff, sesgo = polyfit(cv_resultados, resultados_ideales, 1)

línea = coeff * asarray(cv_resultados) + sesgo

pyplot.parcela(cv_resultados, línea, color=‘r’)

# mostrar la trama

pyplot.mostrar()

A continuación se muestra el ejemplo completo de todo esto.

# Correlación entre el arnés de prueba y la condición de prueba ideal de la importación numérica significa de numpy importan isan de la numpy importación asarray de la importación numpy polyfit de scipy.stats import pearsonr de matplotlib import pyplot de sklearn.datasets importar make_classification de sklearn.model_selection import KFold de sklearn.model_selection import LeaveOneOut de sklearn.model_selection import cross_val_score de sklearn.linear_model import LogisticRegression de sklearn.linear_model import RidgeClassifier de sklearn.linear_model importado SGDClassifier de sklearn.linear_model importado PassiveAggressiveClassifier de sklearn.neighbors importar KNeighborsClassifier de sklearn.tree import DecisionTreeClassifier de sklearn.tree import ExtraTreeClassifier de sklearn.svm import LinearSVC de sklearn.svm import SVC de sklearn.naive_bayes import GaussianNB de sklearn.ensemble importado AdaBoostClassifier de sklearn.ensemble importado BaggingClassifier de sklearn.ensemble import RandomForestClassifier de sklearn.ensemble import ExtraTreesClassifier de sklearn.gaussian_process import GaussianProcessClassifier de la importación de sklearn.ensemble GradientBoostingClassifier de sklearn.discriminant_analysis import LinearDiscriminantAnalysis de sklearn.discriminant_analysis import QuadraticDiscriminantAnalysis # Crear el conjunto de datos def get_dataset(n_samples=100): X, y = make_classification(n_samples=n_samples, n_features=20, n_informative=15, n_redundant=5, random_state=1) devuelve X, y # Obtener una lista de modelos para evaluar def get_models(): models = list() models.append(LogisticRegression()) models.append(RidgeClassifier()) models.append(SGDClassifier()) models.append(PassiveAggressiveClassifier()) models.append(KNeighborsClassifier()) models.append(DecisionTreeClassifier()) models.append(ExtraTreeClassifier()) models.append(LinearSVC()) models.append(SVC()) models.append(GaussianNB()) models.append(AdaBoostClassifier()) models.append(BaggingClassifier()) models.append(RandomForestClassifier()) models.append(ExtraTreesClassifier()) models.append(GaussianProcessClassifier()) models.append(GradientBoostingClassifier()) models.append(LinearDiscriminantAnalysis()) models.append(QuadraticDiscriminantAnalysis()) modelos de retorno # Evaluar el modelo usando una condición de prueba dada def evaluate_model(cv, model): # Obtener el conjunto de datos X, y = get_dataset() # Evaluar el modelo puntuación = cross_val_score(modelo, X, y, puntuación=’precisión’, cv=cv, n_jobs=-1) # devuelve las puntuaciones media de retorno (puntuaciones) # Definir las condiciones de la prueba ideal_cv = LeaveOneOut() cv = KFold(n_splits=10, shuffle=True, random_state=1) # Obtener la lista de modelos a considerar modelos = get_models() # recoger los resultados ideal_results, cv_results = list(), list() # Evaluar cada modelo para modelo en modelos: # Evaluar el modelo usando cada condición de prueba cv_mean = evaluate_model(cv, model) medio_ideal = evaluate_model(ideal_cv, model) # Revisar si hay resultados inválidos si es isan(cv_significado) o isan(ideal_significado): Continuar # Almacenar los resultados cv_results.append(cv_mean) ideal_results.append(ideal_significado) # Resumir el progreso… print(‘>%s: ideal=%.3f, cv=%.3f’ % (type(model).__name__, ideal_mean, cv_mean)) # Calcular la correlación entre cada condición de prueba corr, _ = pearsonr(cv_results, ideal_results) print(‘Correlación: %.3f’ % corr) # Gráfica de dispersión de resultados pyplot.scatter(cv_results, ideal_results) # trazar la línea de mejor ajuste coeficiente, sesgo = polyfit(cv_resultados, resultados_ideales, 1) line = coeff * asarray(cv_results) + bias pyplot.plot(cv_results, line, color=»r») # Etiquetar la trama pyplot.title(’10 veces CV vs LOOCV Precisión media’) pyplot.xlabel(‘Precisión media (CV 10 veces mayor)’) pyplot.ylabel(‘Precisión media (LOOCV)’) # mostrar la trama pyplot.show()

100

101

102

# Correlación entre el arnés de prueba y la condición de prueba ideal

de numpy importación significa

de numpy importación isan

de numpy importación asarray

de numpy importación polyfit

de scipy.estadísticas importación pearsonr

de matplotlib importación pyplot

de sklearn.conjuntos de datos importación make_classification

de sklearn.model_selection importación KFold

de sklearn.model_selection importación LeaveOneOut

de sklearn.model_selection importación puntaje_valor_cruzado

de sklearn.modelo_lineal importación LogisticRegression

de sklearn.modelo_lineal importación RidgeClassifier

de sklearn.modelo_lineal importación Clasificador SGDC

de sklearn.modelo_lineal importación Clasificador Pasivo-Agresivo

de sklearn.vecinos importación KNeighborsClassifier

de sklearn.árbol importación DecisionTreeClassifier

de sklearn.árbol importación ExtraTreeClassifier

de sklearn.svm importación LinearSVC

de sklearn.svm importación SVC

de sklearn.naive_bayes importación GaussianNB

de sklearn.conjunto importación AdaBoostClassifier

de sklearn.conjunto importación BaggingClassifier

de sklearn.conjunto importación RandomForestClassifier

de sklearn.conjunto importación ExtraTreesClassifier

de sklearn.PROCESO_GAUSIANO importación GaussianProcessClassifier

de sklearn.conjunto importación GradientBoostingClassifier

de sklearn.análisis_discriminatorio importación LinearDiscriminantAnalysis

de sklearn.análisis_discriminatorio importación QuadraticDiscriminantAnalysis

# Crear el conjunto de datos

def get_dataset(n_muestras=100):

X, y = make_classification(n_muestras=n_muestras, n_funciones=20, n_informativo=15, n_redundante=5, estado_aleatorio=1)

volver X, y

# Obtener una lista de modelos para evaluar

def get_models():

modelos = lista()

modelos.anexar(LogisticRegression())

modelos.anexar(RidgeClassifier())

modelos.anexar(Clasificador SGDC())

modelos.anexar(Clasificador Pasivo-Agresivo())

modelos.anexar(KNeighborsClassifier())

modelos.anexar(DecisionTreeClassifier())

modelos.anexar(ExtraTreeClassifier())

modelos.anexar(LinearSVC())

modelos.anexar(SVC())

modelos.anexar(GaussianNB())

modelos.anexar(AdaBoostClassifier())

modelos.anexar(BaggingClassifier())

modelos.anexar(RandomForestClassifier())

modelos.anexar(ExtraTreesClassifier())

modelos.anexar(GaussianProcessClassifier())

modelos.anexar(GradientBoostingClassifier())

modelos.anexar(LinearDiscriminantAnalysis())

modelos.anexar(QuadraticDiscriminantAnalysis())

volver modelos

# Evaluar el modelo usando una condición de prueba dada

def evaluate_model(cv, modelo):

# Obtener el conjunto de datos

X, y = get_dataset()

# Evaluar el modelo

resultados = puntaje_valor_cruzado(modelo, X, y, puntuación=«exactitud, cv=cv, n_jobs=–1)

# devuelve las puntuaciones

volver significa(resultados)

# Definir las condiciones de la prueba

ideal_cv = LeaveOneOut()

cv = KFold(n_splits=10, shuffle=Verdadero, estado_aleatorio=1)

# Obtener la lista de modelos a considerar

modelos = get_models()

# recoger los resultados

resultados_ideales, cv_resultados = lista(), lista()

# Evaluar cada modelo

para modelo en modelos:

# Evaluar el modelo usando cada condición de prueba

cv_mean = evaluate_model(cv, modelo)

medio_ideal = evaluate_model(ideal_cv, modelo)

# Revisar si hay resultados inválidos

si isan(cv_mean) o isan(medio_ideal):

Continúa

# Almacenar los resultados

cv_resultados.anexar(cv_mean)

resultados_ideales.anexar(medio_ideal)

# Resumir el progreso…

imprimir(‘>%s: ideal=%.3f, cv=%.3f’ % (escriba(modelo).__nombre__, medio_ideal, cv_mean))

# Calcular la correlación entre cada condición de prueba

corr, _ = pearsonr(cv_resultados, resultados_ideales)

imprimir(Correlación: %.3f’. % corr)

# Gráfica de dispersión de resultados

pyplot.Dispersión(cv_resultados, resultados_ideales)

# trazar la línea de mejor ajuste

coeff, sesgo = polyfit(cv_resultados, resultados_ideales, 1)

línea = coeff * asarray(cv_resultados) + sesgo

pyplot.parcela(cv_resultados, línea, color=‘r’)

# Etiquetar la trama

pyplot.título(«CV 10 veces más exacto que LOOCV)

pyplot.xlabel(Precisión media (CV 10 veces mayor)’.)

pyplot.ylabel(«Exactitud media (LOOCV))

# mostrar la trama

pyplot.mostrar()

La ejecución del ejemplo informa de la precisión de la clasificación media de cada algoritmo calculado mediante cada arnés de prueba.

Sus resultados específicos pueden variar dada la naturaleza estocástica del algoritmo de aprendizaje. Intente ejecutar el ejemplo unas cuantas veces.

Puede que vea algunas advertencias que puede ignorar con seguridad, como:

Podemos ver que para algunos algoritmos, el arnés de prueba sobreestima la precisión en comparación con el LOOCV, y en otros casos, subestima la precisión. Esto es de esperar.

Al final del recorrido, podemos ver que se informa de la correlación entre los dos conjuntos de resultados. En este caso, podemos ver que se informa de una correlación de 0,746, que es una buena correlación positiva fuerte. Los resultados sugieren que la validación cruzada de 10 veces proporciona una buena aproximación para el arnés de pruebas de LOOCV en este conjunto de datos, calculado con 18 algoritmos populares de aprendizaje de máquinas.

>Regresión logística: ideal=0.840, cv=0.850 >Clasificador de cumbres: ideal=0,830, cv=0,830 >SGDClassifier: ideal=0.730, cv=0.790 >Clasificador Pasivo-Agresivo: ideal=0.780, cv=0.760 >KNeighborsClassifier: ideal=0.760, cv=0.770 >Clasificador de Árbol de Decisión: ideal=0.690, cv=0.630 >ExtraTreeClassifier: ideal=0.710, cv=0.620 >SVC lineal: ideal=0.850, cv=0.830 >SVC: ideal=0.900, cv=0.880 >GaussianNB: ideal=0.730, cv=0.720 >AdaBoostClassifier: ideal=0.740, cv=0.740 >BaggingClassifier: ideal=0.770, cv=0.740 >Clasificador Forestal Aleatorio: ideal=0.810, cv=0.790 >ExtraTreesClassifier: ideal=0.820, cv=0.820 >Clasificador de Procesos Gaussiano: ideal=0.790, cv=0.760 >Clasificador de potenciación de gradiente: ideal=0.820, cv=0.820 >Análisis Discriminatorio Lineal: ideal=0.830, cv=0.830 >Análisis Cuadrático-Discriminatorio: ideal=0.610, cv=0.760 Correlación: 0.746

>Regresión logística: ideal=0.840, cv=0.850

>Clasificador de cumbres: ideal=0,830, cv=0,830

>SGDClassifier: ideal=0.730, cv=0.790

>Clasificador Pasivo-Agresivo: ideal=0.780, cv=0.760

>KNeighborsClassifier: ideal=0.760, cv=0.770

>Clasificador de Árbol de Decisión: ideal=0.690, cv=0.630

>ExtraTreeClassifier: ideal=0.710, cv=0.620

>SVC lineal: ideal=0.850, cv=0.830

>SVC: ideal=0.900, cv=0.880

>GaussianNB: ideal=0.730, cv=0.720

>AdaBoostClassifier: ideal=0.740, cv=0.740

>BaggingClassifier: ideal=0.770, cv=0.740

>Clasificador Forestal Aleatorio: ideal=0.810, cv=0.790

>ExtraTreesClassifier: ideal=0.820, cv=0.820

>Clasificador de Procesos Gaussiano: ideal=0.790, cv=0.760

>Clasificador de potenciación de gradiente: ideal=0.820, cv=0.820

>Análisis Discriminatorio Lineal: ideal=0.830, cv=0.830

>Análisis Cuadrático-Discriminatorio: ideal=0.610, cv=0.760

Correlación: 0.746

Finalmente, se crea un gráfico de dispersión que compara la distribución de las puntuaciones medias de precisión para el arnés de pruebas (eje x) con las puntuaciones de precisión a través de LOOCV (eje y).

Se dibuja una línea roja de mejor ajuste a través de los resultados que muestra la fuerte correlación lineal.

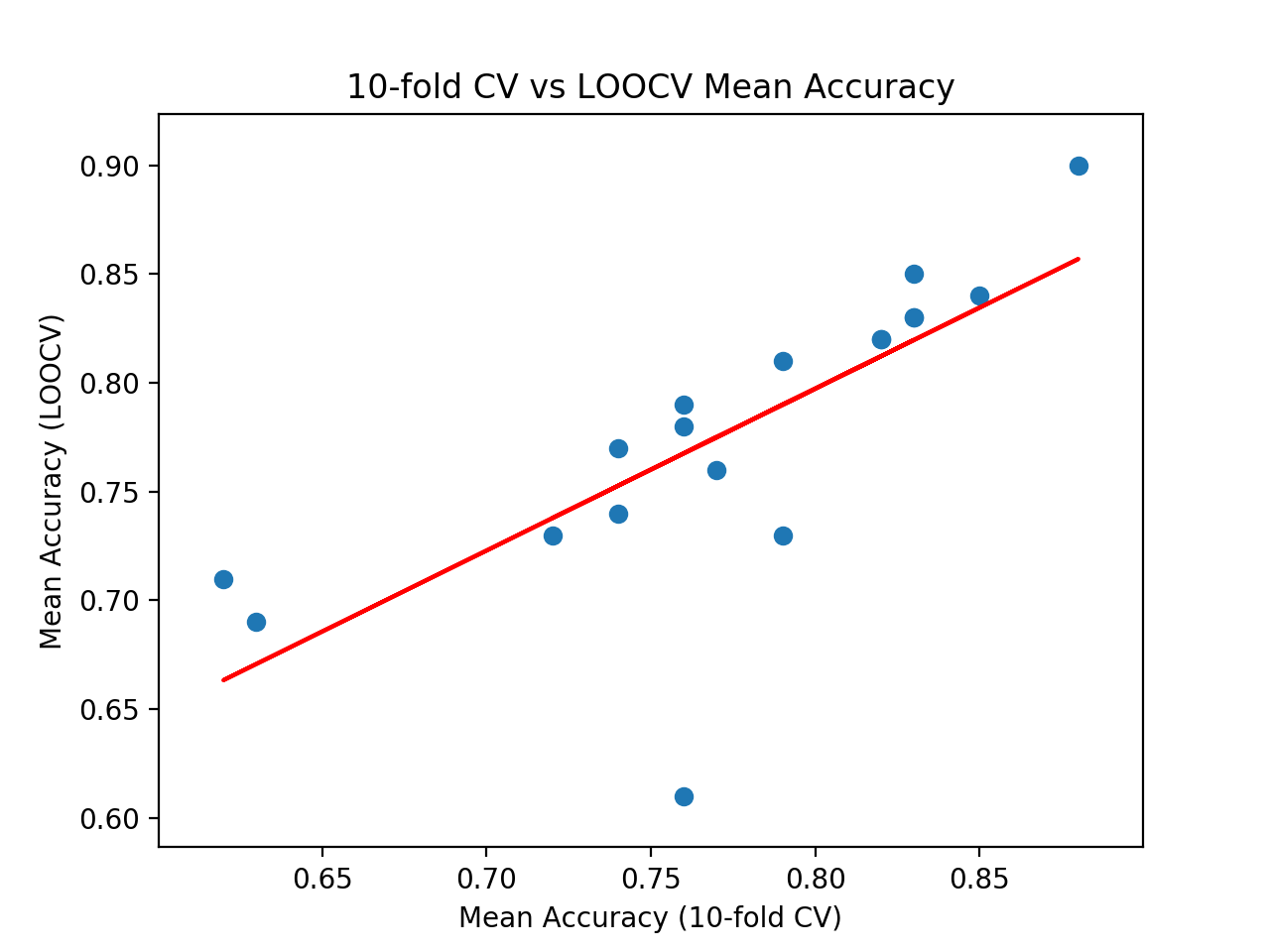
El diagrama de dispersión de la validación cruzada contra la prueba ideal significa la precisión con la línea de mejor ajuste

Esto proporciona un arnés para comparar el arnés de prueba elegido con una condición de prueba ideal en su propio conjunto de datos.