La clasificación desequilibrada son aquellas tareas de predicción en las que la distribución de los ejemplos entre las etiquetas de clase no es igual.
La mayoría de los ejemplos de clasificación desequilibrada se centran en las tareas de clasificación binaria, pero muchos de los instrumentos y técnicas de clasificación desequilibrada también apoyan directamente los problemas de clasificación de múltiples clases.
En este tutorial, descubrirá cómo utilizar las herramientas de clasificación desequilibrada con un conjunto de datos multiclase.
Después de completar este tutorial, lo sabrás:
- Sobre el problema de la predicción de la norma de identificación de cristales desequilibrada de múltiples clases.
- Cómo usar el sobremuestreo de SMOTE para la clasificación desequilibrada de múltiples clases.
- Cómo usar el aprendizaje sensible a los costos para una clasificación multiclase desequilibrada.
Descubre SMOTE, clasificación de una clase, aprendizaje sensible a los costos, movimiento de umbral, y mucho más en mi nuevo libro, con 30 tutoriales paso a paso y código fuente completo en Python.
Empecemos.

Clasificación Desequilibrada de Multi-clase
Foto de istolethetv, algunos derechos reservados.
Resumen del Tutorial
Este tutorial está dividido en tres partes; son:
- Conjunto de datos de clasificación de vidrio de clases múltiples
- Sobremuestreo SMOTE para la clasificación de clases múltiples
- Aprendizaje sensible a los costos para la clasificación de clases múltiples
Conjunto de datos de clasificación de vidrio de clases múltiples
En este tutorial, nos centraremos en el problema de la clasificación estándar desequilibrada de clases múltiples, denominado «Identificación del vidrio«o simplemente»vidrio.”
El conjunto de datos describe las propiedades químicas del vidrio e implica la clasificación de las muestras de vidrio utilizando sus propiedades químicas como una de las seis clases. El conjunto de datos fue acreditado a Vina Spiehler en 1987.
Ignorando el número de identificación de la muestra, hay nueve variables de entrada que resumen las propiedades del conjunto de datos del vidrio; son:
- RI: Índice de refracción
- No: Sodio
- Mg: Magnesio
- Al: Aluminio
- Si: Silicio
- K: Potasio
- Ca: Calcio
- Ba: Bario
- Fe: Hierro
Las composiciones químicas se miden como el porcentaje de peso en el óxido correspondiente.
Hay siete tipos de vidrio en la lista; son:
- Clase 1: construcción de ventanas (procesadas por flotación)
- Clase 2: ventanas de edificios (no procesadas a flote)
- Clase 3: ventanas de vehículos (procesadas por flotación)
- Clase 4: ventanas de vehículos (no procesadas a flote)
- Clase 5: contenedores
- Clase 6: vajilla
- Clase 7: faros
El vidrio flotado se refiere al proceso utilizado para hacer el vidrio.
Hay 214 observaciones en el conjunto de datos y el número de observaciones en cada clase está desequilibrado. Obsérvese que no hay ejemplos para la clase 4 (ventanas de vehículos procesados no flotantes) en el conjunto de datos.
- Clase 1: 70 ejemplos
- Clase 2: 76 ejemplos
- Clase 3: 17 ejemplos
- Clase 4: 0 ejemplos
- Clase 5: 13 ejemplos
- Clase 6: 9 ejemplos
- Clase 7: 29 ejemplos
Aunque hay clases minoritarias, todas las clases son igualmente importantes en este problema de predicción.
El conjunto de datos puede dividirse en vidrio de ventana (clases 1-4) y vidrio no de ventana (clases 5-7). Hay 163 ejemplos de vidrio de ventana y 51 ejemplos de vidrio no de ventana.
- Vidrio de la ventana: 163 ejemplos
- Vidrios sin ventanas: 51 ejemplos
Otra división de las observaciones sería entre el vidrio procesado flotante y el vidrio procesado no flotante, en el caso del vidrio de ventana solamente. Esta división es más equilibrada.
- Vidrio flotante: 87 ejemplos
- Vidrio no flotante: 76 ejemplos
Puedes aprender más sobre el conjunto de datos aquí:
No es necesario descargar el conjunto de datos; lo descargaremos automáticamente como parte de los ejemplos trabajados.
A continuación se muestra una muestra de las primeras filas de los datos.
|
1.52101,13.64,4.49,1.10,71.78,0.06,8.75,0.00,0.00,1 1.51761,13.89,3.60,1.36,72.73,0.48,7.83,0.00,0.00,1 1.51618,13.53,3.55,1.54,72.99,0.39,7.78,0.00,0.00,1 1.51766,13.21,3.69,1.29,72.61,0.57,8.22,0.00,0.00,1 1.51742,13.27,3.62,1.24,73.08,0.55,8.07,0.00,0.00,1 … |
Podemos ver que todas las entradas son numéricas y la variable objetivo en la última columna es la etiqueta de clase codificada entera.
Puedes aprender más sobre cómo trabajar con este conjunto de datos como parte de un proyecto en el tutorial:
Ahora que estamos familiarizados con el conjunto de datos de la clasificación de vidrio multiclase, exploremos cómo podemos usar las herramientas estándar de clasificación desequilibrada con él.
¿Quieres empezar con la clasificación de desequilibrio?
Toma mi curso intensivo gratuito de 7 días por correo electrónico ahora (con código de muestra).
Haga clic para inscribirse y también para obtener una versión gratuita del curso en formato PDF.
Descargue su minicurso GRATUITO
Sobremuestreo SMOTE para la clasificación de clases múltiples
El sobremuestreo se refiere a la copia o síntesis de nuevos ejemplos de las clases minoritarias para que el número de ejemplos en la clase minoritaria se asemeje o coincida mejor con el número de ejemplos en las clases mayoritarias.
Tal vez el enfoque más utilizado para sintetizar nuevos ejemplos es el llamado Synthetic Minority Oversampling TEchnique, o SMOTE para abreviar. Esta técnica fue descrita por Nitesh Chawla, et al. en su artículo de 2002 titulado «SMOTE: Técnica de sobremuestreo de minorías sintéticas».
Puedes aprender más sobre SMOTE en el tutorial:
La biblioteca de aprendizaje desequilibrado proporciona una implementación de SMOTE que podemos utilizar y que es compatible con la popular biblioteca de aprendizaje de ciencias.
Primero, la biblioteca debe ser instalada. Podemos instalarla usando pip de la siguiente manera:
sudo pip instalar desequilibrio-aprender
Podemos confirmar que la instalación se realizó con éxito imprimiendo la versión de la biblioteca instalada:
|
# Revisar el número de versión importación imblearn imprimir(imblearn.La versión…) |
Ejecutando el ejemplo se imprimirá el número de versión de la biblioteca instalada; por ejemplo:
Antes de aplicar SMOTE, carguemos primero el conjunto de datos y confirmemos el número de ejemplos de cada clase.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
# Cargar y resumir el conjunto de datos de pandas importación read_csv de colecciones importación Contador de matplotlib importación pyplot de sklearn.preprocesamiento importación LabelEncoder # Definir la ubicación del conjunto de datos url = ‘https://raw.githubusercontent.com/jbrownlee/Datasets/master/glass.csv’ # Cargar el archivo csv como un marco de datos df = read_csv(url, encabezado=Ninguno) datos = df.valores # Dividido en elementos de entrada y salida X, y = datos[[:, :–1], datos[[:, –1] # La etiqueta codifica la variable objetivo y = LabelEncoder().fit_transform(y) # Resumir la distribución contador = Contador(y) para k,v en contador.artículos(): por = v / len(y) * 100 imprimir(«Clase=%d, n=%d (%.3f%%) % (k, v, por)) # trazar la distribución pyplot.bar(contador.claves(), contador.valores()) pyplot.mostrar() |
Ejecutando el ejemplo primero descarga el conjunto de datos y lo divide en trenes y conjuntos de pruebas.
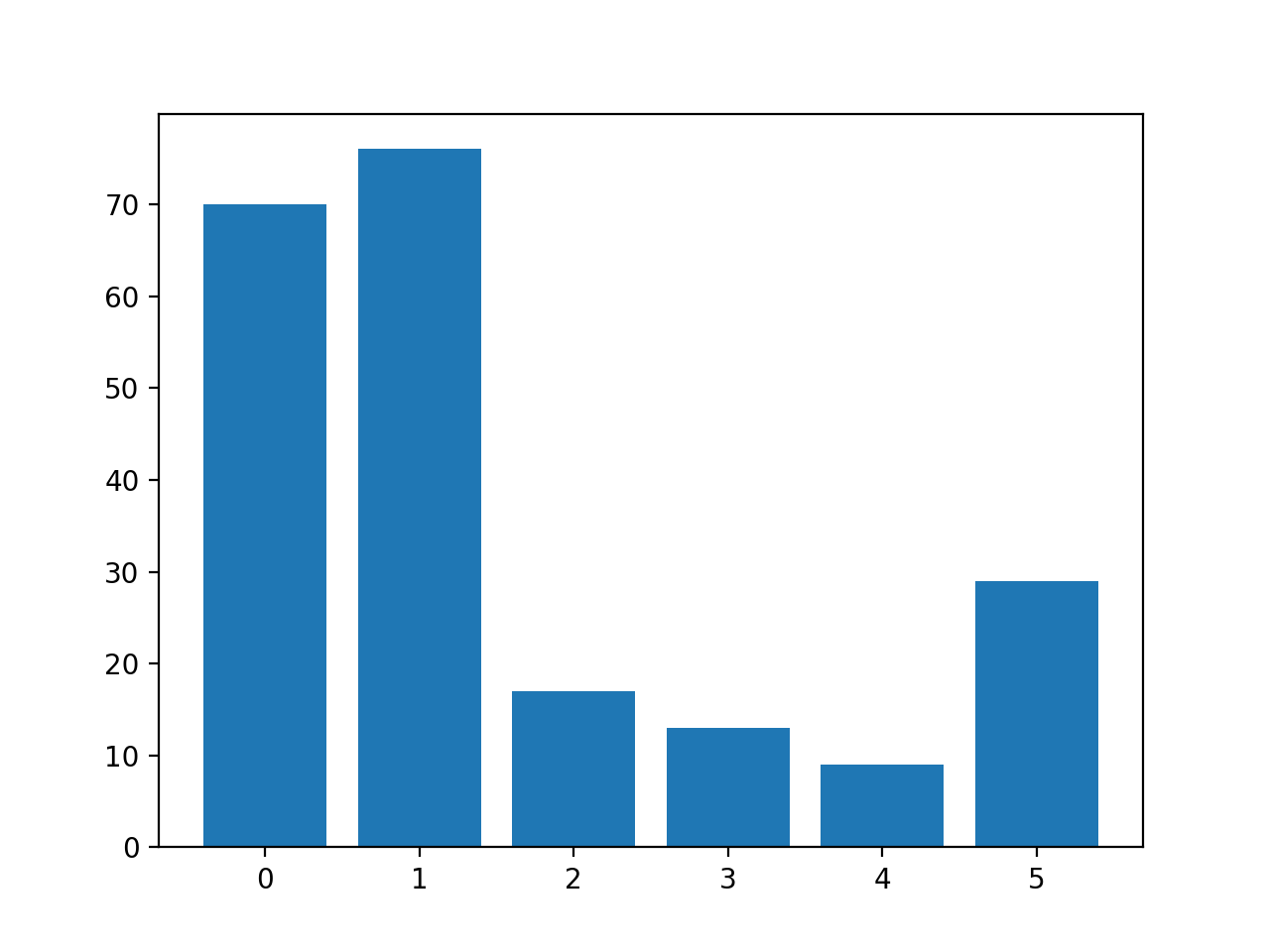
A continuación se informa del número de filas de cada clase, lo que confirma que algunas clases, como la 0 y la 1, tienen muchos más ejemplos (más de 70) que otras clases, como la 3 y la 4 (menos de 15).
|
Clase=0, n=70 (32.710%) Clase=1, n=76 (35.514%) Clase=2, n=17 (7.944%) Clase=3, n=13 (6.075%) Clase=4, n=9 (4.206%) Clase=5, n=29 (13.551%) |
Se crea un gráfico de barras que proporciona una visualización del desglose de clases del conjunto de datos.
Esto da una idea más clara de que las clases 0 y 1 tienen muchos más ejemplos que las clases 2, 3, 4 y 5.

Histograma de ejemplos de cada clase en el conjunto de datos de la clasificación de vidrio multiclase
A continuación, podemos aplicar SMOTE para sobre-muestrear el conjunto de datos.
Por defecto, SMOTE sobre-muestreará todas las clases para tener el mismo número de ejemplos que la clase con más ejemplos.
En este caso, la clase 1 es la que tiene más ejemplos con 76, por lo tanto, SMOTE sobre-muestreará todas las clases para tener 76 ejemplos.
El ejemplo completo de sobremuestreo del conjunto de datos de cristal con SMOTE se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
# Ejemplo de sobremuestreo de un conjunto de datos de clasificación multiclase de pandas importación read_csv de imblearn.sobre_muestreo importación SMOTE de colecciones importación Contador de matplotlib importación pyplot de sklearn.preprocesamiento importación LabelEncoder # Definir la ubicación del conjunto de datos url = ‘https://raw.githubusercontent.com/jbrownlee/Datasets/master/glass.csv’ # Cargar el archivo csv como un marco de datos df = read_csv(url, encabezado=Ninguno) datos = df.valores # Dividido en elementos de entrada y salida X, y = datos[[:, :–1], datos[[:, –1] # La etiqueta codifica la variable objetivo y = LabelEncoder().fit_transform(y) # Transformar el conjunto de datos Sobremuestreo = SMOTE() X, y = Sobremuestreo.fit_resample(X, y) # Resumir la distribución contador = Contador(y) para k,v en contador.artículos(): por = v / len(y) * 100 imprimir(«Clase=%d, n=%d (%.3f%%) % (k, v, por)) # trazar la distribución pyplot.bar(contador.claves(), contador.valores()) pyplot.mostrar() |
Al ejecutar el ejemplo primero se carga el conjunto de datos y se le aplica SMOTE.
A continuación se informa de la distribución de los ejemplos en cada clase, confirmando que cada clase tiene ahora 76 ejemplos, como esperábamos.
|
Clase=0, n=76 (16.667%) Clase=1, n=76 (16.667%) Clase=2, n=76 (16.667%) Clase=3, n=76 (16.667%) Clase=4, n=76 (16.667%) Clase=5, n=76 (16.667%) |
También se crea un gráfico de barras de la distribución de las clases, que proporciona una fuerte indicación visual de que todas las clases tienen ahora el mismo número de ejemplos.
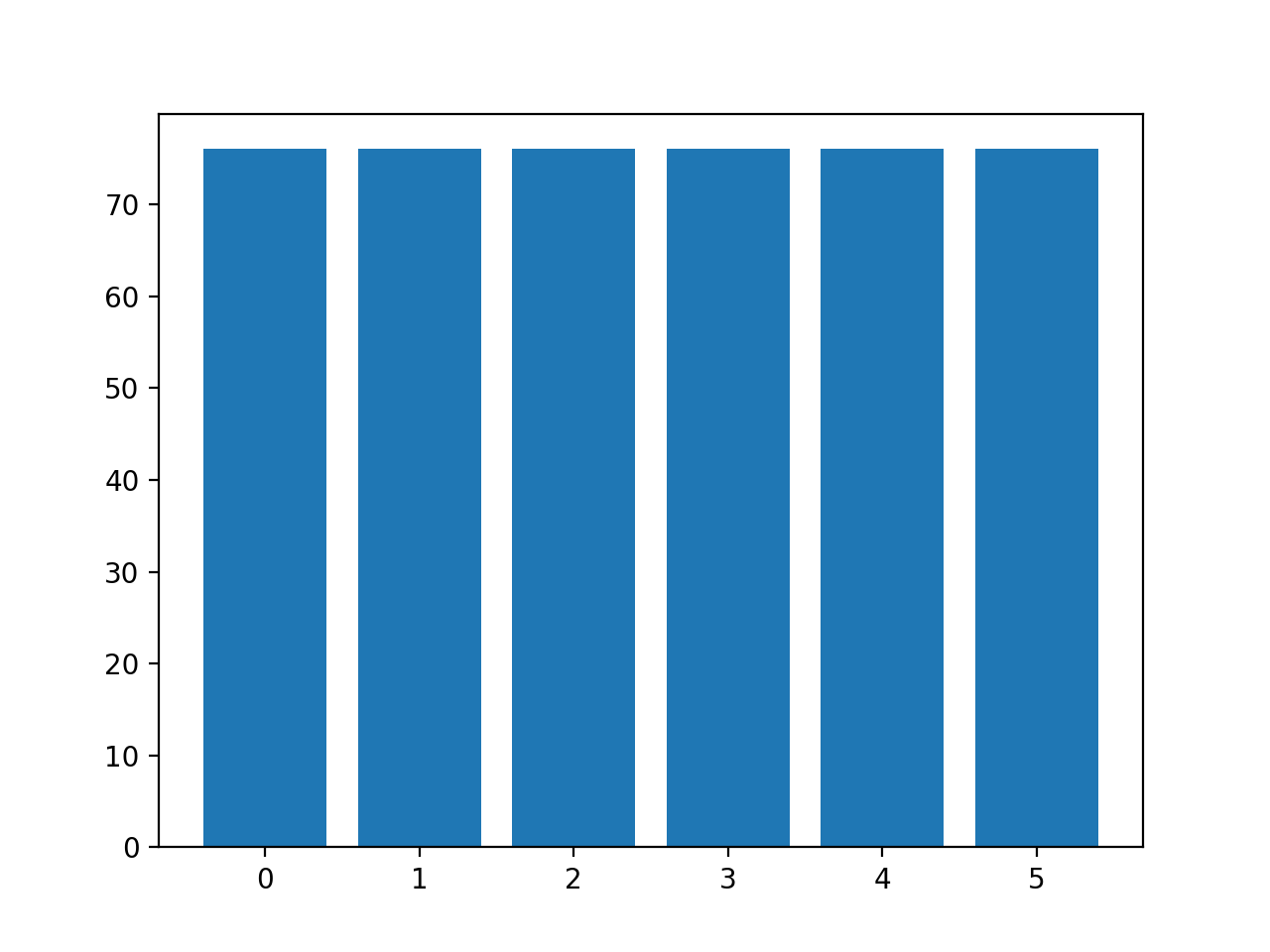
Histograma de ejemplos de cada clase en el conjunto de datos de la clasificación multiclase de vidrio después del sobremuestreo por defecto SMOTE
En lugar de utilizar la estrategia por defecto de SMOTE para sobremuestrear todas las clases hasta el número de ejemplos de la clase mayoritaria, podríamos en cambio especificar el número de ejemplos a sobremuestrear en cada clase.
Por ejemplo, podríamos sobre-muestrear hasta 100 ejemplos en las clases 0 y 1 y 200 ejemplos en las clases restantes. Esto puede lograrse creando un diccionario que asigne las etiquetas de clase al número de ejemplos deseados en cada clase, y luego especificándolo mediante el «estrategia_de_muestreo«argumento a la clase de SMOTE.
|
... # Transformar el conjunto de datos estrategia = {0:100, 1:100, 2:200, 3:200, 4:200, 5:200} Sobremuestreo = SMOTE(estrategia_de_muestreo=estrategia) X, y = Sobremuestreo.fit_resample(X, y) |
Enlazando todo esto, el ejemplo completo de la utilización de una estrategia de sobremuestreo personalizada para el SMOTE se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
# Ejemplo de sobremuestreo de un conjunto de datos de clasificación multiclase con una estrategia personalizada de pandas importación read_csv de imblearn.sobre_muestreo importación SMOTE de colecciones importación Contador de matplotlib importación pyplot de sklearn.preprocesamiento importación LabelEncoder # Definir la ubicación del conjunto de datos url = ‘https://raw.githubusercontent.com/jbrownlee/Datasets/master/glass.csv’ # Cargar el archivo csv como un marco de datos df = read_csv(url, encabezado=Ninguno) datos = df.valores # Dividido en elementos de entrada y salida X, y = datos[[:, :–1], datos[[:, –1] # La etiqueta codifica la variable objetivo y = LabelEncoder().fit_transform(y) # Transformar el conjunto de datos estrategia = {0:100, 1:100, 2:200, 3:200, 4:200, 5:200} Sobremuestreo = SMOTE(estrategia_de_muestreo=estrategia) X, y = Sobremuestreo.fit_resample(X, y) # Resumir la distribución contador = Contador(y) para k,v en contador.artículos(): por = v / len(y) * 100 imprimir(«Clase=%d, n=%d (%.3f%%) % (k, v, por)) # trazar la distribución pyplot.bar(contador.claves(), contador.valores()) pyplot.mostrar() |
La ejecución del ejemplo crea el muestreo deseado y resume el efecto en el conjunto de datos, confirmando el resultado deseado.
|
Clase=0, n=100 (10.000%) Clase=1, n=100 (10.000%) Clase=2, n=200 (20.000%) Clase=3, n=200 (20.000%) Clase=4, n=200 (20.000%) Clase=5, n=200 (20.000%) |
Nota: puede ver advertencias que pueden ser ignoradas con seguridad para los propósitos de este ejemplo, como:
|
UserWarning: Después del sobre-muestreo, el número de muestras (200) en la clase 5 será mayor que el número de muestras en la clase mayoritaria (clase #1 -> 76) |
También se crea un gráfico de barras de la distribución de clases que confirma la distribución de clases especificada tras el muestreo de los datos.
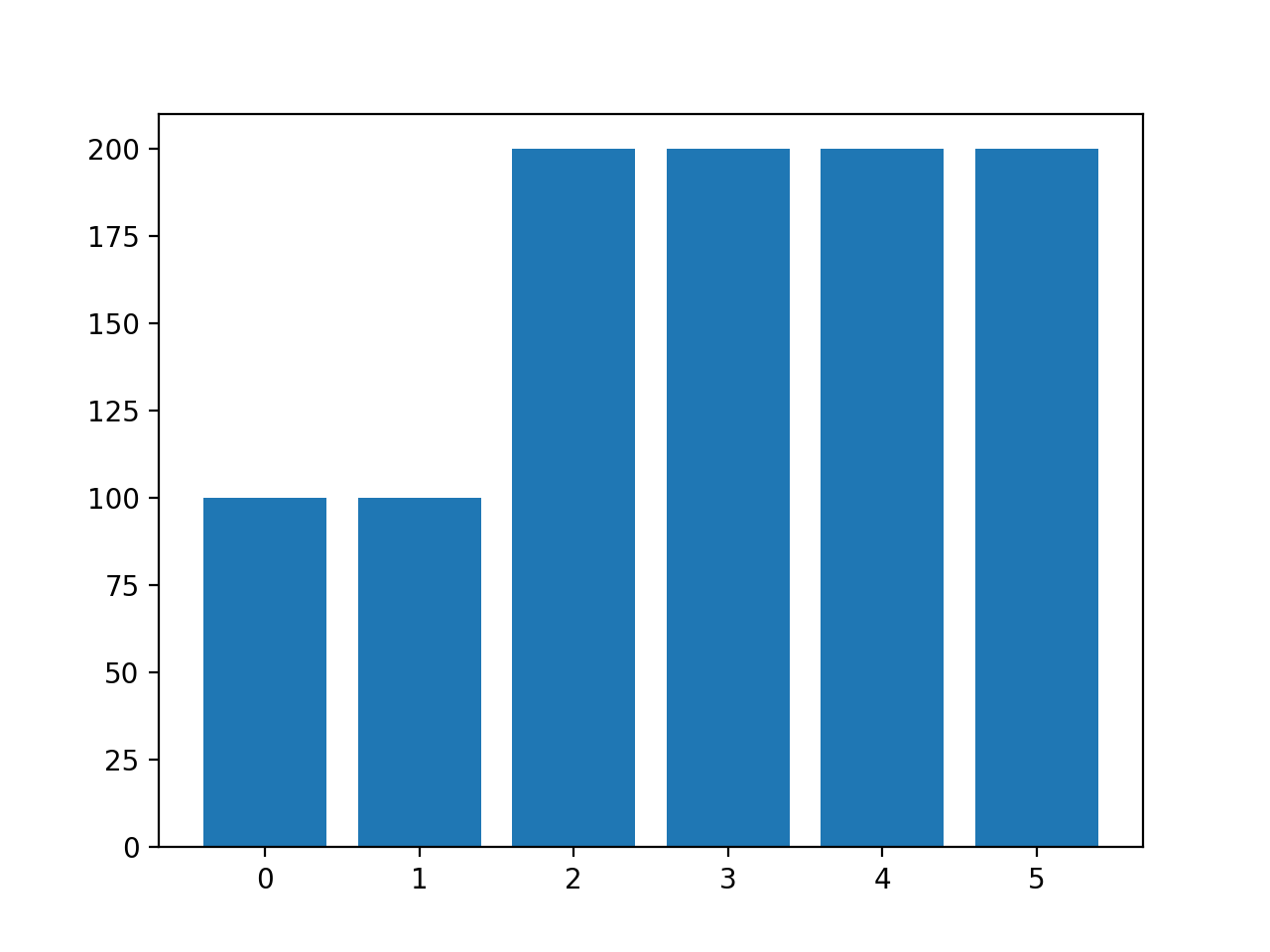
Histograma de ejemplos de cada clase en el conjunto de datos de la clasificación de vidrio multiclase después del sobremuestreo personalizado SMOTE
NotaCuando se utiliza un muestreo de datos como el SMOTE, sólo debe aplicarse al conjunto de datos de entrenamiento, no al conjunto de datos completo. Recomiendo usar un Pipeline para asegurar que el método SMOTE se use correctamente cuando se evalúen los modelos y se hagan predicciones con ellos.
Puedes ver un ejemplo del uso correcto de SMOTE en un Pipeline en este tutorial:
Aprendizaje sensible a los costos para la clasificación de clases múltiples
La mayoría de los algoritmos de aprendizaje de máquinas asumen que todas las clases tienen un número igual de ejemplos.
Este no es el caso de la clasificación desequilibrada de clases múltiples. Los algoritmos pueden modificarse para cambiar la forma en que se realiza el aprendizaje y sesgarlo hacia las clases que tienen menos ejemplos en el conjunto de datos de formación. Esto se denomina generalmente aprendizaje sensible a los costos.
Para obtener más información sobre el aprendizaje sensible a los costos, vea el tutorial:
La clase de RandomForestClassifier en scikit-learn apoya el aprendizaje sensible a los costos a través de la «peso_de_clase«argumento».
Por defecto, la clase de bosque aleatorio asigna el mismo peso a cada clase.
Podemos evaluar la precisión de la clasificación de la ponderación de la clase de bosque aleatoria predeterminada en el conjunto de datos de la clasificación multiclase desequilibrada de cristal.
El ejemplo completo figura a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
# Modelo base y arnés de prueba para el conjunto de datos de identificación del cristal de numpy importación significa de numpy importación std de pandas importación read_csv de sklearn.preprocesamiento importación LabelEncoder de sklearn.model_selection importación puntaje_valor_cruzado de sklearn.model_selection importación RepeatedStratifiedKFold de sklearn.conjunto importación RandomForestClassifier # Cargar el conjunto de datos def load_dataset(camino_completo): # Cargar el conjunto de datos como una matriz numérica datos = read_csv(camino_completo, encabezado=Ninguno) # Recuperar la matriz numérica datos = datos.valores # Dividido en elementos de entrada y salida X, y = datos[[:, :–1], datos[[:, –1] # La etiqueta codifica la variable objetivo para que las clases 0 y 1 y = LabelEncoder().fit_transform(y) volver X, y # Evaluar un modelo def evaluate_model(X, y, modelo): # Definir el procedimiento de evaluación cv = RepeatedStratifiedKFold(n_splits=5, n_repeticiones=3, estado_aleatorio=1) # Evaluar el modelo resultados = puntaje_valor_cruzado(modelo, X, y, puntuación=«exactitud, cv=cv, n_jobs=–1) volver resultados # Definir la ubicación del conjunto de datos camino_completo = ‘https://raw.githubusercontent.com/jbrownlee/Datasets/master/glass.csv’ # Cargar el conjunto de datos X, y = load_dataset(camino_completo) # Definir el modelo de referencia modelo = RandomForestClassifier(n_estimadores=1000) # Evaluar el modelo resultados = evaluate_model(X, y, modelo) # Resumir el rendimiento imprimir(«Precisión media: %.3f (%.3f) % (significa(resultados), std(resultados))) |
La ejecución del ejemplo evalúa el algoritmo de bosque aleatorio predeterminado con 1.000 árboles en el conjunto de datos de cristal utilizando una validación cruzada repetida estratificada en k.
La precisión de la clasificación de la media y la desviación estándar se informa al final del recorrido.
Sus resultados específicos pueden variar dada la naturaleza estocástica del algoritmo de aprendizaje, el procedimiento de evaluación y las diferencias de precisión entre las máquinas. Intenta ejecutar el ejemplo unas cuantas veces.
En este caso, podemos ver que el modelo por defecto alcanzó una precisión de clasificación de alrededor del 79,6 por ciento.
|
Precisión media: 0,796 (0,047) |
Podemos especificar el «peso_de_clase«argumento al valor»equilibrado«que calcula automáticamente una ponderación de clase que asegurará que cada clase reciba una ponderación igual durante el entrenamiento del modelo.
|
... # Definir el modelo modelo = RandomForestClassifier(n_estimadores=1000, peso_de_clase=«equilibrado) |
A continuación se muestra el ejemplo completo.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
# Bosque aleatorio sensible al costo con pesos de clase predeterminados de numpy importación significa de numpy importación std de pandas importación read_csv de sklearn.preprocesamiento importación LabelEncoder de sklearn.model_selection importación puntaje_valor_cruzado de sklearn.model_selection importación RepeatedStratifiedKFold de sklearn.conjunto importación RandomForestClassifier # Cargar el conjunto de datos def load_dataset(camino_completo): # Cargar el conjunto de datos como una matriz numérica datos = read_csv(camino_completo, encabezado=Ninguno) # Recuperar la matriz numérica datos = datos.valores # Dividido en elementos de entrada y salida X, y = datos[[:, :–1], datos[[:, –1] # La etiqueta codifica la variable objetivo y = LabelEncoder().fit_transform(y) volver X, y # Evaluar un modelo def evaluate_model(X, y, modelo): # Definir el procedimiento de evaluación cv = RepeatedStratifiedKFold(n_splits=5, n_repeticiones=3, estado_aleatorio=1) # Evaluar el modelo resultados = puntaje_valor_cruzado(modelo, X, y, puntuación=«exactitud, cv=cv, n_jobs=–1) volver resultados # Definir la ubicación del conjunto de datos camino_completo = ‘https://raw.githubusercontent.com/jbrownlee/Datasets/master/glass.csv’ # Cargar el conjunto de datos X, y = load_dataset(camino_completo) # Definir el modelo modelo = RandomForestClassifier(n_estimadores=1000, peso_de_clase=«equilibrado) # Evaluar el modelo resultados = evaluate_model(X, y, modelo) # Resumir el rendimiento imprimir(«Precisión media: %.3f (%.3f) % (significa(resultados), std(resultados))) |
El ejemplo informa de la precisión de la clasificación de la media y la desviación estándar de la versión de bosque aleatorio sensible al coste en el conjunto de datos de cristal.
Sus resultados específicos pueden variar dada la naturaleza estocástica del algoritmo de aprendizaje, el procedimiento de evaluación y las diferencias de precisión entre las máquinas. Intenta ejecutar el ejemplo unas cuantas veces.
En este caso, podemos ver que el modelo por defecto logró un aumento en la precisión de la clasificación con respecto a la versión del algoritmo que no es sensible a los costos, con una precisión de clasificación del 80,2 por ciento frente al 79,6 por ciento.
|
Precisión media: 0,802 (0,044) |
El «peso_de_claseEl argumento «toma un diccionario de etiquetas de clase mapeadas a un valor de ponderación de clase».
Podemos usar esto para especificar una ponderación personalizada, como una ponderación por defecto para las clases 0 y 1.0 que tienen muchos ejemplos y una ponderación de clase doble de 2.0 para las otras clases.
|
... # Definir el modelo pesos = {0:1.0, 1:1.0, 2:2.0, 3:2.0, 4:2.0, 5:2.0} modelo = RandomForestClassifier(n_estimadores=1000, peso_de_clase=pesos) |
Enlazando todo esto, a continuación se enumera el ejemplo completo de la utilización de una ponderación de clase personalizada para el aprendizaje sensible a los costos en el problema de la clasificación desequilibrada de clases múltiples de vidrio.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
# Bosque aleatorio sensible al costo con ponderaciones de clases personalizadas de numpy importación significa de numpy importación std de pandas importación read_csv de sklearn.preprocesamiento importación LabelEncoder de sklearn.model_selection importación puntaje_valor_cruzado de sklearn.model_selection importación RepeatedStratifiedKFold de sklearn.conjunto importación RandomForestClassifier # Cargar el conjunto de datos def load_dataset(camino_completo): # Cargar el conjunto de datos como una matriz numérica datos = read_csv(camino_completo, encabezado=Ninguno) # Recuperar la matriz numérica datos = datos.valores # Dividido en elementos de entrada y salida X, y = datos[[:, :–1], datos[[:, –1] # La etiqueta codifica la variable objetivo y = LabelEncoder().fit_transform(y) volver X, y # Evaluar un modelo def evaluate_model(X, y, modelo): # Definir el procedimiento de evaluación cv = RepeatedStratifiedKFold(n_splits=5, n_repeticiones=3, estado_aleatorio=1) # Evaluar el modelo resultados = puntaje_valor_cruzado(modelo, X, y, puntuación=«exactitud, cv=cv, n_jobs=–1) volver resultados # Definir la ubicación del conjunto de datos camino_completo = ‘https://raw.githubusercontent.com/jbrownlee/Datasets/master/glass.csv’ # Cargar el conjunto de datos X, y = load_dataset(camino_completo) # Definir el modelo pesos = {0:1.0, 1:1.0, 2:2.0, 3:2.0, 4:2.0, 5:2.0} modelo = RandomForestClassifier(n_estimadores=1000, peso_de_clase=pesos) # Evaluar el modelo resultados = evaluate_model(X, y, modelo) # Resumir el rendimiento imprimir(«Precisión media: %.3f (%.3f) % (significa(resultados), std(resultados))) |
El ejemplo informa de la precisión de la clasificación de la media y la desviación estándar de la versión de bosque aleatorio sensible a los costes en el conjunto de datos de cristal con pesos personalizados.
Sus resultados específicos pueden variar dada la naturaleza estocástica del algoritmo de aprendizaje, el procedimiento de evaluación y las diferencias de precisión entre las máquinas. Intenta ejecutar el ejemplo unas cuantas veces.
En este caso, podemos ver que logramos un mayor aumento de la precisión desde alrededor del 80,2 por ciento con una ponderación de clase equilibrada hasta el 80,8 por ciento con una ponderación de clase más sesgada.
|
Precisión media: 0,808 (0,059) |
