Cálculo en el aprendizaje automático: por qué funciona

Tal función lineal se puede representar mediante la ecuación de una línea que tiene una pendiente, metro, y una intersección con el eje y, C:

y = mx + C

Variando cada uno de los parámetros, metro y C, produce diferentes modelos lineales que definen diferentes asignaciones de entrada-salida.

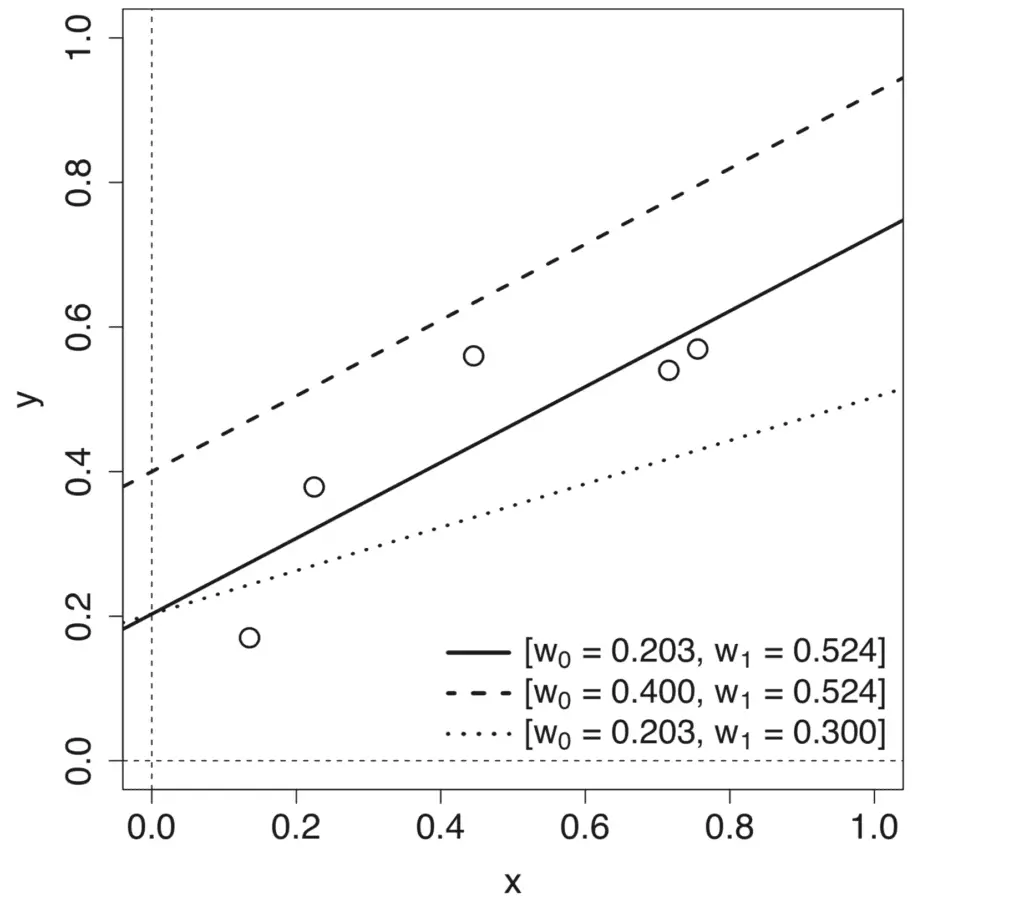
Gráfico de línea de diferentes modelos de línea producidos variando la pendiente y la intersección
Tomado de Deep Learning

El proceso de aprendizaje de la función de mapeo, por lo tanto, implica la aproximación de estos parámetros del modelo, o pesos, que dan como resultado el error mínimo entre las salidas previstas y las previstas. Este error se calcula por medio de una función de pérdida, función de costo o función de error, como se usa indistintamente, y el proceso de minimizar la pérdida se conoce como optimización de funciones.

Podemos aplicar el cálculo diferencial al proceso de optimización de funciones.

Para comprender mejor cómo se puede aplicar el cálculo diferencial a la optimización de funciones, volvamos a nuestro ejemplo específico de tener una función de mapeo lineal.

Digamos que tenemos un conjunto de datos de características de entrada única, X, y sus correspondientes productos objetivo, y. Para medir el error en el conjunto de datos, tomaremos la suma de los errores al cuadrado (SSE), calculada entre las salidas previstas y objetivo, como nuestra función de pérdida.

Llevando a cabo un barrido de parámetros a través de diferentes valores para los pesos del modelo, w₀ = metro y w₁ = C, genera perfiles de error individuales de forma convexa.

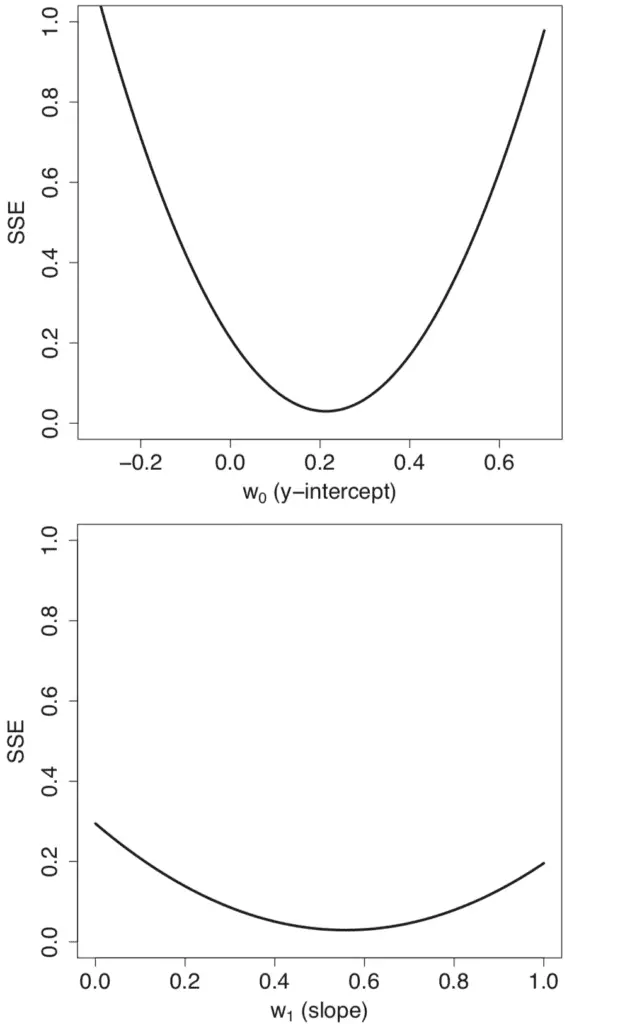
Perfiles de gráficos de línea de error (SSE) generados al realizar un barrido en un rango de valores para la pendiente y la intersección
Tomado de Deep Learning

La combinación de los perfiles de error individuales genera una superficie de error tridimensional que también tiene forma convexa. Esta superficie de error está contenida dentro de un espacio de peso, que está definido por los rangos de valores de barrido para los pesos del modelo, w₀ y w₁.

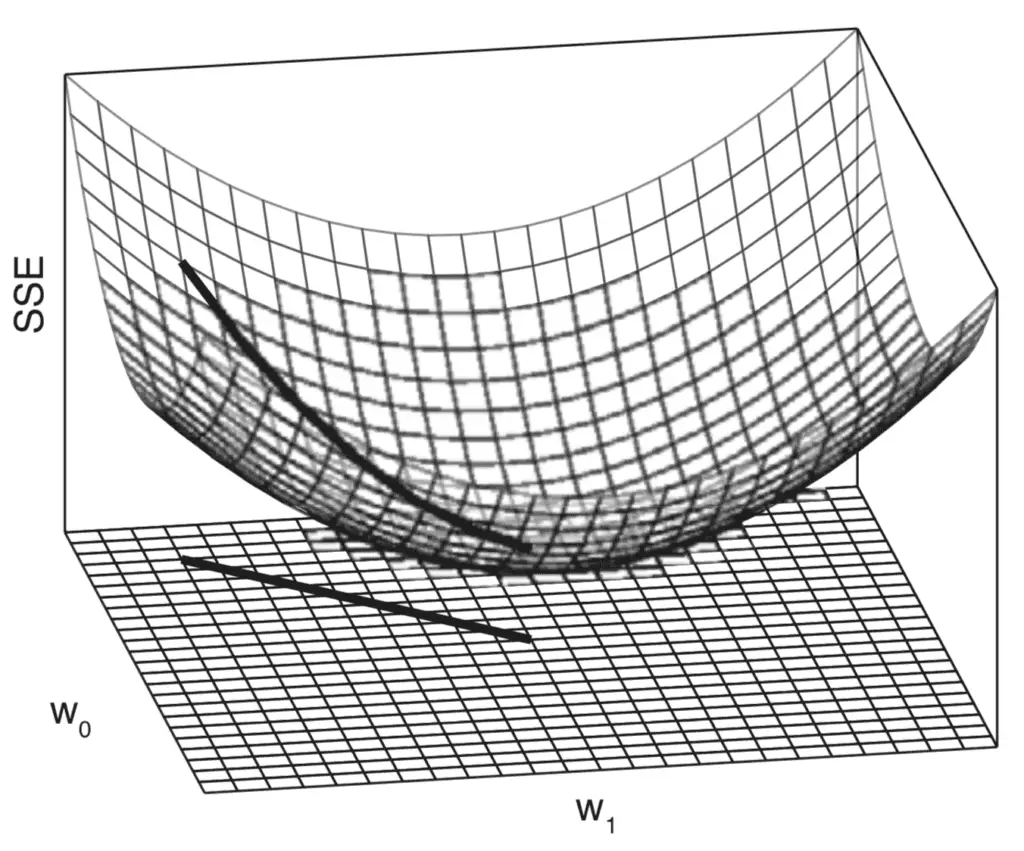
Gráfico tridimensional de la superficie de error (SSE) generada cuando se varían tanto la pendiente como la intersección
Tomado de Deep Learning

Moverse a través de este espacio de peso es equivalente a moverse entre diferentes modelos lineales. Nuestro objetivo es identificar el modelo que mejor se ajusta a los datos entre todas las alternativas posibles. El mejor modelo se caracteriza por el error más bajo en el conjunto de datos, que se corresponde con el punto más bajo en la superficie del error.

Una superficie de error convexa o en forma de cuenco es increíblemente útil para aprender una función lineal para modelar un conjunto de datos porque significa que el proceso de aprendizaje puede enmarcarse como una búsqueda del punto más bajo en la superficie de error. El algoritmo estándar utilizado para encontrar este punto más bajo se conoce como descenso de gradiente.

Página 194, Deep Learning, 2019.

El algoritmo de descenso de gradiente, como el algoritmo de optimización, buscará alcanzar el punto más bajo en la superficie de error siguiendo su gradiente cuesta abajo. Este descenso se basa en el cálculo del gradiente o pendiente de la superficie de error.

Recomendado:  5 famosos desastres analíticos y de IA

Aquí es donde entra en juego el cálculo diferencial.

El cálculo, y en particular la diferenciación, es el campo de las matemáticas que se ocupa de las tasas de cambio.

Página 198, Deep Learning, 2019.

Más formalmente, denotemos la función que nos gustaría optimizar mediante:

error = F(pesos)

Al calcular la tasa de cambio, o la pendiente, del error con respecto a los pesos, el algoritmo de descenso de gradiente puede decidir cómo cambiar los pesos para seguir reduciendo el error.

Por qué funciona el cálculo en el aprendizaje automático

La función de error que hemos considerado optimizar es relativamente simple, porque es convexa y se caracteriza por un único mínimo global.

No obstante, en el contexto del aprendizaje automático, a menudo necesitamos optimizar funciones más complejas que pueden hacer que la tarea de optimización sea muy desafiante. La optimización puede volverse aún más desafiante si la entrada a la función también es multidimensional.

El cálculo nos proporciona las herramientas necesarias para abordar ambos desafíos.

Supongamos que tenemos una función más genérica que deseamos minimizar y que toma una entrada real, X, para producir una salida real, y:

y = f (X)

Calcular la tasa de cambio a diferentes valores de X es útil porque nos da una indicación de los cambios que debemos aplicar a X, con el fin de obtener los cambios correspondientes en y.

Dado que estamos minimizando la función, nuestro objetivo es llegar a un punto que obtenga un valor tan bajo de f (X) como sea posible que también se caracteriza por una tasa de cambio cero; por lo tanto, un mínimo global. Dependiendo de la complejidad de la función, esto puede no ser necesariamente posible ya que puede haber muchos mínimos locales o puntos de silla en los que el algoritmo de optimización puede quedar atrapado.

En el contexto del aprendizaje profundo, optimizamos funciones que pueden tener muchos mínimos locales que no son óptimos y muchos puntos de silla rodeados por regiones muy planas.

Página 84, Deep Learning, 2017.

Por lo tanto, dentro del contexto del aprendizaje profundo, a menudo aceptamos una solución subóptima que puede no corresponder necesariamente a un mínimo global, siempre que corresponda a un valor muy bajo de f (X).

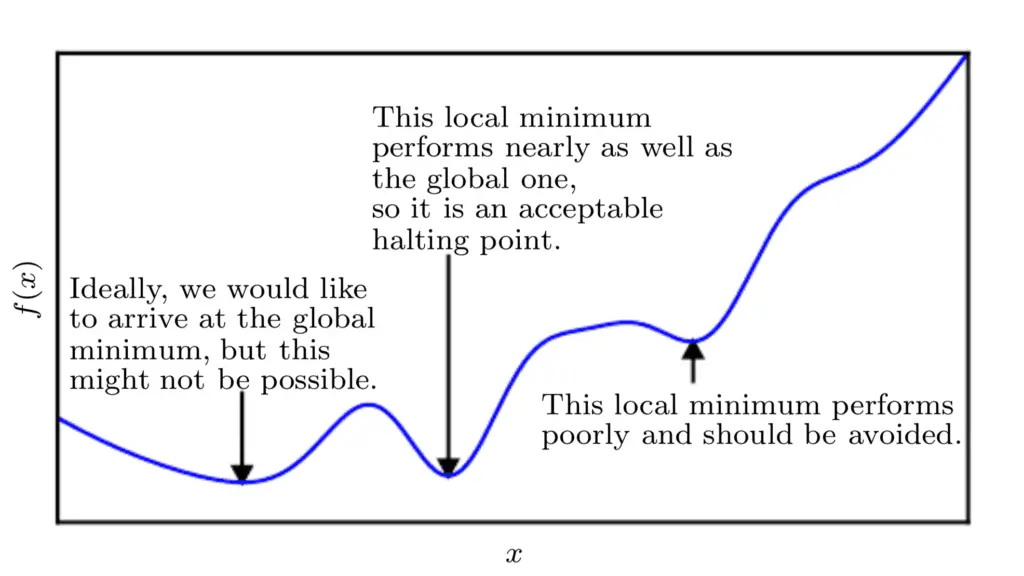
Gráfico de línea de la función de costo para minimizar la visualización de mínimos locales y globales
Tomado de Deep Learning

Si la función con la que estamos trabajando toma múltiples entradas, el cálculo también nos proporciona el concepto de Derivadas parciales; o en términos más simples, un método para calcular la tasa de cambio de y con respecto a cambios en cada una de las entradas, X_I, mientras se mantienen constantes las entradas restantes.

Es por eso que cada uno de los pesos se actualiza de forma independiente en el algoritmo de descenso de gradiente: la regla de actualización de peso depende de la derivada parcial del SSE para cada peso, y debido a que hay una derivada parcial diferente para cada peso, hay un peso separado actualizar la regla para cada peso.

Página 200, Deep Learning, 2019.

Por lo tanto, si consideramos nuevamente la minimización de una función de error, calcular la derivada parcial del error con respecto a cada peso específico permite que cada peso se actualice independientemente de los demás.

Recomendado:  Mercado de inteligencia artificial y aprendizaje automático 2022 Tecnologías de tendencia, planes de desarrollo, crecimiento futuro y regiones geográficas hasta 2028

Esto también significa que es posible que el algoritmo de descenso de gradiente no siga una trayectoria recta por la superficie del error. Más bien, cada ponderación se actualizará en proporción al gradiente local de la curva de error. Por lo tanto, un peso puede actualizarse en una cantidad mayor que otro, tanto como sea necesario para que el algoritmo de descenso de gradiente alcance el mínimo de la función.

Otras lecturas

Esta sección proporciona más recursos sobre el tema si desea profundizar.

Libros

Resumen

En este tutorial, descubrió el papel integral del cálculo en el aprendizaje automático.

Específicamente, aprendiste:

• El cálculo juega un papel integral en la comprensión del funcionamiento interno de los algoritmos de aprendizaje automático, como el algoritmo de descenso de gradiente que minimiza una función de error basada en el cálculo de la tasa de cambio.
• El concepto de la tasa de cambio en el cálculo también se puede explotar para minimizar funciones objetivas más complejas que no son necesariamente de forma convexa.
• El cálculo de la derivada parcial, otro concepto importante en cálculo, nos permite trabajar con funciones que toman múltiples entradas.

¿Tiene usted alguna pregunta?
Haga sus preguntas en los comentarios a continuación y haré todo lo posible para responder.