Esta entrada está en la lista cruzada del blog de la CMU ML.
La historia del aprendizaje de las máquinas ha sido en gran medida una historia de aumento
abstracción. En los albores de la ML, los investigadores dedicaron un esfuerzo considerable
características de ingeniería. A medida que el aprendizaje profundo ganaba popularidad, los investigadores
se dirigió hacia el ajuste de las reglas de actualización y las tasas de aprendizaje para su
optimizadores. La reciente investigación en el meta-aprendizaje ha subido un nivel de
abstracción superior: muchos investigadores ahora pasan sus días construyendo manualmente
distribuciones de tareas, de las cuales pueden aprender automáticamente buenos optimizadores.
¿Cuál podría ser el siguiente peldaño de esta escalera? En este post introducimos la teoría
y algoritmos para meta-aprendizaje no supervisadodonde el aprendizaje de la máquina
los propios algoritmos proponen sus propias distribuciones de tareas. Sin supervisión
El meta-aprendizaje reduce aún más la cantidad de supervisión humana necesaria para resolver
tareas, potencialmente insertando un nuevo peldaño en esta escalera de la abstracción.
Empezamos discutiendo cómo los algoritmos de aprendizaje de las máquinas usan la supervisión humana para
encontrar patrones y extraer conocimientos de los datos observados. La máquina más común
El entorno de aprendizaje es regresióndonde un humano proporciona etiquetas de $Y$ para un conjunto de
ejemplos $X$. El objetivo es devolver un predictor que asigne correctamente
etiquetas a ejemplos novedosos. Otro problema común de aprendizaje de la máquina es
aprendizaje de refuerzo (RL)donde un agente toma acciones en un ambiente.
En RL, los humanos indican el comportamiento deseado a través de una función de recompensa que
el agente busca maximizar. Para dibujar una cruda analogía con la regresión,
la dinámica del ambiente son los ejemplos $X$, y la función de recompensa da
las etiquetas $Y$. Los algoritmos de regresión y RL emplean muchas herramientas,
incluyendo métodos tabulares (por ejemplo, iteración de valores), métodos lineales (por ejemplo, lineal
regresión) métodos del núcleo (por ejemplo, RBF-SVM), y redes neuronales profundas. A grandes rasgos, los llamamos
algoritmos procedimientos de aprendizaje: procesos que toman como entrada un conjunto de datos
(ejemplos con etiquetas, o transiciones con recompensas) y producir una función que
se desempeña bien (logra una gran precisión o una gran recompensa) en el conjunto de datos.

La investigación de aprendizaje de máquinas es similar a la sala de control de la física grande
experimentos. Los investigadores tienen un número de perillas que pueden afinar que afectan a la
la realización del procedimiento de aprendizaje. El ajuste correcto de las perillas depende
en el experimento en particular: algunos escenarios funcionan bien para la alta energía
otros funcionan bien para experimentos con átomos ultracongelados.
Crédito de la figura.
Similar a los procedimientos de laboratorio utilizados en la física y la biología, el aprendizaje
los procedimientos utilizados en el aprendizaje de la máquina tienen muchas perillas que puede ser afinado.
Por ejemplo, el procedimiento de aprendizaje para entrenar una red neuronal podría ser definido por un optimizador
(por ejemplo, Nesterov, Adam) y una tasa de aprendizaje (por ejemplo, 1e-5).
En comparación con la regresión, los procedimientos de aprendizaje específicos de la RL (por ejemplo, DDPG) a menudo tienen muchos más botones, incluyendo
la frecuencia de la recopilación de datos y la frecuencia con que se actualiza la política.
Encontrar el ajuste correcto para los mandos puede tener un gran efecto en la rapidez
el procedimiento de aprendizaje resuelve una tarea, y una buena configuración de perillas para una
El procedimiento de aprendizaje puede ser una mala configuración para otro.
Mientras que los practicantes de aprendizaje de máquinas a menudo afinan cuidadosamente estas perillas a mano,
si vamos a resolver muchas tareas, puede ser útil automatizar esto
proceso. El proceso de establecer los mandos de los procedimientos de aprendizaje a través de
La optimización se llama meta-aprendizaje [Thrun 1998]. Los algoritmos que realizan esta optimización
problema automáticamente se conocen como algoritmos de meta-aprendizaje.
Afinar explícitamente las perillas de los procedimientos de aprendizaje es un área activa de investigación, con varios investigadores buscando afinar las reglas de actualización [Andrychowicz 2016, Duan 2016, Wang 2016], inicialización del peso [Finn 2017], pesos de la red [Ha 2016]…arquitecturas de red… [Gaier 2019]y otras facetas de los procedimientos de aprendizaje.
Para evaluar un ajuste de perillas, los algoritmos de meta-aprendizaje no consideran una sola tarea
sino una distribución en muchas tareas. Por ejemplo, una distribución sobre las tareas supervisadas
Las tareas de aprendizaje pueden incluir el aprendizaje de un detector de perros, el aprendizaje de un detector de gatos,
y aprender un detector de aves. En el aprendizaje de refuerzo, una distribución de tareas
podría definirse como la conducción de un coche de una manera suave, segura y eficiente,
donde las tareas difieren por el peso que le dan a la suavidad, seguridad y
eficiencia. Idealmente, la distribución de tareas está diseñada para reflejar la
distribución de las tareas que es probable que encontremos en el mundo real.
Dado que las tareas en una distribución de tareas están típicamente relacionadas, la información de
una tarea puede ser útil para resolver otras tareas de manera más eficiente. Como puede ser que
Como es de esperar, un ajuste de la perilla que funciona mejor en una distribución de tareas puede no ser
lo mejor para otra distribución de tareas; el ajuste óptimo de la perilla
depende de la distribución de las tareas.
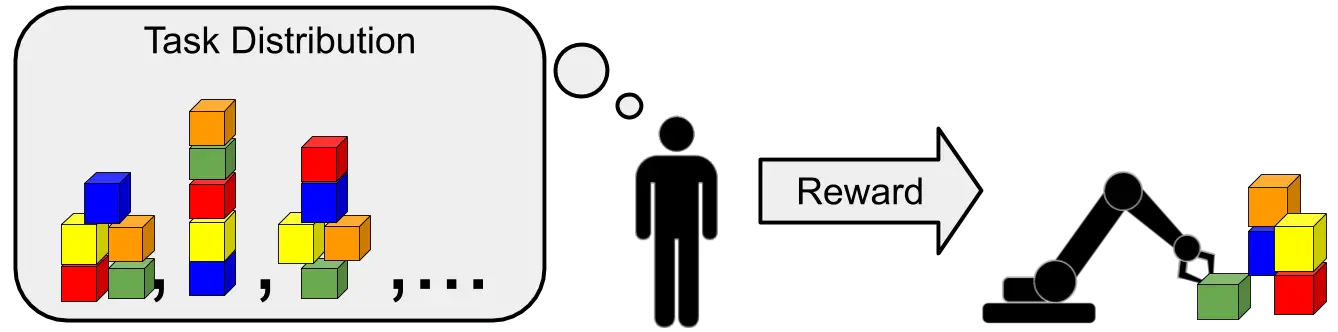
Una ilustración del meta-aprendizaje, donde las tareas corresponden a la disposición de los bloques
en diferentes tipos de torres. El humano tiene en mente una torre de bloques particular
y recompensa al robot cuando construye la torre correcta. El objetivo del robot es
construir la torre correcta tan pronto como sea posible.
En muchos escenarios queremos hacerlo bien en una distribución de tareas a la que tenemos
sólo un acceso limitado. Por ejemplo, en un coche que se conduce solo, las tareas pueden corresponder
para encontrar el equilibrio óptimo de suavidad, seguridad y eficiencia para cada
pero preguntar a los jinetes para obtener recompensas es caro. Un investigador puede
intentar construir manualmente una distribución de tareas que imite la verdadera tarea
distribución, pero esto puede ser muy difícil y llevar mucho tiempo. ¿Podemos
evitar tener que diseñar manualmente tales distribuciones de tareas?
Para responder a esta pregunta, debemos entender dónde los beneficios del meta-aprendizaje
…de donde vienen. Cuando definimos
distribuciones de tareas para el meta-aprendizaje, lo hacemos con algún conocimiento previo en
mente. Sin esta información previa, afinar las perillas de un procedimiento de aprendizaje
es a menudo un juego de suma cero: ajustar los mandos a cualquier configuración
acelerar el aprendizaje en algunas tareas mientras se ralentiza el aprendizaje en otras. ¿Desea
esto sugiere que no hay forma de ver el beneficio del meta-aprendizaje sin la
construcción manual de distribuciones de tareas? ¡Quizás no! La siguiente sección
presenta una alternativa.
Si el diseño de la distribución de tareas es el cuello de botella en la aplicación del meta-aprendizaje
¿por qué no hacer que los algoritmos de meta-aprendizaje propongan sus propias tareas? En
a primera vista esto parece una idea terrible, porque el teorema del almuerzo no gratis
sugiere que esto es imposible, sin conocimiento adicional. Sin embargo, muchos
Los escenarios del mundo real proporcionan un poco de información adicional, aunque
disfrazados como datos no etiquetados. Por ejemplo, en la regresión, podríamos tener
acceder a un conjunto de datos sin etiquetar y saber que las tareas posteriores serán
versiones etiquetadas de este mismo conjunto de datos de imágenes. En un entorno RL, un robot puede
interactuar con su entorno sin recibir ninguna recompensa, sabiendo que
las tareas posteriores se construirán definiendo funciones de recompensa para esta misma
el medio ambiente (es decir, el mundo real). Visto desde esta perspectiva, la receta para
meta-aprendizaje no supervisado (haciendo meta-aprendizaje sin construir manualmente
tareas) se vuelve claro: dado datos no etiquetados, construye distribuciones de tareas a partir de estos datos o entornos no etiquetados, y luego meta-aprende a resolver rápidamente estas tareas auto-propuestas.
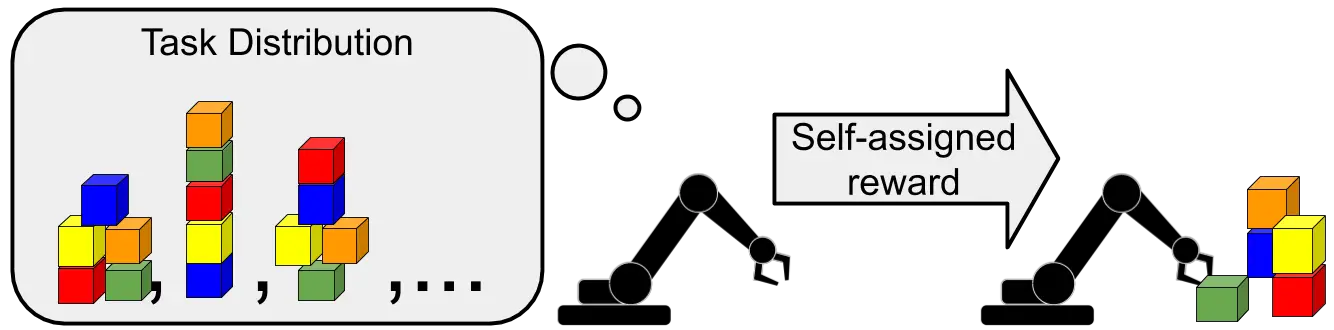
En el meta-aprendizaje no supervisado, el agente propone sus propias tareas, en lugar de
confiando en las tareas propuestas por un humano.
¿Cómo podemos usar estos datos sin etiquetar para construir distribuciones de tareas que
facilitar el aprendizaje de las tareas posteriores? En el caso de la regresión, el trabajo previo en
meta-aprendizaje no supervisado [Hsu 2018, Khodadadeh 2019]
agrupa un conjunto de datos de imágenes sin etiquetar y luego elige al azar subconjuntos de
los grupos para definir una distribución de las tareas de clasificación. Otros trabajos
[Jabri 2019] mira un escenario de RL: después de explorar un ambiente sin un
función de recompensa para recoger un conjunto de comportamientos que son factibles en este
estos comportamientos se agrupan y se utilizan para definir una distribución de
funciones de recompensa. En ambos casos, aunque las tareas construidas pueden ser
aleatorio, la distribución de tareas resultante no es aleatoria, porque todas las tareas comparten
los datos subyacentes no etiquetados – el conjunto de datos de imagen para la regresión y
la dinámica del entorno para el aprendizaje de refuerzo. El subyacente sin etiquetar
Los datos son el sesgo inductivo con el que pagamos nuestro almuerzo gratis.
Echemos un vistazo más profundo al caso de RL. Sin conocer las tareas posteriores o las funciones de recompensa, ¿cuál es la «mejor» distribución de tareas para «practicar» para resolver las tareas rápidamente? ¿Podemos medir cuán efectiva es la distribución de tareas para resolver lo desconocido,
tareas posteriores? ¿Hay algún sentido en el que una tarea no supervisada
mecanismo de propuesta es mejor que otro? Comprender las respuestas a estas
las preguntas pueden guiar el desarrollo de principios de los algoritmos de meta-aprendizaje con
poca dependencia de la supervisión humana. Nuestro trabajo [Gupta 2018]…toma un…
el primer paso para responder a estas preguntas. En particular, examinamos la
El peor de los casos de los procedimientos de aprendizaje, y derivar una óptima
procedimiento de aprendizaje no supervisado de meta-refuerzo.
Para responder a las preguntas planteadas anteriormente, nuestro primer paso es definir un óptimo
meta-aprendizaje para el caso en que se conozca la distribución de las tareas.
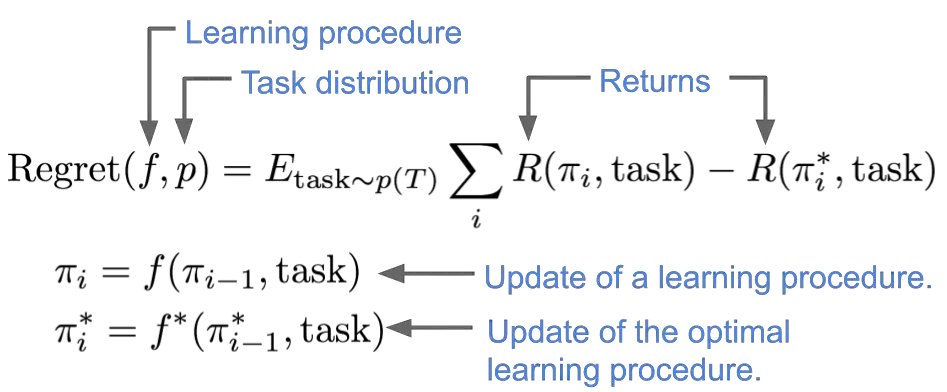
Definimos un óptimo meta-aprendizaje como el procedimiento de aprendizaje que logra el
la mayor recompensa esperada, promediada a través de la distribución de tareas. Más precisamente,
compararemos la recompensa esperada por un procedimiento de aprendizaje $f$
al de mejor procedimiento de aprendizaje $f^*$,
definiendo el lamenta de $f$ en una distribución de tareas $p$ como sigue:
Extendiendo esta definición al caso del meta-aprendizaje no supervisado, un óptimo
El meta-aprendiz sin supervisión puede definirse como un meta-aprendiz que logra el
mínimo El peor de los casos lamento en todas las posibles distribuciones de tareas que pueden ser
que se encuentran en el medio ambiente. En ausencia de cualquier conocimiento sobre la
tarea real de abajo, recurrimos a una formulación del peor caso. Una tarea no supervisada…
El algoritmo de meta-aprendizaje encontrará un único procedimiento de aprendizaje $f$ que tiene el
el más bajo arrepentimiento contra un adversariamente distribución de la tarea elegida $p$:
Nuestro trabajo analiza cómo exactamente podríamos obtener un óptimo sin supervisión
meta-aprendiz, y proporciona límites en el arrepentimiento que podría incurrir en el
El peor de los casos. Específicamente, bajo algunas restricciones en la familia de tareas que
podría encontrarse en el momento de la prueba, la distribución óptima para un
meta-aprendiz para proponer es uniforme sobre todas las tareas posibles.
La intuición para esto es sencilla: si la distribución de tareas del tiempo de prueba
puede ser elegido adversariamente, el algoritmo debe asegurarse de que es uniformemente bueno
sobre todos las posibles tareas que podrían encontrarse. Como ejemplo didáctico, si
las funciones de recompensa en tiempo de prueba se limitaban a la clase de tareas de alcance de objetivos,
el arrepentimiento por haber alcanzado un objetivo en tiempo de prueba es inverso al de la probabilidad
de tomar muestras de ese objetivo durante el tiempo de entrenamiento. Si alguno de los
los objetivos $g$ tienen menor densidad que los otros, un adversario puede proponer
una distribución de tareas que consiste únicamente en alcanzar ese objetivo $g$
causando que el procedimiento de aprendizaje incurra en un mayor arrepentimiento. Este ejemplo sugiere que podemos encontrar un óptimo meta-aprendiz sin supervisión usando una distribución uniforme sobre los objetivos. Nuestro trabajo formaliza esta idea y la extiende a clases más amplias de distribución de tareas.
Ahora, realmente el muestreo de una distribución uniforme en todas las tareas posibles es bastante desafiante.
Varios trabajos recientes han propuesto métodos de exploración de RL basados en maximizar
información mutua [Achiam 2018, Eysenbach 2018, Gregor 2016, Lee 2019, Sharma 2019].
En este trabajo, mostramos que estos métodos proporcionan una aproximación trazable a la distribución uniforme sobre las distribuciones de tareas. A
entender por qué esto es, podemos mirar la forma de una información mutua
considerado por [Eysenbach 2018]entre los estados $s$ y latente
variables $z$:
En este objetivo, el primer término de entropía marginal se maximiza cuando hay una
distribución uniforme en todas las tareas posibles. La segunda entropía condicional
asegura la consistencia, asegurándose de que por cada $z$, el resultado
la distribución de $s$ es estrecha. Esto sugiere construir sin supervisión
distribución de tareas en un entorno optimizando la información mutua
nos da una distribución de tareas probadamente óptima, de acuerdo con nuestra
la noción de la optimización min-max.
Aunque el análisis hace algunas suposiciones limitantes sobre las formas de las tareas
encontramos, mostramos cómo este análisis puede extenderse para proporcionar un límite de
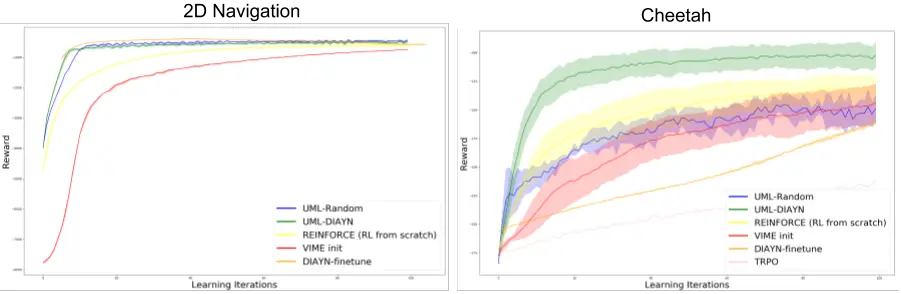
el rendimiento en el caso más general de aprendizaje de refuerzo. También
proporciona ganancias empíricas en varios entornos simulados en comparación con
métodos que se entrenan desde cero, como se muestra en la siguiente figura.
En resumen:
- Los procedimientos de aprendizaje son recetas para convertir conjuntos de datos en función
aproximadores. Los procedimientos de aprendizaje tienen muchas perillas, que pueden ser afinadas por
optimizando los procedimientos de aprendizaje para resolver una distribución de tareas. - El diseño manual de estas distribuciones de tareas es un desafío, por lo que una línea reciente
de trabajo sugiere que el procedimiento de aprendizaje puede utilizar datos no etiquetados para
propone sus propias tareas para optimizar sus perillas. - Estos algoritmos de meta-aprendizaje no supervisados permiten el aprendizaje en regímenes
anteriormente poco práctico, y ampliar aún más esa capacidad de la máquina
métodos de aprendizaje. - Este trabajo se relaciona estrechamente con otros trabajos sobre la habilidad no supervisada
el descubrimiento, la exploración y el aprendizaje de la representación, pero
optimiza explícitamente la transferibilidad de las representaciones y habilidades para
tareas posteriores.
Quedan varias preguntas abiertas sobre el meta-aprendizaje no supervisado:
- El aprendizaje no supervisado está estrechamente relacionado con el meta-aprendizaje no supervisado: el
el primero utiliza datos sin etiquetar para aprender características, mientras que el segundo utiliza datos sin etiquetar
datos para afinar el procedimiento de aprendizaje. ¿Podría haber algún tratamiento unificador
de ambos enfoques? - Nuestro análisis sólo prueba que la propuesta de tareas basada en la información mutua es óptima para los algoritmos de meta-aprendizaje sin memoria. Los algoritmos de meta-aprendizaje con memoria, que esperamos que funcionen mejor, pueden funcionar mejor con diferentes mecanismos de propuesta de tareas.
- Escalar el meta aprendizaje no supervisado para aprovechar los conjuntos de datos a gran escala y
tareas complejas encierra la promesa de adquirir procedimientos de aprendizaje para resolver
problemas del mundo real más eficientemente que nuestros actuales procedimientos de aprendizaje.
Revise nuestro documento para más experimentos y pruebas: https://arxiv.org/abs/1806.04640
Agradecimientos
Gracias a Jake Tyo, Conor Igoe, Sergey Levine, Chelsea Finn, Misha Khodak, Daniel Seita y Stefani Karp por sus comentarios.
