XGBoost es una implementación poderosa y efectiva del algoritmo de conjunto de aumento de gradiente.
Puede ser un desafío configurar los hiperparámetros de los modelos XGBoost, lo que a menudo conduce al uso de experimentos de búsqueda de cuadrícula grandes que consumen mucho tiempo y son computacionalmente costosos.
Un enfoque alternativo para configurar XGBoost modelos es evaluar el rendimiento del modelo en cada iteración del algoritmo durante el entrenamiento y trazar los resultados como curvas de aprendizaje. Estos gráficos de la curva de aprendizaje proporcionan una herramienta de diagnóstico que se puede interpretar y sugieren cambios específicos en los hiperparámetros del modelo que pueden conducir a mejoras en el rendimiento predictivo.
En este tutorial, descubrirá cómo trazar e interpretar curvas de aprendizaje para modelos XGBoost en Python.
Después de completar este tutorial, sabrá:
- Las curvas de aprendizaje proporcionan una herramienta de diagnóstico útil para comprender la dinámica de entrenamiento de modelos de aprendizaje supervisado como XGBoost.
- Cómo configurar XGBoost para evaluar conjuntos de datos en cada iteración y trazar los resultados como curvas de aprendizaje.
- Cómo interpretar y utilizar gráficos de curvas de aprendizaje para mejorar el rendimiento del modelo XGBoost.
Empecemos.

Ajuste el rendimiento de XGBoost con curvas de aprendizaje
Foto de Bernard Spragg. NZ, algunos derechos reservados.
Descripción general del tutorial
Este tutorial se divide en cuatro partes; Ellos son:
- Aumento de gradiente extremo
- Curvas de aprendizaje
- Trazar la curva de aprendizaje de XGBoost
- Ajuste el modelo de XGBoost mediante curvas de aprendizaje
Aumento de gradiente extremo
Aumento de gradiente se refiere a una clase de algoritmos conjuntos de aprendizaje automático que se pueden utilizar para problemas de modelado predictivo de clasificación o regresión.
Los conjuntos se construyen a partir de modelos de árboles de decisión. Los árboles se agregan uno a la vez al conjunto y se ajustan para corregir los errores de predicción realizados por modelos anteriores. Este es un tipo de modelo de aprendizaje automático de conjunto denominado impulso.
Los modelos se ajustan utilizando cualquier función de pérdida diferenciable arbitraria y algoritmo de optimización de descenso de gradiente. Esto le da a la técnica su nombre, «aumento de gradiente», ya que el gradiente de pérdida se minimiza a medida que el modelo se ajusta, al igual que una red neuronal.
Para obtener más información sobre el aumento de gradiente, consulte el tutorial:
Extreme Gradient Boosting, o XGBoost para abreviar, es una implementación eficiente de código abierto del algoritmo de aumento de gradiente. Como tal, XGBoost es un algoritmo, un proyecto de código abierto y una biblioteca de Python.
Inicialmente fue desarrollado por Tianqi Chen y fue descrito por Chen y Carlos Guestrin en su artículo de 2016 titulado «XGBoost: A Scalable Tree Boosting System».
Está diseñado para ser computacionalmente eficiente (por ejemplo, rápido de ejecutar) y altamente efectivo, quizás más efectivo que otras implementaciones de código abierto.
Las dos razones principales para utilizar XGBoost son la velocidad de ejecución y el rendimiento del modelo.
XGBoost domina los conjuntos de datos estructurados o tabulares sobre problemas de modelado predictivo de clasificación y regresión. La evidencia es que es el algoritmo de referencia para los ganadores de la competencia en la plataforma de ciencia de datos competitiva de Kaggle.
Entre las 29 soluciones ganadoras de desafíos 3 publicadas en el blog de Kaggle durante 2015, 17 soluciones utilizaron XGBoost. […] El éxito del sistema también se vio en KDDCup 2015, donde XGBoost fue utilizado por todos los equipos ganadores en el top 10.
– XGBoost: un sistema de aumento de árboles escalable, 2016.
Para obtener más información sobre XGBoost y cómo instalar y usar la API de XGBoost Python, consulte el tutorial:
Ahora que estamos familiarizados con lo que es XGBoost y por qué es importante, echemos un vistazo más de cerca a las curvas de aprendizaje.
Curvas de aprendizaje
Generalmente, una curva de aprendizaje es una gráfica que muestra el tiempo o la experiencia en el eje xy el aprendizaje o la mejora en el eje y.
Las curvas de aprendizaje se utilizan ampliamente en el aprendizaje automático para algoritmos que aprenden (optimizan sus parámetros internos) de forma incremental a lo largo del tiempo, como las redes neuronales de aprendizaje profundo.
La métrica utilizada para evaluar el aprendizaje podría maximizarse, lo que significa que mejores puntuaciones (números más grandes) indican más aprendizaje. Un ejemplo sería la precisión de la clasificación.
Es más común usar una puntuación que se minimiza, como la pérdida o el error, en la que mejores puntuaciones (números más pequeños) indican más aprendizaje y un valor de 0.0 indica que el conjunto de datos de entrenamiento se aprendió perfectamente y no se cometieron errores.
Durante el entrenamiento de un modelo de aprendizaje automático, se puede evaluar el estado actual del modelo en cada paso del algoritmo de entrenamiento. Se puede evaluar en el conjunto de datos de entrenamiento para dar una idea de qué tan bien es el modelo «aprendiendo. » También se puede evaluar en un conjunto de datos de validación de reserva que no forma parte del conjunto de datos de entrenamiento. La evaluación del conjunto de datos de validación da una idea de qué tan bien está el modelo «generalizando. «
Es común crear curvas de aprendizaje dual para un modelo de aprendizaje automático durante el entrenamiento en los conjuntos de datos de entrenamiento y validación.
La forma y la dinámica de una curva de aprendizaje se pueden utilizar para diagnosticar el comportamiento de un modelo de aprendizaje automático y, a su vez, quizás sugerir el tipo de cambios de configuración que se pueden realizar para mejorar el aprendizaje y / o el rendimiento.
Hay tres dinámicas comunes que probablemente observará en las curvas de aprendizaje; Ellos son:
- Underfit.
- Overfit.
- Buen ajuste.
Por lo general, las curvas de aprendizaje se utilizan para diagnosticar el comportamiento de sobreajuste de un modelo que se puede abordar ajustando los hiperparámetros del modelo.
El sobreajuste se refiere a un modelo que ha aprendido demasiado bien el conjunto de datos de entrenamiento, incluido el ruido estadístico o las fluctuaciones aleatorias en el conjunto de datos de entrenamiento.
El problema con el sobreajuste es que cuanto más especializado se vuelve el modelo para los datos de entrenamiento, menor es la capacidad de generalizar a nuevos datos, lo que resulta en un aumento en el error de generalización. Este aumento en el error de generalización se puede medir por el rendimiento del modelo en el conjunto de datos de validación.
Para obtener más información sobre las curvas de aprendizaje, consulte el tutorial:
Ahora que estamos familiarizados con las curvas de aprendizaje, veamos cómo podemos trazar las curvas de aprendizaje para los modelos XGBoost.
Trazar la curva de aprendizaje de XGBoost
En esta sección, trazaremos la curva de aprendizaje para un modelo XGBoost.
Primero, necesitamos un conjunto de datos para usar como base para ajustar y evaluar el modelo.
Usaremos un conjunto de datos de clasificación sintético binario (dos clases) en este tutorial.
La función make_classification () scikit-learn se puede utilizar para crear un conjunto de datos de clasificación sintético. En este caso, usaremos 50 características de entrada (columnas) y generaremos 10,000 muestras (filas). La semilla para el generador de números pseudoaleatorios es fija para asegurar la misma base «problema”Se utiliza cada vez que se generan muestras.
El siguiente ejemplo genera el conjunto de datos de clasificación sintético y resume la forma de los datos generados.
|
# conjunto de datos de clasificación de prueba desde sklearn.conjuntos de datos importar hacer_clasificación # definir conjunto de datos X, y = make_classification(n_samples=10000, n_features=50, n_informativo=50, n_redundante=0, estado_aleatorio=1) # resumir el conjunto de datos imprimir(X.forma, y.forma) |
La ejecución del ejemplo genera los datos y reporta el tamaño de los componentes de entrada y salida, confirmando la forma esperada.
A continuación, podemos ajustar un modelo XGBoost en este conjunto de datos y trazar curvas de aprendizaje.
Primero, debemos dividir el conjunto de datos en una porción que se usará para entrenar el modelo (entrenar) y otra porción que no se usará para entrenar el modelo, pero se retendrá y se usará para evaluar el modelo en cada paso del entrenamiento. algoritmo (conjunto de prueba o conjunto de validación).
|
... # dividir los datos en trenes y conjuntos de prueba X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0,50, estado_aleatorio=1) |
Luego podemos definir un modelo de clasificación XGBoost con hiperparámetros predeterminados.
|
... # definir el modelo modelo = Clasificador XGB() |
A continuación, el modelo se puede ajustar al conjunto de datos.
En este caso, debemos especificar al algoritmo de entrenamiento que queremos que evalúe el rendimiento del modelo en el tren y los conjuntos de pruebas en cada iteración (por ejemplo, después de que se agregue cada nuevo árbol al conjunto).
Para hacer esto debemos especificar los conjuntos de datos a evaluar y la métrica a evaluar.
El conjunto de datos debe especificarse como una lista de tuplas, donde cada tupla contiene las columnas de entrada y salida de un conjunto de datos y cada elemento de la lista es un conjunto de datos diferente para evaluar, p. Ej. el tren y los equipos de prueba.
|
... # definir los conjuntos de datos para evaluar cada iteración evalset = [[(X_train, y_train), (X_test,y_test)] |
Hay muchas métricas que podemos querer evaluar, aunque dado que es una tarea de clasificación, evaluaremos la pérdida logarítmica (entropía cruzada) del modelo, que es una puntuación minimizadora (los valores más bajos son mejores).
Esto se puede lograr especificando el «eval_metric«Argumento al llamar encajar() y proporcionándole el nombre de la métrica que evaluaremos «logloss«. También podemos especificar los conjuntos de datos para evaluar mediante el «eval_set» argumento. El encajar() La función toma el conjunto de datos de entrenamiento como los dos primeros argumentos de forma normal.
|
... # encajar en el modelo modelo.encajar(X_train, y_train, eval_metric=‘logloss’, eval_set=evalset) |
Una vez que el modelo se ajusta, podemos evaluar su desempeño como la precisión de clasificación en el conjunto de datos de prueba.
|
... # evaluar el desempeño yhat = modelo.predecir(X_test) puntaje = puntuación_de_precisión(y_test, yhat) imprimir(‘Precisión:% .3f’ % puntaje) |
Luego podemos recuperar las métricas calculadas para cada conjunto de datos a través de una llamada al evals_result () función.
|
... # recuperar métricas de rendimiento resultados = modelo.evals_result() |
Esto devuelve un diccionario organizado primero por conjunto de datos («validation_0‘ y ‘validation_1‘) Y luego por métrica (‘logloss‘).
Podemos crear gráficos de líneas de métricas para cada conjunto de datos.
|
... # trazar curvas de aprendizaje pyplot.trama(resultados[[‘validación_0’][[‘logloss’], etiqueta=‘entrenar’) pyplot.trama(resultados[[‘validation_1’][[‘logloss’], etiqueta=‘prueba’) # muestra la leyenda pyplot.leyenda() # mostrar la trama pyplot.show() |
Y eso es.
Al unir todo esto, el ejemplo completo de cómo ajustar un modelo XGBoost en la tarea de clasificación sintética y trazar curvas de aprendizaje se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 |
# trazar la curva de aprendizaje de un modelo xgboost desde sklearn.conjuntos de datos importar make_classification desde sklearn.model_selection importar train_test_split desde sklearn.métrica importar puntuación_de_precisión desde xgboost importar Clasificador XGB desde matplotlib importar pyplot # definir conjunto de datos X, y = make_classification(n_samples=10000, n_features=50, n_informativo=50, n_redundante=0, estado_aleatorio=1) # dividir los datos en trenes y conjuntos de prueba X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0,50, estado_aleatorio=1) # definir el modelo modelo = Clasificador XGB() # definir los conjuntos de datos para evaluar cada iteración evalset = [[(X_train, y_train), (X_test,y_test)] # encajar en el modelo modelo.encajar(X_train, y_train, eval_metric=‘logloss’, eval_set=evalset) # evaluar el desempeño yhat = modelo.predecir(X_test) puntaje = precisión_puntaje(y_test, yhat) imprimir(‘Precisión:% .3f’ % puntaje) # recuperar métricas de rendimiento resultados = modelo.evals_result() # trazar curvas de aprendizaje pyplot.trama(resultados[[‘validación_0’][[‘logloss’], etiqueta=‘entrenar’) pyplot.trama(resultados[[‘validation_1’][[‘logloss’], etiqueta=‘prueba’) # muestra la leyenda pyplot.leyenda() # mostrar la trama pyplot.show() |
La ejecución del ejemplo se ajusta al modelo XGBoost, recupera las métricas calculadas y traza curvas de aprendizaje.
Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o procedimiento de evaluación, o las diferencias en la precisión numérica. Considere ejecutar el ejemplo varias veces y compare el resultado promedio.
En primer lugar, se informa el rendimiento del modelo, lo que muestra que el modelo logró una precisión de clasificación de aproximadamente el 94,5% en el conjunto de pruebas de retención.
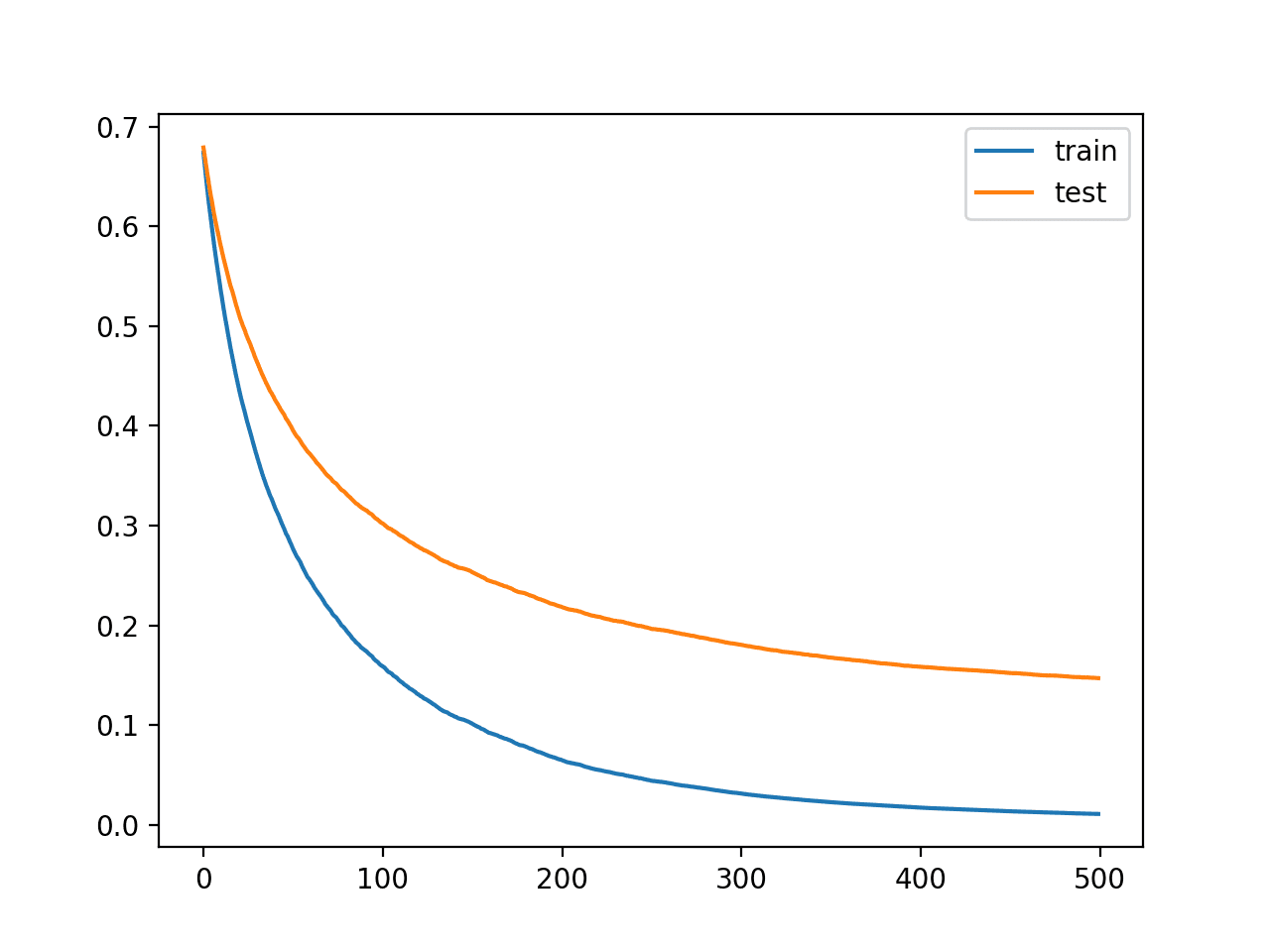
La gráfica muestra curvas de aprendizaje para el conjunto de datos de prueba y tren donde el eje x es el número de iteraciones del algoritmo (o el número de árboles agregados al conjunto) y el eje y es la pérdida logarítmica del modelo. Cada línea muestra la pérdida logarítmica por iteración para un conjunto de datos determinado.
A partir de las curvas de aprendizaje, podemos ver que el rendimiento del modelo en el conjunto de datos de entrenamiento (línea azul) es mejor o tiene una pérdida menor que el rendimiento del modelo en el conjunto de datos de prueba (línea naranja), como podríamos esperar generalmente.
Curvas de aprendizaje para el modelo XGBoost en el conjunto de datos de clasificación sintético
Ahora que sabemos cómo trazar curvas de aprendizaje para modelos XGBoost, veamos cómo podemos usar las curvas para mejorar el rendimiento del modelo.
Ajuste el modelo de XGBoost mediante curvas de aprendizaje
Podemos utilizar las curvas de aprendizaje como herramienta de diagnóstico.
Las curvas se pueden interpretar y utilizar como base para sugerir cambios específicos en la configuración del modelo que podrían resultar en un mejor rendimiento.
El modelo y el resultado de la sección anterior se pueden utilizar como línea de base y punto de partida.
Al observar el gráfico, podemos ver que ambas curvas están inclinadas hacia abajo y sugieren que más iteraciones (agregar más árboles) pueden resultar en una mayor disminución de la pérdida.
Probémoslo.
Podemos aumentar el número de iteraciones del algoritmo a través del «n_estimators«Hiperparámetro que tiene un valor predeterminado de 100. Incremémoslo a 500.
|
... # definir el modelo modelo = Clasificador XGB(n_estimators=500) |
El ejemplo completo se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 |
# trazar la curva de aprendizaje de un modelo xgboost desde sklearn.conjuntos de datos importar make_classification desde sklearn.model_selection importar train_test_split desde sklearn.métrica importar precisión_puntaje desde xgboost importar Clasificador XGB desde matplotlib importar pyplot # definir conjunto de datos X, y = make_classification(n_samples=10000, n_features=50, n_informativo=50, n_redundante=0, estado_aleatorio=1) # dividir los datos en trenes y conjuntos de prueba X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0,50, estado_aleatorio=1) # definir el modelo modelo = Clasificador XGB(n_estimators=500) # definir los conjuntos de datos para evaluar cada iteración evalset = [[(X_train, y_train), (X_test,y_test)] # encajar en el modelo modelo.encajar(X_train, y_train, eval_metric=‘logloss’, eval_set=evalset) # evaluar el desempeño yhat = modelo.predecir(X_test) puntaje = puntuación_de_precisión(y_test, yhat) imprimir(‘Precisión:% .3f’ % puntaje) # recuperar métricas de rendimiento resultados = modelo.evals_result() # trazar curvas de aprendizaje pyplot.trama(resultados[[‘validación_0’][[‘logloss’], etiqueta=‘entrenar’) pyplot.trama(resultados[[‘validation_1’][[‘logloss’], etiqueta=‘prueba’) # muestra la leyenda pyplot.leyenda() # mostrar la trama pyplot.show() |
La ejecución del ejemplo ajusta y evalúa el modelo y traza las curvas de aprendizaje del rendimiento del modelo.
Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o procedimiento de evaluación, o las diferencias en la precisión numérica. Considere ejecutar el ejemplo varias veces y compare el resultado promedio.
Podemos ver que más iteraciones han dado como resultado un aumento en la precisión de aproximadamente un 94,5% a aproximadamente un 95,8%.
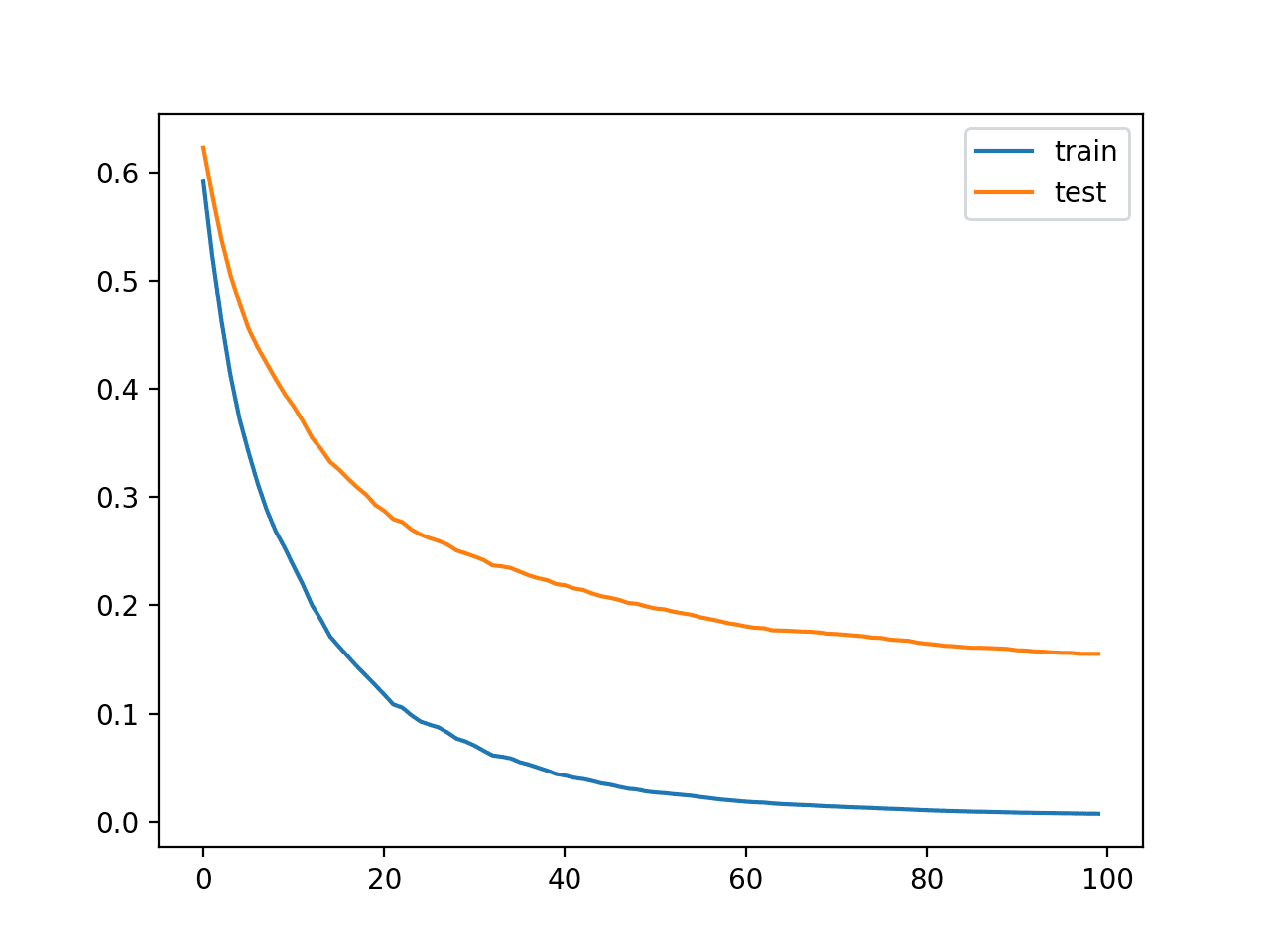
Podemos ver en las curvas de aprendizaje que, de hecho, las iteraciones adicionales del algoritmo hicieron que las curvas continuaran cayendo y luego se nivelaran después de quizás 150 iteraciones, donde permanecen razonablemente planas.
Curvas de aprendizaje para el modelo XGBoost con más iteraciones
Las curvas largas y planas pueden sugerir que el algoritmo está aprendiendo demasiado rápido y podemos beneficiarnos de hacerlo más lento.
Esto se puede lograr utilizando la tasa de aprendizaje, que limita la contribución de cada árbol agregado al conjunto. Esto se puede controlar mediante el «eta”Hiperparámetro y el valor predeterminado es 0,3. Podemos probar con un valor menor, como 0.05.
|
... # definir el modelo modelo = Clasificador XGB(n_estimators=500, eta=0,05) |
El ejemplo completo se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 |
# trazar la curva de aprendizaje de un modelo xgboost desde sklearn.conjuntos de datos importar make_classification desde sklearn.model_selection importar train_test_split desde sklearn.métrica importar puntuación_de_precisión desde xgboost importar Clasificador XGB desde matplotlib importar pyplot # definir conjunto de datos X, y = make_classification(n_samples=10000, n_features=50, n_informativo=50, n_redundante=0, estado_aleatorio=1) # dividir los datos en trenes y conjuntos de prueba X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0,50, estado_aleatorio=1) # definir el modelo modelo = Clasificador XGB(n_estimators=500, eta=0,05) # definir los conjuntos de datos para evaluar cada iteración evalset = [[(X_train, y_train), (X_test,y_test)] # encajar en el modelo modelo.encajar(X_train, y_train, eval_metric=‘logloss’, eval_set=evalset) # evaluar el desempeño yhat = modelo.predecir(X_test) puntaje = puntuación_de_precisión(y_test, yhat) imprimir(‘Precisión:% .3f’ % puntaje) # recuperar métricas de rendimiento resultados = modelo.evals_result() # trazar curvas de aprendizaje pyplot.trama(resultados[[‘validación_0’][[‘logloss’], etiqueta=‘entrenar’) pyplot.trama(resultados[[‘validation_1’][[‘logloss’], etiqueta=‘prueba’) # muestra la leyenda pyplot.leyenda() # mostrar la trama pyplot.show() |
La ejecución del ejemplo ajusta y evalúa el modelo y traza las curvas de aprendizaje del rendimiento del modelo.
Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o procedimiento de evaluación, o las diferencias en la precisión numérica. Considere ejecutar el ejemplo varias veces y compare el resultado promedio.
Podemos ver que la menor tasa de aprendizaje ha empeorado la precisión, pasando de aproximadamente un 95,8% a aproximadamente un 95,1%.
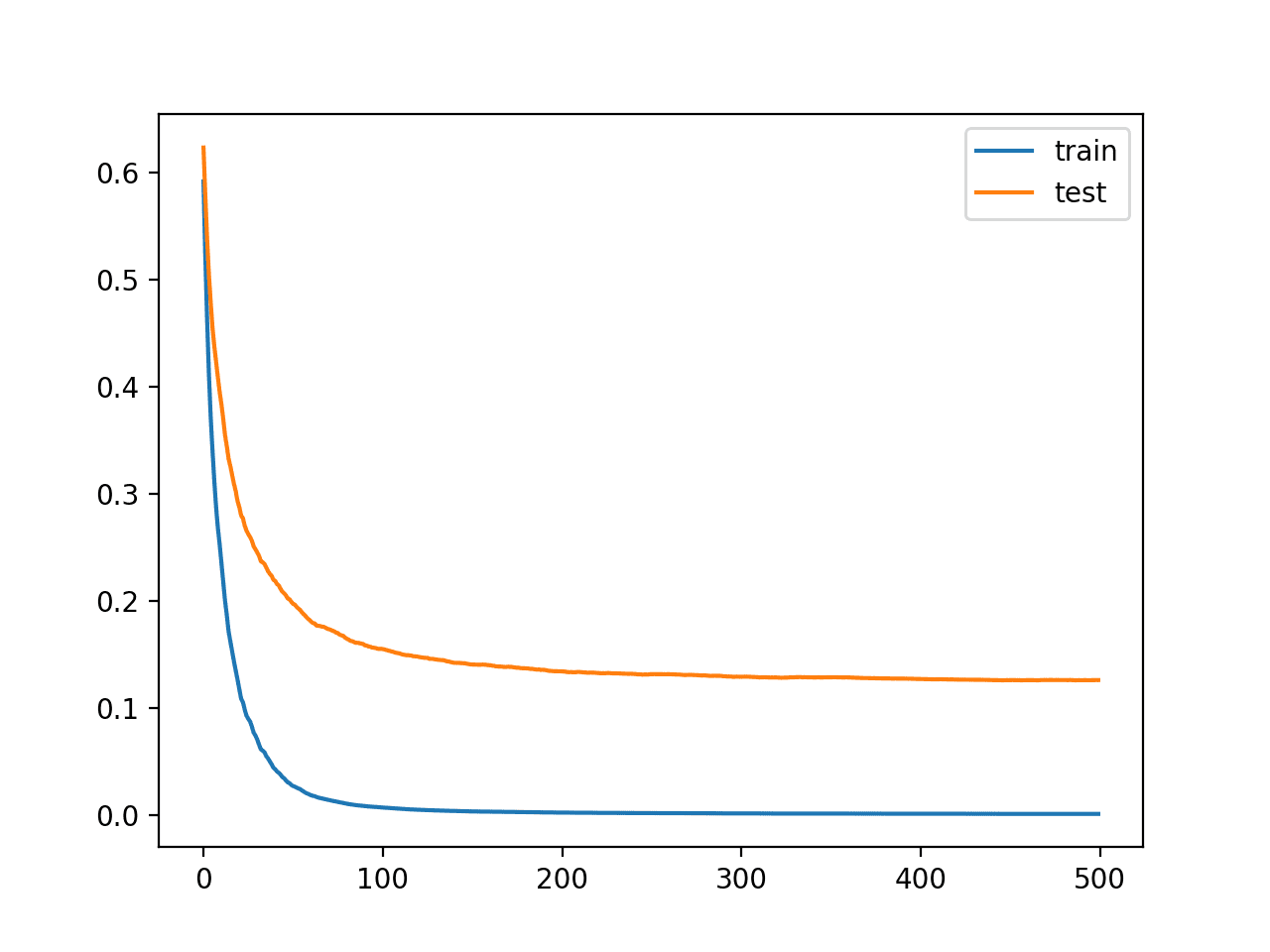
Podemos ver en las curvas de aprendizaje que, de hecho, el aprendizaje se ha ralentizado. Las curvas sugieren que podemos continuar agregando más iteraciones y quizás lograr un mejor desempeño ya que las curvas tendrían más oportunidades de continuar disminuyendo.

Curvas de aprendizaje para el modelo XGBoost con menor tasa de aprendizaje
Intentemos aumentar el número de iteraciones de 500 a 2000.
|
... # definir el modelo modelo = Clasificador XGB(n_estimators=2000, eta=0,05) |
El ejemplo completo se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 |
# plot learning curve of an xgboost model desde sklearn.datasets import make_classification desde sklearn.model_selection import train_test_split desde sklearn.metrics import accuracy_score desde xgboost import XGBClassifier desde matplotlib import pyplot # define dataset X, y = make_classification(n_samples=10000, n_features=50, n_informative=50, n_redundant=0, random_state=1) # split data into train and test sets X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.50, random_state=1) # define the model model = XGBClassifier(n_estimators=2000, eta=0.05) # define the datasets to evaluate each iteration evalset = [[(X_train, y_train), (X_test,y_test)] # fit the model model.fit(X_train, y_train, eval_metric=‘logloss’, eval_set=evalset) # evaluate performance yhat = model.predict(X_test) score = accuracy_score(y_test, yhat) print(‘Accuracy: %.3f’ % score) # retrieve performance metrics results = model.evals_result() # plot learning curves pyplot.plot(results[[‘validation_0’][[‘logloss’], label=‘train’) pyplot.plot(results[[‘validation_1’][[‘logloss’], label=‘test’) # show the legend pyplot.legend() # show the plot pyplot.show() |
Running the example fits and evaluates the model and plots the learning curves of model performance.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
We can see that more iterations have given the algorithm more space to improve, achieving an accuracy of 96.1%, the best so far.
The learning curves again show a stable convergence of the algorithm with a steep decrease and long flattening out.
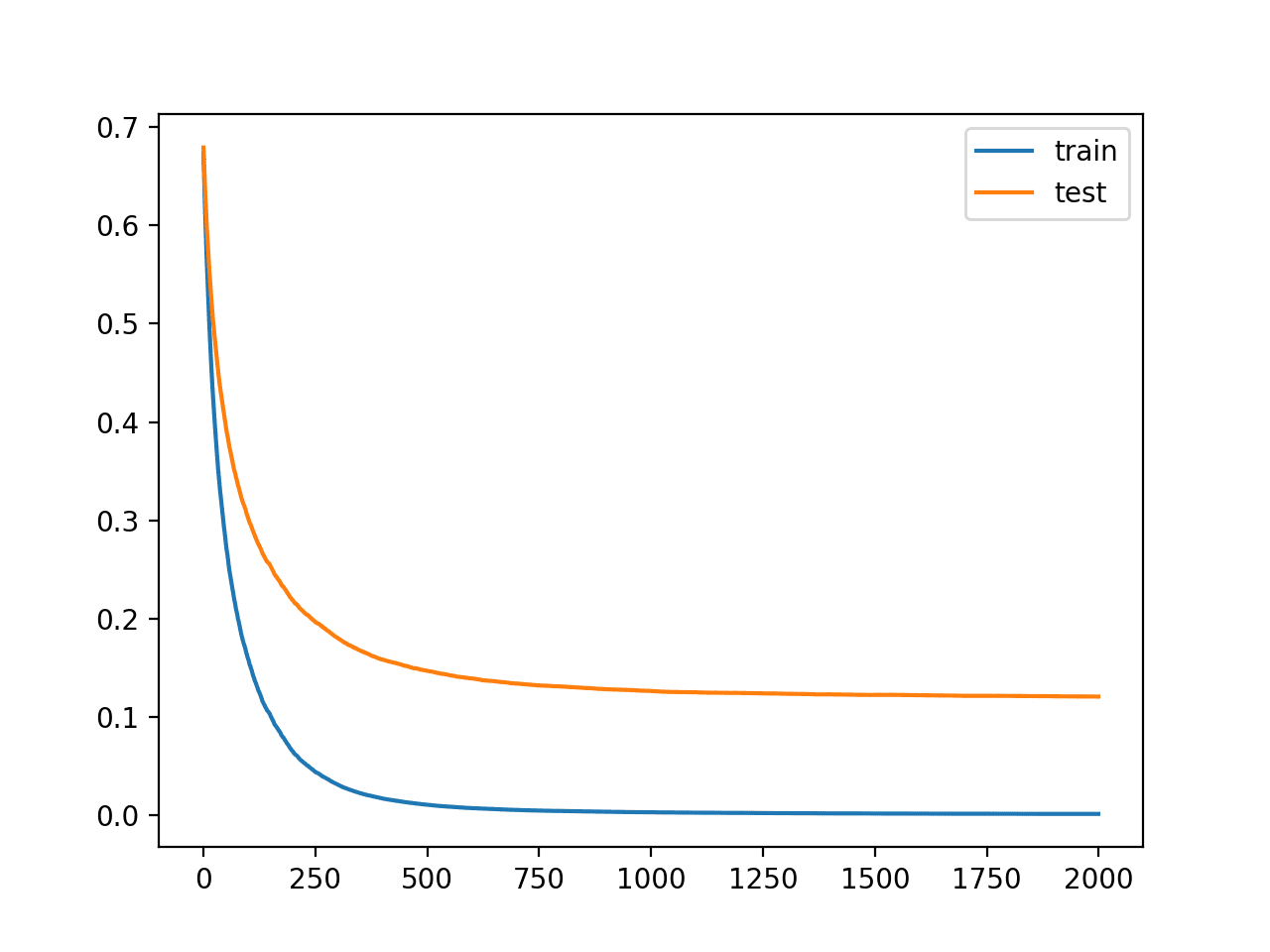
Learning Curves for the XGBoost Model With Smaller Learning Rate and Many Iterations
We could repeat the process of decreasing the learning rate and increasing the number of iterations to see if further improvements are possible.
Another approach to slowing down learning is to add regularization in the form of reducing the number of samples and features (rows and columns) used to construct each tree in the ensemble.
In this case, we will try halving the number of samples and features respectively via the “subsample” and “colsample_bytree” hyperparameters.
|
... # define the model model = XGBClassifier(n_estimators=2000, eta=0.05, subsample=0.5, colsample_bytree=0.5) |
The complete example is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 |
# plot learning curve of an xgboost model desde sklearn.datasets import make_classification desde sklearn.model_selection import train_test_split desde sklearn.metrics import accuracy_score desde xgboost import XGBClassifier desde matplotlib import pyplot # define dataset X, y = make_classification(n_samples=10000, n_features=50, n_informative=50, n_redundant=0, random_state=1) # split data into train and test sets X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.50, random_state=1) # define the model model = XGBClassifier(n_estimators=2000, eta=0.05, subsample=0.5, colsample_bytree=0.5) # define the datasets to evaluate each iteration evalset = [[(X_train, y_train), (X_test,y_test)] # fit the model model.fit(X_train, y_train, eval_metric=‘logloss’, eval_set=evalset) # evaluate performance yhat = model.predict(X_test) score = accuracy_score(y_test, yhat) print(‘Accuracy: %.3f’ % score) # retrieve performance metrics results = model.evals_result() # plot learning curves pyplot.plot(results[[‘validation_0’][[‘logloss’], label=‘train’) pyplot.plot(results[[‘validation_1’][[‘logloss’], label=‘test’) # show the legend pyplot.legend() # show the plot pyplot.show() |
Running the example fits and evaluates the model and plots the learning curves of model performance.
Note: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
We can see that the addition of regularization has resulted in a further improvement, bumping accuracy from about 96.1% to about 96.6%.
The curves suggest that regularization has slowed learning and that perhaps increasing the number of iterations may result in further improvements.
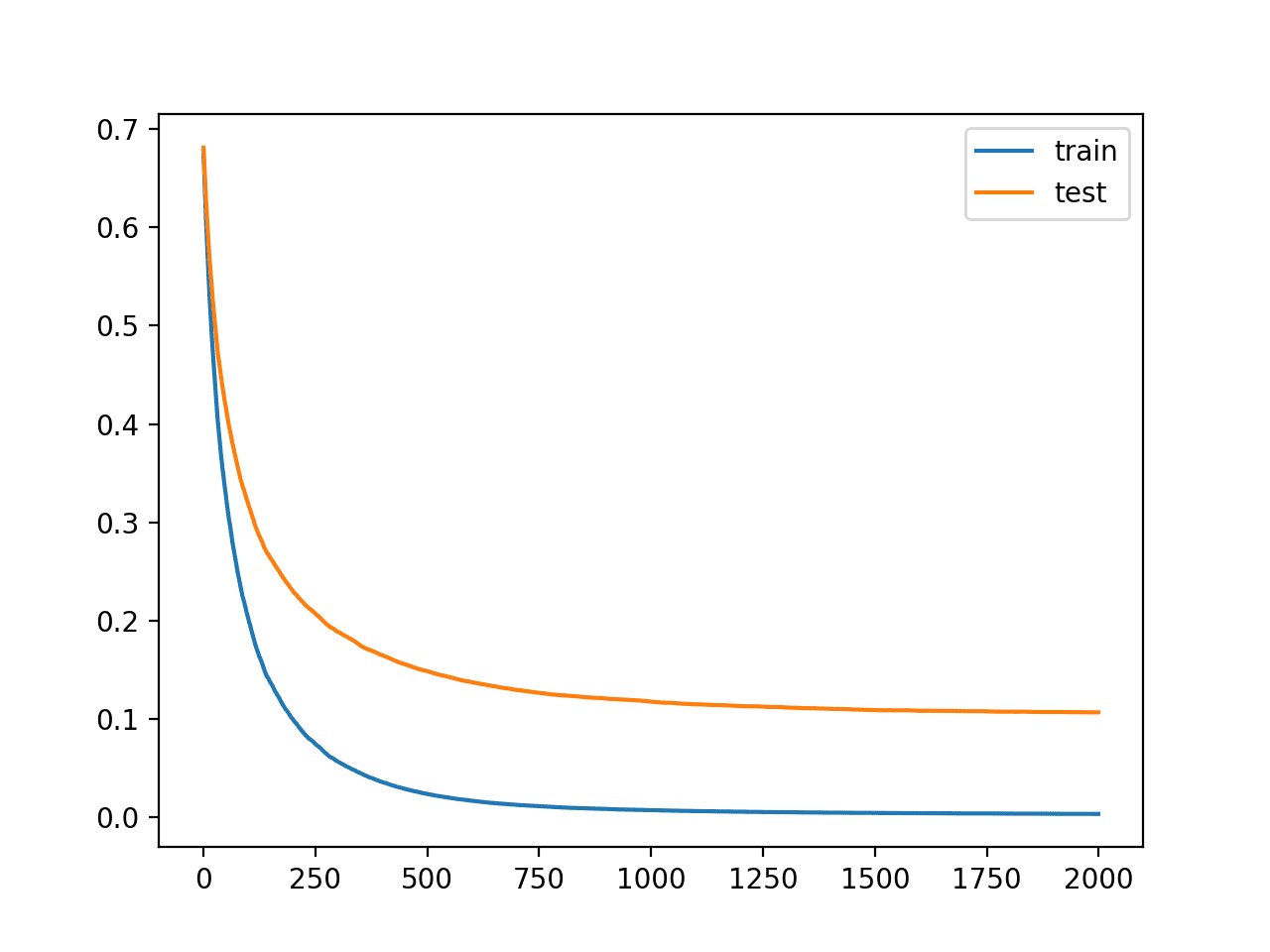
Learning Curves for the XGBoost Model with Regularization
This process can continue, and I am interested to see what you can come up with.
Further Reading
This section provides more resources on the topic if you are looking to go deeper.
Tutorials
Papers
APIs
Summary
In this tutorial, you discovered how to plot and interpret learning curves for XGBoost models in Python.
Specifically, you learned:
- Learning curves provide a useful diagnostic tool for understanding the training dynamics of supervised learning models like XGBoost.
- How to configure XGBoost to evaluate datasets each iteration and plot the results as learning curves.
- How to interpret and use learning curve plots to improve XGBoost model performance.
Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.

