Imagine que está construyendo la próxima generación de modelos de aprendizaje automático para la transcripción de la escritura. Basándose en iteraciones anteriores de su producto, ha identificado un desafío clave para este despliegue: después de la implementación, los nuevos usuarios finales suelen tener estilos de escritura diferentes y no vistos, lo que lleva a cambio de distribución. Una solución para este desafío es aprender un adaptable modelo que puede especializarse y ajustarse al estilo de escritura de cada usuario con el tiempo. Esta solución parece prometedora, pero debe equilibrarse con las preocupaciones sobre la facilidad de uso: exigir a los usuarios que proporcionen información sobre el modelo puede ser engorroso y obstaculizar su adopción. ¿Es posible, en cambio, aprender un modelo que pueda adaptarse a los nuevos usuarios sin etiquetas?
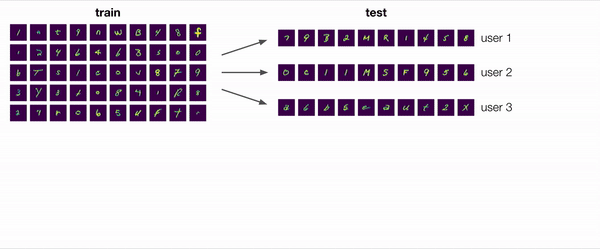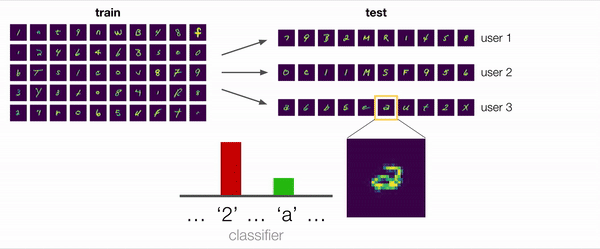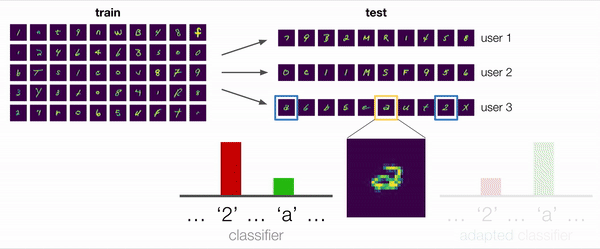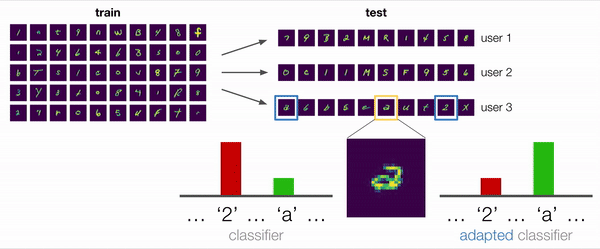
En muchos escenarios, incluyendo este ejemplo, la respuesta es «sí». Consideremos el ambiguo ejemplo que se muestra ampliado en la figura siguiente. ¿Este personaje es un «2» con un lazo o una «a» de doble piso? Para un modelo no adaptativo que preste atención a los sesgos de los datos de entrenamiento, la predicción razonable sería «2». Sin embargo, incluso sin etiquetas, podemos extraer información útil de los demás ejemplos del usuario: un modelo adaptativo, por ejemplo, puede observar que este usuario ha escrito «2» sin bucles y concluir que este personaje es, por lo tanto, más probable que sea «a».
Manejar el cambio de distribución que surge del despliegue de un modelo a nuevos usuarios es un ejemplo importante de motivación para la adaptación no etiquetada. Pero, este no es ni mucho menos el único ejemplo. En un mundo en constante cambio, los automóviles autónomos deben adaptarse a nuevas condiciones climáticas y ubicaciones, los clasificadores de imagen deben adaptarse a nuevas cámaras con diferentes intrínsecos y los sistemas de recomendación deben adaptarse a las cambiantes preferencias de los usuarios. Los seres humanos han demostrado la capacidad de adaptarse sin etiquetas al deducir la información de la distribución de los ejemplos de prueba. ¿Podemos desarrollar métodos que permitan a los modelos de aprendizaje automático hacer lo mismo?
Esta cuestión ha sido objeto de una atención creciente por parte de los investigadores, y en varios trabajos recientes se han propuesto métodos para la adaptación del tiempo de prueba sin etiquetar. En este artículo, estudiaré estos trabajos así como otros marcos destacados para manejar el cambio de distribución. Con este contexto más amplio en mente, discutiré nuestro trabajo reciente (ver el documento aquí y el código aquí), en el que proponemos una formulación del problema que llamamos minimización de los riesgos de adaptacióno ARM.
Buceo en el turno de distribución
La gran mayoría de los trabajos en el aprendizaje de la máquina sigue el marco canónico de minimización del riesgo empírico…o ERM. Los métodos ERM asumen que no hay un cambio de distribución, por lo que la distribución de la prueba coincide exactamente con la distribución del entrenamiento. Esta suposición simplifica el desarrollo y el análisis de los poderosos métodos de aprendizaje de la máquina pero, como se ha discutido anteriormente, se viola rutinariamente en las aplicaciones del mundo real. Para ir más allá del ERM y aprender modelos que generalizan ante el cambio de distribución, debemos introducir supuestos adicionales. Sin embargo, debemos elegir cuidadosamente estos supuestos de manera que sigan siendo realistas y ampliamente aplicables.
¿Cómo mantenemos el realismo y la aplicabilidad? Una respuesta es modelar las suposiciones sobre las condiciones que los sistemas de aprendizaje automático enfrentan en el mundo real. Por ejemplo, en el entorno de ERM, los modelos se evalúan en cada punto de prueba uno a uno, pero en el mundo real, estos puntos de prueba están a menudo disponibles secuencialmente o en lotes. Para la transcripción de la escritura a mano, por ejemplo, podemos imaginarnos la recopilación de frases y párrafos enteros de los nuevos usuarios. Si hay un cambio en la distribución, la observación de múltiples puntos de prueba puede ser útil ya sea para inferir la distribución de prueba o para adaptar el modelo a esta nueva distribución, incluso en ausencia de etiquetas.
Muchos métodos recientes que utilizan este supuesto pueden clasificarse como adaptación del tiempo de pruebaincluyendo la normalización de los lotes, la estimación del cambio de etiqueta, la predicción de la rotación, la minimización de la entropía y más. A menudo, estos métodos incorporan fuertes sesgos inductivos que permiten una adaptación útil; por ejemplo, la predicción de la rotación está bien alineada con muchas tareas de clasificación de imágenes. Pero estos métodos generalmente proponen procedimientos de entrenamiento heurístico o no consideran en absoluto el procedimiento de entrenamiento, basándose en cambio en modelos preentrenados. Esto plantea la siguiente pregunta: ¿puede mejorarse la adaptación del tiempo de prueba mediante un mejor entrenamiento, de manera que el modelo pueda hacer un mejor uso del procedimiento de adaptación?
Podemos comprender esta cuestión investigando otros marcos destacados para manejar el cambio de distribución y, en particular, las suposiciones que estos marcos hacen. En las aplicaciones del mundo real, los datos de entrenamiento generalmente no consisten sólo en pares de etiquetas de entrada; en cambio, hay meta-datos asociado a cada ejemplo, como la hora y el lugar, o el usuario particular en el ejemplo de la escritura. Estos metadatos pueden utilizarse para organizar los datos de capacitación en grupos, y una suposición común en varios marcos es que los desplazamientos de la distribución del tiempo de prueba representan o bien nuevas distribuciones de grupos o bien nuevos grupos en conjunto. Esta suposición sigue permitiendo una amplia gama de cambios de distribución realistas y ha impulsado el desarrollo de numerosos métodos prácticos.
Por ejemplo, adaptación del dominio Los métodos suelen suponer el acceso a dos grupos de capacitación: los datos de origen y los de destino, y estos últimos se extraen de la distribución de la prueba. Así pues, estos métodos aumentan la capacitación para centrarse en la distribución del objetivo, por ejemplo mediante la ponderación de la importancia o el aprendizaje de representaciones invariables. Los métodos para grupo distributivamente robusto optimización y dominio generalización no asumen directamente el acceso a los datos de la distribución de la prueba, sino que utilizan los datos extraídos de múltiples grupos de capacitación para aprender un modelo que generalice en el momento de la prueba a nuevos grupos (o nuevas distribuciones de grupo). Así pues, estos trabajos previos se han centrado en gran medida en el procedimiento de capacitación y, en general, no se adaptan en el momento de la prueba (a pesar de la denominación «adaptación de dominio»).
Combinando el entrenamiento y los supuestos de prueba
Los marcos previos para el cambio de distribución han asumido grupos de capacitación o lotes de prueba, pero no tenemos conocimiento de ningún trabajo previo que utilice ambos supuestos. En nuestro trabajo, demostramos que es precisamente esta conjunción la que nos permite aprender a adaptarse para probar el cambio de distribución del tiempo, simulando tanto el cambio como el procedimiento de adaptación en el momento de la formación. De esta manera, nuestro marco puede ser entendido como un meta-aprendizaje y remitimos a los lectores interesados a esta entrada del blog para una visión detallada del meta-aprendizaje.
Minimización del riesgo de adaptación
Nuestro trabajo propone la minimización adaptativa de riesgos, o ARM, que es un establecimiento de problemas y objetivos que hace uso de ambos grupos en el momento de la formación y de los lotes en el momento de la prueba. Esta síntesis proporciona una respuesta general y de principios, a través de la lente del meta-aprendizaje, a la pregunta de cómo entrenar para la adaptación del tiempo de prueba. En particular, se meta-tren el modelo que utiliza cambios de distribución simulados, que es habilitado por los grupos de entrenamiento, de tal manera que exhibe fuertes después de la adaptación rendimiento en cada turno. Por lo tanto, el modelo aprende directamente cómo aprovechar mejor el procedimiento de adaptación, que luego ejecuta de la misma manera en el momento de la prueba. Si podemos identificar qué turnos de distribución de prueba son probables, como ver los datos de los nuevos usuarios finales, entonces podemos construir mejor los turnos de entrenamiento simulados, como el muestreo de datos de un solo usuario de entrenamiento en particular.

El procedimiento de entrenamiento para optimizar el objetivo del ARM se ilustra en el gráfico de arriba. A partir de los datos de entrenamiento, tomamos muestras de diferentes lotes que simulan diferentes turnos de distribución de grupos. Un modelo de adaptación entonces tiene la oportunidad de adaptar los parámetros del modelo usando los ejemplos no etiquetados. Esto nos permite meta-entrenar el modelo para el rendimiento post-adaptación realizando directamente actualizaciones de gradientes tanto en el modelo como en el modelo de adaptación.
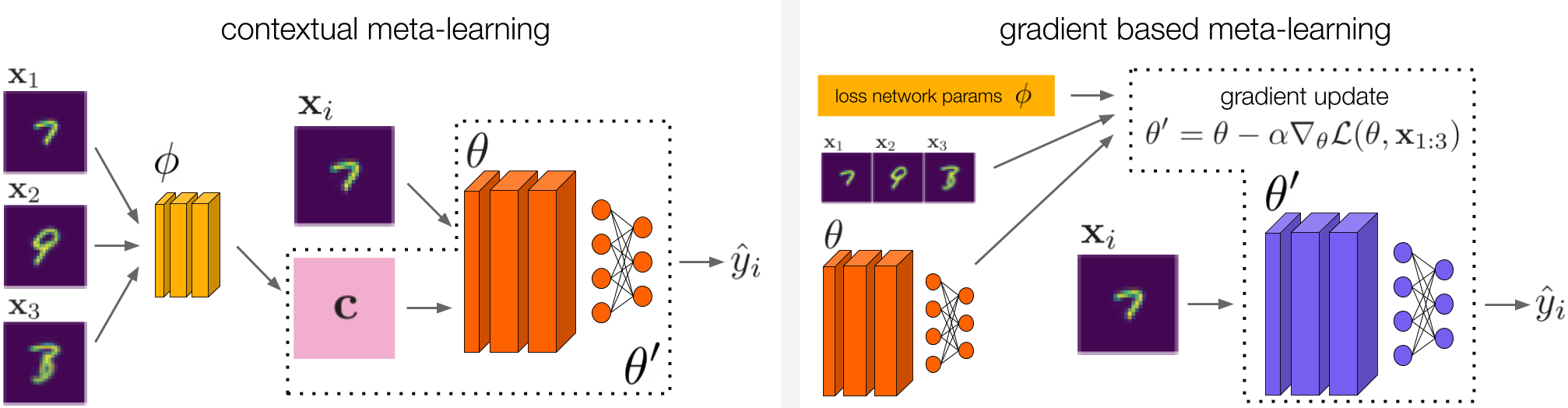
Nos inspiramos en el meta-aprendizaje contextual (izquierda) y en el meta-aprendizaje basado en el gradiente (derecha) para diseñar métodos para el ARM. Para el meta-aprendizaje contextual, investigamos dos métodos diferentes que entran en esta categoría. Estos métodos se describen en detalle en nuestro trabajo.
La conexión con el meta-aprendizaje es una ventaja clave del marco de trabajo de ARM, ya que no estamos empezando desde cero cuando ideamos métodos para resolver ARM. En nuestro trabajo en particular, nos inspiramos tanto en el meta-aprendizaje contextual como en el meta-aprendizaje basado en gradientes para desarrollar tres métodos para resolver los ARM, que denominamos ARM-CML, ARM-BN y ARM-LL. Omitimos los detalles de estos métodos aquí, pero están ilustrados en la figura anterior y descritos en su totalidad en nuestro trabajo.
La diversidad de métodos que construimos demuestra la versatilidad y la generalidad de la formulación del problema de los ARM. Pero, ¿observamos realmente ganancias empíricas utilizando estos métodos? A continuación investigamos esta pregunta.
Experimentos
En nuestros experimentos, primero realizamos un estudio exhaustivo de los métodos ARM propuestos en comparación con varias líneas de base, métodos anteriores y ablaciones, en cuatro puntos de referencia diferentes de clasificación de imágenes que muestran el cambio de distribución de grupos. Nuestro trabajo proporciona detalles completos sobre los puntos de referencia y las comparaciones.
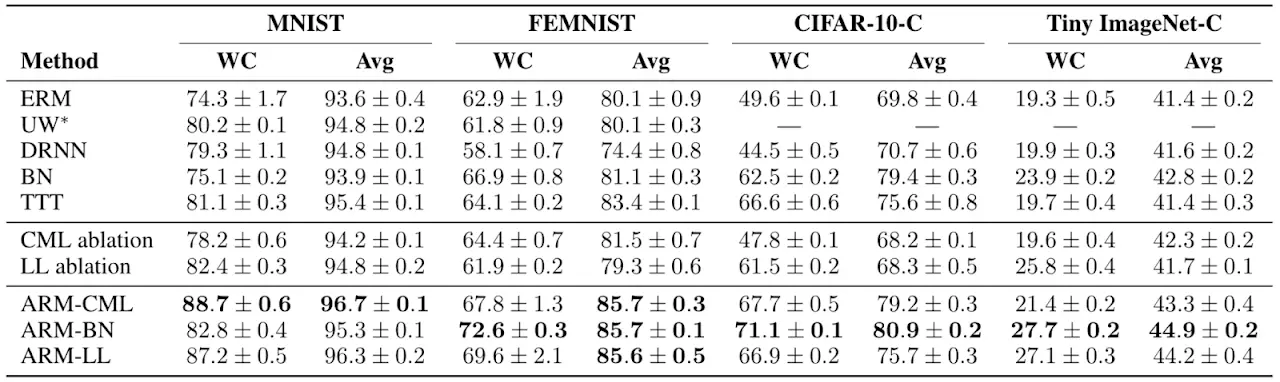
Encontramos que los métodos de ARM resultaron empíricamente tanto en un mejor rendimiento en el peor de los casos (WC) como en un rendimiento medio (Promedio) entre los grupos en comparación con los métodos anteriores, lo que indica tanto una mejor robustez como un mejor rendimiento de los modelos finales entrenados.
En nuestro estudio principal, encontramos que los métodos ARM tienen un mejor rendimiento en general, tanto en el peor de los casos como en el promedio de las pruebas en todos los grupos, en comparación con una serie de métodos anteriores junto con otras líneas de base y ablaciones. El método más simple de ARM-BN, que puede ser implementado en sólo unas pocas líneas de código adicional, a menudo se desempeñó mejor. Esto muestra empíricamente los beneficios del meta-aprendizaje, en el sentido de que el modelo puede ser meta-entrenado para aprovechar mejor el procedimiento de adaptación.

También realizamos algunos análisis cualitativos, en los que investigamos una situación de prueba similar al ejemplo motivador descrito al principio con un usuario que escribía a doble altura. Encontramos empíricamente que los modelos entrenados con los métodos ARM de hecho se adaptaban con éxito y predecían la «a» en esta situación, cuando se les daban suficientes ejemplos de la escritura del usuario que incluían otras «a» y «2». Así pues, esto confirma nuestra hipótesis original de que el entrenamiento de modelos adaptativos es una forma eficaz de hacer frente al cambio de distribución.
Creemos que el ejemplo motivador del principio, así como los resultados empíricos de nuestro trabajo, argumentan convincentemente a favor de un mayor estudio de las técnicas generales para modelos adaptativos. Hemos presentado un esquema general para el meta-entrenamiento de estos modelos para aprovechar mejor sus capacidades de adaptación, pero quedan varias cuestiones abiertas, como la elaboración de mejores procedimientos de adaptación en sí mismos. Esta amplia dirección de la investigación será crucial para que los modelos de aprendizaje de la máquina puedan realmente realizar su potencial en entornos complejos del mundo real.
Gracias a Chelsea Finn y Sergey Levine por darnos sus valiosos comentarios en este post.
Parte de este post se basa en el siguiente documento:
