Uso de circunvoluciones separables en profundidad en Tensorflow

Última actualización el 10 de agosto de 2022

Al observar todas las redes neuronales convolucionales muy grandes, como ResNets, VGG y similares, surge la pregunta de cómo podemos hacer que todas estas redes sean más pequeñas con menos parámetros y al mismo tiempo mantener el mismo nivel de precisión o incluso mejorar la generalización de el modelo usando una menor cantidad de parámetros. Un enfoque son las circunvoluciones separables en profundidad, también conocidas como circunvoluciones separables en TensorFlow y Pytorch (que no deben confundirse con las circunvoluciones espacialmente separables, que también se conocen como circunvoluciones separables). Sifre introdujo las circunvoluciones separables en profundidad en «Dispersión de movimiento rígido para la clasificación de imágenes» y han sido adoptadas por arquitecturas de modelos populares como MobileNet y una versión similar en Xception. Divide el canal y las circunvoluciones espaciales que generalmente se combinan en capas convolucionales normales.

En este tutorial, veremos qué son las circunvoluciones separables en profundidad y cómo podemos usarlas para acelerar nuestros modelos de imágenes de redes neuronales convolucionales.

Después de completar este tutorial, aprenderá:

¿Qué es una convolución separable en profundidad, puntual y en profundidad?
Cómo implementar circunvoluciones separables en profundidad en Tensorflow

Utilizándolos como parte de nuestros modelos de visión artificial.

¡Empecemos!

Uso de circunvoluciones separables en profundidad en Tensorflow
Foto de Arisa Chattasa. Algunos derechos reservados.

Visión general

Este tutorial se divide en 3 partes:

¿Qué es una convolución separable en profundidad?
¿Por qué son útiles?

Uso de circunvoluciones separables en profundidad en el modelo de visión por computadora

¿Qué es una convolución separable en profundidad?

Antes de profundizar en las circunvoluciones separables en profundidad, podría ser útil hacer un resumen rápido de las circunvoluciones. Las convoluciones en el procesamiento de imágenes es un proceso de aplicación de un núcleo sobre el volumen, donde hacemos una suma ponderada de los píxeles con los pesos como los valores de los núcleos. Visualmente de la siguiente manera:

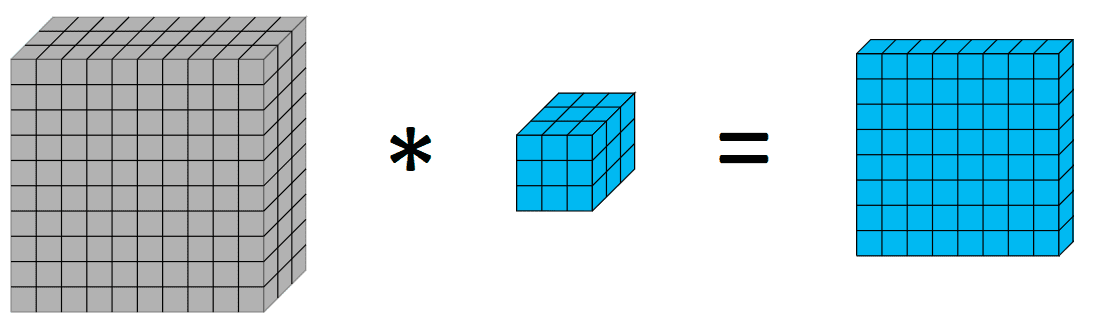
La aplicación de un kernel de 3 × 3 en un 10x10x3 genera un volumen de 8x8x1

Ahora, introduzcamos una convolución en profundidad. Una convolución en profundidad es básicamente una convolución a lo largo de una sola dimensión espacial de la imagen. Visualmente, así es como se vería y haría un único filtro convolucional en profundidad:

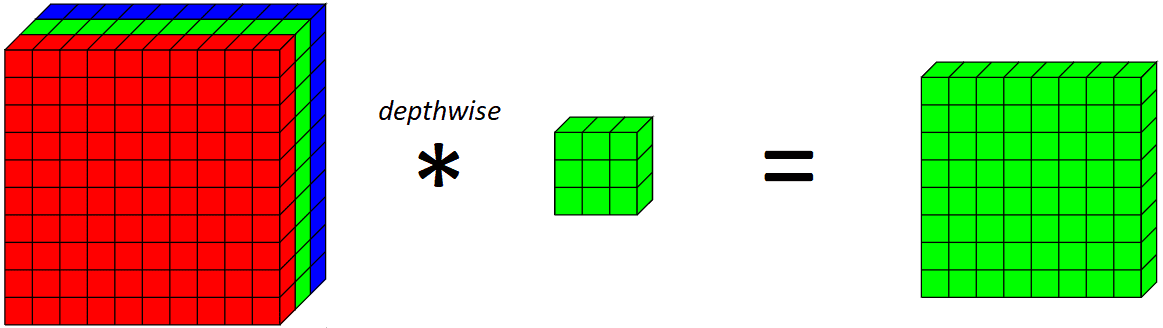
Aplicando una profundidad 3x3 kernel en el canal verde en este ejemplo

La diferencia clave entre una capa convolucional normal y una convolución en profundidad es que la convolución en profundidad aplica la convolución a lo largo de solo una dimensión espacial (es decir, el canal), mientras que una convolución normal se aplica en todas las dimensiones/canales espaciales en cada paso.

Si observamos lo que hace una capa completa en profundidad en todos los canales RGB,

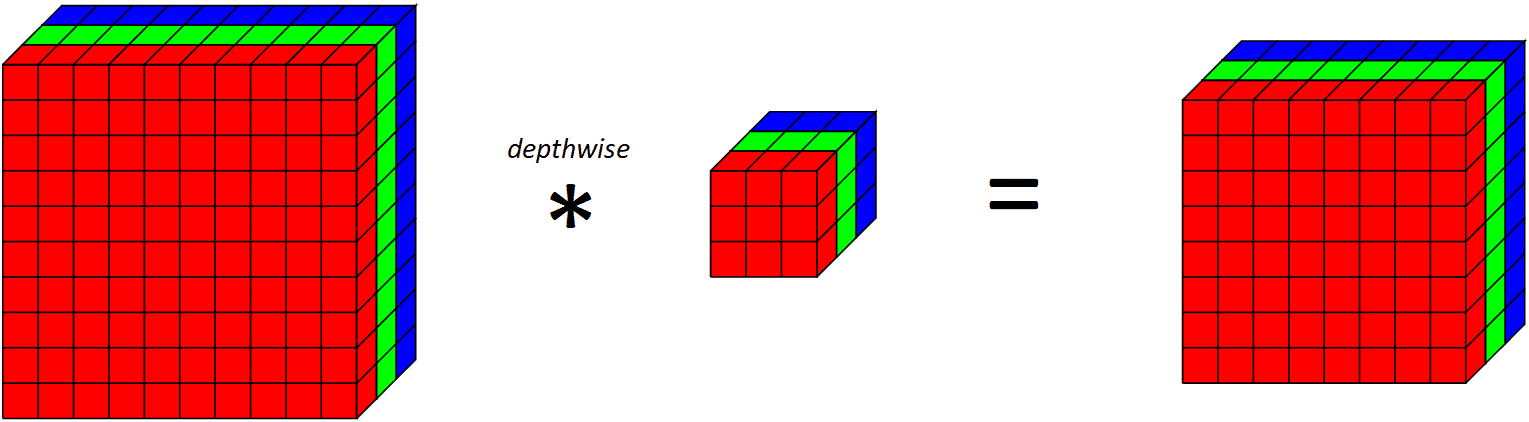
Aplicando un filtro convolucional en profundidad en 10x10x3 salidas de volumen de entrada 8x8x3 volumen

Tenga en cuenta que dado que estamos aplicando un filtro convolucional para cada canal de salida, la cantidad de canales de salida es igual a la cantidad de canales de entrada. Después de aplicar esta capa convolucional en profundidad, aplicamos una capa convolucional puntual.

En pocas palabras, una capa convolucional puntual es una capa convolucional regular con una 1x1 kernel (por lo tanto, mirando un solo punto en todos los canales). Visualmente, se ve así:

Aplicando una convolución puntual en un 10x10x3 el volumen de entrada emite un 10x10x1 volumen de salida

¿Por qué son útiles las circunvoluciones separables en profundidad?

Ahora, quizás se pregunte, ¿de qué sirve hacer dos operaciones con las circunvoluciones separables en profundidad? Dado que el título de este artículo es para acelerar los modelos de visión por computadora, ¿cómo hacer dos operaciones en lugar de una ayuda a acelerar las cosas?

Para responder a esa pregunta, echemos un vistazo a la cantidad de parámetros en el modelo (sin embargo, habría una sobrecarga adicional asociada con hacer dos circunvoluciones en lugar de una). Digamos que queremos aplicar 64 filtros convolucionales a nuestra imagen RGB para tener 64 canales en nuestra salida. El número de parámetros en la capa convolucional normal (incluido el término de polarización) es $ 3 times 3 times 3 times 64 + 64 = 1792$. Por otro lado, usar una capa convolucional separable en profundidad solo tendría $(3 times 3 times 1 times 3 + 3) + (1 times 1 times 3 times 64 + 64) = 30 + 256 = 286 $ parámetros, que es una reducción significativa, con convoluciones separables en profundidad que tienen menos de 6 veces los parámetros de la convolución normal.

Esto puede ayudar a reducir la cantidad de cálculos y parámetros, lo que reduce el tiempo de entrenamiento/inferencia y puede ayudar a regularizar nuestro modelo, respectivamente.

Veamos esto en acción. Para nuestras entradas, usemos el conjunto de datos de imagen CIFAR10 de 32x32x3 imágenes,

import tensorflow.keras as keras
from keras.datasets import mnist

# load dataset
(trainX, trainY), (testX, testY) = keras.datasets.cifar10.load_data()

Luego, implementamos una capa de convolución separable en profundidad. Hay una implementación en Tensorflow, pero la veremos en el ejemplo final.

class DepthwiseSeparableConv2D(keras.layers.Layer):
def __init__(self, filters, kernel_size, padding, activation):
super(DepthwiseSeparableConv2D, self).__init__()
self.depthwise = DepthwiseConv2D(kernel_size = kernel_size, padding = padding, activation = activation)
self.pointwise = Conv2D(filters = filters, kernel_size = (1, 1), activation = activation)

def call(self, input_tensor):
x = self.depthwise(input_tensor)
return self.pointwise(x)

Construyendo un modelo usando una capa convolucional separable en profundidad y observando la cantidad de parámetros,

visible = Input(shape=(32, 32, 3))
depthwise_separable = DepthwiseSeparableConv2D(filters=64, kernel_size=(3,3), padding=»valid», activation=»relu»)(visible)
depthwise_model = Model(inputs=visible, outputs=depthwise_separable)
depthwise_model.summary()

que da la salida

_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_15 (InputLayer) [(None, 32, 32, 3)] 0

depthwise_separable_conv2d_ (None, 30, 30, 64) 286
11 (DepthwiseSeparableConv2
D)

=================================================================
Total params: 286
Trainable params: 286
Non-trainable params: 0
_________________________________________________________________

que podemos comparar con un modelo similar usando una capa convolucional 2D regular,

normal = Conv2D(filters=64, kernel_size=(3,3), padding=”valid”, activation=”relu”)(visible)

que da la salida

conv2d (Conv2D) (None, 30, 30, 64) 1792

=================================================================
Total params: 1,792
Trainable params: 1,792
Non-trainable params: 0
_________________________________________________________________

Eso corrobora con nuestros cálculos iniciales sobre la cantidad de parámetros realizados anteriormente y muestra la reducción en la cantidad de parámetros que se puede lograr mediante el uso de convoluciones separables en profundidad.

Más específicamente, veamos el número y el tamaño de los núcleos en una capa convolucional normal y una separable en profundidad. Al observar una capa convolucional 2D regular con $c$ canales como entradas, $w times h$ resolución espacial del núcleo y $n$ canales como salida, necesitaríamos tener $(n, w, h, c)$ parámetros, es decir, $n$ filtros, y cada filtro tiene un tamaño de kernel de $(w, h, c)$. Sin embargo, esto es diferente para una convolución separable en profundidad similar incluso con el mismo número de canales de entrada, resolución espacial del kernel y canales de salida. Primero, está la convolución profunda que involucra filtros $c$, cada uno con un tamaño de kernel de $(w, h, 1)$ que genera canales $c$ ya que actúa en cada filtro. Esta capa convolucional en profundidad tiene parámetros $(c, w, h, 1)$ (más algunas unidades de polarización). Luego viene la convolución puntual que toma los canales $c$ de la capa de profundidad y genera $n$ canales, por lo que tenemos $n$ filtros, cada uno con un tamaño de kernel de $(1, 1, n)$. Esta capa convolucional puntual tiene parámetros $(n, 1, 1, n)$ (más algunas unidades de polarización).

Puede que estés pensando ahora mismo, pero ¿por qué funcionan?

Una forma de pensar al respecto, del artículo Xception de Chollet, es que las circunvoluciones separables en profundidad tienen la suposición de que podemos mapear por separado las correlaciones espaciales y de canales cruzados. Dado esto, habrá un montón de pesos redundantes en la capa convolucional que podemos reducir separando la convolución en dos convoluciones del componente de profundidad y de punto. Una forma de pensar sobre esto para aquellos familiarizados con el álgebra lineal es cómo podemos descomponer una matriz en el producto exterior de dos vectores cuando los vectores de columna en la matriz son múltiplos entre sí.

Uso de circunvoluciones separables en profundidad en modelos de visión artificial

Ahora que hemos visto la reducción en los parámetros que podemos lograr al usar una convolución separable en profundidad sobre un filtro convolucional normal, veamos cómo podemos usarlo en la práctica con Tensorflow. SeparableConv2D filtrar.

Para este ejemplo, utilizaremos el conjunto de datos de imagen CIFAR-10 utilizado en el ejemplo anterior, mientras que para el modelo utilizaremos un modelo construido a partir de bloques VGG. El potencial de las convoluciones separables en profundidad se encuentra en modelos más profundos, donde el efecto de regularización es más beneficioso para el modelo y la reducción de los parámetros es más obvia en comparación con un modelo más liviano como LeNet-5.

Creando nuestro modelo usando bloques VGG usando capas convolucionales normales,

from keras.models import Model
from keras.layers import Input, Conv2D, MaxPooling2D, Dense, Flatten, SeparableConv2D
import tensorflow as tf

# function for creating a vgg block
def vgg_block(layer_in, n_filters, n_conv):
# add convolutional layers
for _ in range(n_conv):
layer_in = Conv2D(filters = n_filters, kernel_size = (3,3), padding=’same’, activation=»relu»)(layer_in)
# add max pooling layer
layer_in = MaxPooling2D((2,2), strides=(2,2))(layer_in)
return layer_in

visible = Input(shape=(32, 32, 3))
layer = vgg_block(visible, 64, 2)
layer = vgg_block(layer, 128, 2)
layer = vgg_block(layer, 256, 2)
layer = Flatten()(layer)
layer = Dense(units=10, activation=»softmax»)(layer)

# create model
model = Model(inputs=visible, outputs=layer)

# summarize model
model.summary()

model.compile(optimizer=»adam», loss=tf.keras.losses.SparseCategoricalCrossentropy(), metrics=»acc»)

history = model.fit(x=trainX, y=trainY, batch_size=128, epochs=10, validation_data=(testX, testY))

Luego observamos los resultados de esta red neuronal convolucional de 6 capas con capas convolucionales normales,

conv2d (Conv2D) (None, 32, 32, 64) 1792

conv2d_1 (Conv2D) (None, 32, 32, 64) 36928

max_pooling2d (MaxPooling2D (None, 16, 16, 64) 0
)

conv2d_2 (Conv2D) (None, 16, 16, 128) 73856

conv2d_3 (Conv2D) (None, 16, 16, 128) 147584

max_pooling2d_1 (MaxPooling (None, 8, 8, 128) 0
2D)

conv2d_4 (Conv2D) (None, 8, 8, 256) 295168

conv2d_5 (Conv2D) (None, 8, 8, 256) 590080

max_pooling2d_2 (MaxPooling (None, 4, 4, 256) 0
2D)

flatten (Flatten) (None, 4096) 0

dense (Dense) (None, 10) 40970

=================================================================
Total params: 1,186,378
Trainable params: 1,186,378
Non-trainable params: 0
_________________________________________________________________
Epoch 1/10
391/391 [==============================] – 11s 27ms/step – loss: 1.7468 – acc: 0.4496 – val_loss: 1.3347 – val_acc: 0.5297
Epoch 2/10
391/391 [==============================] – 10s 26ms/step – loss: 1.0224 – acc: 0.6399 – val_loss: 0.9457 – val_acc: 0.6717
Epoch 3/10
391/391 [==============================] – 10s 26ms/step – loss: 0.7846 – acc: 0.7282 – val_loss: 0.8566 – val_acc: 0.7109
Epoch 4/10
391/391 [==============================] – 10s 26ms/step – loss: 0.6394 – acc: 0.7784 – val_loss: 0.8289 – val_acc: 0.7235
Epoch 5/10
391/391 [==============================] – 10s 26ms/step – loss: 0.5385 – acc: 0.8118 – val_loss: 0.7445 – val_acc: 0.7516
Epoch 6/10
391/391 [==============================] – 11s 27ms/step – loss: 0.4441 – acc: 0.8461 – val_loss: 0.7927 – val_acc: 0.7501
Epoch 7/10
391/391 [==============================] – 11s 27ms/step – loss: 0.3786 – acc: 0.8672 – val_loss: 0.8279 – val_acc: 0.7455
Epoch 8/10
391/391 [==============================] – 10s 26ms/step – loss: 0.3261 – acc: 0.8855 – val_loss: 0.8886 – val_acc: 0.7560
Epoch 9/10
391/391 [==============================] – 10s 27ms/step – loss: 0.2747 – acc: 0.9044 – val_loss: 1.0134 – val_acc: 0.7387
Epoch 10/10
391/391 [==============================] – 10s 26ms/step – loss: 0.2519 – acc: 0.9126 – val_loss: 0.9571 – val_acc: 0.7484

Probemos la misma arquitectura pero reemplacemos las capas convolucionales normales con las de Keras SeparableConv2D capas en su lugar:

# depthwise separable VGG block
def vgg_depthwise_block(layer_in, n_filters, n_conv):
# add convolutional layers
for _ in range(n_conv):
layer_in = SeparableConv2D(filters = n_filters, kernel_size = (3,3), padding=’same’, activation=’relu’)(layer_in)
# add max pooling layer
layer_in = MaxPooling2D((2,2), strides=(2,2))(layer_in)
return layer_in

visible = Input(shape=(32, 32, 3))
layer = vgg_depthwise_block(visible, 64, 2)
layer = vgg_depthwise_block(layer, 128, 2)
layer = vgg_depthwise_block(layer, 256, 2)
layer = Flatten()(layer)
layer = Dense(units=10, activation=»softmax»)(layer)
# create model
model = Model(inputs=visible, outputs=layer)

# summarize model
model.summary()

model.compile(optimizer=»adam», loss=tf.keras.losses.SparseCategoricalCrossentropy(), metrics=»acc»)

history_dsconv = model.fit(x=trainX, y=trainY, batch_size=128, epochs=10, validation_data=(testX, testY))

Ejecutar el código anterior nos da el resultado:

separable_conv2d (Separab (None, 32, 32, 64) 283
leConv2D)

separable_conv2d_2 (Separab (None, 32, 32, 64) 4736
leConv2D)

max_pooling2d (MaxPoolin (None, 16, 16, 64) 0
g2D)

separable_conv2d_3 (Separab (None, 16, 16, 128) 8896
leConv2D)

separable_conv2d_4 (Separab (None, 16, 16, 128) 17664
leConv2D)

max_pooling2d_2 (MaxPoolin (None, 8, 8, 128) 0
g2D)

separable_conv2d_5 (Separa (None, 8, 8, 256) 34176
bleConv2D)

separable_conv2d_6 (Separa (None, 8, 8, 256) 68096
bleConv2D)

max_pooling2d_3 (MaxPoolin (None, 4, 4, 256) 0
g2D)

flatten (Flatten) (None, 4096) 0

dense (Dense) (None, 10) 40970

=================================================================
Total params: 174,821
Trainable params: 174,821
Non-trainable params: 0
_________________________________________________________________
Epoch 1/10
391/391 [==============================] – 10s 22ms/step – loss: 1.7578 – acc: 0.3534 – val_loss: 1.4138 – val_acc: 0.4918
Epoch 2/10
391/391 [==============================] – 8s 21ms/step – loss: 1.2712 – acc: 0.5452 – val_loss: 1.1618 – val_acc: 0.5861
Epoch 3/10
391/391 [==============================] – 8s 22ms/step – loss: 1.0560 – acc: 0.6286 – val_loss: 0.9950 – val_acc: 0.6501
Epoch 4/10
391/391 [==============================] – 8s 21ms/step – loss: 0.9175 – acc: 0.6800 – val_loss: 0.9327 – val_acc: 0.6721
Epoch 5/10
391/391 [==============================] – 9s 22ms/step – loss: 0.7939 – acc: 0.7227 – val_loss: 0.8348 – val_acc: 0.7056
Epoch 6/10
391/391 [==============================] – 8s 22ms/step – loss: 0.7120 – acc: 0.7515 – val_loss: 0.8228 – val_acc: 0.7153
Epoch 7/10
391/391 [==============================] – 8s 21ms/step – loss: 0.6346 – acc: 0.7772 – val_loss: 0.7444 – val_acc: 0.7415
Epoch 8/10
391/391 [==============================] – 8s 21ms/step – loss: 0.5534 – acc: 0.8061 – val_loss: 0.7417 – val_acc: 0.7537
Epoch 9/10
391/391 [==============================] – 8s 21ms/step – loss: 0.4865 – acc: 0.8301 – val_loss: 0.7348 – val_acc: 0.7582
Epoch 10/10
391/391 [==============================] – 8s 21ms/step – loss: 0.4321 – acc: 0.8485 – val_loss: 0.7968 – val_acc: 0.7458

Tenga en cuenta que hay significativamente menos parámetros en la versión de convolución separable en profundidad (parámetros de ~200k frente a ~1,2 m), junto con un tiempo de tren ligeramente menor por época. Es más probable que las convoluciones separables en profundidad funcionen mejor en modelos más profundos que podrían enfrentar un problema de sobreajuste y en capas con núcleos más grandes, ya que hay una mayor disminución en los parámetros y cálculos que compensarían el costo computacional adicional de hacer dos convoluciones en lugar de una. A continuación, trazamos el tren, la validación y la precisión de los dos modelos para ver las diferencias en el rendimiento del entrenamiento de los modelos:

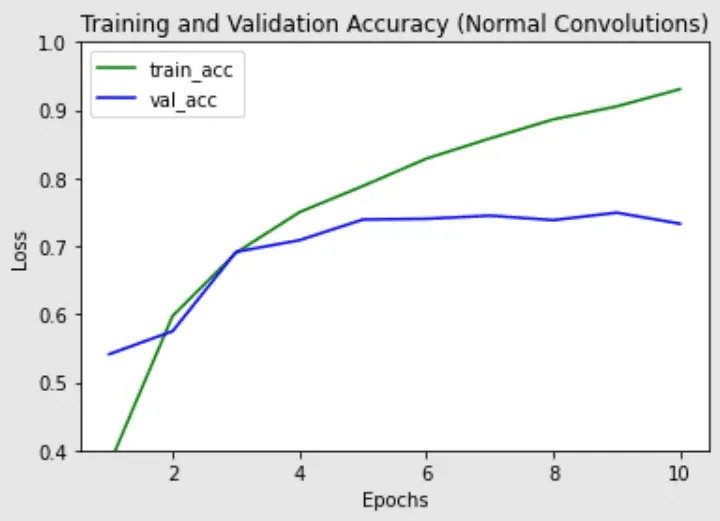
Precisión de entrenamiento y validación de la red con capas convolucionales normales

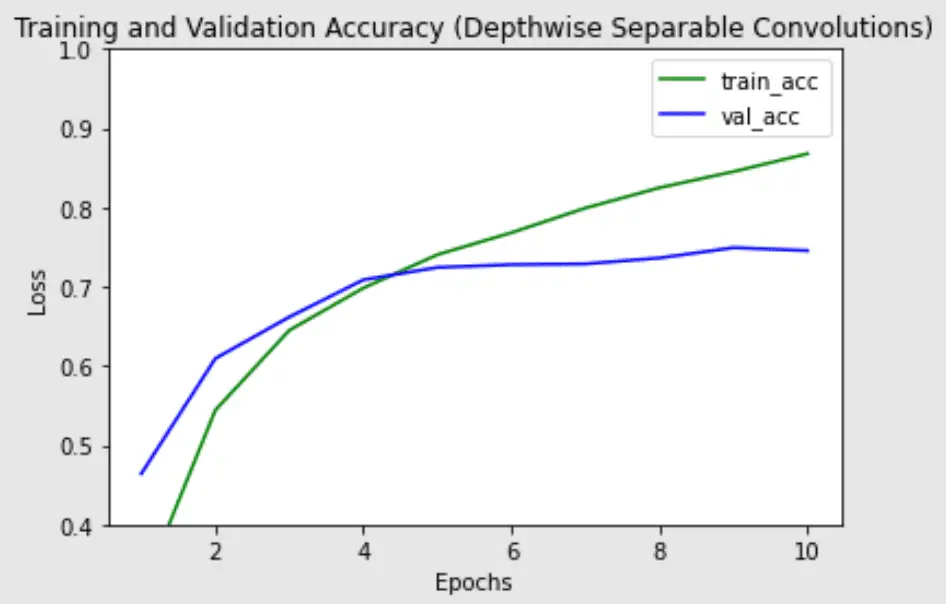
Precisión de entrenamiento y validación de la red con capas convolucionales separables en profundidad

La precisión de validación más alta es similar para ambos modelos, pero la convolución separable en profundidad parece tener menos sobreajuste en el conjunto de trenes, lo que podría ayudar a generalizar mejor los datos nuevos.

Combinando todo el código para la versión de circunvoluciones separables en profundidad del modelo,

import tensorflow.keras as keras
from keras.datasets import mnist

# load dataset
(trainX, trainY), (testX, testY) = keras.datasets.cifar10.load_data()
# depthwise separable VGG block
def vgg_depthwise_block(layer_in, n_filters, n_conv):
# add convolutional layers
for _ in range(n_conv):
layer_in = SeparableConv2D(filters = n_filters, kernel_size = (3,3), padding=’same’,activation=’relu’)(layer_in)
# add max pooling layer
layer_in = MaxPooling2D((2,2), strides=(2,2))(layer_in)
return layer_in

# summarize model
model.summary()

model.compile(optimizer=»adam», loss=tf.keras.losses.SparseCategoricalCrossentropy(), metrics=»acc»)

history_dsconv = model.fit(x=trainX, y=trainY, batch_size=128, epochs=10, validation_data=(testX, testY))

Otras lecturas

Esta sección proporciona más recursos sobre el tema si desea profundizar más.

Documentos:

Dispersión de movimiento rígido para la clasificación de imágenes (convoluciones separables en profundidad)
MobileNet

Xcepción

API:

Convoluciones separables en profundidad en Tensorflow (SeparableConv2D)

Resumen

En esta publicación, ha visto lo que son las circunvoluciones separables en profundidad, en puntos y en profundidad. También ha visto cómo el uso de circunvoluciones separables en profundidad nos permite obtener resultados competitivos mientras usamos una cantidad significativamente menor de parámetros.

En concreto, has aprendido:

¿Qué es una convolución separable en profundidad, puntual y en profundidad?

Cómo implementar circunvoluciones separables en profundidad en Tensorflow
Utilizándolos como parte de nuestros modelos de visión artificial.

La publicación Uso de circunvoluciones separables en profundidad en Tensorflow apareció primero en Machine Learning Mastery.