
Última actualización el 6 de agosto de 2021
El operador de Laplace fue aplicado por primera vez al estudio de la mecánica celeste, o el movimiento de objetos en el espacio exterior, por Pierre-Simon de Laplace, y como tal ha sido nombrado en su honor.
Desde entonces, el operador de Laplace se ha utilizado para describir muchos fenómenos diferentes, desde los potenciales eléctricos hasta la ecuación de difusión para el flujo de calor y fluidos, y la mecánica cuántica. También se ha vuelto a colocar en el espacio discreto, donde se ha utilizado en aplicaciones relacionadas con el procesamiento de imágenes y la agrupación espectral.
En este tutorial, descubrirás una suave introducción al laplaciano.
Después de completar este tutorial, sabrá:
- La definición del operador de Laplace y cómo se relaciona con la divergencia.
- Cómo se relaciona el operador de Laplace con el hessiano.
- Cómo el operador continuo de Laplace se ha vuelto a convertir en espacio discreto y se ha aplicado al procesamiento de imágenes y al agrupamiento espectral.
Empecemos.

Una suave introducción al laplaciano
Foto de Aziz Acharki, algunos derechos reservados.
Descripción general del tutorial
Este tutorial se divide en dos partes; ellos son:
- El laplaciano
- El concepto de divergencia
- El laplaciano continuo
- El laplaciano discreto
Prerrequisitos
Para este tutorial, asumimos que ya sabe cuáles son:
Puede revisar estos conceptos haciendo clic en los enlaces que se muestran arriba.
El laplaciano
El operador de Laplace (o laplaciano, como se le llama a menudo) es la divergencia del gradiente de una función.
Para comprender mejor el enunciado anterior, es mejor que comencemos por comprender el concepto de divergencia.
El concepto de divergencia
La divergencia es un operador vectorial que opera sobre un campo vectorial. Se puede pensar que este último representa un flujo de un líquido o gas, donde cada vector en el campo vectorial representa un vector de velocidad del fluido en movimiento.
En términos generales, la divergencia mide la tendencia del fluido a acumularse o dispersarse en un punto …
– Página 432, Cálculo simple y multivariable, 2020.
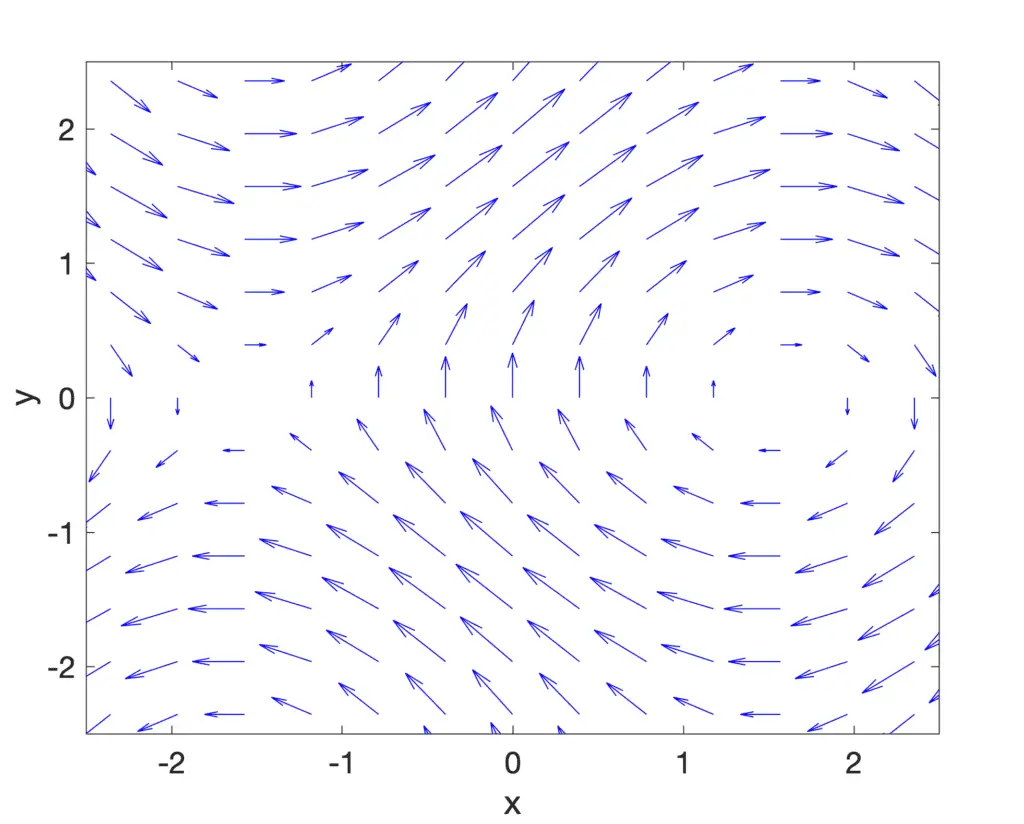
Parte del campo vectorial de (cos X, pecado y)
Usando el operador nabla (o del), ∇, la divergencia se denota por ∇ . y produce un valor escalar cuando se aplica a un campo vectorial, midiendo la cantidad de líquido en cada punto. En coordenadas cartesianas, la divergencia de un campo vectorial, F = ⟨F, gramo, h⟩, es dado por:
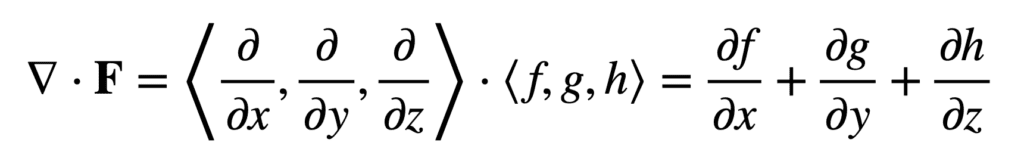
Aunque el cálculo de la divergencia implica la aplicación del operador de divergencia (en lugar de una operación de multiplicación), el punto en su notación recuerda al producto escalar, que implica la multiplicación de los componentes de dos secuencias de igual longitud (en este caso, ∇ y F) y la suma de los términos resultantes.
El laplaciano continuo
Volvamos a la definición de laplaciano.
Recuerde que el gradiente de una función bidimensional, F, es dado por:
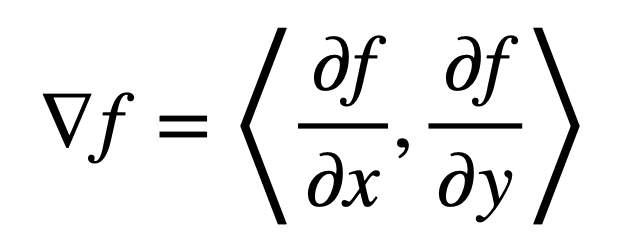
Entonces, el Laplaciano (es decir, la divergencia del gradiente) de F se puede definir por la suma de segundas derivadas parciales sin mezclar:
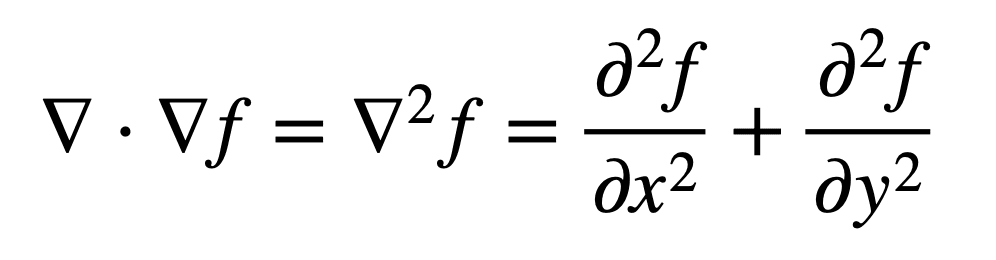
Puede, de manera equivalente, considerarse como la traza (tr) del hessiano de la función, H(F). La traza define la suma de los elementos en la diagonal principal de un cuadrado. norte×norte matriz, que en este caso es el hessiano, y también la suma de sus valores propios. Recuerde que la matriz de Hesse contiene las segundas derivadas parciales propias (o no mezcladas) en la diagonal:
![]()
Una propiedad importante de la traza de una matriz es su invariancia a cambio de base. Ya hemos definido el laplaciano en coordenadas cartesianas. En coordenadas polares, lo definiríamos de la siguiente manera:
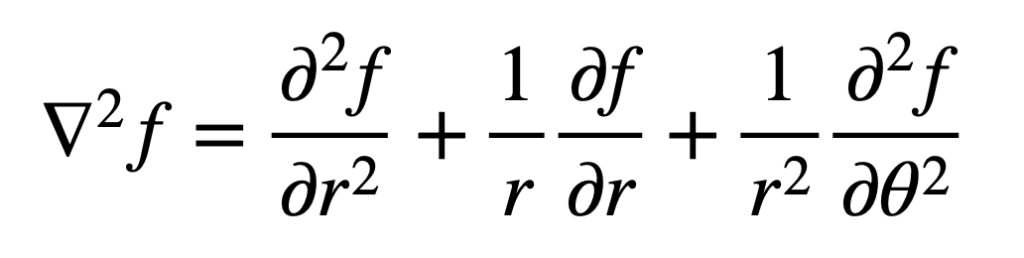
La invariancia de la traza a un cambio de base significa que el laplaciano se puede definir en diferentes espacios de coordenadas, pero daría el mismo valor en algún punto (X, y) en el espacio de coordenadas cartesianas, y en el mismo punto (r, θ) en el espacio de coordenadas polares.
Recuerde que también habíamos mencionado que la segunda derivada puede proporcionarnos información sobre la curvatura de una función. Por lo tanto, intuitivamente, podemos considerar que el laplaciano también nos proporciona información sobre la curvatura local de una función, a través de esta suma de segundas derivadas.
El operador continuo de Laplace se ha utilizado para describir muchos fenómenos físicos, como los potenciales eléctricos y la ecuación de difusión para el flujo de calor.
El laplaciano discreto
Análogo al operador continuo de Laplace, es el discreto, así formulado para ser aplicado a una cuadrícula discreta de, digamos, valores de píxeles en una imagen o en un gráfico.
Echemos un vistazo a cómo se puede reprogramar el operador de Laplace para ambas aplicaciones.
En el procesamiento de imágenes, el operador de Laplace se realiza en forma de un filtro digital que, cuando se aplica a una imagen, se puede utilizar para la detección de bordes. En cierto sentido, podemos considerar al operador laplaciano utilizado en el procesamiento de imágenes para, también, proporcionarnos información sobre la forma en que la función se curva (o curva). enfermedad de buzo) en algún punto en particular, (X, y).
En este caso, el operador (o filtro) discreto de Laplacia se construye combinando dos filtros de segunda derivada unidimensionales en uno solo bidimensional:
![]()
En el aprendizaje automático, la información proporcionada por el operador discreto de Laplace, derivada de un gráfico, se puede utilizar para la agrupación de datos.
Considere un gráfico, GRAMO = (V, mi), que tiene un número finito de V vértices y mi bordes. Su matriz laplaciana, L, se puede definir en términos de la matriz de grados, D, que contiene información sobre la conectividad de cada vértice y la matriz de adyacencia, A, que indica pares de vértices adyacentes en el gráfico:
L = D – A
La agrupación espectral se puede llevar a cabo aplicando algún método de agrupación estándar (como k-medios) en los vectores propios de la matriz laplaciana, por lo que se dividen los nodos del gráfico (o los puntos de datos) en subconjuntos.
Un problema que puede surgir al hacerlo se relaciona con un problema de escalabilidad con grandes conjuntos de datos, donde la descomposición propia (o la extracción de los vectores propios) de la matriz laplaciana puede ser prohibitiva. Se ha propuesto el uso del aprendizaje profundo para abordar este problema, donde se entrena una red neuronal profunda de modo que sus salidas se aproximen a los autovectores del grafo laplaciano. La red neuronal, en este caso, se entrena utilizando un enfoque de optimización restringido, para hacer cumplir la ortogonalidad de las salidas de la red.
Otras lecturas
Esta sección proporciona más recursos sobre el tema si desea profundizar.
Libros
Artículos
Documentos
Resumen
En este tutorial, descubrió una suave introducción al laplaciano.
Específicamente, aprendiste:
- La definición del operador de Laplace y cómo se relaciona con la divergencia.
- Cómo se relaciona el operador de Laplace con el hessiano.
- Cómo el operador continuo de Laplace se ha vuelto a convertir en espacio discreto y se ha aplicado al procesamiento de imágenes y al agrupamiento espectral.
¿Tiene usted alguna pregunta?
Haga sus preguntas en los comentarios a continuación y haré todo lo posible para responder.
