
Última actualización el 12 de agosto de 2020
La teoría del aprendizaje computacional, o teoría del aprendizaje estadístico, se refiere a los marcos matemáticos para cuantificar las tareas y algoritmos de aprendizaje.
Se trata de subcampos del aprendizaje automático que un practicante de aprendizaje automático no necesita conocer en gran profundidad para lograr buenos resultados en una amplia gama de problemas. No obstante, es un subcampo en el que tener una comprensión de alto nivel de algunos de los métodos más destacados puede proporcionar una visión de la tarea más amplia de aprender a partir de los datos.
En este post, descubrirán una suave introducción a la teoría de aprendizaje computacional para el aprendizaje de las máquinas.
Después de leer este post, lo sabrás:
- La teoría del aprendizaje computacional utiliza métodos formales para estudiar las tareas de aprendizaje y los algoritmos de aprendizaje.
- El aprendizaje del PAC proporciona una forma de cuantificar la dificultad computacional de una tarea de aprendizaje de la máquina.
- VC Dimension proporciona una forma de cuantificar la capacidad de cálculo de un algoritmo de aprendizaje de una máquina.
Empecemos.

Una suave introducción a la teoría del aprendizaje computacional
Foto de alguien10x, algunos derechos reservados.
Resumen del Tutorial
Este tutorial está dividido en tres partes; son:
- Teoría del Aprendizaje Computacional
- Aprendizaje PAC (Teoría de los Problemas de Aprendizaje)
- Dimensión VC (Teoría de Algoritmos de Aprendizaje)
Teoría del Aprendizaje Computacional
Teoría de aprendizaje computacional, o CoLT para abreviar, es un campo de estudio que se ocupa del uso de métodos matemáticos formales aplicados a los sistemas de aprendizaje.
Busca utilizar las herramientas de la informática teórica para cuantificar los problemas de aprendizaje. Esto incluye la caracterización de la dificultad de aprendizaje de tareas específicas.
La teoría de aprendizaje computacional puede ser pensada como una extensión o hermano de la teoría de aprendizaje estadístico, o SLT para abreviar, que utiliza métodos formales para cuantificar los algoritmos de aprendizaje.
- Teoría del Aprendizaje Computacional (CoLT): Estudio formal de las tareas de aprendizaje.
- Teoría Estadística del Aprendizaje (SLT): Estudio formal de los algoritmos de aprendizaje.
Esta división de las tareas de aprendizaje vs. los algoritmos de aprendizaje es arbitraria, y en la práctica, hay mucho solapamiento entre los dos campos.
Se puede ampliar la teoría del aprendizaje estadístico teniendo en cuenta la complejidad computacional del alumno. Este campo se llama teoría de aprendizaje computacional o COLT.
– Página 210, Aprendizaje automático: Una Perspectiva Probabilística, 2012.
Podrían considerarse sinónimos en el uso moderno.
…un marco teórico conocido como teoría de aprendizaje computacional, también llamada teoría de aprendizaje estadístico.
– Página 344, Pattern Recognition and Machine Learning, 2006.
El enfoque de la teoría de aprendizaje computacional es típicamente en tareas de aprendizaje supervisadas. El análisis formal de los problemas reales y los algoritmos reales es muy desafiante. Por ello, es común reducir la complejidad del análisis centrándose en tareas de clasificación binaria e incluso en sistemas binarios simples basados en reglas. Como tal, la aplicación práctica de los teoremas puede ser limitada o difícil de interpretar para problemas y algoritmos reales.
La principal pregunta sin respuesta en el aprendizaje es esta: ¿Cómo podemos estar seguros de que nuestro algoritmo de aprendizaje ha producido una hipótesis que predecirá el valor correcto de entradas no vistas anteriormente?
– Página 713, Inteligencia Artificial: Un enfoque moderno, 3ª edición, 2009.
Las preguntas exploradas en la teoría del aprendizaje computacional podrían incluir:
- ¿Cómo sabemos que un modelo tiene una buena aproximación para la función del objetivo?
- ¿Qué espacio de hipótesis debe utilizarse?
- ¿Cómo sabemos si tenemos una buena solución local o global?
- ¿Cómo evitamos el exceso de equipamiento?
- ¿Cuántos ejemplos de datos se necesitan?
Como practicante de aprendizaje de máquinas, puede ser útil conocer la teoría del aprendizaje computacional y algunas de las principales áreas de investigación. El campo proporciona una base útil para lo que estamos tratando de lograr al ajustar los modelos en los datos, y puede proporcionar una visión de los métodos.
Hay muchos subcampos de estudio, aunque quizás dos de las áreas de estudio más discutidas de la teoría del aprendizaje computacional son:
- Aprendizaje PAC.
- Dimensión VC.
En pocas palabras, podemos decir que el Aprendizaje PAC es la teoría de los problemas de aprendizaje de las máquinas y la dimensión VC es la teoría de los algoritmos de aprendizaje de las máquinas.
Es posible que se encuentre con los temas como practicante y es útil tener una idea en miniatura de lo que se trata. Echemos un vistazo más de cerca a cada uno.
Si quiere profundizar en el campo de la teoría del aprendizaje computacional, le recomiendo el libro:
Aprendizaje PAC (Teoría de los Problemas de Aprendizaje)
La probabilidad de un aprendizaje aproximadamente correcto, o aprendizaje PAC, se refiere a un marco teórico de aprendizaje de la máquina desarrollado por Leslie Valiant.
El aprendizaje PAC busca cuantificar la dificultad de una tarea de aprendizaje y podría considerarse el principal subcampo de la teoría del aprendizaje computacional.
Considere que en el aprendizaje supervisado, estamos tratando de aproximar una función cartográfica subyacente desconocida de las entradas a las salidas. No sabemos cómo es esta función cartográfica, pero sospechamos que existe, y tenemos ejemplos de datos producidos por la función.
El aprendizaje de la PAC se refiere a cuánto esfuerzo computacional se requiere para encontrar una hipótesis (modelo de ajuste) que se aproxime a la función objetivo desconocida.
Para más información sobre el uso de «hipótesis» en el aprendizaje de la máquina para referirse a un modelo de ajuste, ver el tutorial:
La idea es que una mala hipótesis se descubrirá en base a las predicciones que haga sobre nuevos datos, por ejemplo, en base a su error de generalización.
Una hipótesis que consigue que la mayoría o un gran número de predicciones sean correctas, por ejemplo, que tenga un pequeño error de generalización, es probablemente una buena aproximación para la función objetivo.
El principio subyacente es que cualquier hipótesis que sea gravemente errónea se «descubrirá» casi con toda seguridad con una alta probabilidad después de un pequeño número de ejemplos, porque hará una predicción incorrecta. Por lo tanto, es poco probable que cualquier hipótesis que sea coherente con un conjunto suficientemente grande de ejemplos de entrenamiento sea seriamente errónea: es decir, TELEMENTE debe ser probablemente aproximadamente correcta.
– Página 714, Inteligencia Artificial: Un enfoque moderno, 3ª edición, 2009.
Este lenguaje probabilístico le da al teorema su nombre: «probabilidad aproximadamente correcta.” Es decir, una hipótesis busca «aproximado» una función de objetivo y es «probablemente» bueno si tiene un bajo error de generalización.
Un algoritmo de aprendizaje de PAC se refiere a un algoritmo que devuelve una hipótesis que es PAC.
Utilizando métodos formales, se puede especificar un error mínimo de generalización para una tarea de aprendizaje supervisada. El teorema puede utilizarse entonces para estimar el número esperado de muestras del dominio del problema que se necesitarían para determinar si una hipótesis es PAC o no. Es decir, proporciona una forma de estimar el número de muestras necesarias para encontrar una hipótesis PAC.
El objetivo del marco de la PAC es comprender cuán grande debe ser un conjunto de datos para poder dar una buena generalización. También da límites para el costo computacional del aprendizaje…
– Página 344, Pattern Recognition and Machine Learning, 2006.
Además, un espacio de hipótesis (algoritmo de aprendizaje de la máquina) es eficiente bajo el marco del PAC si un algoritmo puede encontrar una hipótesis PAC (modelo de ajuste) en tiempo polinomial.
Se dice que un espacio de hipótesis es eficientemente PAC-aprendible si hay un algoritmo de tiempo polinomial que puede identificar una función que es PAC.
– Página 210, Aprendizaje automático: Una Perspectiva Probabilística, 2012.
Para más información sobre el aprendizaje del PAC, consulte el libro seminal sobre el tema titulado:
Dimensión VC (Teoría de Algoritmos de Aprendizaje)
La teoría Vapnik-Chervonenkis, o la teoría VC para abreviar, se refiere a un marco teórico de aprendizaje de la máquina desarrollado por Vladimir Vapnik y Alexey Chervonenkis.
El aprendizaje de la teoría del CV busca cuantificar la capacidad de un algoritmo de aprendizaje y podría considerarse el principal subcampo de la teoría estadística del aprendizaje.
La teoría de la CV está compuesta por muchos elementos, entre los que destaca la dimensión de la CV.
La dimensión de la CV cuantifica la complejidad de un espacio de hipótesis, por ejemplo, los modelos que podrían encajar dados un algoritmo de representación y aprendizaje.
Una forma de considerar la complejidad de un espacio de hipótesis (espacio de modelos que podrían encajar) se basa en el número de hipótesis distintas que contiene y tal vez en cómo se podría navegar por el espacio. La dimensión VC es un enfoque inteligente que, en cambio, mide el número de ejemplos del problema objetivo que pueden ser discriminados por las hipótesis en el espacio.
La dimensión VC mide la complejidad de la hipótesis del espacio […] por el número de instancias distintas de X que pueden ser completamente discriminadas usando H.
– Página 214, Machine Learning, 1997.
La dimensión de la CV estima la capacidad o la habilidad del algoritmo de aprendizaje de una máquina de clasificación para un conjunto de datos específico (número y dimensionalidad de los ejemplos).
Formalmente, la dimensión de la CV es el mayor número de ejemplos del conjunto de datos de entrenamiento que el espacio de hipótesis del algoritmo puede «destrozar.”
La dimensión Vapnik-Chervonenkis, VC(H), del espacio hipotético H definido sobre el espacio de instancia X es el tamaño del mayor subconjunto finito de X destrozado por H.
– Página 215, Machine Learning, 1997.
La rotura o un conjunto de roturas, en el caso de un conjunto de datos, significa que los puntos del espacio de los rasgos pueden seleccionarse o separarse unos de otros utilizando hipótesis en el espacio de manera que las etiquetas de los ejemplos en los grupos separados sean correctas (sea lo que sea).
El que un grupo de puntos pueda ser destrozado por un algoritmo depende del espacio de la hipótesis y del número de puntos.
Por ejemplo, una línea (espacio de hipótesis) puede ser usada para romper tres puntos, pero no cuatro puntos.
Cualquier colocación de tres puntos en un plano 2d con etiquetas de clase 0 o 1 puede ser «correctamente» dividido por la etiqueta con una línea, por ejemplo, destrozado. Pero, existen colocaciones de cuatro puntos en el plano con etiquetas de clase binaria que no pueden ser correctamente divididas por etiqueta con una línea, por ejemplo no pueden ser destrozadas. En su lugar, se debe utilizar otro «algoritmo», como los óvalos.
La siguiente figura lo deja claro.
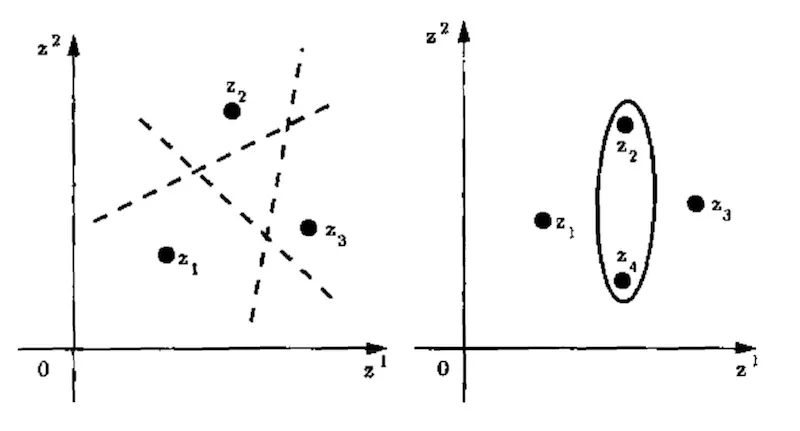
Ejemplo de una hipótesis de línea que rompe 3 puntos y ovalos que rompen 4 puntos
Tomado de la página 81, La naturaleza de la teoría del aprendizaje estadístico, 1999.
Por lo tanto, la dimensión de CV de un algoritmo de aprendizaje de una máquina es el mayor número de puntos de datos de un conjunto de datos que una configuración específica del algoritmo (hiperparámetros) o un modelo de ajuste específico puede destrozar.
Un clasificador que predice el mismo valor en todos los casos tendrá una dimensión VC de 0, sin puntos. Una dimensión VC grande indica que un algoritmo es muy flexible, aunque la flexibilidad puede venir a costa de un riesgo adicional de sobreajuste.
La dimensión de la CV se utiliza como parte del marco de aprendizaje de la PAC.
Una cantidad clave en el aprendizaje del PAC es la dimensión Vapnik-Chervonenkis, o dimensión VC, que proporciona una medida de la complejidad de un espacio de funciones, y que permite que el marco del PAC se extienda a espacios que contienen un número infinito de funciones.
– Página 344, Pattern Recognition and Machine Learning, 2006.
