Publicación cruzada del blog DeepMind Safety.
En muchos problemas de aprendizaje por refuerzo, el objetivo es demasiado complejo para ser especificado procedimentalmente y, en cambio, se debe aprender una función de recompensa a partir de los datos del usuario. Sin embargo, ¿cómo puede saber si una función de recompensa aprendida realmente captura las preferencias del usuario? Nuestro método, Comparación invariante de política equivalente (EPIC), permite evaluar una función de recompensa calculando qué tan similar es a otras funciones de recompensa. EPIC se puede utilizar para comparar los algoritmos de aprendizaje de recompensas comparando las funciones de recompensa aprendidas con una recompensa real.
También se puede utilizar para validar las funciones de recompensa aprendidas antes de la implementación, comparándolas con las funciones de recompensa aprendidas a través de diferentes técnicas o fuentes de datos.
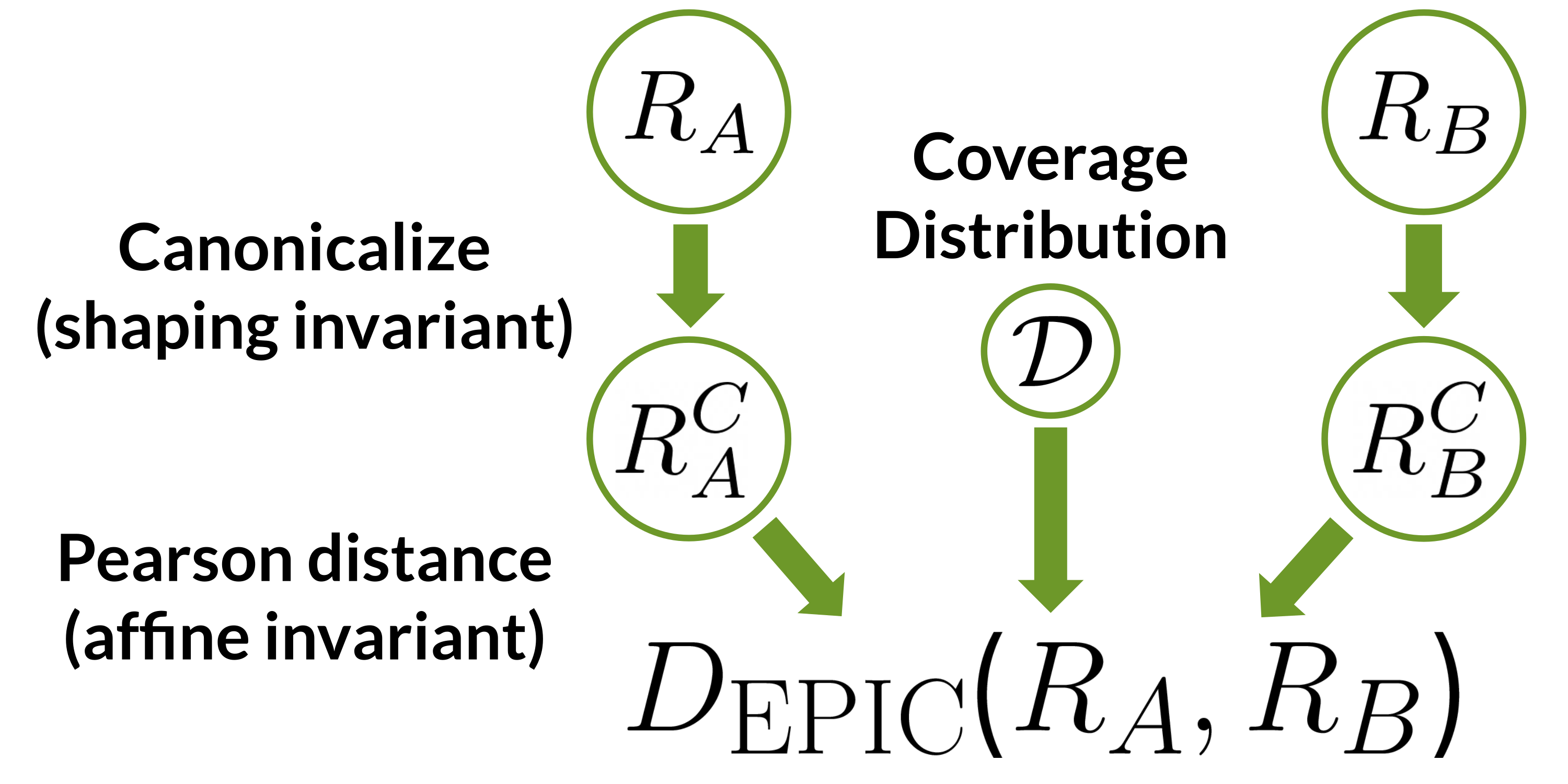
Figura 1: EPIC compara las funciones de recompensa $ R_a $ y $ R_b $ mapeándolas primero a representantes canónicos y luego calculando la distancia de Pearson entre los representantes canónicos en una distribución de cobertura $ mathcal {D} $. La canonicalización elimina el efecto de la conformación potencial, y la distancia de Pearson es invariante para las transformaciones afines positivas.
EPIC es hasta 1000 veces más rápido que los métodos de evaluación alternativos y requiere poco o ningún ajuste de hiperparámetros. Además, mostramos tanto teórica como empíricamente que las funciones de recompensa consideradas similares por EPIC inducen políticas con rendimientos similares, incluso en entornos invisibles.
Especificar una función de recompensa puede ser una de las partes más complicadas de aplicar RL a un problema. Incluso las tareas de robótica aparentemente simples, como la inserción de clavijas, pueden requerir primero entrenar a un clasificador de imágenes para usarlo como una señal de recompensa. Las tareas con un objetivo más nebuloso, como el resumen de artículos, requieren recopilar grandes cantidades de comentarios humanos para aprender una función de recompensa. La dificultad de la especificación de la función de recompensa solo seguirá creciendo a medida que RL se aplique cada vez más a aplicaciones complejas y orientadas al usuario, como sistemas de recomendación, chatbots y vehículos autónomos.
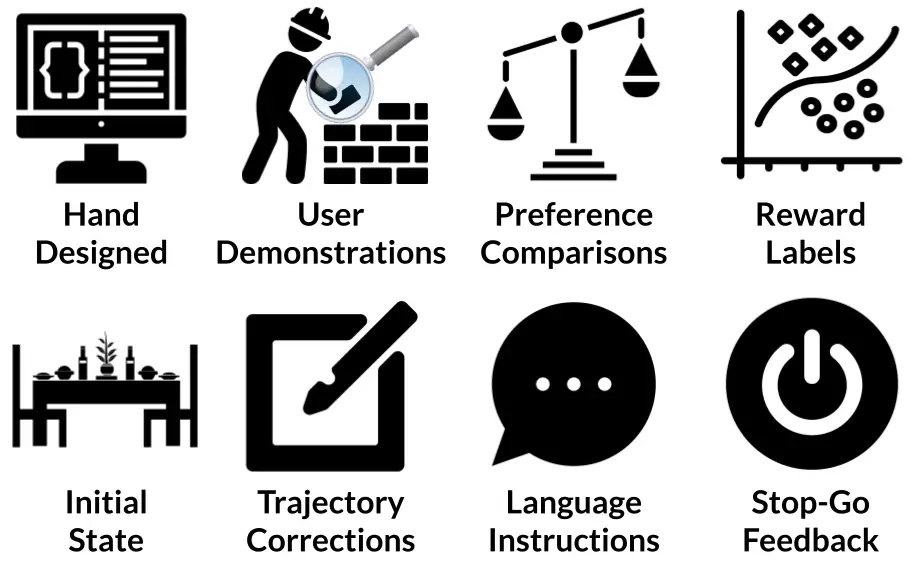
Figura 2: Existe una variedad de técnicas para especificar una función de recompensa. EPIC puede ayudarlo a decidir cuál funciona mejor para una tarea determinada.
Este desafío ha llevado al desarrollo de una variedad de métodos para especificar funciones de recompensa. Además de diseñar manualmente una función de recompensa, hoy es posible aprender una función de recompensa a partir de datos tan variados como el estado inicial, demostraciones, correcciones, comparaciones de preferencias y muchas otras fuentes de datos. Dada esta vertiginosa variedad de posibilidades, ¿cómo deberíamos elegir qué método utilizar?
EPIC es una nueva forma de evaluar las funciones de recompensa y los algoritmos de aprendizaje de recompensas comparando cómo las funciones de recompensa son similares entre sí. Anticipamos dos casos de uso principales para EPIC:
- Evaluación comparativa en tareas donde el problema de especificación de la función de recompensa ya ha sido resuelto, dando una recompensa de «verdad fundamental». Luego, podemos comparar las recompensas aprendidas directamente con esta «verdad fundamental» para medir el rendimiento de un nuevo método de aprendizaje de recompensas.
- Validación de las funciones de recompensa antes del despliegue. En particular, a menudo tenemos una colección de funciones de recompensa especificadas por diferentes personas, métodos o fuentes de datos. Si múltiples enfoques distintos producen funciones de recompensa similares (es decir, una distancia EPIC baja entre sí), entonces podemos tener más confianza en que la recompensa resultante es correcta. De manera más general, si dos funciones de recompensa tienen una distancia EPIC baja entre sí, la información que obtenemos sobre una (como mediante el uso de métodos de interpretación) también nos ayuda a comprender la otra.
Quizás sorprendentemente, no hay (a nuestro leal saber y entender) ningún trabajo previo que se centre en comparar directamente las funciones de recompensa. En cambio, la mayor parte del trabajo anterior ha utilizado RL para entrenar una política sobre recompensas aprendidas y luego evaluó las políticas resultantes. Desafortunadamente, el entrenamiento de RL es computacionalmente costoso. Además, no es confiable: si la política funciona mal, no podemos decir si esto se debe a que la recompensa aprendida no coincide con las preferencias del usuario o si el algoritmo RL no optimiza la recompensa aprendida.
Un problema más fundamental con la evaluación basada en el entrenamiento de RL es que dos recompensas pueden inducir políticas idénticas en un entorno de evaluación, pero llevar a un comportamiento totalmente diferente en el entorno de implementación. Suponga que todos los estados $ {X, Y, Z} $ son accesibles en el entorno de evaluación. Si el usuario prefiere $ X> Y> Z $, pero el agente aprende $ X> Z> Y $, el agente seguirá yendo al estado correcto $ X $ durante la evaluación. Pero si ya no se puede acceder a $ X $ en el momento de la implementación, el agente anteriormente confiable se comportaría mal yendo al estado menos favorecido $ Z $.
Por el contrario, EPIC es rápido, confiable y puede predecir el retorno incluso en entornos de implementación invisibles. Veamos cómo EPIC puede lograr esto.
Nuestro método, Comparación invariable de políticas equivalentes (EPIC), funciona comparando funciones de recompensa directamente, sin entrenar una política. Está diseñado para ser invariante a dos transformaciones que nunca cambian la política óptima:
- Modelado de potencial, que mueve la recompensa antes o después en el tiempo.
- Transformaciones afines positivas, agregando una constante o reescalando por un factor positivo.
EPIC se calcula en las dos etapas ilustradas en la Figura 1 (arriba), reflejando estos invariantes:
- Primero, canonicalizamos las recompensas que se comparan. Las recompensas que son iguales hasta la posible configuración se asignan al mismo representante canónico.
- A continuación, calculamos la correlación de Pearson entre los representantes canónicos, sobre alguna distribución de cobertura $ mathcal {D} $ sobre transiciones. La correlación de Pearson no varía con las transformaciones afines positivas.
Finalmente, transformamos la correlación, una medida de similitud, en una distancia.
EPIC satisface propiedades importantes que esperarías desde la distancia, a saber, la simetría y la desigualdad del triángulo. Esto le da a la distancia una interpretación intuitiva y permite que se utilice en algoritmos que se basan en funciones de distancia.
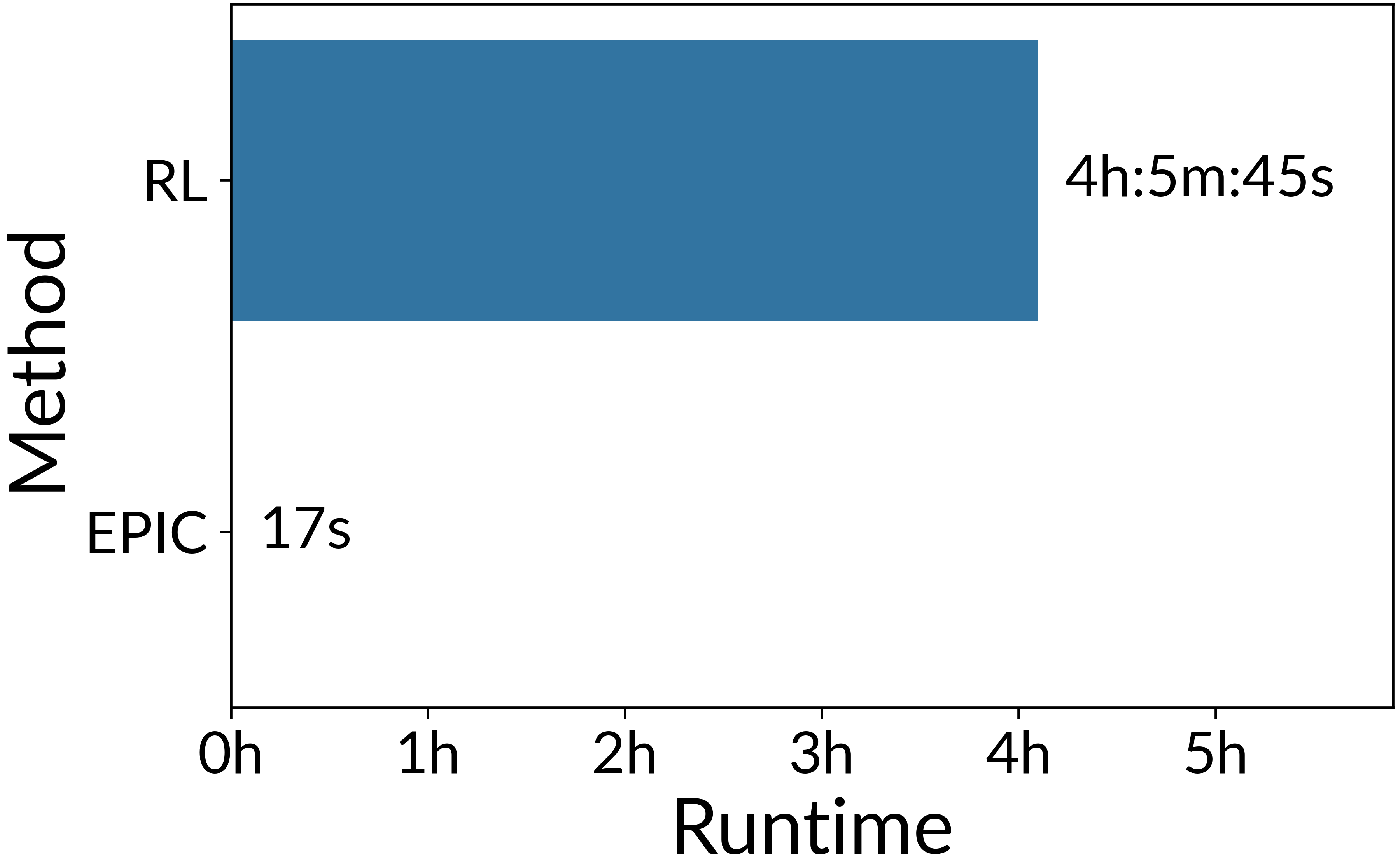
figura 3: Tiempo de ejecución necesario para realizar una comparación por pares de 5 funciones de recompensa en una simple tarea de control continuo.
Además, EPIC es más de 1000 veces más rápido que la comparación con el entrenamiento RL cuando se prueba en una tarea de control continuo de masa de puntos simple. También es fácil de usar: los únicos hiperparámetros que deben configurarse son la distribución de la cobertura y la cantidad de muestras que se deben tomar.
Un resultado teórico clave es que una distancia EPIC baja predice retornos de política similares. Específicamente, la distancia EPIC limita la diferencia en el rendimiento G de las políticas óptimas $ pi_A ^ ast $ y $ pi_B ^ ast $ para las recompensas $ R_A $ y $ R_B $ (ver Teorema 4.9):
donde $ K ( mathcal {D}) $ es una constante que depende del soporte de la distribución de cobertura EPIC. Este límite es válido para las políticas óptimas calculadas en cualquier MDP que tenga el mismo estado y espacios de acción que las recompensas $ R_A $ y $ R_B $. En ese sentido, EPIC ofrece una garantía de desempeño mucho más sólida que la evaluación de políticas en una sola instancia de una tarea.
Sin embargo, este resultado depende de que la distribución $ mathcal {D} $ tenga una cobertura adecuada sobre las transiciones visitadas por las pólizas óptimas $ pi_A ^ ast $ y $ pi_B ^ ast $. En general, recomendamos elegir $ mathcal {D} $ para tener cobertura en todas las transiciones plausibles. Esto asegura un soporte adecuado para $ pi_A ^ ast $ y $ pi_B ^ ast $, sin desperdiciar masa de probabilidad en transiciones físicamente imposibles que nunca ocurrirán.
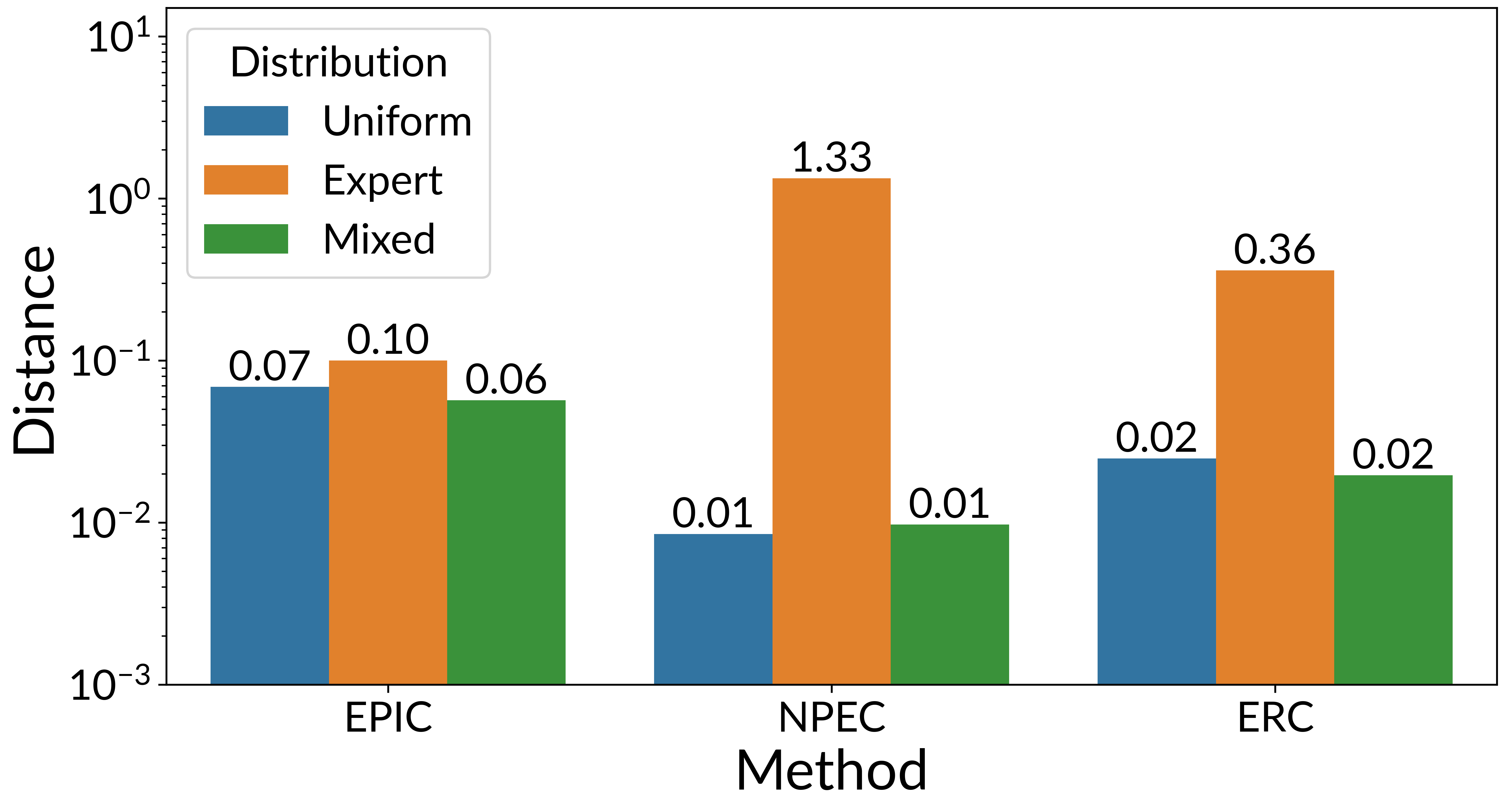
Figura 4:
La distancia EPIC entre recompensas es similar en diferentes distribuciones (barras de colores), mientras que las líneas de base (NPEC y ERC) son muy sensibles a la distribución. La distribución de cobertura consiste en lanzamientos de: una política que toma acciones uniformemente al azar, un experto política óptima y una mezclado política que cambia aleatoriamente entre los otros dos.
Si bien la garantía teórica de EPIC depende de la distribución de cobertura $ mathcal {D} $, encontramos que, en la práctica, EPIC es bastante robusto para la elección exacta de la distribución: una variedad de distribuciones razonables dan resultados similares. La figura anterior ilustra esto: EPIC (izquierda) calcula una distancia similar bajo diferentes distribuciones de cobertura (barras de colores), mientras que las líneas de base NPEC (centro) y ERC (derecha) exhiben una variación significativa.
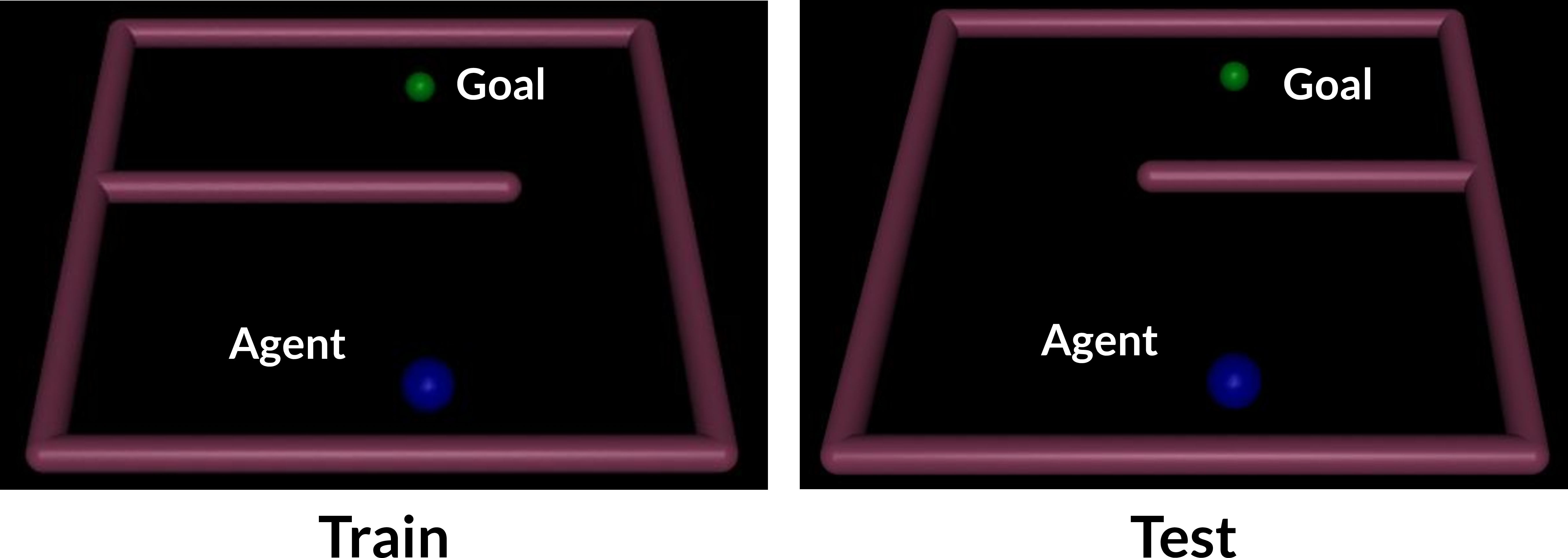
Figura 5:
El entorno de PointMaze: el agente debe alcanzar la meta navegando alrededor de la pared que está a la izquierda a la hora del tren y a la derecha a la hora de la prueba.
Incluso si la distancia es consistente en distribuciones de cobertura razonables, el factor constante $ K ( mathcal {D}) $ aún podría ser muy grande, haciendo que el límite sea débil o incluso vacío. Por lo tanto, decidimos probar empíricamente si la distancia EPIC predice el retorno de la política de RL, en una simple tarea de control continuo PointMaze. El agente debe navegar hacia una meta moviéndose alrededor de una pared que está a la izquierda durante el entrenamiento y a la derecha durante la prueba. La función de recompensa de la verdad fundamental es la misma en ambas variantes, por lo que podemos esperar que las funciones de recompensa aprendidas se transfieran. Tenga en cuenta que las políticas óptimas no se transfieren: la política óptima en el entorno del tren chocará con la pared cuando se implemente en el entorno de prueba, y viceversa.

Figura 6:
Distancia EPIC predice el arrepentimiento político en el entrenar y prueba tareas a través de tres métodos de aprendizaje de recompensa diferentes.
Entrenamos funciones de recompensa usando (a) regresión para recompensar etiquetas, (b) comparación de preferencias entre trayectorias y (c) aprendizaje por refuerzo inverso (IRL) en demostraciones. Los datos de entrenamiento se generan sintéticamente a partir de una recompensa basada en la verdad. Descubrimos que la regresión y la comparación de preferencias aprenden una función de recompensa con una distancia EPIC baja a la verdad del suelo. Las políticas entrenadas con estas recompensas logran un alto rendimiento y, por lo tanto, poco arrepentimiento. Por el contrario, IRL tiene una gran distancia EPIC al suelo, la verdad y el gran arrepentimiento. Esto está en línea con nuestro resultado teórico de que la distancia EPIC predice arrepentimiento.
Creemos que la distancia EPIC será una adición informativa a la caja de herramientas de evaluación para los métodos de aprendizaje de recompensa. EPIC es significativamente más rápido que el entrenamiento de RL y puede predecir el retorno de la póliza incluso en entornos invisibles. Por lo tanto, alentamos a los investigadores a informar sobre EPIC además de las métricas basadas en políticas al comparar los algoritmos de aprendizaje de recompensas.
Es importante que nuestra capacidad para especificar con precisión objetivos complejos siga el ritmo del crecimiento del poder de optimización del aprendizaje por refuerzo. Los futuros sistemas de IA, como los asistentes virtuales o los robots domésticos, operarán en entornos complejos y abiertos que implican una amplia interacción humana. Alcanzar el rendimiento a nivel humano en estos dominios requiere más que solo inteligencia a nivel humano: también debemos enseñar a nuestros sistemas de IA los muchos matices de los valores humanos. Esperamos que técnicas como EPIC jueguen un papel clave en la construcción de IA avanzada y alineada, al permitirnos evaluar diferentes modelos de valores humanos entrenados a través de múltiples técnicas o fuentes de datos.
En particular, creemos que EPIC puede mejorar significativamente la evaluación comparativa de los algoritmos de aprendizaje de recompensas. Al comparar directamente la recompensa aprendida con una recompensa real, EPIC puede proporcionar una medición precisa de la calidad de la función de recompensa, incluida su capacidad para transferirse a nuevos entornos. Por el contrario, el entrenamiento de RL no puede distinguir entre recompensas aprendidas que capturan las preferencias del usuario y aquellas que simplemente incentivan el comportamiento correcto en el entorno de evaluación (pero pueden fallar en otros entornos). Además, el entrenamiento de RL es lento y poco confiable.

Figura 7:
La evaluación realizada por el entrenamiento de RL concluye que la función de recompensa era defectuosa después destruyendo el jarrón. EPIC puede advertirle que la función de recompensa difiere de otras antes de entrena a un agente.
Además, EPIC puede ayudar a validar una función de recompensa antes de la implementación. El uso de EPIC es particularmente ventajoso en entornos donde las fallas son inaceptables, ya que EPIC puede comparar las funciones de recompensa fuera de línea en un conjunto de datos recopilados previamente. Por el contrario, el entrenamiento de RL requiere tomar acciones en el entorno para maximizar la nueva recompensa. Estas acciones podrían tener consecuencias irreversibles, como un robot doméstico que derriba un jarrón en el camino a la cocina si la recompensa aprendida incentiva la velocidad pero no penaliza los efectos secundarios negativos.
Sin embargo, EPIC tiene algunos inconvenientes, por lo que es mejor utilizarlo junto con otros métodos. Más significativamente, EPIC solo puede comparar funciones de recompensa entre sí, y no puede decirle qué valora una función de recompensa en particular. Dado un conjunto de funciones de recompensa desconocidas, en el mejor de los casos, EPIC puede agruparlas en grupos similares y diferentes. Se necesitarán otros métodos de evaluación, como la interpretabilidad o el entrenamiento de RL, para comprender lo que representa cada grupo.
Además, EPIC puede ser demasiado conservador. EPIC es, por diseño, sensible a las diferencias en las funciones de recompensa que podrían cambiar la política óptima, incluso si conducen al mismo comportamiento en el entorno de evaluación. Esto es deseable para aplicaciones críticas para la seguridad, donde la robustez del cambio de distribución es fundamental, pero esta misma propiedad puede generar falsas alarmas cuando el entorno de implementación es similar o idéntico al entorno de evaluación. Actualmente, la sensibilidad de EPIC a las diferencias fuera de distribución es controlable solo a un nivel de grano grueso utilizando la distribución de cobertura 𝒟. Una dirección prometedora para el trabajo futuro es admitir un control más detallado basado en distribuciones o invariantes en posibles entornos de implementación.
Consulte nuestro documento ICLR para obtener más información sobre EPIC. También puede encontrar una implementación de EPIC en GitHub.
Nos gustaría agradecer a Jonathan Uesato, Neel Nanda, Vladimir Mikulik, Sebastian Farquhar, Cody Wild, Neel Alex y Victoria Krakovna por sus comentarios sobre los borradores anteriores de esta publicación.
