Los algoritmos de clasificación aprenden a asignar etiquetas de clase a los ejemplos, aunque sus decisiones pueden parecer opacas.
Un diagnóstico popular para entender las decisiones tomadas por un algoritmo de clasificación es el superficie de decisión. Esta es una gráfica que muestra cómo un algoritmo de aprendizaje de una máquina de ajuste predice una cuadrícula gruesa a través del espacio de la característica de entrada.
Un gráfico de superficie de decisión es una herramienta poderosa para entender cómo un modelo dado «ve» la tarea de predicción y cómo ha decidido dividir el espacio de la característica de entrada por la etiqueta de la clase.
En este tutorial, descubrirá cómo trazar una superficie de decisión para un algoritmo de aprendizaje de una máquina de clasificación.
Después de completar este tutorial, lo sabrás:
- La superficie de decisión es una herramienta de diagnóstico para entender cómo un algoritmo de clasificación divide el espacio de características.
- Cómo trazar una superficie de decisión para usar etiquetas de clase nítidas para un algoritmo de aprendizaje de máquina.
- Cómo trazar e interpretar una superficie de decisión usando probabilidades predichas.
Empecemos.

Trazar una superficie de decisión para los algoritmos de aprendizaje automático en Python
Foto de Tony Webster, algunos derechos reservados.
Resumen del Tutorial
Este tutorial está dividido en tres partes; son:
- Superficie de decisión
- Conjunto de datos y modelo
- Trazar una superficie de decisión
Superficie de decisión
Los algoritmos de aprendizaje de la máquina de clasificación aprenden a asignar etiquetas a los ejemplos de entrada.
Considere las características de entrada numérica para la tarea de clasificación que define un espacio de características de entrada continua.
Podemos pensar en cada característica de entrada que define un eje o dimensión en un espacio de características. Dos características de entrada definirían un espacio de característica que es un plano, con puntos que representan coordenadas de entrada en el espacio de entrada. Si hubiera tres variables de entrada, el espacio de características sería un volumen tridimensional.
A cada punto del espacio se le puede asignar una etiqueta de clase. En términos de un espacio de características bidimensionales, podemos pensar que cada punto del plano tiene un color diferente, según su clase asignada.
El objetivo de un algoritmo de clasificación es aprender a dividir el espacio de las características de manera que las etiquetas se asignen correctamente a los puntos del espacio de las características, o al menos, tan correctamente como sea posible.
Se trata de una comprensión geométrica útil de la modelización predictiva de la clasificación. Podemos ir un paso más allá.
Una vez que el algoritmo de aprendizaje de una máquina de clasificación divide un espacio de características, podemos entonces clasificar cada punto en el espacio de características, en alguna cuadrícula arbitraria, para tener una idea de cómo exactamente el algoritmo eligió dividir el espacio de características.
Esto se llama superficie de decisión o límite de decisióny proporciona una herramienta de diagnóstico para comprender un modelo en una tarea de modelado de clasificación y predicción.
Aunque la noción de un «superficie» sugiere un espacio de característica bidimensional, el método puede ser usado con espacios de característica con más de dos dimensiones, donde se crea una superficie para cada par de características de entrada.
Ahora que estamos familiarizados con lo que es una superficie de decisión, a continuación, vamos a definir un conjunto de datos y un modelo para que más tarde exploremos la superficie de decisión.
Conjunto de datos y modelo
En esta sección, definiremos una tarea de clasificación y un modelo de predicción para aprender la tarea.
Conjunto de datos de clasificación sintética
Podemos usar la función make_blobs() scikit-learn para definir una tarea de clasificación con un espacio de características numéricas de clase bidimensional y a cada punto se le asigna una de dos etiquetas de clase, por ejemplo, una tarea de clasificación binaria.
|
... # Generar conjunto de datos X, y = make_blobs(n_muestras=1000, centros=2, n_funciones=2, estado_aleatorio=1, cluster_std=3) |
Una vez definido, podemos crear una gráfica de dispersión del espacio de los rasgos con el primer rasgo definiendo el eje x, el segundo rasgo definiendo el eje y, y cada muestra representada como un punto en el espacio de los rasgos.
Podemos colorear los puntos en el gráfico de dispersión de acuerdo con su etiqueta de clase como 0 o 1.
|
... # Crear un gráfico de dispersión para las muestras de cada clase para class_value en rango(2): # Obtener índices de fila para las muestras con esta clase row_ix = donde(y == class_value) # crear la dispersión de estas muestras pyplot.Dispersión(X[[row_ix, 0], X[[row_ix, 1]) # mostrar la trama pyplot.mostrar() |
Enlazando todo esto, el ejemplo completo de la definición y el trazado de un conjunto de datos de clasificación sintética se enumera a continuación.
|
# Generar un conjunto de datos de clasificación binaria y trazar de numpy importación donde de matplotlib importación pyplot de sklearn.conjuntos de datos importación hacer_glóbulos # Generar conjunto de datos X, y = make_blobs(n_muestras=1000, centros=2, n_funciones=2, estado_aleatorio=1, cluster_std=3) # Crear un gráfico de dispersión para las muestras de cada clase para class_value en rango(2): # Obtener índices de fila para las muestras con esta clase row_ix = donde(y == class_value) # crear la dispersión de estas muestras pyplot.Dispersión(X[[row_ix, 0], X[[row_ix, 1]) # mostrar la trama pyplot.mostrar() |
Al ejecutar el ejemplo se crea el conjunto de datos, y luego se traza el conjunto de datos como un gráfico de dispersión con puntos coloreados por la etiqueta de la clase.
Podemos ver una clara separación entre los ejemplos de las dos clases y podemos imaginarnos cómo un modelo de aprendizaje por máquina podría dibujar una línea para separar las dos clases, por ejemplo, tal vez una línea diagonal justo en el medio de los dos grupos.
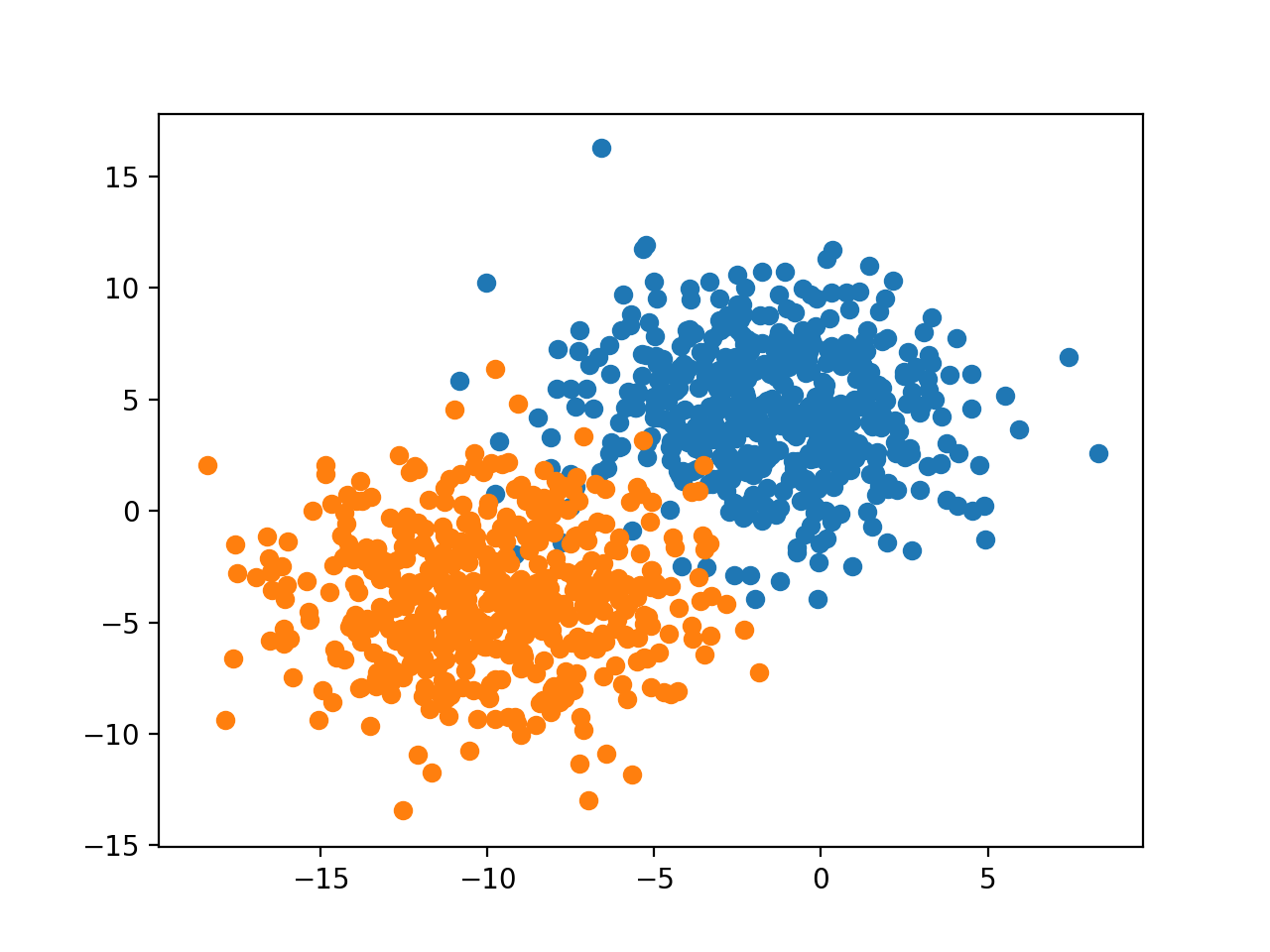
Gráfica de dispersión del conjunto de datos de clasificación binaria con espacio de características 2D
Modelo predictivo de clasificación de ajuste
Ahora podemos ajustar un modelo en nuestro conjunto de datos.
En este caso, ajustaremos un algoritmo de regresión logística porque podemos predecir tanto las etiquetas de clase como las probabilidades, que podemos utilizar en nuestra superficie de decisión.
Podemos definir el modelo, y luego ajustarlo en el conjunto de datos de entrenamiento.
|
... # Definir el modelo modelo = LogisticRegression() # Encaja con el modelo modelo.encajar(X, y) |
Una vez definido, podemos utilizar el modelo para hacer una predicción para el conjunto de datos de entrenamiento para tener una idea de lo bien que aprendió a dividir el espacio de características del conjunto de datos de entrenamiento y asignar etiquetas.
|
... # Hacer predicciones yhat = modelo.predecir(X) |
Las predicciones pueden evaluarse utilizando la precisión de la clasificación.
|
... # Evaluar las predicciones acc = accuracy_score(y, yhat) imprimir(Precisión: %.3f’. % acc) |
A continuación se presenta el ejemplo completo de ajuste y evaluación de un modelo en el conjunto de datos de la clasificación binaria sintética.
|
# Ejemplo de ajuste y evaluación de un modelo en el conjunto de datos de clasificación de sklearn.conjuntos de datos importación make_blobs de sklearn.modelo_lineal importación LogisticRegression de sklearn.métrica importación exactitud_puntuación # Generar conjunto de datos X, y = make_blobs(n_muestras=1000, centros=2, n_funciones=2, estado_aleatorio=1, cluster_std=3) # Definir el modelo modelo = LogisticRegression() # Encaja con el modelo modelo.encajar(X, y) # Hacer predicciones yhat = modelo.predecir(X) # Evaluar las predicciones acc = accuracy_score(y, yhat) imprimir(Precisión: %.3f’. % acc) |
La ejecución del ejemplo se ajusta al modelo y hace una predicción para cada ejemplo.
Sus resultados específicos pueden variar dada la naturaleza estocástica del algoritmo de aprendizaje. Intente ejecutar el ejemplo unas cuantas veces.
En este caso, podemos ver que el modelo alcanzó un rendimiento de alrededor del 97,2 por ciento.
Ahora que tenemos un conjunto de datos y un modelo, exploremos cómo podemos desarrollar una superficie de decisión.
Trazar una superficie de decisión
Podemos crear una superficie de decisión ajustando un modelo en el conjunto de datos de entrenamiento, y luego usando el modelo para hacer predicciones para una cuadrícula de valores a través del dominio de entrada.
Una vez que tengamos la cuadrícula de predicciones, podemos trazar los valores y su etiqueta de clase.
Se podría usar un gráfico de dispersión si se tomara una cuadrícula lo suficientemente fina. Un mejor enfoque es usar un gráfico de contorno que pueda interpolar los colores entre los puntos.
Se puede utilizar la función contourf() Matplotlib.
Esto requiere unos pocos pasos.
Primero, necesitamos definir una cuadrícula de puntos a través del espacio de las características.
Para ello, podemos encontrar los valores mínimos y máximos de cada rasgo y expandir la cuadrícula un paso más allá para asegurar que se cubra todo el espacio del rasgo.
|
... # Definir los límites del dominio min1, max1 = X[[:, 0].min()–1, X[[:, 0].max()+1 min2, max2 = X[[:, 1].min()–1, X[[:, 1].max()+1 |
Podemos entonces crear una muestra uniforme a través de cada dimensión usando la función arange() a una resolución elegida. Usaremos una resolución de 0,1 en este caso.
|
... # Definir la escala x y y x1grid = arange(min1, max1, 0.1) x2grid = arange(min2, max2, 0.1) |
Ahora tenemos que convertir esto en una red.
Podemos usar la función meshgrid() NumPy para crear una cuadrícula a partir de estos dos vectores.
Si el primer rasgo x1 es nuestro eje x del espacio del rasgo, entonces necesitamos una fila de valores x1 de la cuadrícula para cada punto del eje y.
De manera similar, si tomamos x2 como nuestro eje y del espacio de características, entonces necesitamos una columna de valores de x2 de la cuadrícula para cada punto del eje x.
El meshgrid() hará esto por nosotros, duplicando las filas y columnas para nosotros según sea necesario. Devuelve dos cuadrículas para los dos vectores de entrada. La primera cuadrícula de los valores x y la segunda de los valores y, organizada en una cuadrícula de tamaño apropiado de filas y columnas a través del espacio de la función.
|
... # crear todas las líneas y filas de la red xx, yy = meshgrid(x1grid, x2grid) |
Luego necesitamos aplanar la red para crear muestras que podamos introducir en el modelo y hacer una predicción.
Para ello, primero, aplanamos cada cuadrícula en un vector.
|
... # aplanar cada cuadrícula a un vector r1, r2 = xx.aplanar(), yy.aplanar() r1, r2 = r1.remodelar((len(r1), 1)), r2.remodelar((len(r2), 1)) |
Luego apilamos los vectores uno al lado del otro como columnas en un conjunto de datos de entrada, por ejemplo, como nuestro conjunto de datos de entrenamiento original, pero a una resolución mucho mayor.
|
... # Vectores de pila horizontal para crear una entrada de x1,x2 para el modelo cuadrícula = hstack((r1,r2)) |
Podemos entonces introducir esto en nuestro modelo y obtener una predicción para cada punto de la red.
|
... # Hacer predicciones para la red yhat = modelo.predecir(cuadrícula) # remodelar las predicciones de nuevo en una cuadrícula |
Hasta ahora, todo bien.
Tenemos una cuadrícula de valores a través del espacio de las características y las etiquetas de las clases, como predijo nuestro modelo.
A continuación, tenemos que trazar la cuadrícula de valores como un gráfico de contorno.
La función contourf() toma cuadrículas separadas para cada eje, al igual que lo que fue devuelto de nuestra anterior llamada a meshgrid(). ¡Grandioso!
Así que podemos usar xx y yy que preparamos antes y simplemente reformar las predicciones (yhat) del modelo para tener la misma forma.
|
... # remodelar las predicciones de nuevo en una cuadrícula zz = yhat.remodelar(xx.forma) |
Luego trazamos la superficie de decisión con un mapa de color de dos colores.
|
... # trazar la cuadrícula de los valores de x, y y z como una superficie pyplot.contourf(xx, yy, zz, cmap=«Emparejado) |
Podemos entonces trazar los puntos reales del conjunto de datos en la parte superior para ver qué tan bien fueron separados por la superficie de decisión de regresión logística.
El ejemplo completo de trazar una superficie de decisión para un modelo de regresión logística en nuestro conjunto de datos de clasificación binaria sintética se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
# Superficie de decisión para la regresión logística en un conjunto de datos de clasificación binaria de numpy importación donde de numpy importación meshgrid de numpy importación arange de numpy importación hstack de sklearn.conjuntos de datos importación make_blobs de sklearn.modelo_lineal importación LogisticRegression de matplotlib importación pyplot # Generar conjunto de datos X, y = make_blobs(n_muestras=1000, centros=2, n_funciones=2, estado_aleatorio=1, cluster_std=3) # Definir los límites del dominio min1, max1 = X[[:, 0].min()–1, X[[:, 0].max()+1 min2, max2 = X[[:, 1].min()–1, X[[:, 1].max()+1 # Definir la escala x y y x1grid = arange(min1, max1, 0.1) x2grid = arange(min2, max2, 0.1) # crear todas las líneas y filas de la red xx, yy = meshgrid(x1grid, x2grid) # aplanar cada cuadrícula a un vector r1, r2 = xx.aplanar(), yy.aplanar() r1, r2 = r1.remodelar((len(r1), 1)), r2.remodelar((len(r2), 1)) # Vectores de pila horizontal para crear una entrada de x1,x2 para el modelo cuadrícula = hstack((r1,r2)) # Definir el modelo modelo = LogisticRegression() # Encaja con el modelo modelo.encajar(X, y) # Hacer predicciones para la red yhat = modelo.predecir(cuadrícula) # remodelar las predicciones de nuevo en una cuadrícula zz = yhat.remodelar(xx.forma) # trazar la cuadrícula de los valores de x, y y z como una superficie pyplot.contourf(xx, yy, zz, cmap=«Emparejado) # Crear un gráfico de dispersión para las muestras de cada clase para class_value en rango(2): # Obtener índices de fila para las muestras con esta clase row_ix = donde(y == class_value) # crear la dispersión de estas muestras pyplot.Dispersión(X[[row_ix, 0], X[[row_ix, 1], cmap=«Emparejado) # mostrar la trama pyplot.mostrar() |
La ejecución del ejemplo se ajusta al modelo y lo utiliza para predecir los resultados de la cuadrícula de valores a través del espacio de las características y traza el resultado como un gráfico de contorno.
Podemos ver, como podríamos haber sospechado, que la regresión logística divide el espacio de las características usando una línea recta. Es un modelo lineal, después de todo; esto es todo lo que puede hacer.
Crear una superficie de decisión es casi como magia. Da una visión inmediata y significativa de cómo el modelo ha aprendido la tarea.
Inténtalo con diferentes algoritmos, como un SVM o un árbol de decisiones.
¡Ponga los mapas resultantes como enlaces en los comentarios de abajo!
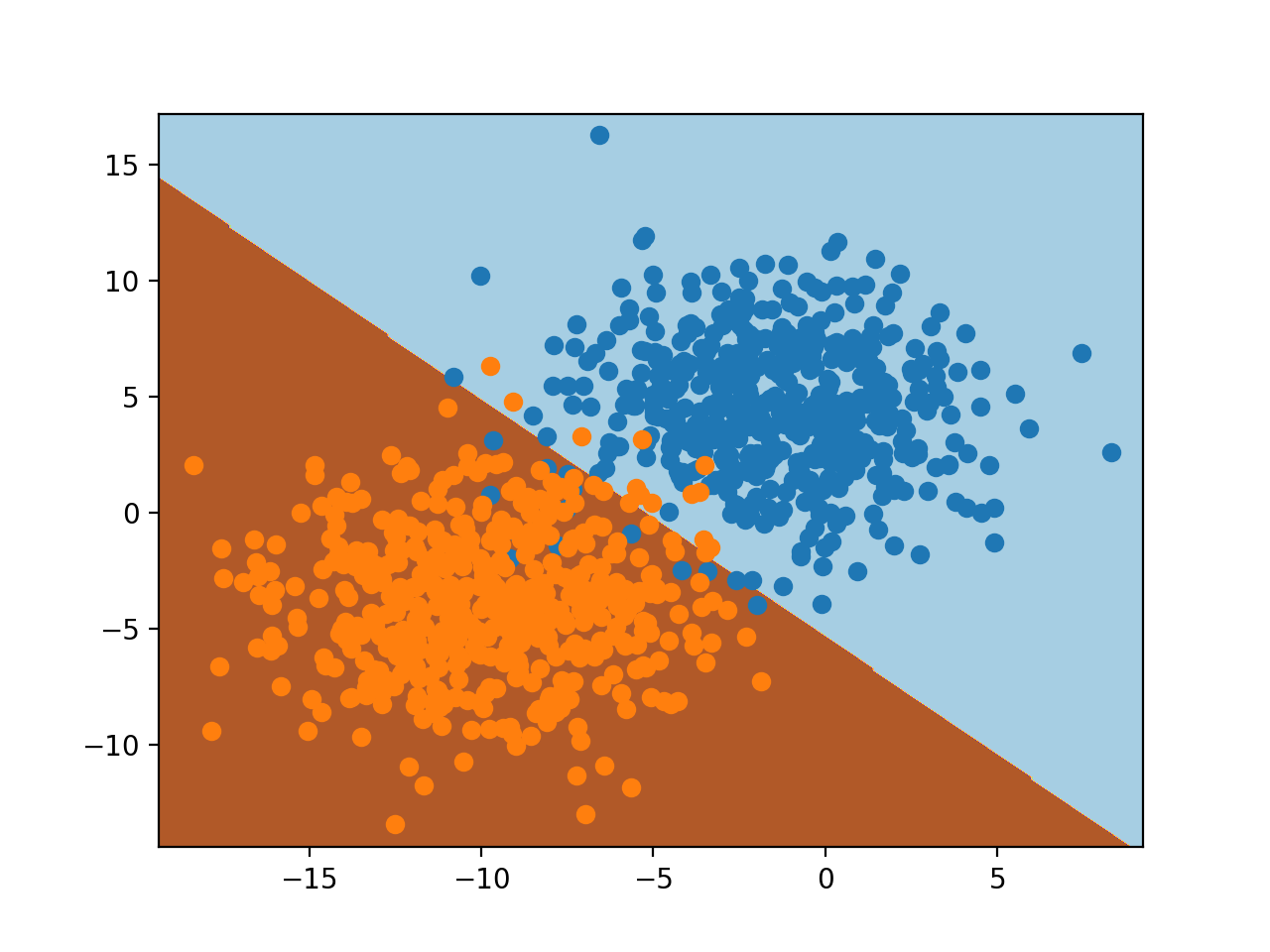
Superficie de decisión para la regresión logística en una tarea de clasificación binaria
Podemos añadir más profundidad a la superficie de decisión usando el modelo para predecir probabilidades en lugar de etiquetas de clase.
|
... # Hacer predicciones para la red yhat = modelo.predict_proba(cuadrícula) # mantener sólo las probabilidades para la clase 0 yhat = yhat[[:, 0] |
Cuando se traza, podemos ver cuán seguro o probable es que cada punto en el espacio del rasgo pertenezca a cada una de las etiquetas de la clase, según lo visto por el modelo.
Podemos usar un mapa de color diferente que tiene gradaciones, y mostrar una leyenda para poder interpretar los colores.
|
... # trazar la cuadrícula de los valores de x, y y z como una superficie c = pyplot.contourf(xx, yy, zz, cmap=«RdBu) # Añade una leyenda, llamada barra de color pyplot.colorbar(c) |
El ejemplo completo de la creación de una superficie de decisión utilizando probabilidades se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 |
# Superficie de decisión de probabilidad para la regresión logística en un conjunto de datos de clasificación binaria de numpy importación donde de numpy importación meshgrid de numpy importación arange de numpy importación hstack de sklearn.conjuntos de datos importación make_blobs de sklearn.modelo_lineal importación LogisticRegression de matplotlib importación pyplot # Generar conjunto de datos X, y = make_blobs(n_muestras=1000, centros=2, n_funciones=2, estado_aleatorio=1, cluster_std=3) # Definir los límites del dominio min1, max1 = X[[:, 0].min()–1, X[[:, 0].max()+1 min2, max2 = X[[:, 1].min()–1, X[[:, 1].max()+1 # Definir la escala x y y x1grid = arange(min1, max1, 0.1) x2grid = arange(min2, max2, 0.1) # crear todas las líneas y filas de la red xx, yy = meshgrid(x1grid, x2grid) # aplanar cada cuadrícula a un vector r1, r2 = xx.aplanar(), yy.aplanar() r1, r2 = r1.remodelar((len(r1), 1)), r2.remodelar((len(r2), 1)) # Vectores de pila horizontal para crear una entrada de x1,x2 para el modelo cuadrícula = hstack((r1,r2)) # Definir el modelo modelo = LogisticRegression() # Encaja con el modelo modelo.encajar(X, y) # Hacer predicciones para la red yhat = modelo.predict_proba(cuadrícula) # mantener sólo las probabilidades para la clase 0 yhat = yhat[[:, 0] # remodelar las predicciones de nuevo en una cuadrícula zz = yhat.remodelar(xx.forma) # trazar la cuadrícula de los valores de x, y y z como una superficie c = pyplot.contourf(xx, yy, zz, cmap=«RdBu) # Añade una leyenda, llamada barra de color pyplot.colorbar(c) # Crear un gráfico de dispersión para las muestras de cada clase para class_value en rango(2): # Obtener índices de fila para las muestras con esta clase row_ix = donde(y == class_value) # crear la dispersión de estas muestras pyplot.Dispersión(X[[row_ix, 0], X[[row_ix, 1], cmap=«Emparejado) # mostrar la trama pyplot.mostrar() |
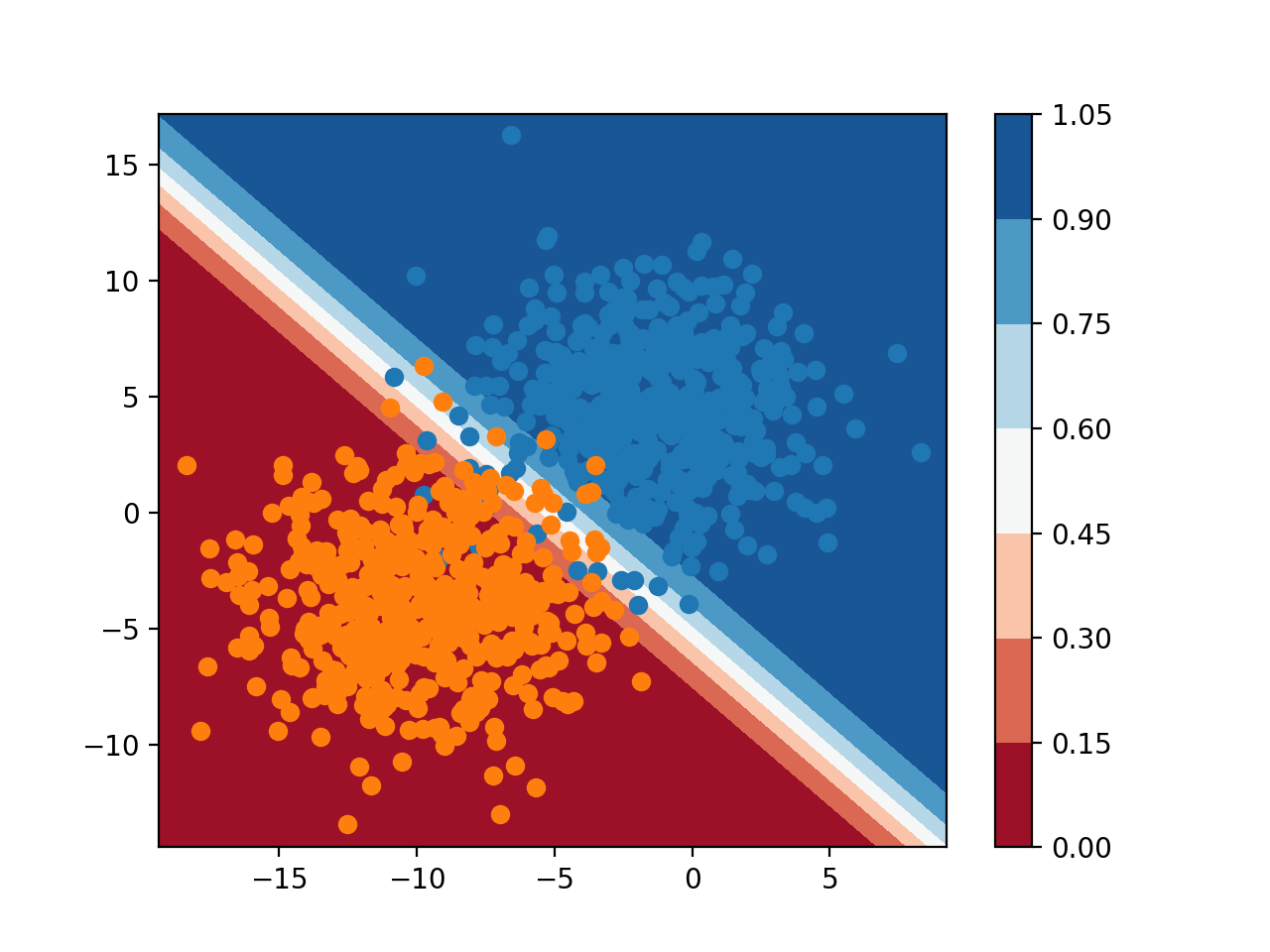
La ejecución del ejemplo predice la probabilidad de pertenencia a una clase para cada punto de la cuadrícula a través del espacio de la característica y traza el resultado.
Aquí, podemos ver que el modelo es inseguro (colores más claros) alrededor del medio del dominio, dado el ruido de muestreo en esa área del espacio de características. También podemos ver que el modelo es muy seguro (colores completos) en las mitades inferior izquierda y superior derecha del dominio.
Juntas, las nítidas superficies de decisión de clase y probabilidad son poderosas herramientas de diagnóstico para comprender su modelo y cómo divide el espacio de características para su tarea de modelado predictivo.

Superficie de decisión de probabilidad para la regresión logística en una tarea de clasificación binaria
