Regresión logística multinomial es una extensión de la regresión logística que agrega soporte nativo para problemas de clasificación de clases múltiples.
La regresión logística, por defecto, se limita a problemas de clasificación de dos clases. Algunas extensiones como uno contra resto pueden permitir el uso de regresión logística para problemas de clasificación de clases múltiples, aunque requieren que el problema de clasificación primero se transforme en problemas de clasificación binaria múltiple.
En cambio, el algoritmo de regresión logística multinomial es una extensión del modelo de regresión logística que implica cambiar la función de pérdida a pérdida de entropía cruzada y predecir la distribución de probabilidad a una distribución de probabilidad multinomial para soportar de forma nativa problemas de clasificación de clases múltiples.
En este tutorial, descubrirá cómo desarrollar modelos de regresión logística multinomial en Python.
Después de completar este tutorial, sabrá:
- La regresión logística multinomial es una extensión de la regresión logística para la clasificación de clases múltiples.
- Cómo desarrollar y evaluar la regresión logística multinomial y desarrollar un modelo final para hacer predicciones sobre nuevos datos.
- Cómo ajustar el hiperparámetro de penalización para el modelo de regresión logística multinomial.
Empecemos.
Regresión logística multinomial con Python
Foto de Nicolas Rénac, algunos derechos reservados.
Descripción general del tutorial
Este tutorial se divide en tres partes; son:
- Regresión logística multinomial
- Evaluar el modelo de regresión logística multinomial
- Tune Penalty for Multinomial Logistic Regression
Regresión logística multinomial
La regresión logística es un algoritmo de clasificación.
Está destinado a conjuntos de datos que tienen variables de entrada numéricas y una variable de destino categórica que tiene dos valores o clases. Los problemas de este tipo se denominan problemas de clasificación binaria.
La regresión logística está diseñada para problemas de dos clases, modelando el objetivo utilizando una función de distribución de probabilidad binomial. Las etiquetas de clase se asignan a 1 para la clase o resultado positivo y 0 para la clase o resultado negativo. El modelo de ajuste predice la probabilidad de que un ejemplo pertenezca a la clase 1.
De forma predeterminada, la regresión logística no se puede utilizar para tareas de clasificación que tienen más de dos etiquetas de clase, la denominada clasificación de clases múltiples.
En cambio, requiere modificaciones para admitir problemas de clasificación de clases múltiples.
Un enfoque popular para adaptar la regresión logística a problemas de clasificación de clases múltiples es dividir el problema de clasificación de clases múltiples en problemas de clasificación binaria múltiples y ajustar un modelo de regresión logística estándar en cada subproblema. Las técnicas de este tipo incluyen modelos de envoltura uno contra reposo y uno contra uno.
Un enfoque alternativo implica cambiar el modelo de regresión logística para respaldar la predicción de etiquetas de clases múltiples directamente. Específicamente, para predecir la probabilidad de que un ejemplo de entrada pertenezca a cada etiqueta de clase conocida.
La distribución de probabilidad que define las probabilidades de clases múltiples se denomina distribución de probabilidad multinomial. Un modelo de regresión logística que se adapta para aprender y predecir una distribución de probabilidad multinomial se denomina Regresión logística multinomial. De manera similar, podríamos referirnos a la regresión logística estándar o predeterminada como Regresión logística binomial.
- Regresión logística binomial: Regresión logística estándar que predice una probabilidad binomial (es decir, para dos clases) para cada ejemplo de entrada.
- Regresión logística multinomial: Versión modificada de la regresión logística que predice una probabilidad multinomial (es decir, más de dos clases) para cada ejemplo de entrada.
Si es nuevo en las distribuciones de probabilidad binomial y multinomial, es posible que desee leer el tutorial:
Cambiar la regresión logística de probabilidad binomial a multinomial requiere un cambio en la función de pérdida utilizada para entrenar el modelo (por ejemplo, pérdida de registro a pérdida de entropía cruzada) y un cambio en la salida de un valor de probabilidad único a una probabilidad para cada etiqueta de clase.
Ahora que estamos familiarizados con la regresión logística multinomial, veamos cómo podemos desarrollar y evaluar modelos de regresión logística multinomial en Python.
Evaluar el modelo de regresión logística multinomial
En esta sección, desarrollaremos y evaluaremos un modelo de regresión logística multinomial utilizando la biblioteca de aprendizaje automático de Python scikit-learn.
Primero, definiremos un conjunto de datos sintéticos de clasificación de clases múltiples para usar como base de la investigación. Este es un conjunto de datos genérico que puede reemplazar fácilmente con su propio conjunto de datos cargado más adelante.
La función make_classification () se puede utilizar para generar un conjunto de datos con un número determinado de filas, columnas y clases. En este caso, generaremos un conjunto de datos con 1000 filas, 10 variables de entrada o columnas y 3 clases.
El siguiente ejemplo genera el conjunto de datos y resume la forma de las matrices y la distribución de ejemplos en las tres clases.
|
# conjunto de datos de clasificación de prueba desde colecciones importar Mostrador desde sklearn.conjuntos de datos importar hacer_clasificación # definir conjunto de datos X, y = make_classification(n_samples=1000, n_features=10, n_informativo=5, n_redundante=5, n_clases=3, estado_aleatorio=1) # resumir el conjunto de datos impresión(X.forma, y.forma) impresión(Mostrador(y)) |
La ejecución del ejemplo confirma que el conjunto de datos tiene 1000 filas y 10 columnas, como esperábamos, y que las filas se distribuyen aproximadamente de manera uniforme en las tres clases, con aproximadamente 334 ejemplos en cada clase.
|
(1000, 10) (1000,) Contador ({1: 334, 2: 334, 0: 332}) |
La regresión logística se admite en la biblioteca scikit-learn a través de la clase LogisticRegression.
los Regresión logística La clase se puede configurar para la regresión logística multinomial estableciendo el «multi_clase«Argumento a»multinomial» y el «solucionador«Argumento a un solucionador que admita la regresión logística multinomial, como»lbfgs“.
|
... # definir el modelo de regresión logística multinomial modelo = Regresión logística(multi_clase=‘multinomial’, solucionador=‘lbfgs’) |
El modelo de regresión logística multinomial se ajustará mediante la pérdida de entropía cruzada y predecirá el valor entero para cada etiqueta de clase codificada como entero.
Ahora que estamos familiarizados con la API de regresión logística multinomial, podemos ver cómo podemos evaluar un modelo de regresión logística multinomial en nuestro conjunto de datos sintéticos de clasificación de clases múltiples.
Es una buena práctica evaluar los modelos de clasificación utilizando una validación cruzada de k-veces estratificada repetida. La estratificación asegura que cada pliegue de validación cruzada tenga aproximadamente la misma distribución de ejemplos en cada clase que el conjunto de datos de entrenamiento completo.
Usaremos tres repeticiones con 10 pliegues, lo cual es un buen valor predeterminado, y evaluaremos el desempeño del modelo usando precisión de clasificación dado que las clases están balanceadas.
El ejemplo completo de evaluación de la regresión logística multinomial para la clasificación de clases múltiples se muestra a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 |
# evaluar el modelo de regresión logística multinomial desde numpy importar media desde numpy importar std desde sklearn.conjuntos de datos importar make_classification desde sklearn.model_selection importar cross_val_score desde sklearn.model_selection importar Repetido estratificado KFold desde sklearn.Modelo lineal importar Regresión logística # definir conjunto de datos X, y = make_classification(n_samples=1000, n_features=10, n_informativo=5, n_redundante=5, n_clases=3, estado_aleatorio=1) # definir el modelo de regresión logística multinomial modelo = Regresión logística(multi_clase=‘multinomial’, solucionador=‘lbfgs’) # definir el procedimiento de evaluación del modelo CV = Repetido estratificado KFold(n_splits=10, n_repeats=3, estado_aleatorio=1) # evaluar el modelo y recopilar las puntuaciones n_scores = cross_val_score(modelo, X, y, puntuación=‘exactitud’, CV=CV, n_jobs=–1) # informar el rendimiento del modelo impresión(‘Precisión media:% .3f (% .3f)’ % (media(n_scores), std(n_scores))) |
La ejecución del ejemplo informa la precisión de clasificación media en todos los pliegues y repeticiones del procedimiento de evaluación.
Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o procedimiento de evaluación, o las diferencias en la precisión numérica. Considere ejecutar el ejemplo varias veces y compare el resultado promedio.
En este caso, podemos ver que el modelo de regresión logística multinomial con penalización por defecto logró una precisión de clasificación media de alrededor del 68,1 por ciento en nuestro conjunto de datos de clasificación sintética.
|
Precisión media: 0,681 (0,042) |
Podemos decidir utilizar el modelo de regresión logística multinomial como nuestro modelo final y hacer predicciones sobre nuevos datos.
Esto se puede lograr ajustando primero el modelo a todos los datos disponibles, luego llamando al predecir() función para hacer una predicción de nuevos datos.
El siguiente ejemplo demuestra cómo hacer una predicción para nuevos datos utilizando el modelo de regresión logística multinomial.
|
# hacer una predicción con un modelo de regresión logística multinomial desde sklearn.conjuntos de datos importar make_classification desde sklearn.Modelo lineal importar Regresión logística # definir conjunto de datos X, y = make_classification(n_samples=1000, n_features=10, n_informativo=5, n_redundante=5, n_clases=3, estado_aleatorio=1) # definir el modelo de regresión logística multinomial modelo = Regresión logística(multi_clase=‘multinomial’, solucionador=‘lbfgs’) # ajustar el modelo en todo el conjunto de datos modelo.ajuste(X, y) # definir una sola fila de datos de entrada fila = [[1.89149379, –0.39847585, 1.63856893, 0.01647165, 1.51892395, –3.52651223, 1,80998823, 0.58810926, –0.02542177, –0.52835426] # predecir la etiqueta de la clase yhat = modelo.predecir([[fila]) # resumir la clase predicha impresión(‘Clase prevista:% d’ % yhat[[0]) |
Al ejecutar el ejemplo, primero se ajusta el modelo a todos los datos disponibles, luego se define una fila de datos, que se proporciona al modelo para realizar una predicción.
En este caso, podemos ver que el modelo predijo la clase «1» para la única fila de datos.
Un beneficio de la regresión logística multinomial es que puede predecir probabilidades calibradas en todas las etiquetas de clase conocidas en el conjunto de datos.
Esto se puede lograr llamando al predecir_proba () función en el modelo.
El siguiente ejemplo demuestra cómo predecir una distribución de probabilidad multinomial para un nuevo ejemplo utilizando el modelo de regresión logística multinomial.
|
# predecir probabilidades con un modelo de regresión logística multinomial desde sklearn.conjuntos de datos importar make_classification desde sklearn.Modelo lineal importar Regresión logística # definir conjunto de datos X, y = make_classification(n_samples=1000, n_features=10, n_informativo=5, n_redundante=5, n_clases=3, estado_aleatorio=1) # definir el modelo de regresión logística multinomial modelo = Regresión logística(multi_clase=‘multinomial’, solucionador=‘lbfgs’) # ajustar el modelo en todo el conjunto de datos modelo.ajuste(X, y) # definir una sola fila de datos de entrada fila = [[1.89149379, –0.39847585, 1.63856893, 0.01647165, 1.51892395, –3.52651223, 1,80998823, 0.58810926, –0.02542177, –0.52835426] # predecir una distribución de probabilidad multinomial yhat = modelo.predecir_proba([[fila]) # resumir las probabilidades predichas impresión(‘Probabilidades previstas:% s’ % yhat[[0]) |
Al ejecutar el ejemplo, primero se ajusta el modelo a todos los datos disponibles, luego se define una fila de datos, que se proporciona al modelo para predecir las probabilidades de clase.
Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o procedimiento de evaluación, o las diferencias en la precisión numérica. Considere ejecutar el ejemplo varias veces y compare el resultado promedio.
En este caso, podemos ver que la clase 1 (por ejemplo, el índice de la matriz se asigna al valor entero de la clase) tiene la mayor probabilidad predicha con aproximadamente 0,50.
|
Probabilidades pronosticadas: [0.16470456 0.50297138 0.33232406] |
Ahora que estamos familiarizados con la evaluación y el uso de modelos de regresión logística multinomial, exploremos cómo podemos ajustar los hiperparámetros del modelo.
Tune Penalty for Multinomial Logistic Regression
Un hiperparámetro importante para ajustar para la regresión logística multinomial es el término de penalización.
Este término impone presión sobre el modelo para buscar pesos de modelo más pequeños. Esto se logra agregando una suma ponderada de los coeficientes del modelo a la función de pérdida, alentando al modelo a reducir el tamaño de los pesos junto con el error mientras ajusta el modelo.
Un tipo popular de penalización es la penalización L2 que suma la suma (ponderada) de los coeficientes al cuadrado a la función de pérdida. Se puede usar una ponderación de los coeficientes que reduce la fuerza de la penalización de una penalización completa a una penalización muy leve.
Por defecto, el Regresión logística La clase usa la penalización L2 con una ponderación de coeficientes establecida en 1.0. El tipo de penalización se puede establecer mediante el «multa«Argumento con valores de»l1«,»l2«,»red elástica”(Por ejemplo, ambos), aunque no todos los solucionadores admiten todos los tipos de penalización. La ponderación de los coeficientes en la penalización se puede establecer mediante el «C» argumento.
|
... # definir el modelo de regresión logística multinomial con una penalización predeterminada Regresión logística(multi_clase=‘multinomial’, solucionador=‘lbfgs’, multa=‘l2’, C=1.0) |
La ponderación de la penalización es en realidad la ponderación inversa, quizás penalización = 1 – C.
De la documentación:
C: flotante, predeterminado = 1.0
Inversa de la fuerza de regularización; debe ser un flotador positivo. Como en las máquinas de vectores de soporte, los valores más pequeños especifican una regularización más fuerte.
Esto significa que los valores cercanos a 1.0 indican muy poca penalización y los valores cercanos a cero indican una fuerte penalización. Un valor C de 1.0 puede indicar que no hay penalización en absoluto.
- C cerca de 1.0: Penalización leve.
- C cerca de 0.0: Fuerte penalización.
La penalización puede desactivarse configurando el «multa«Argumento de la cadena»ninguna“.
|
... # definir el modelo de regresión logística multinomial sin penalización Regresión logística(multi_clase=‘multinomial’, solucionador=‘lbfgs’, multa=‘ninguna’) |
Ahora que estamos familiarizados con la penalización, veamos cómo podríamos explorar el efecto de diferentes valores de penalización en el desempeño del modelo de regresión logística multinomial.
Es común probar los valores de penalización en una escala logarítmica para descubrir rápidamente la escala de penalización que funciona bien para un modelo. Una vez encontrado, un mayor ajuste a esa escala puede ser beneficioso.
Exploraremos la penalización L2 con valores de ponderación en el rango de 0.0001 a 1.0 en una escala logarítmica, además de sin penalización o 0.0.
El ejemplo completo de evaluación de los valores de penalización L2 para la regresión logística multinomial se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 |
# ajustar la regularización para la regresión logística multinomial desde numpy importar media desde numpy importar std desde sklearn.conjuntos de datos importar make_classification desde sklearn.model_selection importar cross_val_score desde sklearn.model_selection importar Repetido estratificado KFold desde sklearn.Modelo lineal importar Regresión logística desde matplotlib importar pyplot # obtener el conjunto de datos def get_dataset(): X, y = make_classification(n_samples=1000, n_features=20, n_informativo=15, n_redundante=5, estado_aleatorio=1, n_clases=3) regreso X, y # obtener una lista de modelos para evaluar def get_models(): modelos = dictar() para pags en [[0.0, 0,0001, 0,001, 0,01, 0,1, 1.0]: # crear nombre para modelo llave = ‘% .4f’ % pags # desactivar la penalización en algunos casos Si pags == 0.0: # sin penalización en este caso modelos[[llave] = Regresión logística(multi_clase=‘multinomial’, solucionador=‘lbfgs’, multa=‘ninguna’) más: modelos[[llave] = Regresión logística(multi_clase=‘multinomial’, solucionador=‘lbfgs’, multa=‘l2’, C=pags) regreso modelos # evaluar un modelo dado mediante validación cruzada def evaluar_modelo(modelo, X, y): # definir el procedimiento de evaluación CV = Repetido estratificado KFold(n_splits=10, n_repeats=3, estado_aleatorio=1) # evaluar el modelo puntuaciones = cross_val_score(modelo, X, y, puntuación=‘exactitud’, CV=CV, n_jobs=–1) regreso puntuaciones # definir conjunto de datos X, y = get_dataset() # obtener los modelos para evaluar modelos = get_models() # evaluar los modelos y almacenar los resultados resultados, nombres = lista(), lista() para nombre, modelo en modelos.artículos(): # evaluar el modelo y recopilar las puntuaciones puntuaciones = evaluar_modelo(modelo, X, y) # almacenar los resultados resultados.adjuntar(puntuaciones) nombres.adjuntar(nombre) # resumir el progreso a lo largo del camino impresión(‘>% s% .3f (% .3f)’ % (nombre, media(puntuaciones), std(puntuaciones))) # trazar el rendimiento del modelo para comparar pyplot.diagrama de caja(resultados, etiquetas=nombres, mostrar significa=Cierto) pyplot.show() |
La ejecución del ejemplo informa la precisión de clasificación media para cada configuración a lo largo del camino.
Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o procedimiento de evaluación, o las diferencias en la precisión numérica. Considere ejecutar el ejemplo varias veces y compare el resultado promedio.
En este caso, podemos ver que un valor de C de 1.0 tiene la mejor puntuación de alrededor del 77,7 por ciento, que es lo mismo que usar ninguna penalización que logra la misma puntuación.
|
> 0,0000 0,777 (0,037) > 0,0001 0,683 (0,049) > 0,0010 0,762 (0,044) > 0,0100 0,775 (0,040) > 0,1000 0,774 (0,038) > 1,0000 0,777 (0,037) |
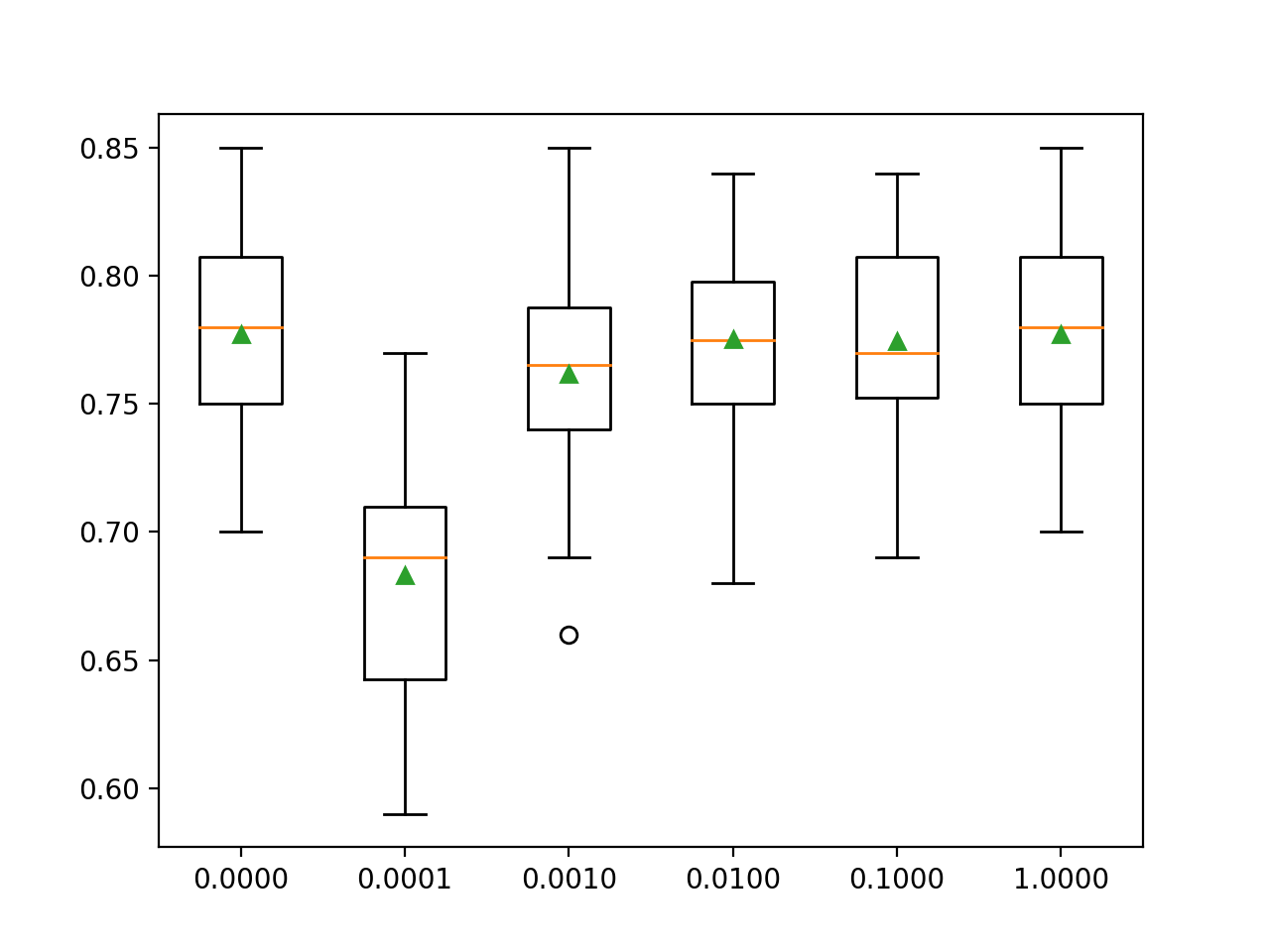
Se crea una gráfica de caja y bigotes para las puntuaciones de precisión de cada configuración y todas las gráficas se muestran una al lado de la otra en una figura en la misma escala para una comparación directa.
En este caso, podemos ver que cuanto mayor sea la penalización que usemos en este conjunto de datos (es decir, cuanto menor sea el valor de C), peor será el rendimiento del modelo.
Gráficos de caja y bigotes de la configuración de penalización L2 frente a la precisión para la regresión logística multinomial
Otras lecturas
Esta sección proporciona más recursos sobre el tema si está buscando profundizar.
Tutoriales relacionados
API
Artículos
Resumen
En este tutorial, descubrió cómo desarrollar modelos de regresión logística multinomial en Python.
Específicamente, aprendiste:
- La regresión logística multinomial es una extensión de la regresión logística para la clasificación de clases múltiples.
- Cómo desarrollar y evaluar la regresión logística multinomial y desarrollar un modelo final para hacer predicciones sobre nuevos datos.
- Cómo ajustar el hiperparámetro de penalización para el modelo de regresión logística multinomial.
¿Tiene usted alguna pregunta?
Haga sus preguntas en los comentarios a continuación y haré todo lo posible para responder.
¡Descubra el aprendizaje automático rápido en Python!
Desarrolle sus propios modelos en minutos
… con solo unas pocas líneas de código scikit-learn
Aprenda cómo en mi nuevo libro electrónico:
Dominio del aprendizaje automático con Python
Cubiertas tutoriales de autoaprendizaje y proyectos de principio a fin me gusta:
Cargando datos, visualización, modelado, Afinación, y mucho más…
Finalmente, lleve el aprendizaje automático a
Tus Propios Proyectos
Sáltese los académicos. Solo resultados.
Mira lo que hay dentro